多模GNSS卫星轨道插值方法研究

李天驰，王 果

(河南工程学院 土木工程学院，河南 郑州 451191)

精密的卫星轨道是接收机等终端设备导航定位的基础[1]，利用精密星历进行卫星位置插值计算在精密单点定位、低轨道星载GPS精密定轨等方面具有重要意义。精密星历或插值方法的选择直接影响卫星定轨精度，进而对定位产生影响[2-4]。洪樱等[5]利用GPS的精密星历分析和比较了两种滑动式多项式插值及线性插值法，得出Newton插值算法效率比Lagrange插值效率高的结论。汪威等[6]利用北斗的精密星历分析了不同插值方法对不同轨道的卫星插值误差及多项式的阶数关系，提出对BDS不同类型的卫星采用不同方法与不同阶次进行插值计算。汪平等[7]利用IGS(international GNSS service)提供的快速精密星历和事后精密星历进行卫星定位精度对比，提出二者定位精度均能达到毫米级，可用快速精密星历代替事后精密星历进行卫星定位，而且不影响定位精度。

随着BDS和GLONASS卫星的逐步完善，多卫星导航系统(Multi-GNSS，简称为多模)定位已大量应用在科研和民用领域，如在森林中定位并进行资源调查[8]、车载导航[9]、基于Android平台的智能手机实时定位[10]、精准农业中实现农机自动驾驶[11]等。袁宏超等[12]在BDS及GPS双系统的基础上研究对比了多频RTK定位算法，提出双系统联合定位精度要高于各个单系统定位精度。李湘梅等[13]基于BDS、GLONASS和GPS系统对多模式单点定位性能进行了比较分析，提出随着卫星高度截止角的增大，三系统组合模式的定位精度高于其他模式。

然而，现有研究大多关注于某一定位系统，对多系统组合定位下卫星插值方法的研究较少。因此，本研究在现有文献的基础上，利用多系统精密星历数据，在相同阶数的条件下分别使用Lagrange插值法、Neville插值法和Chebyshev多项式拟合法计算任意时刻的卫星位置，经过数据处理，分析了3种方法计算结果的精度，为计算多模GNSS卫星位置提供了参考。

1 多模GNSS卫星轨道插值方法及精度评定

1.1 Lagrange插值法

Lagrange插值法在GPS定轨计算中已被广泛应用[14]。该方法的基本原理是由已知二维观测数据构造一个多项式，再代入待插值点即可得到插值数据。

已知时间轴的n+1个节点t0,t1,t2,…，tn及其对应的卫星坐标值x0，x1,x2,…，xn,则t时刻函数值的插值公式为

(1)

式中：ti、tj为已知时间轴节点；xi为ti时刻卫星X或Y或Z方向的坐标值；n为插值阶数；xt为插值计算得到的卫星X或Y或Z方向的坐标值。

1.2 Neville插值法

Neville插值法与Newton插值法类似，都是在Lagrange插值法的基础上进行算法改进而得。Lagrange插值时，每增加一个新节点都要重新计算，即它不具备承袭性。Neville插值的基本思想是通过线性逐步求差来避免增加节点带来的计算冗余[15]。

已知时间轴上有n+1个节点x0,x1,x2,…,xn及其对应的卫星各方向坐标值f(x)0,f(x)1,f(x)2,…,f(x)n，则递推公式为

Ti,0=f(x)i，

(2)

(3)

式中：Ti,0表示第i时刻第0阶的插值结果；Ti-1, j-1表示第i-1时刻第j-1阶的插值结果；Ti, j-1表示第i时刻第j-1阶的插值结果；Ti, j表示第i时刻第j阶的插值结果。

1.3 Chebyshev多项式拟合法

多项式拟合常用Chebyshev多项式和Legendre多项式。采用Chebyshev多项式拟合法，当时间历元选取较长时段、采用高阶多项式时，拟合效果最佳，即使是时间历元两端的时间节点，其拟合效果也比较好，避免了龙格现象对实验结果的影响[16]。

假定欲将在间隔[ts,te]的卫星轨道用n阶切比雪夫多项式逼近，其中ts为开始时刻、te为结束时刻，Δt=te-ts为拟合时间区间的长度，先将变量t∈[ts,te]归化到区间τ∈[-1,1]，即

(4)

卫星在空间中任一方向坐标可用切比雪夫多项式表示为

(5)

式中：n为拟合阶数；Cxi为切比雪夫多项式系数。对MGEX提供的卫星位置数据采用最小二乘拟合法可以求出Cxi。利用递推方式，切比雪夫多项式Ti可确定为

T0(τ)=1，

(6)

T1(τ)=τ，

(7)

Tn(τ)=2τTn-1(τ)-Tn-2(τ),|τ|≤1,n≥2。

(8)

1.4 插值方法精度评定指标

对计算差值结果需要进行精度评定，常用的精度评定指标有残差、均方根误差、标准差等。为了直观地显示计算数据的精度，本研究采用残差、均方根误差及平均绝对误差作为评价指标。

1.4.1残差

残差是指实际值与计算结果之间的差值，在卫星定轨计算中，表示的是卫星位置观测数据与插值计算得到的数据之差。残差反映了插值计算得到的卫星位置数据的离散程度。一般来说，残差越小，卫星位置插值结果与观测数据越吻合，精度越高。

1.4.2均方根误差

均方根误差在卫星定轨计算中表示卫星位置观测数据与插值计算得到的数据的平方和求平均后的平方根，它能够直观地显示卫星位置插值结果与观测数据之间的偏差。均方根误差越小，计算结果精度越高。其定义为

(9)

式中：xobserve,i为第i次的观测值，即MGEX提供的卫星位置数据；xmodel,i为第i次的预测值，即使用不同插值或拟合方法计算得到的卫星位置数据；n为插值或拟合阶数。

1.4.3平均绝对误差

平均绝对误差在卫星定轨计算中表示的是残差绝对值之和再求平均，使用残差绝对值可以避免误差相互抵消的问题，能很好地反映计算结果误差的实际情况。其定义为

(10)

式中：xobserve,i为第i次的观测值，即MGEX提供的卫星位置数据；xmodel,i为第i次使用不同插值或拟合方法计算得到的卫星位置数据；n为插值或拟合阶数。

2 多模GNSS卫星轨道插值实验与分析

2.1 数据选取与实验

本次实验采用的是由欧洲定轨中心(center for orbit determination in Europe，CODE)提供的精密星历数据，随机选取2019年4月20日00：00起间隔为5 min的数据。为了能有效评估龙格现象，插值或拟合阶数选定为20阶，则相应插值节点为21个。由于本次实验选取的时间节点间隔为10 min，则总历元时长约为6 h。随机选取6：30—13：10以10 min为间隔的PG04(GPS)、PR10(GLONASS)及PC06(BDS)卫星数据，插值计算5 min间隔的卫星位置。

为了避免在插值过程中出现龙格现象[17]，本次实验的插值方法采用滑动式，即通过不断变换插值区间，使内插点始终位于数据点中央，以此来提高插值精度。对选取的数据，分别使用滑动式Lagrange插值法、Neville插值法与Chebyshev多项式拟合法进行计算，在MATLAB R2017B环境下进行编程，得到了起始历元在8：05、终止历元在11：25的21个节点的卫星位置数据。

2.2 结果及分析

2.2.1滑动式Lagrange插值法精度分析

为方便比较，选取各类卫星的5个节点(10：15—10：55)的残差，插值结果见表1，均方根误差与平均绝对误差见表2。计算结果的残差比较图像见图1。

表1 Lagrange插值结果Tab.1 The results of Lagrange interpolation

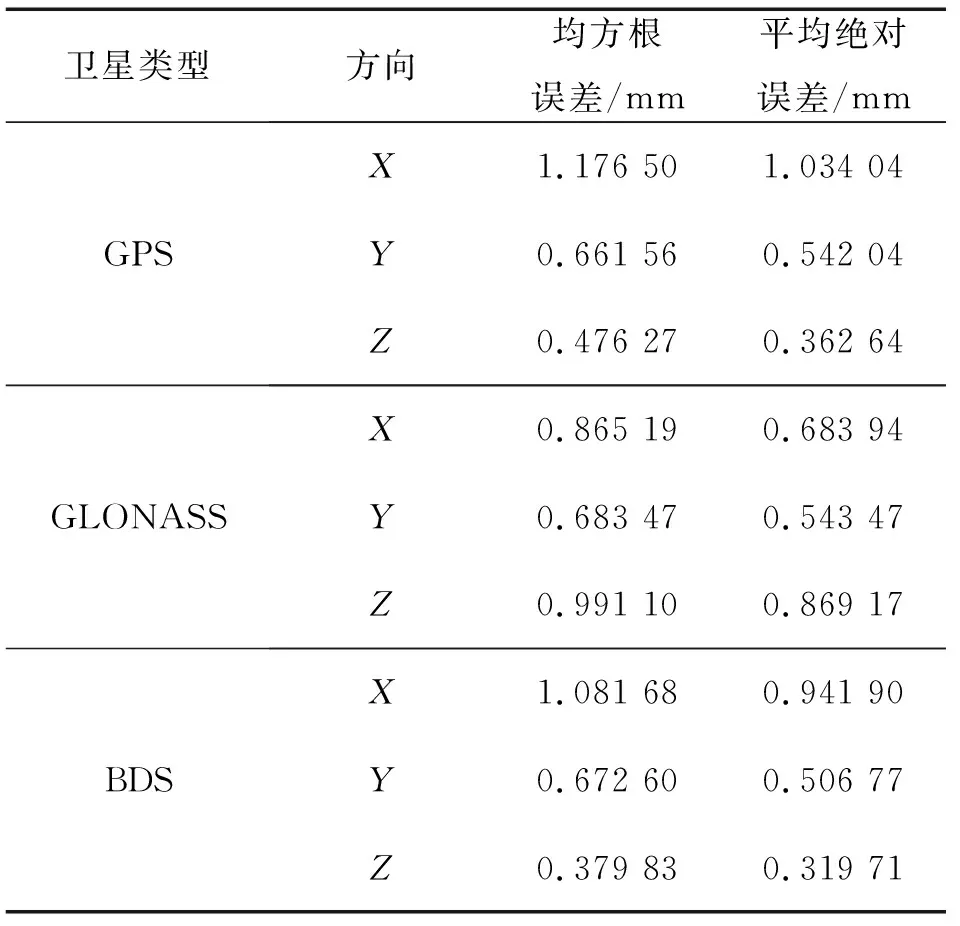
表2 Lagrange插值法计算结果精度评定Tab.2 Accuracy evaluation of Lagrange interpolation calculation results

图1 Lagrange插值法计算3类卫星位置的结果残差Fig.1 The residual error of three kinds of satellite positions calculated by Lagrange interpolation

从表1和图1可以看出，由于使用了滑动式Lagrange插值法，所以在内插点两端基本没有出现龙格现象。各类卫星计算结果的插值误差在2.5 mm内，最优处为PG04(GPS)卫星8：35、Z方向，残差达到0.004 1 mm。Lagrange插值法计算卫星X方向的位置数据误差较大，残差最大值达到-2.212 mm，而计算卫星Y或Z方向位置数据误差均较小，基本在1.5 mm以下。从表2中可以看出，Lagrange插值法计算GPS和BDS卫星位置效果较好。

2.2.2Neville插值法精度分析

Neville插值法计算结果见表3、表4和图2。表3为选取各类卫星5个节点的残差结果，表4为Neville插值精度评价，图2为3类卫星插值结果残差比较图。从表3和图2可以看出，各类卫星插值结果误差基本在2.5 mm以内，但PC06(BOS)卫星在11：25、Z方向误差达到-4.335 9 mm。最优处为PG04(GPS)卫星在9：05、Z方向，残差为0.018 8 mm。从表4可以看出，用Neville插值法计算卫星Z方向位置数据误差较大，计算GPS和GLONASS卫星位置精度较高。

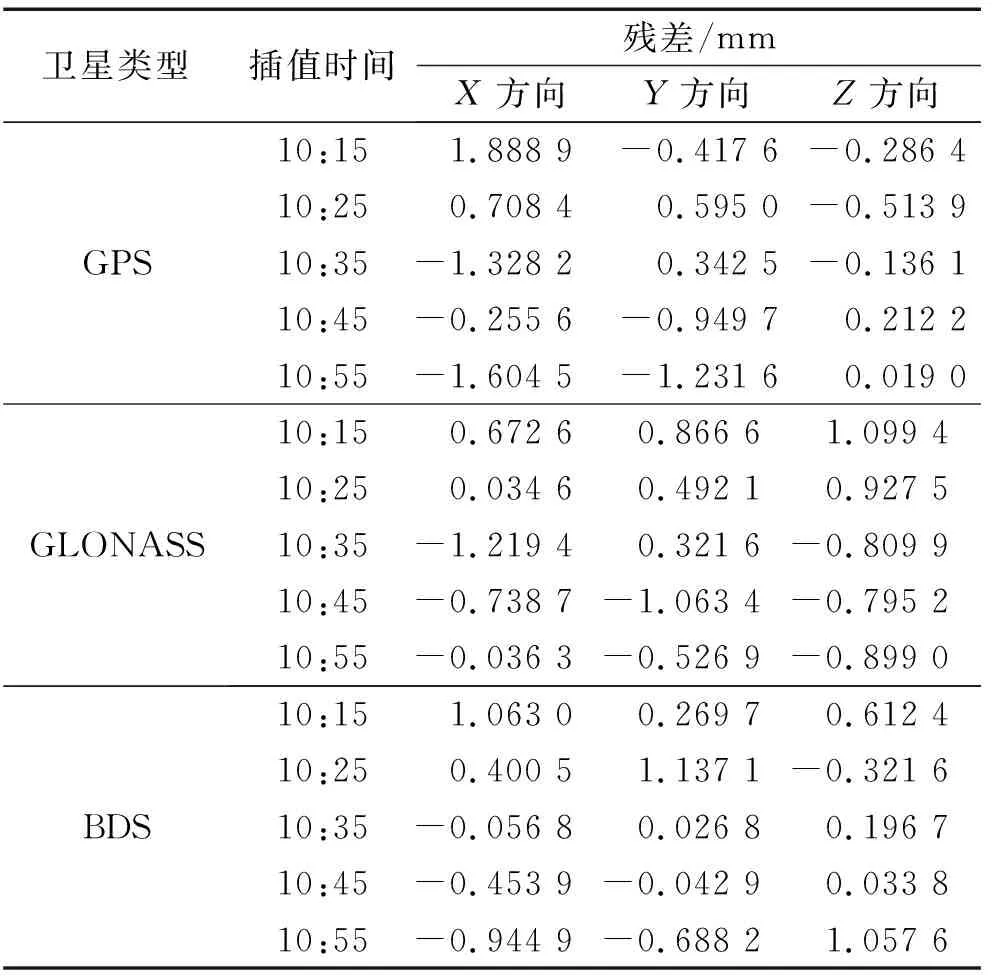
表3 Neville插值结果Tab.3 The results of Neville interpolation

表4 Neville插值法计算结果精度评定Tab.4 Accuracy evaluation of Neville interpolation calculation results

图2 Neville插值法计算3类卫星位置的结果残差Fig.2 The residual error of three kinds of satellite positions calculated by Neville interpolation

2.2.3Chebyshev多项式拟合法精度分析

Chebyshev多项式拟合法计算结果见表5、表6和图3。表5为选取各类卫星5个节点的残差结果，表6为Chebyshev拟合精度评价，图3为3类卫星插值结果残差比较图。从表5和图3可以看出，各类卫星插值结果误差基本都在2 mm以内，有些卫星甚至达到1 mm以内。最优处为PC06(BDS)卫星在11：15、Y方向，残差达到-0.000 2 mm。从表6中可以看出，用Chebyshev多项式拟合法计算BDS卫星Z方向精度最高，其均方根误差和平均绝对误差值均为最小。综合比较，用Chebyshev多项式拟合法计算GPS和BDS卫星位置精度较高。

表5 Chebyshev多项式拟合结果Tab.5 The results of Chebyshev polynomial

表6 Chebyshe多项式拟合法计算结果精度评定Tab.6 Accuracy evaluation of Chebyshe polynomial calculation results

表5(续)

表6(续)

图3 Chebyshev多项式拟合法计算3类卫星位置的结果残差Fig.3 The residual error of three kinds of satellite positions calculated by Chebyshev interpolation

3 结语

本研究采用CODE发布的精密星历数据，分别使用Lagrange插值法、Neville插值法与Chebyshev多项式拟合法对GPS、GLONASS和BDS卫星位置进行了计算。高阶插值计算容易在时间节点两端出现龙格震荡现象，本研究对传统插值算法进行改进，使用滑动式算法以减少龙格现象的影响。对计算结果进行综合比较，Lagrange插值法和Chebyshev多项式拟合法计算结果残差均在2.5 mm内，Neville插值法计算结果残差在5 mm内。对于不同方向的空间位置，3类方法计算卫星X方向的误差均较大，如Lagrange插值法计算PR10(GLONASS)卫星8：05、X方向残差为-2.212 mm。对于GPS卫星，使用3个插值方法计算效果均较好；对于BDS卫星，使用Lagrange插值法和Chebyshev多项式拟合法计算效果较好；对于GLONASS卫星，使用Neville插值法计算效果较好。在编程算法实现方面，Neville插值法通过逐步求差的方法计算插值点数据，比Lagrange插值法和Chebyshev多项式拟合法效率高。