基于神经网络的电池SOC估算及优化方法
2020-06-06李永颖张振东朱顺良
李永颖,张振东,朱顺良
(1.上海理工大学,机械工程学院,上海 200093; 2.国家机动车产品质量检测与监督中心,新能源研究所,上海 201800)
0 引言
电动汽车动力电池的电荷状态(State of Charge, SOC)、健康状态(State of Health, SOH)、峰值功率(State-of-power, SOP)、能量状态 (State of Energy,SOE)、剩余寿命(Residual Life, RUL)等参数是电池管理系统BMS(Battery Management System)对动力电池进行实时状态分析的支撑。动力电池电化学反应过程复杂,受到温度、湿度、老化等诸多因素的共同影响,具有不确定性,其数学建模涉及多学科和多领域,一直是学术界和工业界研究的难点和重点[1]。神经网络模型具有很好的非线性逼近能力,在处理非线性时变问题上具有巨大优势。蔡信等[2]利用ADVISOR仿真数据对BP神经网络进行SOC估计,结果表明模型的估计值和输出值之间的误差为4%左右。苏振浩等[3]使用经过等效电路模型修正后的数据对双隐层BP神经网络进行训练与SOC预测,证明了人工神经网络模型对SOC估算的有效性。刘征宇等[4]基于量子微粒群算法(QPSO)的BP神经网络模型用于SOC预测,结果表明此方法比现有的神经网络预测方法准确度更高,且具备很好的实用性。JOHNSONVH[5]基于ADVISOR平台建立一个双隐层神经网络的电池模型。用电池负载功率和 SOC输入到模型,输出为电流和电压。针对神经网络结构设计方法困难、模型运算时间较长、对芯片运算能力要求高等原因降低其实用性的问题。在这里提出了能有效减少模型运算时间的训练算法和基于数学规划的神经网络模型构架设计方法。为神经网络对电池状态估计的工程应用提供一个解决方案,具有参考价值。
1 前馈神经网络模型构架设计
模型深度和宽度的选择是一个非常复杂的问题,目前并没有理论的指导,没有一个好的解析式来表示。隐藏层单元数目与问题的需求、输入、输出单元数都有直接的关系。一般情况下仅能靠经验来确定模型的宽度和深度。
关于BP神经网络的隐藏层的设计有以下几种设计经验参考:
1)1987年Hechtnielsen[6]提出隐藏层节点的数目为2n+1,式中n为输入的节点数。
2)1988年Liu W[7]根据实验发现,在高维输入时,第一隐藏层对第二隐藏层的最佳节点比列为3:1。
3)1990年Nelson和Illingworth[8]建议隐藏层节点数应为4n。
4)隐含层的的节点数设计经验公式[9]:
(1)
式中,n为输入层神经元数目;m为输出层神经数目;d为 1~10 之间的整数。
5)最佳隐藏层单元数可参照以下公式[10]:
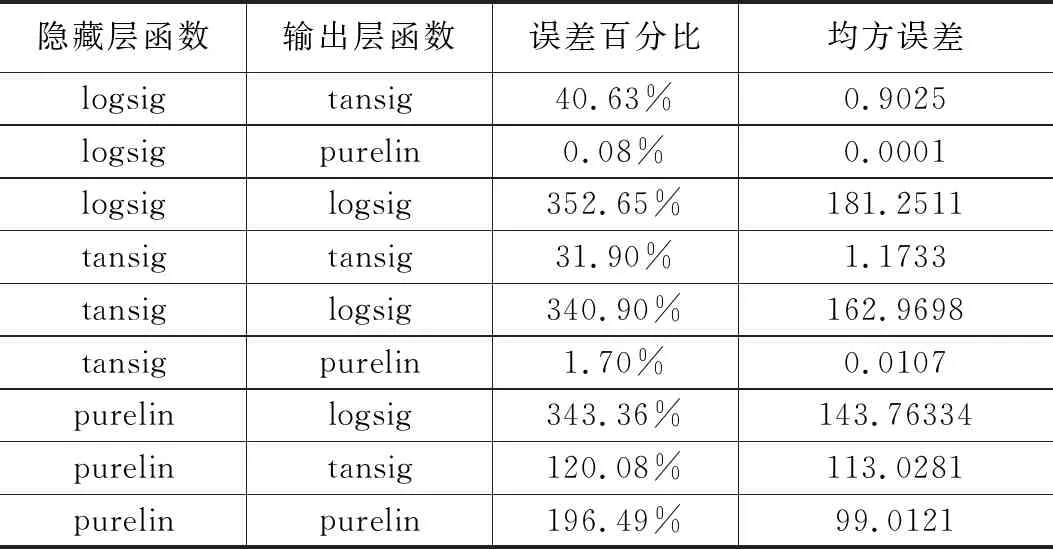
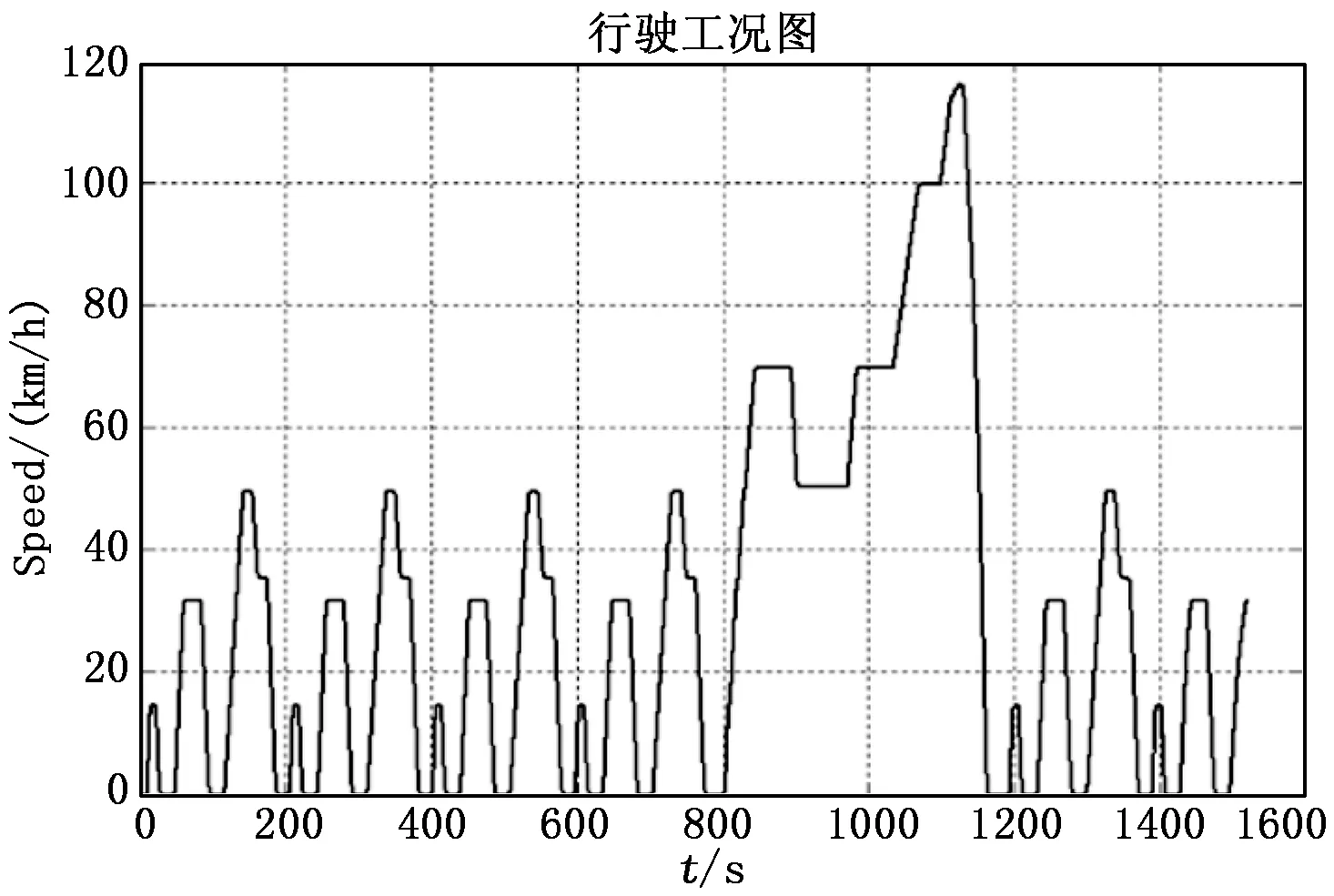
l (2) l=log2n (3) 式中,n为输入层单元数。 根据实验数据,采用数学规划的思想对神经网络构架进行选择。取模型训练至预测时间称为运算时间Ct,及每个预测点的平均绝对误差Ess为性能指标。Ess计算公式如式(4)。Ct与CUP性能、模型结构及算法等有关,运算时间Ct和平均绝对误差Ess作为设计模型的重要参考。 (4) 可以建立多目标线性规划模型来选择最优模型。其数学模型如下: minCt (5) minEss (6) s.t. 0≤Ct≤max(Cti) 0≤Ess≤max(Essi) 式中,i是按模型隐含层数划分的模型序号(i=1,…,5)。 Hornik, Cybenko等[11-13]表明,一个前馈神经网络如果具有线性输出层和至少一层具有任何一种“挤压”性质的激活函数的隐藏层,只要给予网络足够数量的隐藏单元,它可以以任意精度来近似任何一个有限维空间到另一个有限维空间的Borel函数。 在网络结构和阈值相同的情况下,BP神经网络预测误差和均方误差、输出单元激活函数的关系如表1[14]所示。隐含层和输出层激活函数的选择对BP神经网络预测精度有较大的影响。 在权衡收敛速度和预测误差后,用tan sig函数为隐藏层激活函数,purelin函数为输出层激活函数,它们的表达式为: (7) purelin(x)=x (8) tan sig和purelin函数图形如图1。tansig函数具有“挤压性质”。 图1 激活函数图形 tansig函数导数为: (9) 式中,a为常数,tansig函数导数的这个性质将导数运算转换为乘法运算可以节省大量的计算时间,同时也提高了运算精度。 虽然随机梯度下降(SGD)在一般的机器学习中是应用最多的优化算法,特别是在深度学习中,但其学习过程有时会很慢。动量方法可以加速学习,特别是处理高曲率、小但一致的梯度,或者是带有噪声的梯度。随机梯度下降和动量方法的结合,有利于神经网络性能的提升。Nesterov动量算法[15],是带动量的随机梯度下降算法,在凸批量梯度的情况下,Nesterov动量将额外误差收敛率从O(1/k)(k步后)改进到O(1/k2),有效减少了神经网络陷入局部最小值的风险。使用粒子群算法对权值和阈值优化,有效的提高了模型的泛化性能。 神经网络的学习率的取值在[0,1]之间,学习率越大,对阈值的修改就越大,网络学习速度越快。但是过大的学习率将使阈值学习过程产生震荡,过小的学习率使网络收敛慢,阈值难以稳定。变学习率在BP神经网络进化初期较大,网络收敛迅速,随着学习过程的进行,学习率不断减小,网络趋于稳定。变学习率计算公式为: (10) 基于上述深度神经网络模型的学习优化算法Nesterov动量算法和参数初始化算法RMSProp算法[16],两者相结合,在此基础增加了变学习率算法得到模型训练算法如下所示,式中用符号©表示Hadamard乘积。 基于Nesterov动量的RMSProp变学习率算法: Resquire:全局衰减率ρ,动量参数α Resquire:初始参数θ、学习率、速度v,初始累计变量γ=0 while 没有到达停止准则 do 从训练集中采含m个样本{x1,x2,…,xm}的小批量,对应目标为yi。 累计平方梯度:γ←ργ+(1-ρ)g©g 权值/阈值更新:θ←θ+v end 粒子群优化[17](Particle Swarm Optimization,PSO)算法是由Kennedy 和 Eberhart在1995年在受到鸟类觅食现象启发,提出的一种全局智能随机优化算法。PSO算法,每只鸟”被看作一个“粒子”。在R维解空间中第i个粒子的位置可表示为pi=(pi1,pi2,…,piR);第i个粒子的速度表示为vi=(vi1,vi2, …,viR)。第i个粒子在空间飞行路线中的最好点表示为ti= (ti1,ti2,…,tiR);粒子群内部所有粒子飞行过的最好的点表示为tg=(tb1,tb2,…,tbF),粒子群的每个粒子的速度和位置更新迭代公式为: (11) (12) 式中,wi为惯性权重,r1和r2为0到1的随机数,c1为局部学习因子、c2为全局学习因子。 对模型参数使用粒子群算法优化,避免了目标函数陷入局部最小值的风险,同时也提高了模型的训练速度和泛化性能。 过拟合(overfitting)是神经网络模型不可避免的,目前有两种常用于缓解神经网络过拟合的方法,第一种策略是“早停”(early stopping):将数据分成训练集和测试集,训练集用来计算梯度、更新权值和阈值,验证集用来估计误差,若训练集误差低但测试集误差升高,则停止训练,同时返回具有最小验证集误差权值和阈值。第二种策略是”正则化”(regularization)[10],其基本思想是在误差目标函数中增加一个用于描述网络复杂度的部分。 总优化算法流程如图2所示。 图2 模型算法流程 给定训练集D={(x1,y1),(x2,y2),…,(xm,ym)}xi∈Rs×m,yi∈Rn×m,即输入示例有s个特征属性描述,输出n×m实值矩阵。基于Nesterov动量的RMSProp变学习率算法参数迭代更新公式推导如下,符号说明如表2。 表2 符号说明 对训练集(xk,yk)假定网络输出为: (11) 网络在训练集(xk,yk)的均方误差为: (12) 参数更新估计式为: Δθ=θ+v (13) 以隐藏层到输出层的连接权值whj例来推导。给初始学习率,有: Δwhj=- (14) 临时更新: (15) (16) 根据uj的定义,显然有: (17) 输出层使用purelin函数,由式(11)和(12)有: (13) 累计梯度: rhj=ρrhj+(1-ρ)gj·gj (14) 速度更新: (15) 得连接权值whj更新公式: (16) 类似可以得到其阈值的更新公式: (17) 模型的输入为负载功率P、电流I、温度T及随机干扰信号D,输出为SOC预测值。训练数据采用温度为20℃下,纯电动车整车在CYC_NEDC(新欧洲行驶循环)工况下的8次循环中电池包的电流、负载功率、温度的0.1 s采样值,使用经预处理的15 381个高质量数据样本对模型进行训练和预测。整车参数如表3。8次新欧洲行驶工况曲线如图3,其对应的电池组参数变化曲线如图4,可看出SOC变化是高度非线性,并且受到老化、温度等多因素影响。使用如图5所示的干扰信号模拟随机因素对SOC估计的干扰。 表3 整车技术参数 运算时间在Intel(R)Core(TM)i7-4510U CUP@2GHz处理器,Matlab平台上对对电池包实验数据进行训练和预测所计算得到,因为不同的芯片运算性能不同,SOC预测时间也不同,但是模型的优化效果具有相同的趋势,这里对模型运算时间进行定性分析。 图3 8次CYC_NEDC循环工况曲线图 图4 电池组参数变化曲线 图5 随机干扰信号 参考神经网络模型设计经验并根据实验数据,利用多目标数学规划选择出不同深度的神经网络最优构架。由于神经网络训练和预测存在不稳定性,即每次训练和预测的结果存在细微差别,故每个构架进行多次训练和预测,对运算时间和平均绝对误差取平均值。采用传统Levenberg_Marquardt的BP训练算法作对比,其优化效果如表4所示,经过粒子群算法和基于Nesterov动量的RMSProp变学习率训练算法优化后,在保证SOC平均绝对误差满足工程要求的前提下,有效减少了运算时间,特别是单元数多的构架,这证明这套模型优化方法能快速找到最优的模型参数,减少迭代次数,从而减少运算时间,并且设计出的最优构架结构简单、SOC预测精度高,具有一定的参考价值。 表4 不同模型架构的优化效果 由不同构架的神经网络对电池SOC估计的结果分析,同一深度前馈神经网络SOC预测精度随着单元数的增多而减少,但是运算时间也增加。预测精度随着网络深度的增加而减少,运算时间增加。因此,在相同输入输出数据集条件下,神经网络运算时间与模型训练算法、模型构架和芯片性能有关。 根据行业标准,考虑到SOC估算时间及其平均绝对误差,还有模型结构复杂度和可靠性。选择优化后的双隐层,构架为[4 2 3 1]的神经网络模型作为锂电池SOC的估算模型,运算时间为0.460 7秒,SOC预测平均绝对误差为0.129 0,拟合曲线如图6所示,R值在每次运算时都能达到0.9,接近1,可见该模型稳定性高,预测精度可靠。并且期迭代77次左右时,残差已经收敛,达到期望误差。如果搭载神经网络专用芯片或性能更高的芯片,运算时间会进一步减少,实时预测成为可能。 图6 双隐层最优构架回归曲线图 分别使用同样的数据集,对径向基函数神经网络(RBF)、广义回归神经网络(GRNN)和Elman神经网络进行训练和预测,结果如图7所示。由图可以看出由于BP神经网络结构简单,结合上述优化算法,使其在动力电池状态估计上比其他常见的神经网络模型具有更少的运算时间和较好的预测精度。证明经过优化后的双隐层BP神经网络具有更好的工程实用性。 图7 常见神经网络模型SOC估计对比图 由整车实验数据,参考BP神经网络设计经验,研究更深的神经网络模型构架设计,对不同构架的神经网络进行了性能分析。针对这类模型SOC估计运算时间长、构架设计困难、对芯片性能要求高、无法实时预测等困难,使用能有效减少模型运算时间的粒子群优化算法和基于Nesterov动量的RMSProp变学习率训练算法,对模型进行了优化。SOC估计误差范围的条件下,运用数学规划方法选择一个平均绝对误差小且训练时间短、稳定性高并具有实用性的双隐层神经网络模型用于SOC估计。由于神经网络训练样本数没有理论指导,套模型优化方法与模型设计方法没有在训练样本数上进行研究,但为神经网络模型在电池其他状态估算上提供有价值的参考。随着神经网络专用芯片不断投入市场,神经网络模型电池状态估计有较大的应用前景。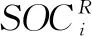

2 模型优化算法
2.1 模型训练算法

2.2 模型参数优化算法
2.3 过拟合优化措施
3 模型优化算法数学证明




4 前馈神经网络SOC估计结果与分析






5 结论
