简支转连续桥梁温度效应通用计算方法研究

盛可鉴，王景波

(黑龙江工程学院 土木与建筑工程学院，黑龙江 哈尔滨 150050)

温度场是指混凝土结构中在某一时刻各个位置的温度状态。桥梁受温度场的影响，主要有整体温度影响和局部温差影响两种方式。前者是指季节温差变化，也就是缓慢变化的常年环境温度。此时，应假定温度沿截面高度均匀变化。桥梁结构将沿着纵向移动，该移动可反应在伸缩缝、支座位移或柔性桥墩等水平变位方面，对结构的力学影响较小。而局部温差通常由于日照、强降温等引起截面内部不同位置处的温度发生非线性变化，在这种温度模式下，结构将产生温度次内力和温度次应力，很容易导致结构开裂，无论静定还是超静定结构均会发生此类问题。

我国的简支转连续梁桥多采用通用设计方法，也就是小箱梁及T梁结构的标准设计。《中国公路桥涵设计通用规范》(JTG D60-2015)中明确规定了我国公路桥梁设计时的温度模式，可按照面积等效及形心等效原则，将箱梁转化为等效T梁的计算模型[1]，如图1、图2所示。

温度应力一部分来自结构内部的自平衡温度应力，另外一部分来自外部的约束温度应力。由于混凝土内部的各层纤维间变形不一致而相互约束，所以会产生内部自平衡温度应力，此时，结构受力状态与结构所处的力学体系、边界条件等均无关系，无论静定结构还是超静定结构，只要处于结构内部的非线形温度场，都会产生内部自平衡温度应力。此外，当结构温度变形受到边界条件约束时，也会产生外部约束温度应力，这种约束应力只会在超静定结构中发生。结构温度应力理论上应该等于上述两种温度应力的和[2]。

图1 箱梁截面温度计算图式(单位：cm)

图2 T梁截面温度计算图式(单位：cm)

1 温度自应力计算

由于简支转连续结构的一般顶板厚度h1大于100 mm，所以局部温度梯度通常表示为

(1)

式中符号含义如图1、图2所示。

由温度梯度作用引起截面应变的曲率ψ、沿梁高y=0处ε0发生变形，计算式分别为

0.66b1]t2}-ycψ.

(2)

式中:A为截面的面积，α为材料的线性膨胀系数，I为截面的抗弯惯性矩。

温度梯度t(y)产生的温度自应力σs(y)为

σs(y) =E[α·t(y)-(ε0+ψ·y)].

(3)

式中:E为混凝土的弹性模量。

截面温度自应力为

σs(y=h) =E[α·t2-(ε0+ψ·h)];

(4)

σs(y= 0) =-E·ε0.

(5)

2 温度次应力计算

在温度场作用下，简支转连续梁桥结构会产生纵向长度变化，及竖向、横向的挠曲变形，支座将释放纵向伸缩变形，因此对主梁的影响较小。但竖向和横向的挠曲变形将会在支座处产生多余约束，同时会在结构中产生附加内力(温度次内力)。如图3所示，温度次内力可通过结构力学分析得出。

例如，一个n跨结构，中间墩支点的主梁负弯矩为未知力，此时，有n-1个未知力，对应的力法方程为

[δ]{x}+{Δt}=0.

(6)

式中:[δ]为结构柔度系数矩阵， {x}为结构赘余力矩阵，{Δt}为结构载变位矩阵。

{Δt} =-{ψL，ψL，ψL，…，ψL，ψL，ψL}.

(7)

图3 计算图式

该力法方程通过计算可得出温度次内力。

边墩墩顶位置的温度次内力和中间墩墩顶位置温度次内力为

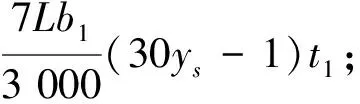
(8)

(9)

边跨：温度次内力效应计算式为

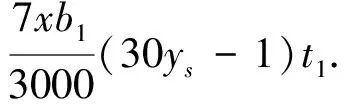
(10)

次边跨：温度次内力效应计算式为

(11)

中间各跨：两侧墩顶温度次内力效应相同，温度次内力效应计算式为

(12)

综上所述，得出简支转连续梁桥边跨、次边跨及各中间跨的温度次内力效应计算式，并将由此求得的温度次应力与温度自应力相加，得到温度总应力。

3 结 语

本文基于经典结构力学理论，通过对我国桥梁设计规范温度场作用下结构变形规律的分析，推导得出力法方程，由此得出混凝土温度内力效应力学通用计算公式，为简支转连续梁桥的设计及施工提供技术支持。