时延QoS约束下的混合业务带宽估计

孙洪亮 沈伟达 郭艳年

摘要：本文研究时延QoS（Quality of Service）约束下，通信网络中混合业务的带宽估计问题。系统模型中，采用多流输入的排队系统去抽象混合业务到达的网络，用中断泊松过程（Interrupted Poisson Process，IPP）描述标签流，用泊松（Poisson）过程描述背景流。利用排队论及有效带宽理论，估计了IPP+Poisson混合业务的带宽需求。仿真验证了带宽估计结果可以满足时延QoS要求。

关键词：带宽估计;QoS;混合业务;排队论;有效带宽

中图分类号：TN929.5 文献标识码：A 文章编号：1007-9416（2020）03-0018-02

0 引言

近年来，随着用户对移动互联网和多媒体业务需求的快速增长，网络业务种类也在不断增加。业务的多样化，给网络带宽资源分配带来了更大的挑战。准确的带宽估计，是带宽资源高效分配的前提，因此，研究多业务到达下的带宽估计问题，意义重大。通信网络中业务流量的到达具有随机性，同时对服务质量（Quality of Service，QoS）有着一定的要求，因此增大了带宽估计难度。一些学者针对带宽估计问题展开了研究[1-3]。而目前研究主要针对单一业务到达的系统，对于混合业务到达的系统，研究还并不多。本文用中断泊松过程（Interrupted Poisson Process，IPP）抽象标签流，用泊松（Poisson）过程抽象背景流，建立了混合业务到达的排队系统，借助有效带宽理论，估计了时延QoS约束下的带宽需求。研究目的在于为通信网络的带宽资源分配提供一定的指导，进而提高资源利用率。

1 系统模型

本文建模分析了混合业务到达（IPP+Poisson）、单一服务的队列系统。为研究业务所需带宽，将服务过程建模为常速率服务，用以表征带宽。假设系统以先到先服务的方式服务，系统排队模型图如图1所示。

下面来分别介绍两个到达业务流。第一个业务流是IPP流，描述IPP到达过程的马尔可夫链如图2所示。其中，表示保持在1态的概率，表示保持在2态的概率。当IPP到达过程转移到2态时，到达服从参数为的Poisson分布。

第二个业务流是Poisson流，Poisson到达过程的描述如式（1）所示。其中表示Poisson到达的强度，xn表示在第n个时隙到达数据包的数量。P（xn=k）表示在第n个时隙内有k个数据包到达的概率。

（1）

IPP流和Poisson流叠加后符合马尔可夫调制的泊松过程（Markov-modulated Poisson Process，MMPP）[4]。在IPP流和Poisson流的混合流分析中，可以将之等效为MMPP流，这样可以将一个复杂的混合流分析转化为单一到达流分析。在MMPP流中，我们令A（n）表示从初始的时刻到时隙n时数据包的累计到达数量。

我们用S（n）表示前n个时隙累计服务的数据包数量。令L（n）表示在时隙n时的系统队长，队长的演化趋势可以表示如下：

（2）

其中w +=max{0，w}。

2 业务带宽估计

本文所估计的带宽主要依赖于有效带宽理论。有效带宽指的是在给定QoS要求前提下，到达流量所需的最小带宽。在MMPP源的有效带宽EB基础上，我们进一步考虑了系统的带宽利用率，给出MMPP源的带宽需求ERB如下所示：

（3）

其中，u（F） 表示矩阵F 的最大特征值。Q为Markov转移矩阵，为速率对角矩阵，θ为QoS指数。和Q 的计算方法[5]如下：

（4）

（5）

其中，和分别是泊松到达的速率和指数分布逗留时间的平均值，i =1，2，表示MMPP到达过程的马尔可夫链所处状态。

为了保证统计时延QoS要求，带宽需要保证下面不等式成立：

（6）

其中，d（n） 表示时延，D表示目标时延，表示时延违反概率阈值。QoS参数可根据式（6）确定。根据李特尔公式，时延d（n） 可以表示为下式：

（7）

其中，表示MMPP的平均到达速率。

通过以上分析，我们知道，通过系统业务到达参数、QoS指数及带宽利用率，即可求出业务源的带宽需求ERB。

3 仿真分析

混合流为IPP流和Poisson流的聚合，服务采用常速率服务。仿真工具采用Matlab，仿真中将时延违反概率阈值设置为=10-3，到达参数设置为λ0=2 packets/slot，λ1=1 packets/slot，=0.5、=0.6。

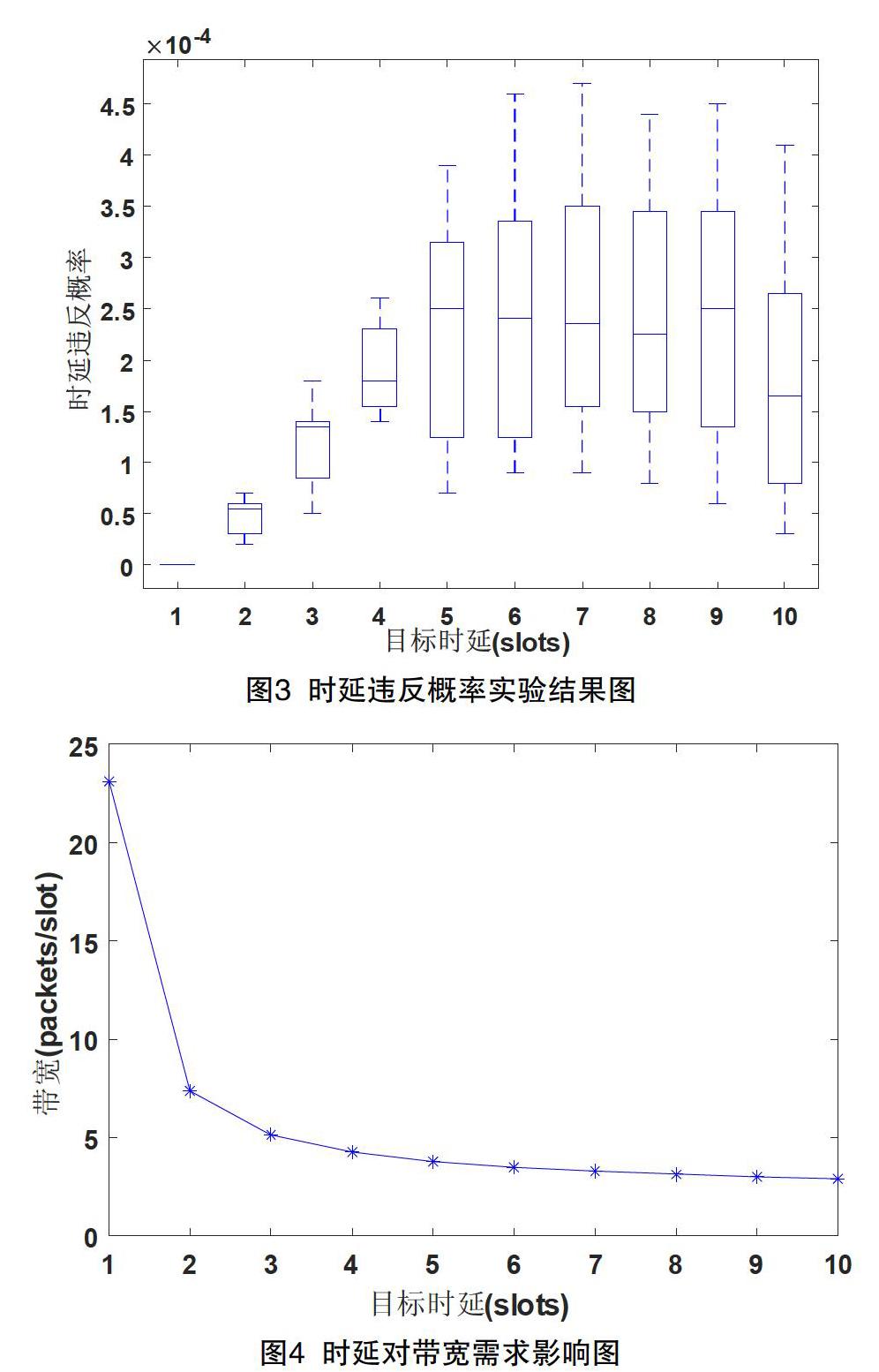
为了验证模型估计的带宽可以满足业务时延QoS要求，我们模拟了一个队列系统的到达过程和服务过程，生成了两种类型的流量，对时延违反概率进行了计算。实验结果如图3所示。从仿真结果可以看出，时延违反概率始终要小于预先设定的时延违反概率阈值10-3。说明本文模型计算的带宽结果，可以满足业务的时延QoS要求。

随后，讨论了时延QoS参数D 对带宽需求的影响，仿真结果如图4所示。结果表明，随着目标时延D 的增加，业务的带宽需求不断降低，而且降低的幅度逐漸趋于平缓。因为当目标时延逐渐增大时，系统的时延要求越来越宽松，所需带宽越来越少。随着时延QoS变得越来越宽松，带宽需求将逐渐趋向于流量的平均到达率。

4 结语

本文研究了时延约束下混合业务带宽估计问题，建立了IPP+Poisson到达的网络队列系统。研究中将IPP和Poisson等效为MMPP业务流进行分析，借助有效带宽理论推导了满足时延QoS要求下混合业务的带宽需求。仿真分析给出了时延QoS参数对带宽的影响，该研究可以指导网络资源的带宽管理和带宽分配。

參考文献

[1] 张志飞，王黎伟，裘正定.时延约束下的等效带宽估计[J].通信学报，2000（12）：73-77.

[2] ANJUM B，PERROS H.Bandwidth estimation for video streaming under percentile delay，jitter，and packet loss rate constraints using traces[J].Computer Communications，2015，57：73-84.

[3] Ricardo O S D，Sperotto A，et al.Towards Bandwidth Estimation Using Flow-Level Measurements[J].Lecture Notes in Computer Science，2017，7279：127-138.

[4] Geleji G，Perros H.Jitter analysis of an IPP tagged traffic stream in an {IPP，M}/M/1 queue[J].annals of telecommunications-annales des télécommunications，2014，69（5-6）：283-294.

[5] ANJUM B，PERROS H，MOUNTROUIDOU X，et al.Bandwidth allocation under end-to-end percentile delay bounds[J].International Journal of Network Management，2011，21（6）：536-547.

Abstract：This paper investigates the bandwidth estimation for mixed traffic in the communication networks under delay QoS （Quality of Service） constraints. In the system model， the queuing system with multiple stream input is used to abstract the networks with mixed traffic. The interrupt Poisson process （IPP） is used to describe the tagged traffic， and the Poisson process is used to describe the background traffic. Based on the queuing theory and effective bandwidth theory， the bandwidth requirements for IPP+Poisson services is estimated. Simulation results show that the bandwidth estimation results could meet the delay QoS requirements.

Key words：bandwidth estimation;QoS;mixed traffic;queuing theory;effective bandwidth