含多端柔性多状态开关的主动配电网动态潮流
2020-06-04曾永浩叶家雄潘志图李明琪何奉禄张诗建
曾永浩,叶家雄,潘志图,李明琪,何奉禄,张诗建
(1.广东电网有限责任公司佛山供电局,广东 佛山528500;2.广州市奔流电力科技有限公司,广东 广州 510635)
伴随大量分布式电源(distributed generation,DG)等灵活性资源的接入,配电网逐渐由无源被动向有源主动转变,结构与运行特性亦发生巨大变化[1-4];同时,DG出力也增加了配电网潮流的多向性和复杂性。在此背景下,依赖传统“硬”开关的运行调节方式无法满足配电网主动、快速、灵活调度与控制的需求。柔性多状态开关(flexible distribution switch,FDS)作为一种可灵活控制潮流的电力电子设备,为供电方式优化提供了新的思路[5-6]。与传统开关设备相比,FDS兼具开环和闭环运行的优势,且可保障迅速响应、灵敏动作、灵活切换的工作特性。
针对FDS及其优化运行,国内外学者和机构已开展相关研究。2009年,英国帝国理工学院首次提出软常开开关(soft normally open points,SNOP)的概念;2015年,帝国理工学院和卡迪夫大学进一步提出了智能软开关(soft open point,SOP)的概念及典型拓扑,并在英格兰南部建设了33 kV、20 MVA的两端柔性开关示范工程。国内学者和机构也进行了柔性开关的相关研究,并对其发展概况进行综述[7-11]。2015年,天津大学提出了智能配电FDS的概念,它是SOP在功能上的拓展和应用场景上的延伸;同时针对含FDS的配电网优化运行问题,从静态和动态潮流优化等方面开展了研究[12-13],提出或研究含FDS配电网无功电压优化运行模型与方法[14-15]、FDS优化配置问题[16]、传统联络开关和软开关并存的优化方法[17]、计及FDS智能配电网调控技术[18-20]。武汉大学将潮流介数的概念应用于SNOP的配置分析及优化[21]。上述研究中,对配电网可调因素的考虑还不够充分,未能实现FDS和其他配电网调节组件的协调配合,而且针对含多端FDS配电网的实际工程与应用的仿真验证亦未能有效开展。
针对以上问题,本文将含FDS配电网的优化运行研究拓展到多调节因素联合优化的范畴,开展计及多端FDS的主动配电网动态潮流分析研究;针对配电网常规可调组件设定严格的约束条件,并定义负荷安全裕度、功率增量配比和潮流均衡度指数来描述潮流的转移分布特征。在此基础上,依托南方某地区含FDS智能配电网示范工程展开仿真验证,为FDS在实际配电网中的推广应用提供参考。
1 FDS运行特性及数学模型
1.1 FDS运行特性
FDS可以通过电压源型变流器实现,图1为FDS与交流配电网相连时的系统结构图。
由图1可知:不同的上级电源下送有功功率P和无功功率Q,通过FDS实现均衡分配;因为馈线存在阻抗R+jX,功率的多向流动亦造成损耗;FDS内部的直流母线通过稳压电平实现阀侧电压Udc的恒定。FDS中的变流器采用直接电流控制策略进行控制,该策略控制系统为双环控制结构,即功率外环和电流内环。为了保证运行安全,FDS需维持直流侧电容电压于其额定值附近;该运行约束即为FDS与两端交流系统之间的有功功率交换必须保持平衡,而与两端交流系统间的无功功率交换由于不需要直流侧电容的参与则相互独立;因此,从配电网潮流运行层面看,FDS对于交流配电网系统而言,具有以下运行外特性:在维持直流侧电压稳定的前提下,可协调各个端口的有功功率使其满足有功平衡,亦可独立调节每个端口的无功功率。
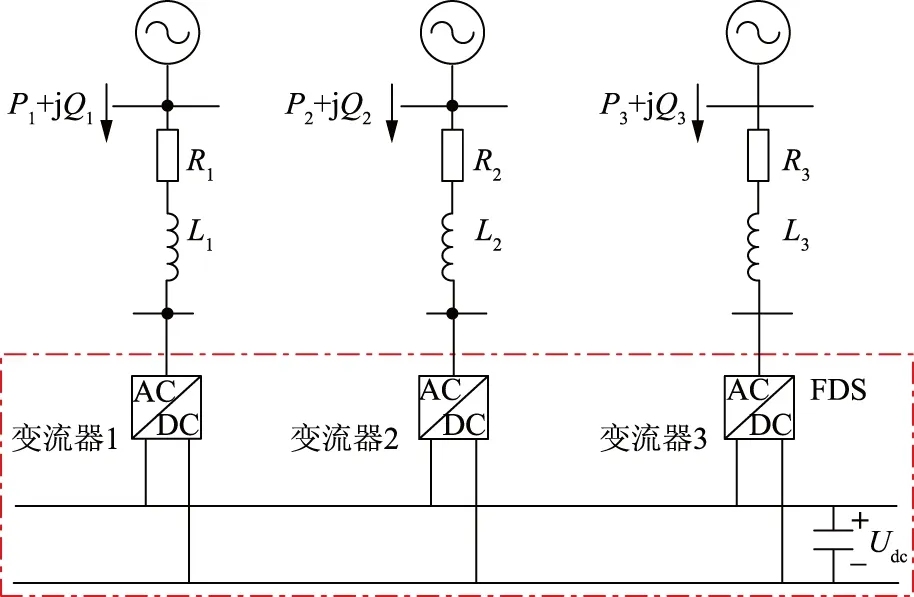
图1 含FDS的主动配电网
1.2 FDS数学模型
依据FDS的实际工作方式,所有端口的有功功率和有功损耗之和为0,同时每个端口具备无功功率独立调控的功能[22];因此将端口的功率关系描述为
(1)
式中:Pi,t,fds、Qi,t,fds、Li,t,fds分别为t时刻与节点i所连端口的输出有功功率、无功功率和有功损耗;Qi,max,fds和Qi,min,fds分别为t时刻与节点i所连端口的无功功率上下限。
FDS本身具有无功功率独立调节的作用,因此不考虑无功损耗。FDS的有功损耗主要来源于不同子模块,包括整流侧变流器、逆变侧变流器等子模块的损耗。从FDS的电气建模角度出发,将上述有功损耗归类为3部分[23]:①空载损耗,与维持设备正常运行有关;②恒电压损耗,与FDS各端口的电流成正比;③恒阻抗损耗,表示为FDS各个端口的电流的二次函数。有功损耗描述为
(2)
式中:Ii,t,fds为t时刻连接在节点i的FDS端口电流;ai,fds、bi,fds和ci,fds分别为FDS的端口损耗系数。
在含FDS的配电网中,FDS端口的电压通常运行在标准电压附近,则端口的电流大小由该端口的视在功率Si,t,fds决定,当端口电压取标幺值(约为1)时,描述为
(3)
对FDS的端口有功损耗约束作线性近似处理,则式(2)可表示为
Li,t,fds=αi,fdsSi,t,fds+βi,fds.
(4)
式中αi,fds和βi,fds为对FDS的端口有功损耗作线性近似处理后的系数。
2 含FDS的主动配电网动态潮流模型和指标
2.1 潮流模型和运行约束
在所述模型中,约束条件包括配电网潮流方程约束、节点电压和线路电流约束、电容器和静止无功补偿装置运行约束,以及FDS运行约束,具体如下。
a)配电网潮流方程:
(5)
(6)
式中:Pi,t,G、Qi,t,G、Pi,t,DG、Qi,t,DG、Pi,t,d、Qi,t,d分别为在t时刻连接在节点i的发电机、DG和负荷的有功功率和无功功率;Qi,t,CB为连接在节点i的电容器的无功功率;Pij,t和Qij,t表示节点i流向节点j的有功功率和无功功率;Pji,t和Qji,t为节点j流向节点i的有功功率和无功功率;rij和xij分别为线路ij的电阻和电抗;Iij为线路ij的电流;Ui,t和Uj,t分别为节点i和j的电压幅值。
b)节点电压约束:
(7)
式中:Ui,min和Ui,max分别为节点i的电压上下限;N为节点数;T为系统运行周期。
c)线路电流约束:
(8)
式中:Iij,max为线路ij的电流幅值的上限;E为线路集合。
d)电容器运行约束:
Qi,t,CB=ki,tΔQi,∀t∈T,ki,t=0,…,Ki.
(9)
式中:ki,t为在t时刻连接于节点i的电容器的投切组数;Ki和ΔQi分别为连接节点i的电容器最大投运组数和单组容量。
e)变压器运行约束:
(10)
式中:κij,t为t时刻变压器的变比;κij,min为变压器的分接头位于最小档位时的变比;mij,t为变压器分接头档位;Δκij为变压器变比的调压步长;Kij为变压器分接头档位数。
f)分布式电源运行约束:通过功率因数实现DG有功、无功出力耦合,进而简化约束的形式;约束表征DG外部出力特性,实现功率注入的配电网调节作用。
(11)
式中:Pi,t,DGpre为DG有功功率最大跟踪值;fi,lead和fi,lag为DG的超前和滞后功率因数。
g)FDS运行约束:在运行过程中,FDS端口视在功率不能超出其上限,运行约束须考虑
(12)
式中Si,max,fds为与节点i所连端口的视在功率上限。
2.2 目标函数
在本文模型中,可根据配电网的实际运行需求,选择供电损耗与电压偏移之和最小为目标函数,均取标幺值形式,如下:
(13)
2.3 潮流指标
除了常规的电压和网损指标外,本文同时引入对潮流转移均衡度的定量描述,以分析FDS作用下系统内的潮流转移分布特征,并建立适应的指标来描述该特征。分别定义出负荷安全裕度、功率增量配比和潮流均衡度指数,具体如下。
系统负荷在当前运行方式下从基准点开始负荷逐渐增长,直到约束越限,定义此时系统总负荷对基准总负荷的相对变化率为该运行方式下的负荷安全裕度,表达式描述为
Lc=(Lex-Lbase)/Lbase.
(14)
式中:Lc为负荷安全裕度;Lex为越限时系统总负荷;Lbase为系统基准总负荷。
将线路中单位负荷变化量下的功率增量与其功率裕度的比值称为功率增量配比。通常,功率增量越大,或功率裕度越小,线路越容易越限,不利于系统安全运行,而此时的功率增量配比就会越大;因此,该指标能够在一定程度上反映负荷变化时系统各线路的安全程度,表达式如下:
(15)
式中:Pij,t,mrg为线路ij的功率裕度;Pij,max为线路ij的有功上限;ΔPij,t为t时刻线路ij的功率增量;prij,t为线路ij的功率增量配比。
基于实数信息熵[24]理论,定义潮流均衡度指数
(16)
式中:μ(ij)为线路ij的功率增量配比与所有支路功率增量配比之和的比值;R为潮流均衡度指数;C为常数,用以调整熵值范围。
3 模型优化
从数学优化角度来看,本文所述含FDS的主动配电网潮流模型属于一个混合整数非线性规划模型[25],其求解效率较低,且往往难以获取全局最优解。根据前文约束形式,可将非凸约束通过二阶锥变换转化成凸约束,并通过降阶将高次约束线性化,将整数变量转化成实数变量,提升模型求解效率。
3.1 二阶锥松弛
根据该模型的数学形式,可通过凸转化方式,将其转化为二阶锥规划模型。本文通过支路潮流构建方法描述了配电网功率平衡关系,式(6)属于非凸源,将其转化为标准二阶锥形式,如下:
(17)
针对FDS端口视在功率限制的非线性约束式转化为旋转二阶锥形式,如下:
(18)
FDS端口有功损耗式(4)属于非线性约束,对其作松弛处理,表示成标准二阶锥形式,即
(19)
3.2 降阶线性化
(20)
式中hm为引入的连续变量。为保证变压器分接头所接档位只有一个有效,引入二进制变量Bij,t,m,trans来描述变压器每个档位的有效性,且令变压器所有档位对应二进制变量之和为1。
3.3 整数变量转化
本文模型混合了整数变量,求解时的分支定界会占用额外计算资源,于是引入实数辅助变量Bi及相应约束对涉及的整数变量进行转化,如下:
(21)
式中Cmax和Cmin为整数变量z定义域的上下限;二进制变量Br限制2的r次幂项的有效性。
4 算例分析
4.1 算例简介
本文依据南方某地级市示范工程的实际配电网结构和运行数据,构建以FDS实现柔性互联的33节点测试系统,如图2所示。系统包含3条独立馈线,分别以节点1、12和23为主电源点;在节点19和22接入分布式光伏,设置其最大有功跟踪值作为其可调上限,且在0.95恒功率因数下运行;在节点8、20和24处连接相同的分组投切电容器,每组补偿容量25 kvar,共8组;在节点4、15和26处装设可调变压器,变比可调范围为4×2.5%;FDS端口分别接入节点11、13和29。
FDS是基于模块化多电平换流器(modular multilevel converter,MMC)结构,因此本算例将差异化端口的容量设置,以交叉多种运行场景下的潮流分析。场景设置见表1。
4.2 含FDS主动配电网动态潮流分析
为分析算例系统在各场景下的电压和网损情况,统计出各场景在不同端口容量设置(方式1为6 MVA/ 6 MVA/6 MVA,方式2为5 MVA/ 7 MVA/6 MVA)下测试得到的配电网损耗总能量、电压最大偏移值以及分布式光伏弃光率。其中,在区域配电网采用弃光率指标,旨在对比分析不同场景下光伏机组出力的差异性。具体指标结果见表2。
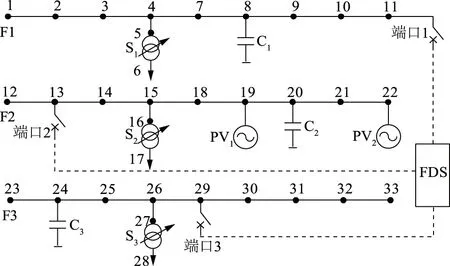
图2 三馈线互联测试系统
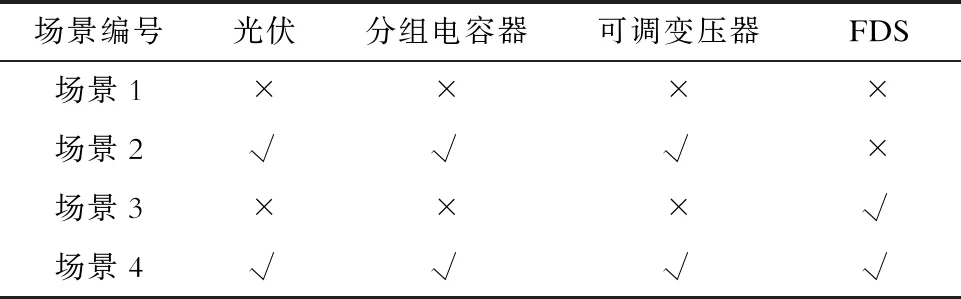
表1 算例系统的运行场景

表2 模型潮流指标
由表2可知:FDS装置调控(场景3)比常规组件调控(场景2)在降低配电网损耗、抑制电压方面和降低光伏弃光率方面效果更明显;若结合两者共同协作(场景4),则对以上配电网的优化效果得到进一步提升。其中,相同端口容量设置下,整体降损比例达30.6%,最大电压偏移降低83.3%,光伏弃光率降低9.2%;相比之下,当差异化设置端口容量时,降损比再提高19.7%,最大电压偏移值再降低5%,光伏弃光率再降低0.4%。可见,以FDS为媒介的负荷转供通道,优化配电网潮流基本参数,同时使DG的消纳场景更加丰富,提高其利用率。
为分析潮流的分布特征,对比各运行场景下的负荷安全裕度和潮流均衡度指数,结果见表3。
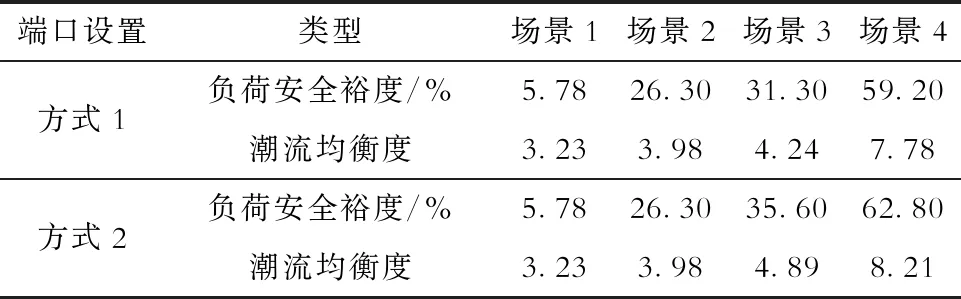
表3 负荷安全裕度和潮流均衡指数
由表3可以看出:常规调节组件和FDS的加入均能在一定程度上提高系统的负荷安全裕度,分别提升了20.52%(场景2)和25.52%(场景3);而场景4在2种调节手段的相互配合下,裕度提升效果最显著,提高了10倍左右。潮流均衡度指数反映系统各支路承担负荷功率变化的分配均衡度,由表3可知:场景4的潮流均衡度最高,代表负荷变化在系统各线路上的分配最均衡,说明此时系统能通过自身有效调节,合理分配潮流增量,均衡分摊负荷压力,提高系统供电的稳定性和可靠性;同样地,相比于相同端口容量设置,差异化的配置方法进一步优化了包含FDS参与调控下的配电网负荷安全裕度和潮流均衡度指数。
为进一步分析各线路功率增量配比与配电网运行工况的联系,绘制出场景1和场景4在测试周期内各线路的功率增量配比最小值分布情况,分别如图3和图4所示。
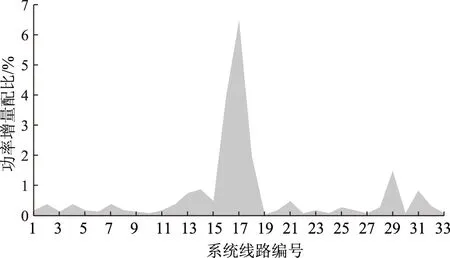
图3 场景1下功率增量配比分布
由图3可知:场景1下功率增量配比分布极不均衡,表现为少数支路的功率增量配比过高,即该部分支路呈现出应对负荷变化的安全程度降低,进而成为限制系统负荷安全裕度提升的关键因素;而场景4下功率增量分配更加均匀且幅值得到整体削减,局部峰值得到平抑,大幅提升系统的负荷安全裕度。对比不同的端口容量设置,可见差异化方案进一步削减了配比峰值,均衡功率增量配比的分布。
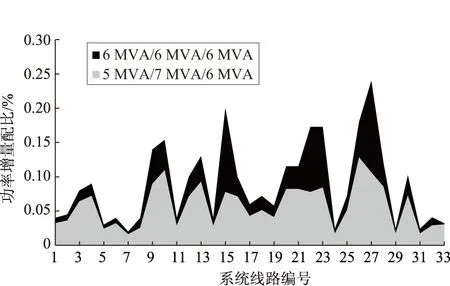
图4 场景4下功率增量配比分布
综上分析,在FDS参与潮流调控的场景中,通过差异化端口容量的设置,均能实现系统对负荷变化的安全承受能力的提升,以及潮流变化的均衡优化,使得通过柔性互联的馈线具备更高的运行安全性和供电可靠性。差异化方案的优化机理在于:负荷分布的差异致使馈线容量裕度的不同,而差异化的端口设置给予转供通道的合理布置和对接,进而充分地发挥了各馈线的转供能力。
4.3 算法效率
为探究本文二阶锥规划的可行性,并与其他模型求解方法(非线性规划调用SCIP)进行比较,列出各方法的计算参数,见表4。
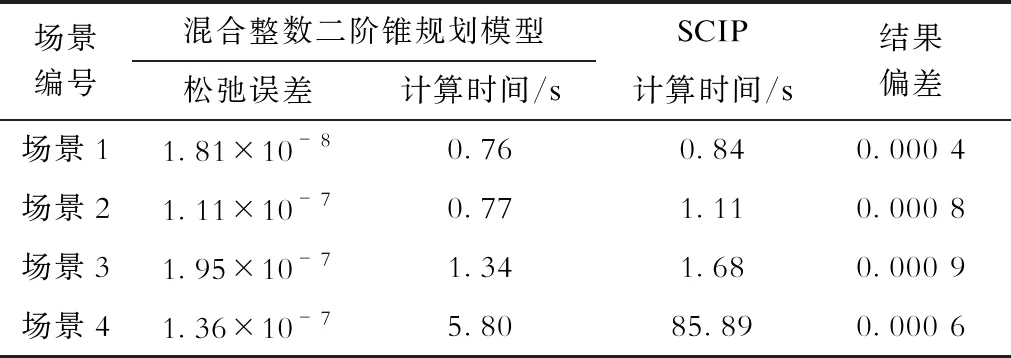
表4 规划方法的计算指标对比
由表4可知,相比于非线性规划应用,二阶锥规划的计算效率高,且当计算量越大时,松弛为二阶锥的方法使计算效率的提升越明显。2种方法的计算结果偏差均低于0.001,且松弛为二阶锥的最大误差数量级仅为10-7,满足本文优化求解的精度要求。
5 结论
本文在分析FDS结构特性和数学模型的基础上,建立含FDS主动配电网动态潮流模型,通过二阶锥松弛等方法优化模型规划,并依托实际示范工程,在三端FDS测试系统上对FDS与主动配电网的协调优化运行进行仿真实验,得到以下结论:
a)通过实际配电网模型的测试,FDS与主动配电网调节组件的协调配合可大幅降低系统损耗,减少系统电压偏移状况,并显著提升分布式电源利用率。
b)配电网借助FDS和常规调节组件的协同运行,可显著提升系统应对负荷变化的安全承受能力,并均衡各条支路的潮流分布;合理的差异化端口容量设置可高效利用各接入点的容量裕度,并进一步改善配电网的运行工况。
c)建立含FDS主动配电网的动态潮流模型,考虑常规调节组件的断面限制约束,通过二阶锥松弛、降阶线性化和整数变量转化,可大幅提升模型求解效率,保障寻优精度和稳定性。
