基于谐波分次检测与重复控制的配电网电能治理装置设计

黄彦璐, 林跃欢, 罗俊平, 姚知洋

(1.南方电网科学研究院有限责任公司，广东 广州 510663；2.中国南方电网有限责任公司，广东 广州 510623；3.广西电网有限责任公司电力科学研究院，广西 南宁 530015)

随着经济的发展，电能用量飞速增长，产生了各种电能质量问题，如用电负荷增加产生的无功功率不均衡、用电负荷分布不均产生的三相功率不均衡、非线性负荷产生的谐波电流污染等。在无功和不平衡补偿、谐波补偿等方面，国内外专家提出了静止无功补偿器、静止无功发生器、有源电力滤波器等先进的电力电子装置。目前的配电网电能治理装置通常具备上述多种功能，可应用于多种电能治理场合，具有较高的适应性和实用性[1-3]。

谐波电流检测与并网电流控制是配电网电能治理装置的关键技术之一。针对谐波电流检测，常用的方法有基于频域的检测方法和基于时域的检测方法[4]。基于多同步旋转坐标变换的谐波检测算法是一种常用的基于时域的检测方法，其可以有效检测基波及各次谐波对应的正、负序电流[5-6]。在三相四线应用场合，利用单相谐波检测方法可以检测零序电流中各次谐波的分量[7-8]；因此，基于多同步旋转坐标变换的谐波检测算法适用于全补偿模式和选择次谐波补偿模式，而后者在补偿电流超过装置的补偿能力时，可以选择其中的关键部分进行补偿，从而提高电能治理装置的灵活性[9-10]。

文献[5]提出一种基于多同步旋转坐标变换的指定次谐波电流控制策略，能够实现谐波选择次补偿功能；但该方法中各次谐波之间存在耦合情况，且由于谐波控制器设置于谐波检测结构内部，使得反馈回路带宽受限，降低了系统稳定性和响应速度。文献[10]提出一种谐波分次检测结合集中电流环的控制策略，使得谐波检测结构与电流控制器相互独立；但该方法未给出高效的谐波电流检测方式，且由于采用谐波幅值相位校准实现无静差跟踪，需要通过传递函数模型来计算各次谐波在指定频率范围内的增益和相移，对模型精确度的要求较高，故对于滤波器参数变化和电网阻抗、频率变化的适应性较差。文献[11-14]采用准比例谐振控制器对谐波电流指令进行控制，在不同次数的谐波补偿场合仅需要修改各次控制器的控制参数即可，灵活性较高；但该方法在多次谐波控制时计算量较大，且离散化准比例谐振控制器在高频段的频率适应性较差，需要额外的频率修正计算，在电网频率波动范围大时稳态误差也会相应增大。

本文提出一种基于谐波分次检测与重复控制算法的三相四线制配电网电能治理装置控制方案。其中谐波分次检测采用改进的多同步旋转坐标变换谐波检测法，其相比传统算法在滤波器同等响应速度下能够更精确地检测被测电流的基波有功、无功分量与谐波分量、不平衡分量，适用于常见的无功、谐波和不平衡补偿场合。重复控制算法能够对给定的补偿电流指令实现无静差跟踪，实现方法简单且占用计算资源少，其与比例积分(proportional integral,PI)控制器结合形成的复合控制器能够提高系统的动态响应，弥补重复控制器存在的一个周期延迟特性的不足。

1 基本拓扑与控制结构

本文采用的三相四线制配电网电能治理装置如图1所示。其中：主电路采用三电平拓扑，具有输出电压谐波含量低、器件电压应力小等优点；滤波器采用LCL滤波器，其中L1x(x取a、b、c)、L2x、Cfx分别为桥臂侧电感、网侧电感与滤波电容；Rcx为阻尼电阻，用于提高系统稳定性；Cdc1、Cdc2分别为正负半母线电容，电容中点引出与电网中线相连，构成分裂电容式三相四线结构;A、B、C为电网三相。

许多文献已给出三相四线制配电网电能治理装置的数学建模[15-19]。数学模型主要分为直流侧电容建模与LCL滤波器建模。针对直流侧电容模型，在三相四线制下通过控制桥臂电流的有功分量可以实现对直流母线电压的控制，通过控制桥臂电流的零序分量可以实现对母线中点电压偏差的控制。针对LCL滤波器模型，通过控制桥臂输出电压可以控制桥臂输出电流，进而控制并网电流。实际设计时通常采用较小的滤波电容以减少无功电流吞吐量，此时可近似认为并网电流与桥臂输出电流的基波分量相等；由此，可以得到三相四线制配电网电能治理装置控制结构如图2所示。其中vdc1、vdc2为直流正负半母线电压，ia、ib、ic为负载三相电流，i1a、i1b、i1c为桥臂输出三相电流，vsa、vsb、vsc为并网点三相电压，via、vib、vic为桥臂输出三相电压。

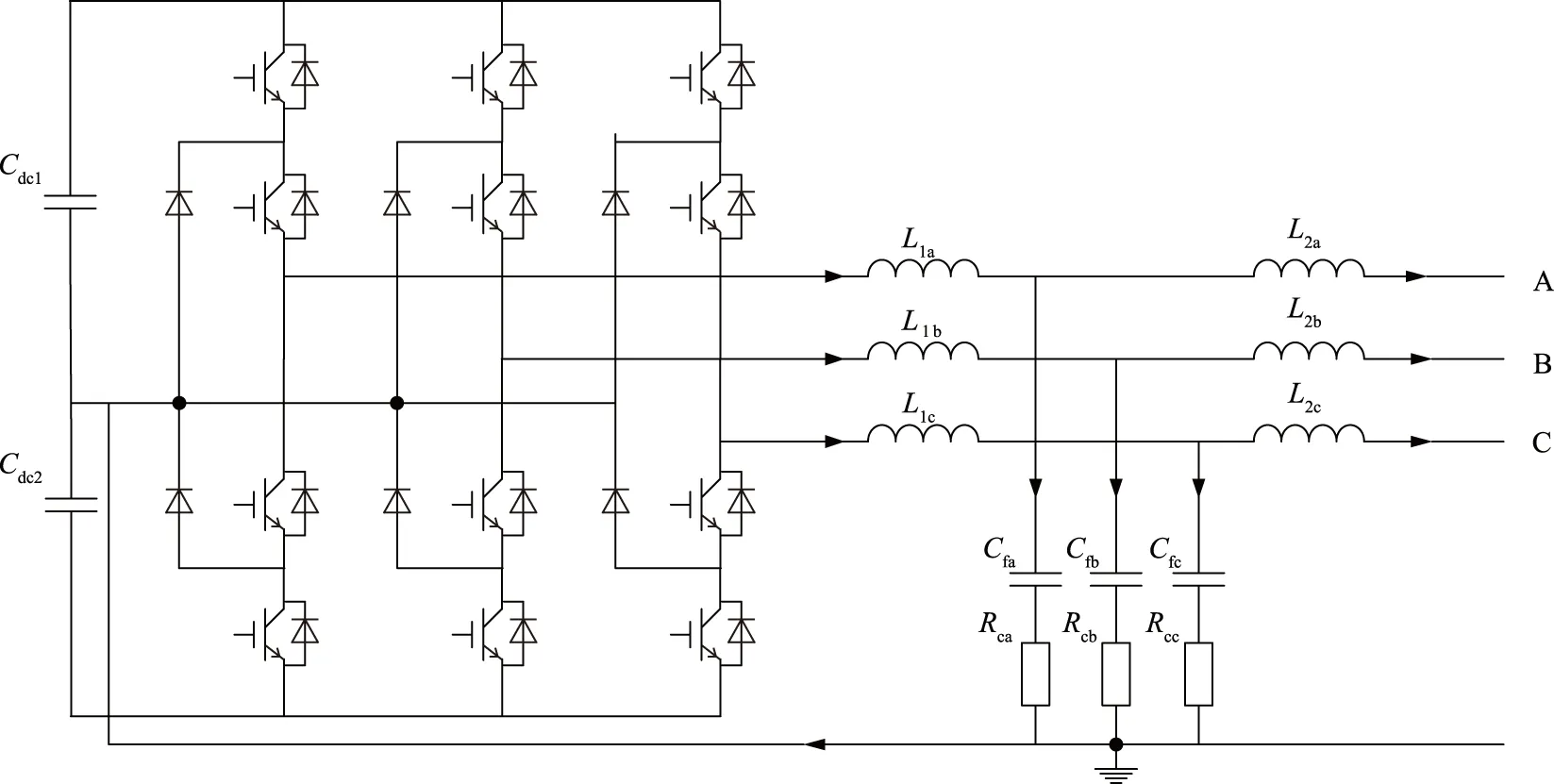
图1 三相四线配电网电能治理装置基本拓扑

2 谐波分次检测算法分析与设计

本文采用的谐波分次检测算法总体结构如图3所示。其中ia、ib、ic经过Clark变换后分为包含正负序信息的α、β分量和包含零序信息的γ分量iα、iβ、iγ。其中iα、iβ分量通过不同频率的Park变换得到各次谐波对应id、iq分量(idn、iqn,n=1,2,…)，不同次谐波的检测结果通过负反馈的方式实现检测结果之间的相互解耦；γ分量通过不同频率的单相旋转坐标变换得到各次谐波零序分量的信息，同样通过负反馈的方式实现检测结果解耦。

零序旋转坐标变换定义如下

(1)

(2)

式中：ωn为n次谐波角速度；t为时间。

针对正序负谐波检测结构，可以求得第n次谐波检测开环传递函数为

(3)

式中s为拉氏变量。

系统总体开环传递函数即为各个谐波检测环节开环传递函数之和，其形式为

(4)

由此可以求得第n次谐波检测的闭环传递函数为

(5)

对比如下形式的一阶低通滤波器

(6)

取τk=5 ms，n=1，k取-1、±5、±7、±11、±13，绘制基波正序分量检测传递函数Tf1(s)与传统1阶低通滤波器Gf1(s)的频率特性如图4所示。

由图4可知：基波正序分量检测环节包含对±5、±7、±11、±13次谐波的衰减，使得这些频率的谐波分量理论上不会出现在基波正序分量检测结果中；同时，在其他频率点处，谐波检测环节表现为带通滤波器特性，对远离中心频率的高次谐波具有较好的抑制效果。对比传统一阶低通滤波器的频率特性曲线可知，本文提出的谐波检测方案在同等滤波时间常数下的带宽与传统滤波器基本一致，故可以认为二者的响应速度近似相等。滤波时间常数的选取可以根据系统带宽的需要进行设计。

SPWM—正弦脉冲宽度调制，sinusoidal pulse width modulation的缩写。

图2 三相四线配电网电能治理装置控制结构

Fig.2 Control structure of three-phase four-wire distribution network compensation device

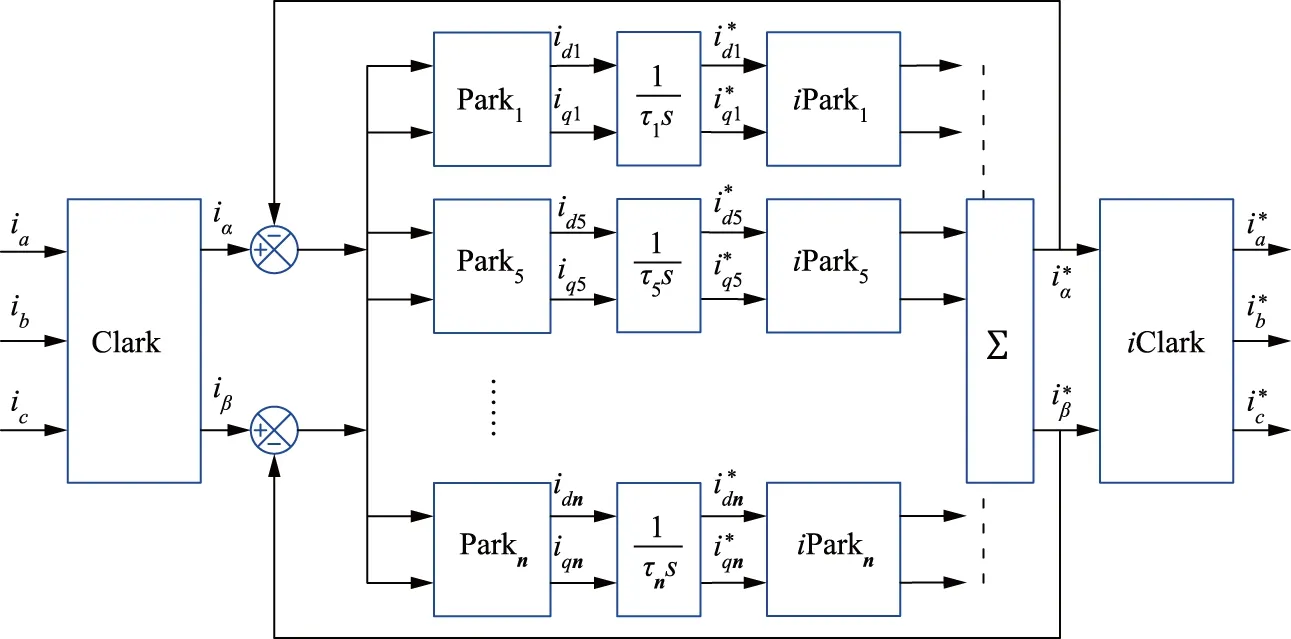
(a)正负序谐波检测结构

(b)零序谐波检测结构

图3 谐波分次检测算法总体结构

Fig.3 Overall structure of selective harmonic detection algorithm with different components

图4 基波正序分量检测传递函数频率特性图

针对零序谐波检测结构，在式(1)、(2)的定义下，可以求得第n次谐波检测开环传递函数为

(7)

系统总体开环传递函数为

(8)

由以上推导可以得出:在正、负、零序谐波检测的频率次数均相同时，零序谐波检测环节与正负序谐波检测环节的开环传递函数形式是一致的；因此在同等时间常数下二者特性也是一致的，可以直接选取正负序谐波检测控制参数用于零序谐波检测。

图5给出了基波无功峰值为50 A、5次谐波峰值20 A负载电流下的谐波检测结果。I+1d、I+1q、I-5d、I-5q分别为基波正序和5次谐波负序的d、q分量。其中：曲线①为本文采用的谐波检测算法计算结果，曲线②为传统多同步旋转坐标谐波检测算法计算结果，2种算法采用相同的时间常数。由图5可知，在相同的响应速度下，本文采用的谐波检测算法具有更小的稳态误差，证明其具有更好的实用性。

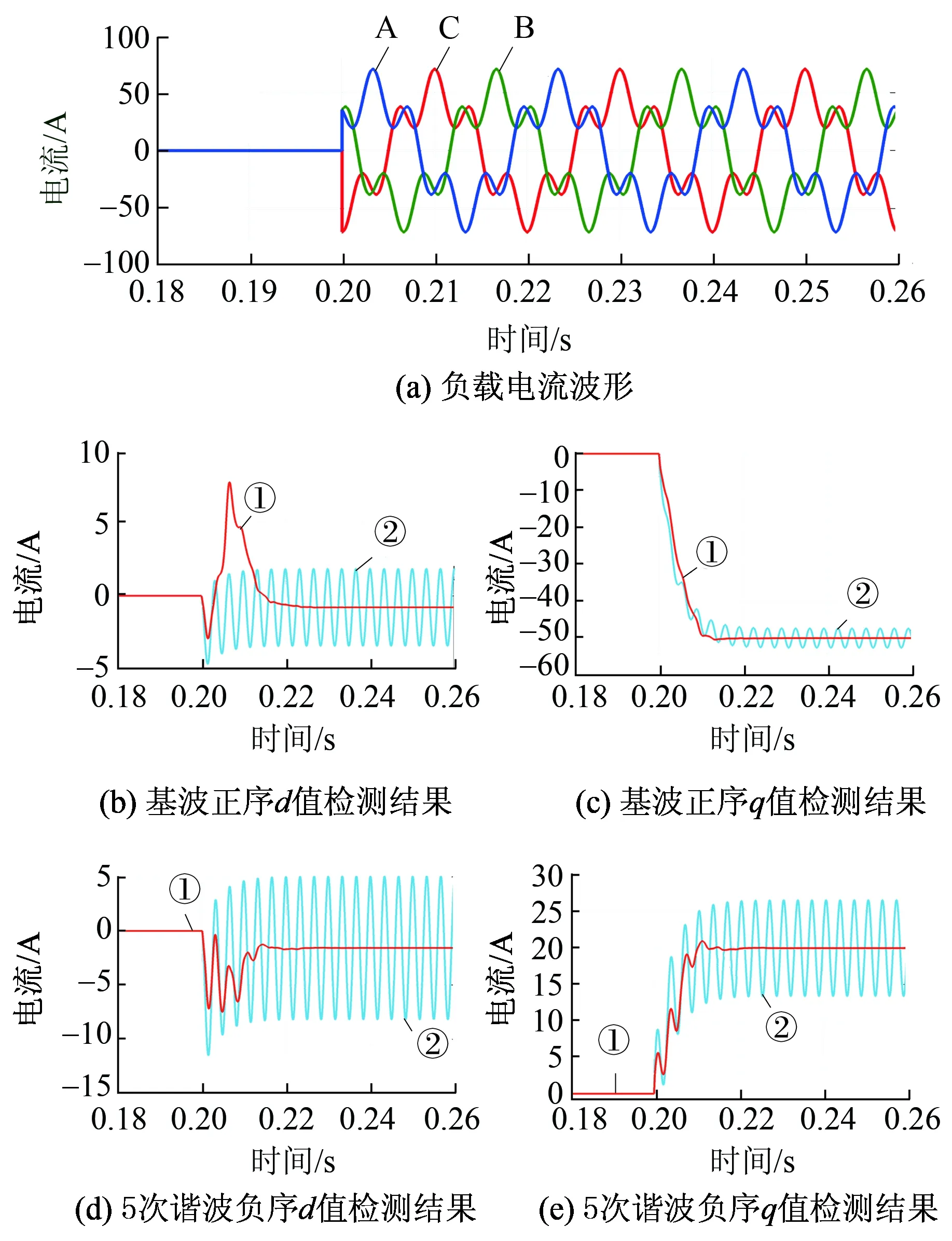
图5 改进谐波检测算法与传统算法效果对比

3 重复控制算法分析与设计

分裂电容式三相四线制中，三相之间是相互解耦的，因此可以把三相系统当作3个单相系统进行控制。重复控制对于周期性信号具有无静差跟踪能力，且相比多路谐波控制器而言具有节省计算资源、方便参数设计等优点；因此可以采用三路重复控制以实现基波和谐波电流指令的跟踪。重复控制器基本原理如图6所示。图6中:Gre(z)为重复控制器传递函数，Gc(z)为比例积分控制器；R(z)、Y(z)分别为系统的输入、输出；S(z)、Q(z)分别为补偿环节、低通滤波器；G(z)系统固有模块；z为Z变换量；N为延迟拍数。

图6 实际重复控制器基本原理框图

由图6可得重复控制器传递函数

(9)

应用于串联型复合控制器时，系统闭环传递函数为

(10)

式中Gcp(z)为重复控制器等效控制对象传递函数，且

(11)

系统特征方程为

F(z)=1-(Q(z)-S(z)Gcp(z))z-N=

1-Fre(z)z-N=0.

(12)

其中Fre(z)=Q(z)-S(z)Gcp(z)，当|Fre(z)|<1时，特征方程的根落在单位圆内，系统稳定。故在设计重复控制器时，需根据稳定性判据选取合适的补偿环节和内模系数。

常用的复合控制器为PI-重复控制器。考虑应用PI-重复控制器对桥臂电流进行控制，在PI输出处加入1拍滞后以模拟程序计算延时，于是有：

(13)

(14)

式中：GLCL为LCL滤波器传递函数；Ts为时间调节系数；Z()为Z变换;kp、ki分别为比例、积分系数；Kpwm为脉冲宽度调节系数。

首先对PI等效内环进行分析。设LCL滤波器参数为L1=120 μH，L2=20 μH，Cf=6.8 μF，Rc=2 Ω，采样频率fs=20 kHz，选择合适的PI参数(kp=0.002，ki=1.0)，绘制PI等效内环传递函数频率特性如图7所示。

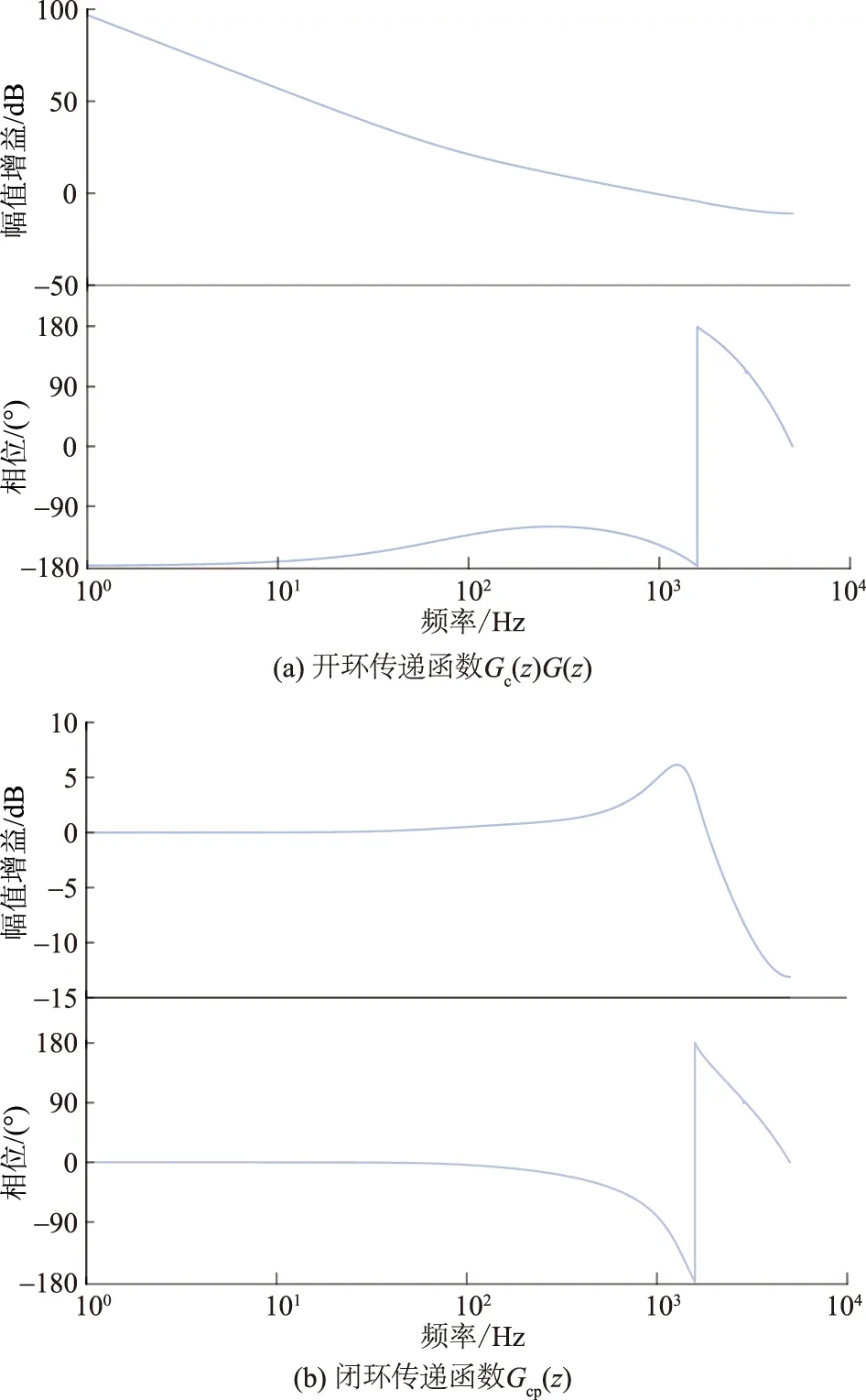
图7 PI等效内环传递函数频率特性曲线图

由图7可见：作为重复控制的等效控制对象的系统闭环传递函数在1 ～2 kHz之间存在较大增益，需要进行增益衰减；同时，系统闭环传递函数在半开关频率范围内存在360°相位滞后，需要加2拍超前相位校正，故选取补偿环节

(15)

该补偿环节在采样频率为1.67 kHz处增益为0，可以有效衰减控制对象的幅值增益。同理，选取内模系数为低通滤波器以减小高频衰减，低通滤波器

Q(z)=0.98+0.02z-1.

(16)

为了检验上述设计的合理性，绘制Q(z)、S(z)G(z)和Fre(z)的频率特性如图8所示。由图8可知系统是稳定的。

由于实际运行时电网频率存在波动，故求得的延时拍数将为非整数，为了提高复合的控制器的频率适应性，实现无静差跟踪，需要对延时拍数的小数部分进行模拟。设此时所需延时拍数为Ni，将其分解为整数和小数部分，即

图8 重复控制器各环节频率特性曲线图

Ni=Ni1+Ni2.

(17)

式中：Ni1为整数拍；Ni2为小数拍。一种常用的小数拍近似方法为[19]

Qn(z)=(1-Ni2)+Ni2z-1.

(18)

此时重复控制器表达式为

(19)

可以验证，在前述设计上加入小数拍模拟后系统仍然保持稳定，且加入近似后的复合控制器在频率波动时仍能保持较好的谐波跟踪能力，具有较好的频率适应性。

4 仿真和实验验证

为了验证上述设计的可靠性，在MATLAB/Simulink平台搭建了仿真模型进行了仿真验证。仿真涉及的基本电气参数如下：电网电压为220 V，电网频率为50 Hz，直流母线电压为785 V，开关频率为10 kHz，采样频率为20 kHz。LCL滤波器参数如下：逆变侧电感为120 μH，网侧电感为20 μH，滤波电容为6.8 μF，无源阻尼电阻为2 Ω。此外，滤波电容支路并联了谐振频率为10 kHz和20 kHz的LC支路，用于开关次纹波电流旁路。

考虑对如下不同的三相负载进行并联补偿：①三相无功负载，其中感性无功电流峰值为100 A；②三相不对称负载RLA、RLB、RLC，其中RLA=5 Ω，RLB=2 Ω，RLC=10 Ω；③三相不控整流负载，其中负载RL=5 Ω。针对这3类负载的并联补偿仿真结果如图9所示。三相不控整流负载补偿前后快速傅里叶变换(fast Fourier transform,FFT)后结果对比如图10所示。

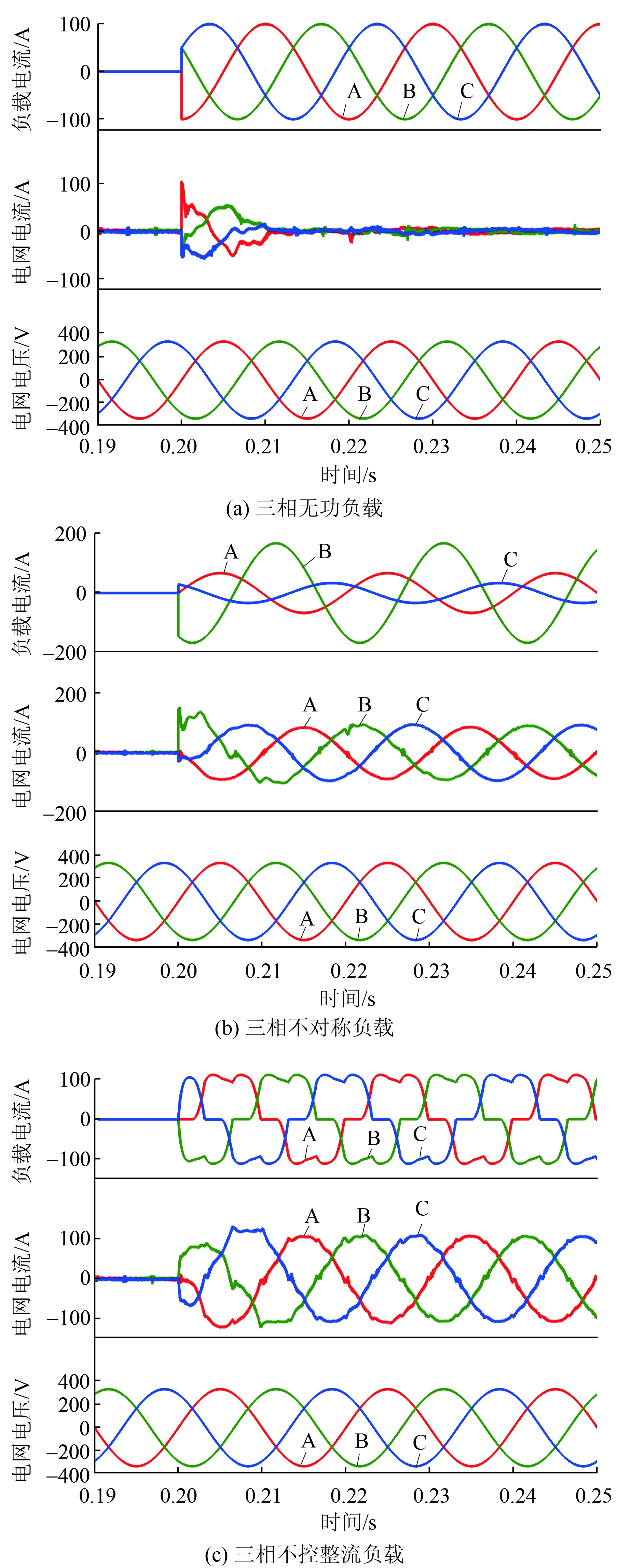
图9 不同负载的并联补偿仿真结果

由图9可知：针对三相无功负载，并联补偿后并网电流基本为零，即在补偿容量范围内没有无功电流进入电网；在切入无功负载的1个工频周期内，并网电流由于补偿迅速减小，具有较快的动态响应速度，且没有明显的电流过冲。针对三相不平衡和三相不控整流负载，负载电流存在不平衡或畸变，而并网电流在补偿达到稳态时为三相对称的正弦电流。

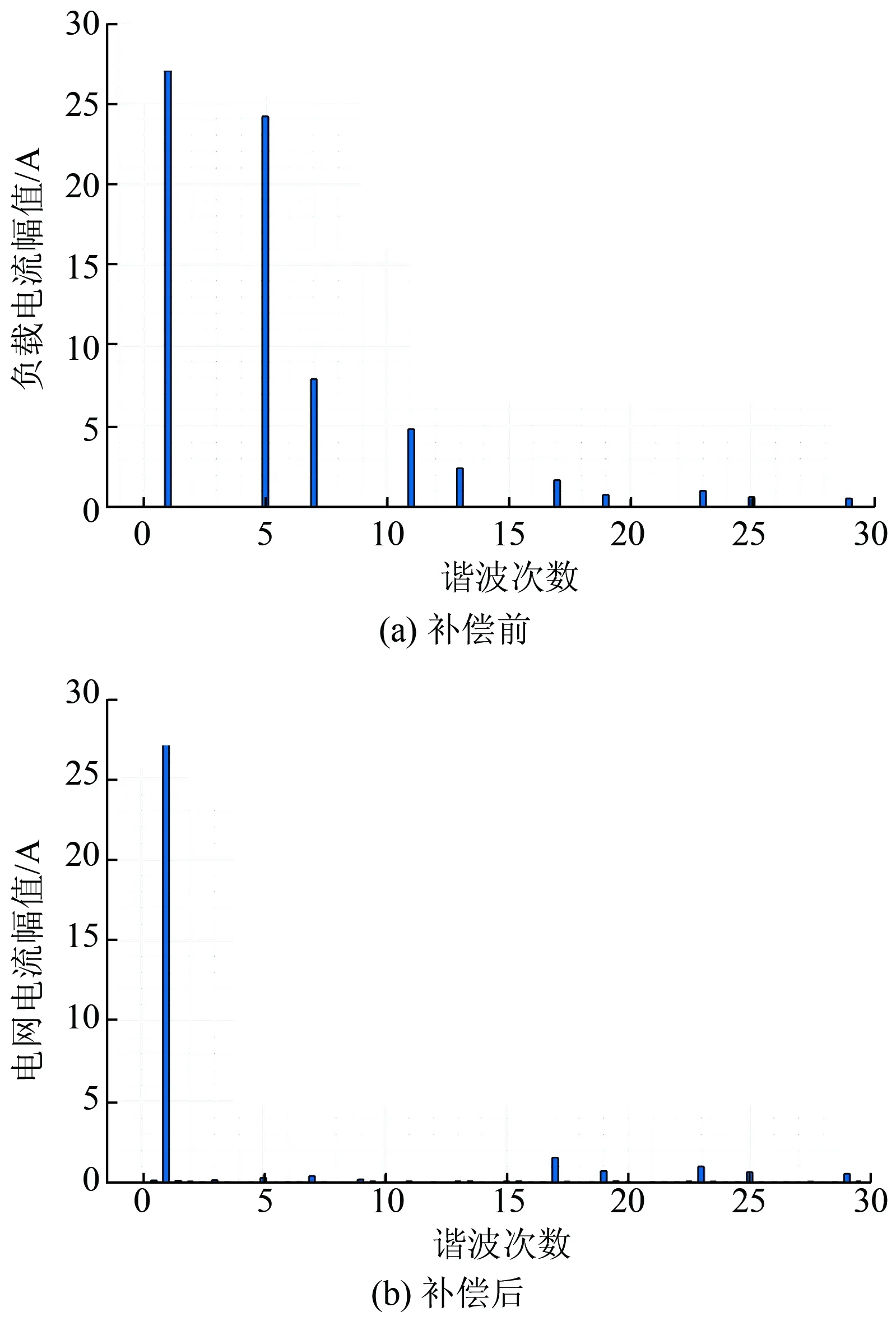
图10 三相不控整流负载补偿前后FFT结果对比

图10中，在未进行谐波补偿时，电网电流等于负载电流；进行谐波补偿之后，电网电流中的谐波成分由补偿装置进行抵消，因此可以统一为电网电流。图10中补偿前总谐波畸变率和基波幅值分别为22.84%和114.4 A;补偿后总谐波畸变率和基波幅值分别为3.44%和109.5 A，即补偿后的并网电流总谐波畸变率相比补偿前明显降低，其中5、7、11、13次谐波电流基本为零。由此证明了本文提出的补偿算法能够有效地补偿无功、谐波和不平衡电流，而且谐波可以选择性补偿指定的次数，从而使系统具有更高的灵活性。

为了实际验证前述设计的可靠性，制作了1台额定容量为100 kVA的三相四线实验装置，装置相关电气参数与仿真一致。图11给出了装置在额定条件下的三相感性无功电流并网实验波形，其中电流参考值峰值为150 A，实际有效值约为103 A，与给定电流一致。由图11可知，在给定电流参考条件下装置能够可靠运行，且电流波形质量较好。

图11 三相感性无功电流并网实验波形

图12给出了装置在不同负载下的补偿实验波形。其中三相无功负载为基波容性无功电流，其峰值为215 A。三相混合负载为基波容性无功电流叠加5次负序谐波电流，基波电流峰值为100 A，谐波电流峰值为40 A。由图12可知，在不同负载条件下，补偿装置均能够精确地跟踪负载电流，实现有效的无功及谐波补偿功能。

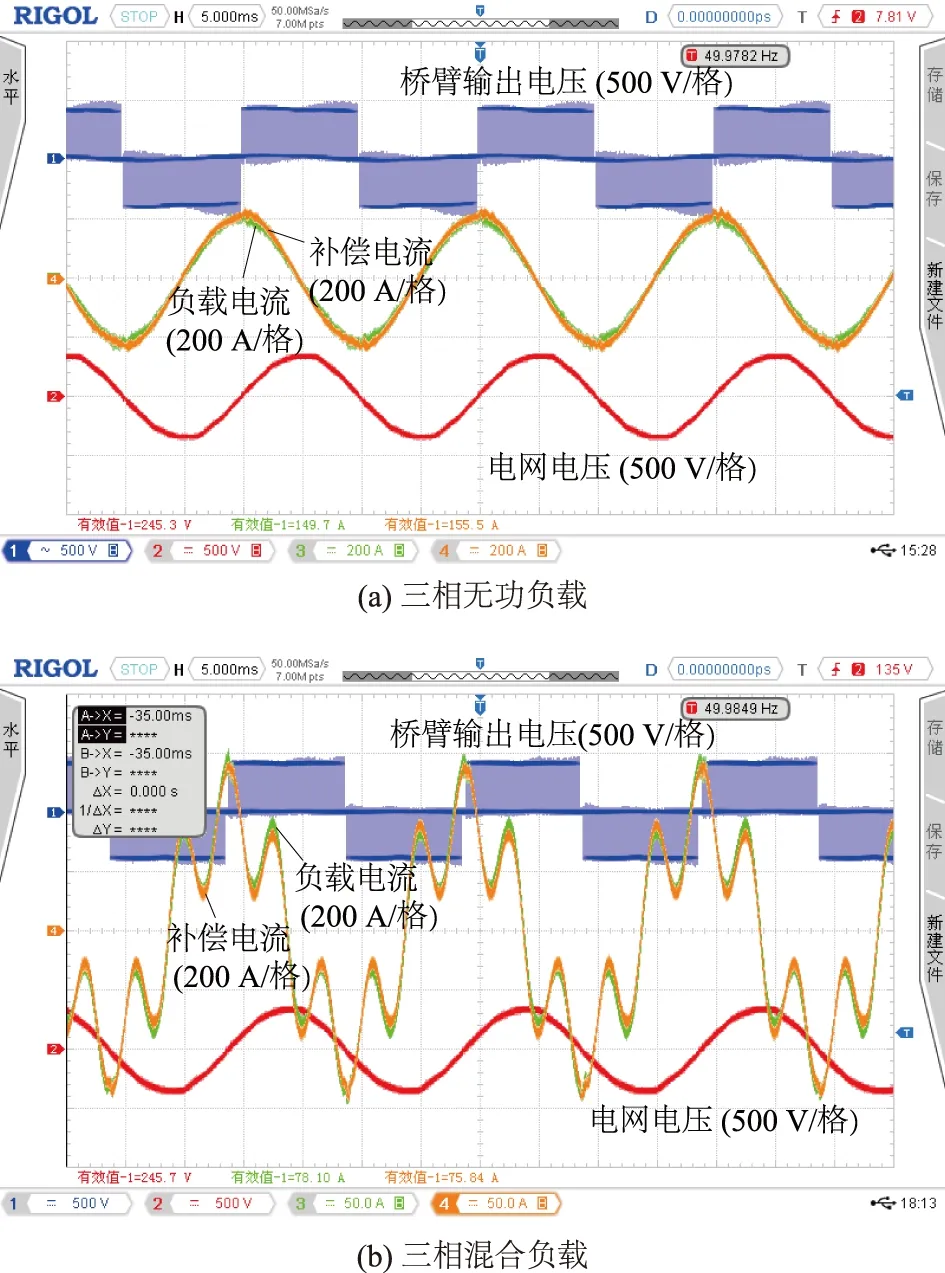
图12 不同负载下补偿实验波形

5 结束语

本文提出一种基于谐波分次检测与重复控制算法的三相四线制配电网电能治理装置控制方案。其中谐波分次检测采用改进的多同步旋转坐标变换谐波检测法，相比传统检测法具有更高的检测精度。重复控制算法能够对给定的基波和谐波电流指令实现无静差跟踪，实现简单且占用资源少。仿真结果验证了该算法的有效性，并说明了本文提出的控制方案具有较低的补偿误差和较高的动态响应速度，适用于无功、谐波和不平衡多种负载补偿场合，具有较高的实用性。