二维数学模型在某亲水广场防洪评估中的应用
2020-06-04石少山
石少山
(重庆交通大学 河海学院,重庆 400074)
河道内建筑物侵占部分过水断面,减小了行洪面积,一般水位会因此产生一定的壅高,抬高防洪实际水位,存在阻挡河道行洪的风险,给防洪抢险带来较大的难度和危险。其次会改变水流的运动形态和速度大小,打破最初河道内已经形成的局部冲淤平衡状态,冲刷原有的岸坡和改变深泓线的位置,逐渐改变河道的走向、形态直至到达新的平衡点[1]。大部分学者研究的是大型跨河建筑物和山区大洪水规模下对河道防洪的影响,但对于平原流域小规模涉水建筑物研究甚少。例如:张细兵[2]等通过simple算法建立了二维水流模型,利用桥墩局部地形修正和局部糙率修正,针对井冈山阳明大桥桥渡壅水问题进行了分析。李大鸣[3]等通过集中质量的有限元方法建立数学模型,模拟天津至保定新建铁路特大桥梁对水流的阻碍作用和局部冲刷深度。张大茹[4]等利用Mike 21HD软件,模拟分析了以北京房山区红螺谷小流域为代表的山区大小桥梁、漫水桥等对防洪的影响。因此广东某小流域亲水广场建设前对方案的模拟预测,分析出方案的合理性和可能存在的问题评估是必要的[5-6]。文章采用二维数学模型[7-8],为某亲水广场防洪影响提供理论支撑。
1 工程概况
某河道全长13.5 km,流域面积为129.4 km2,梯形河槽,宽约51 m,河底高程为34.2 m。百年一遇洪水位为39.06 m。拟建亲水平台位于河道右岸,平面采用顺岸式布置,左右两岸为居民区,亲水广场总长约138 m,宽约24 m,广场二级平台高程为41.25 m,一级平台高程为41.70 m,广场平台伸出堤岸,位于岸坡之上,其下端用23根直径1 m的圆柱形支柱支撑,沿水流流向分为两排,部分支柱沿岸坡布设于坡身位置处,其余支柱沿岸坡布置于坡顶附近位置(见图1)。

图1 广场剖面示意
2 平面二维数学模型的建立
2.1 基本方程
二维数学模型的控制方程是基于对不可压缩流体的三维雷诺 Navier-Stokes平均方程沿水深积分的水流连续性方程和动量方程,通过有限体积法求解方程组[9],进而得到任一点的流速、水深、流向等相关计算结果。笛卡尔坐标系方程表示如下:
水流连续性方程:
(1)
水流动量方程:
(2)
(3)
式中ζ为水面高程;d为时变水深;h(h=ζ-d)为水深;p,q分别为x,y方向的单宽流量;C为谢才系数;f为风阻力系数;V为风速,Vx,Vy分别为风速在x,y方向的分量;Ω为科氏力参数;Pa为大气压强;τxx,τxy,τyy为各方向的有效切应力。
2.2 模型网格剖分
河道横断面整体较规则,断面呈梯形,纵向较为顺直,地形数据来自该河道综合整治后地形数据。为减小工程上下游附近河道对研究区域的影响,保证水流进出口呈稳定状态,上游边界取距离亲水广场上边界150 m,下游边界取距离亲水广场下边界120 m。故计算区域河道面积约为19.9 km2,全长约410 m。模型采用非结构三角形网格,本工程中考虑影响水流的因素是广场下支柱,为提高计算精度,对重点研究区域即支柱附近进行网格加密,保证模型计算精度,如图2。通过局部高程修正对工程支柱进行概化[10],其目的是为模拟工程现场因支柱的存在使过水断面减小的工况。网格数量6 142个,节点3 250个,最大网格面积10 m2,最小三角形角度为26°。
2.3 模型参数设置
广场位于小流域未设置水文观测站,但有一个雨量站,保留观测数据从1961年至今。根据水利水电水文工程相关规范并结合该河已有干流综合整治工程中计算结果,推求广场上下游设计洪水和设计水位。百年一遇工况下(该河防洪标准为P=1%),上游边界条件为设计流量493.3 m3/s,下游边界条件为设计洪水位38.63 m。为满足模型稳定启动,初始条件设定值与洪水位相近。经验证模型的糙率值为0.0182。
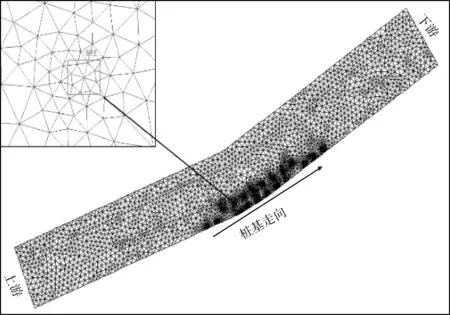
图2 计算网格示意
2.4 模型验证
二维模型验证水文条件选择广场上下游间隔100 m的5个断面实测水位(见图3所示),与模拟结果比较进行验证,水位对比见表1。
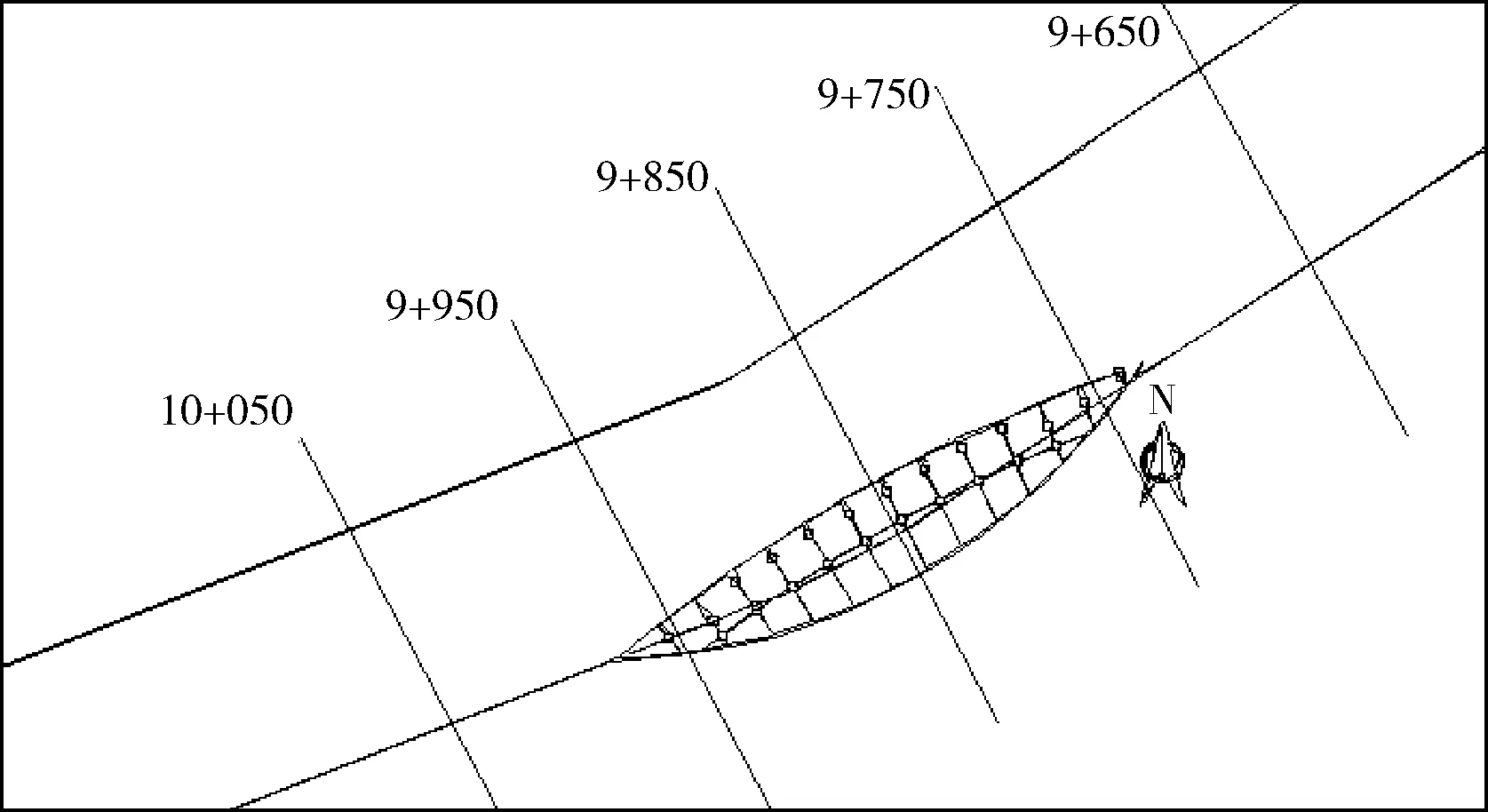
图3 实测水位断面示意
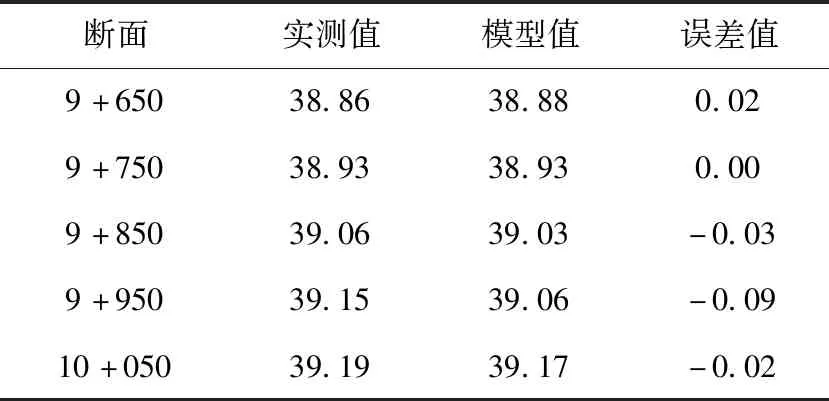
表1 二维模型水位与实测值 m
3 模型计算结果分析
3.1 壅水分析
为分析壅水变化,在广场上下游布置了4个水位测量断面(如图4所示),序号为1、2、3、4。此工程类似桥梁墩对水流的影响,根据张利[11]等学者的研究,建桥后桥上游水位产生壅水,桥下游水位产生跌水。但本工程在100年一遇的设计水位条件下:工程前后洪水水位略有降低(见表2),其主要原因是虽然广场工程支柱阻水面积为10.25 m2,但由于工程段岸坡开挖,河道内右岸断面面积工程后比工程前共增加了5.22 m2。因此工程处断面水位最大降低值为0.03 m,其他断面基本不变。结果表明在河道行洪时水位不会超过原设计河道洪水水位,满足防洪度汛要求。

图4 水位测量断面示意
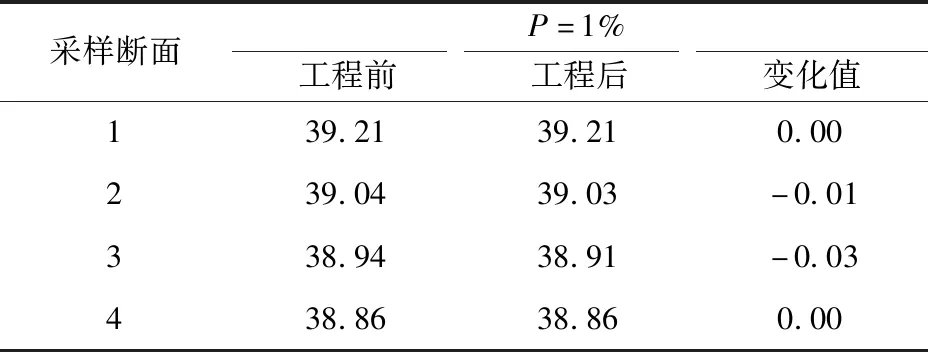
表2 工程前后洪水水位变化成果统计 m
3.2 流向分析
在模型概化范围内均匀布置了40个流速采样点(如图5所示),从相同位置支柱的工程前流场(见图6)和工程后流场(见图7)知,工程后流场相对于工程前流场流向发生偏转,角度在5°以内,其原因是水流方向因广场支柱的阻挡发生了偏转。但流向改变影响范围和偏转角度仅存在于局部,不会对河道整体走向产生影响。整体看水流流向与河道岸坡平行且顺直,在广场支柱附近流向变化且在0.5 m范围内,研究区域对整体河道影响有限,满足水流与地方岸线平行要求。工程后全局流场如图8所示。
3.3 流速分析
从工程前后流速等值线(见图9)知,在100年一遇水文组合条件下,流速变化规律为:右岸工程桩基上下游一定范围内因受到广场支柱阻碍流速整体减小,工程附近水域流速最大减小值为0.8 m/s。其河道左岸水域因过水断面减小而有所增加,左岸流速增加为0.2 m/s,增加后流速最大值为3.5 m/s。原有河道护坡采用WE渗滤砌块和六角生态砌块,河底护角采用钢筋石笼和大块石护脚。根据《堤防工程设计规范》[12]岸坡能抵抗洪水冲刷。流速变化对河道岸坡影响产生的冲刷强度有限。

图5 流速采样点示意

图6工程前流场示意

图7 工程后流场示意
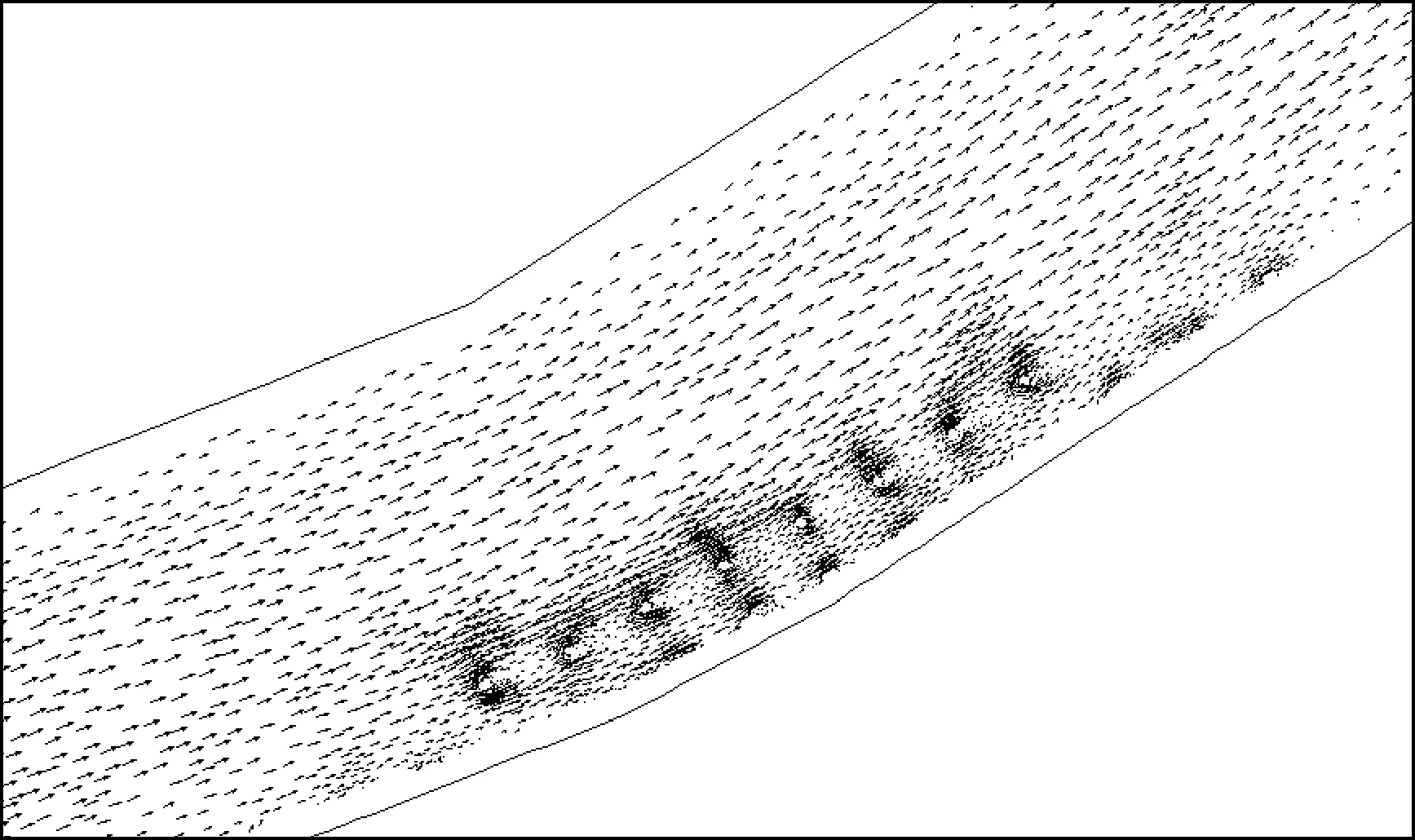
图8 工程后全局流场示意
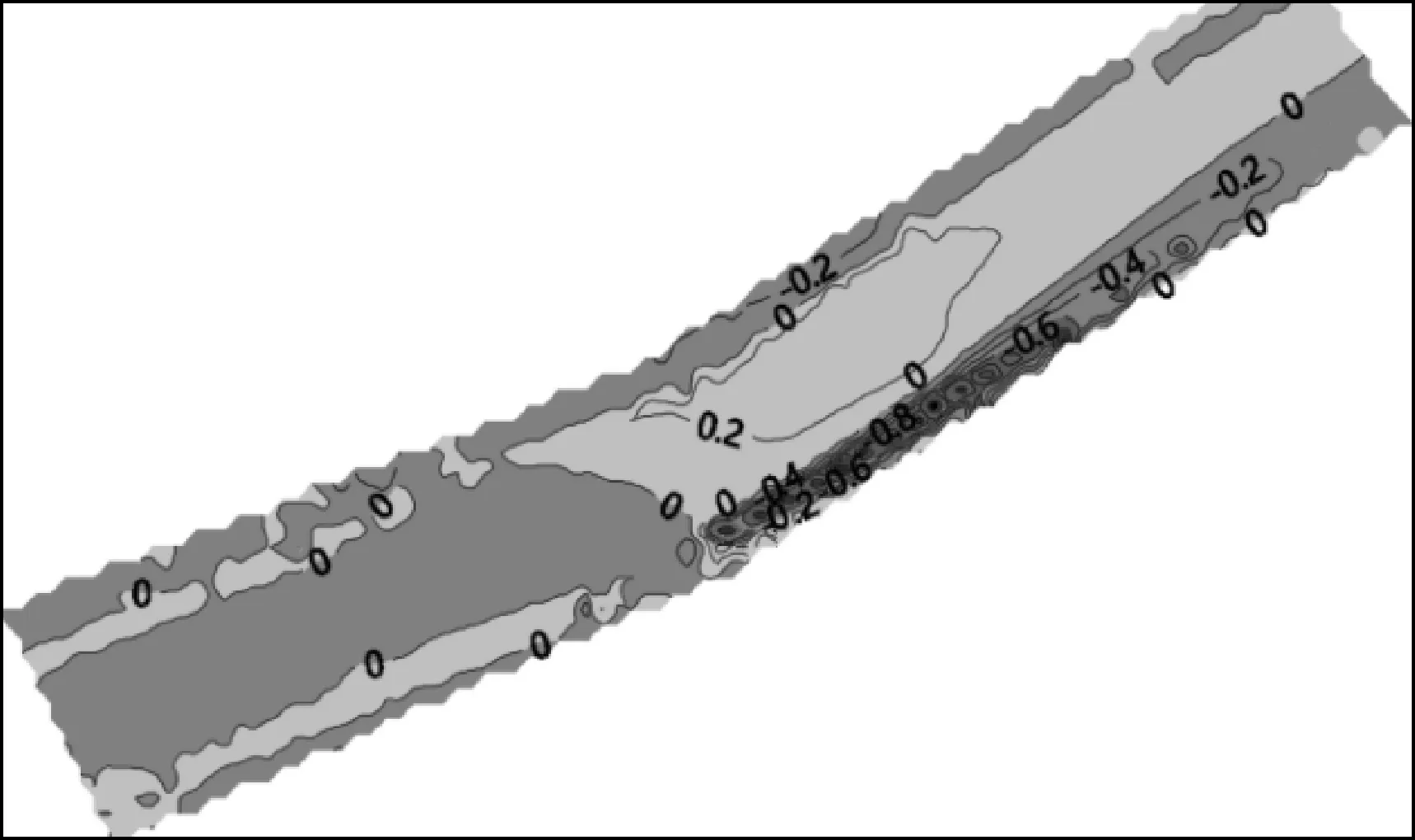
图9 工程前后流速等值线示意(m/s)
3.4 水动力轴线分析
由工程前后的水流动力轴线(见图10)知,从横向看,水动力轴线相对于工程建设前略微向河道左岸产生了偏移,偏移量约为2 m,占河道总宽的0.04,且河道底部经整治后为近似水平,无需对岸坡进行特殊处理。从纵向看,水动力轴线偏移位置仅发生在工程建设附近,在工程建设上游和下游水动力轴线均未发生明显偏移。冲淤现象因流速变化小而不明显。
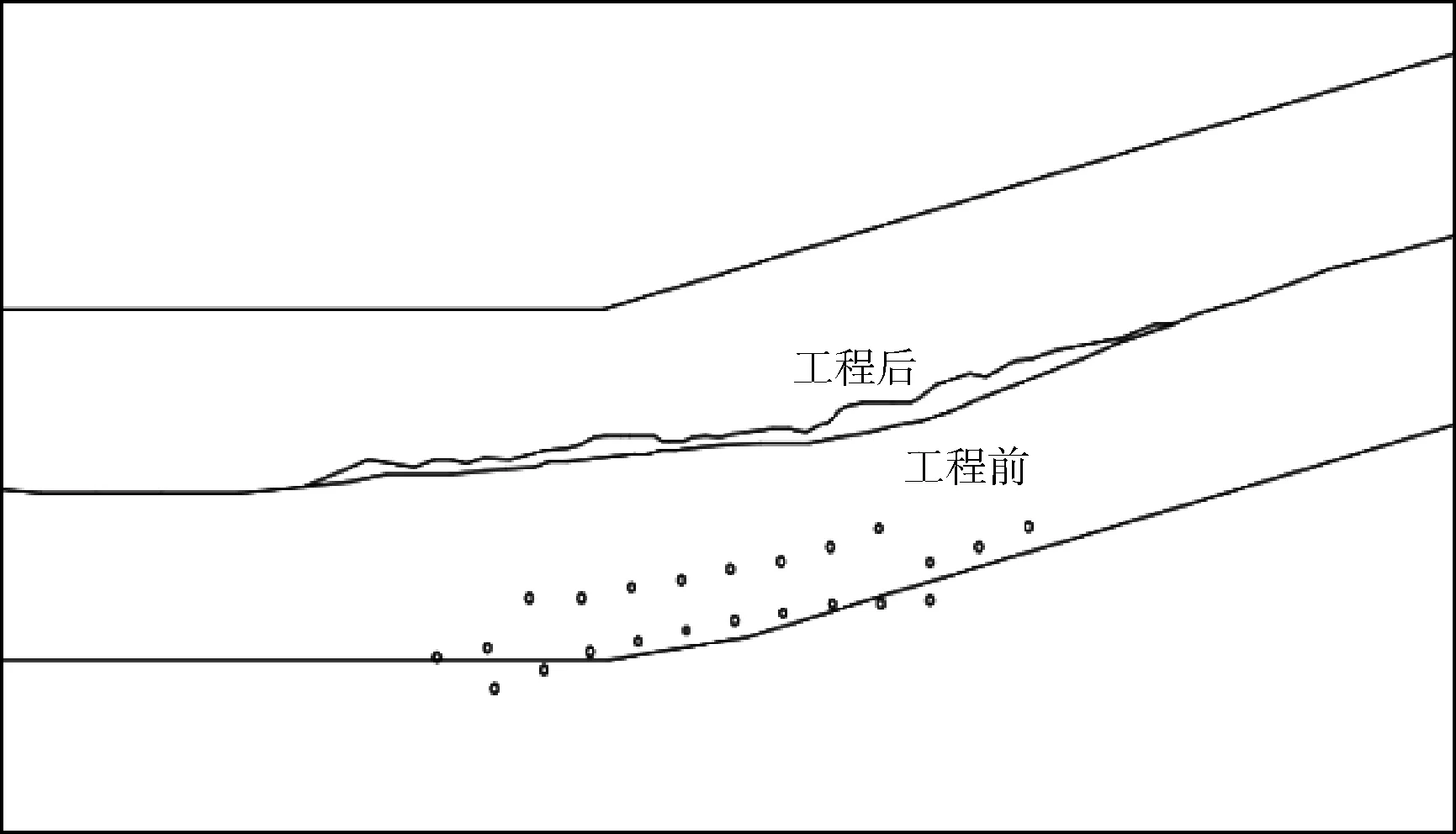
图10 工程前后水动力轴线示意
4 结语
本文通过建立某亲水广场平面二维水流数学模型,经验证模型能够模拟分析新建亲水广场对河道水流的影响。总体而言,二维数学模型能较准确模拟工程,模拟结果显示广场桩柱修建不会对河道产生较大影响,仅在局部范围内发生变化,符合河道防洪安全标准。
