不确定性最小二乘估计及其统计性质

王志忠 邹航

(中南大学数学与统计学院,长沙,410083)

1 引言

线性模型在现代统计学中一直受到广泛关注，其中，参数估计是研究领域中的热点问题，最早由Legendre和Gauss[1]提出最小二乘估计，并应用到观测数据中.在实际问题中对变量进行观测时，得到的观测数据通常带有测量误差，这在早期由R.J Adcock进行了研究[2].在线性回归模型中，经典的最小二乘法只考虑因变量存在误差，但实际上模型中自变量同样存在一定误差[3].这些误差带有不确定性，有时是一个明确的数值，有时在一定的实数区间内变动，有时仅是概念上的模糊数[4]，且包含先验信息.对于不确定性先验信息，在线性回归模型中的一种有效解决方法是添加惩罚项，也就是约束条件[5], 合理地将之以等式约束、不等式约束或区间约束的形式融入模型中，以有效改善参数估计结果[6-9].

文献[10]首先研究了不等式约束的回归分析.杨婷，杨虎[11]针对设计矩阵的病态问题，考虑了回归系数的椭球约束，得出了椭球约束下线性模型参数的广义岭型估计.刘朝林等[12]讨论了线性模型在随机约束下的参数估计问题，提出了几乎无偏加权混合岭估计，并证明了它的优良性质.张二艳等[13]基于广义逆矩阵理论，推导了矩阵解法，把多个约束条件的参数估计问题转化为无条件极值问题.

最近有许多学者研究了一种新的不确定性，“未知但有界(unknown-but-bound,UBB)的噪声”[14-16]，这在大地测量领域中受到了广泛关注.针对UBB噪声，Fogel 等在提出集员估计方法的基础上[17]，用椭球形式描述参数的可行集，提出了相应的椭球集员估计[18].黄一等[19]提出了一种避免椭球相交计算的最小迹扩展集员估计.基于用椭球集合对有界不确定性进行描述这种思想，宋迎春[20]利用观测向量和参数的两个椭球集合的交集来描述不确定性，建立椭球不确定性线性模型，在外接椭球特征矩阵的迹最小化准则下求得最优二乘解，解算过程十分复杂.为了优化解算过程，提高椭球不确定性回归模型的可靠性，本文采用直接迭代算法求解椭球约束线性回归模型，得到参数的加权估计，并研究权值分配对参数估计的影响，进一步讨论估计的可容许性.

2 不确定性最小二乘估计

考虑不确定性线性回归模型：

L=AX+e，e～N(0,P)，

(1)

其中，A为m×n(m≥n)维设计矩阵，且列满秩，L为n维观测向量，X=(x1,x2,…,xn)T为n维参数向量，e为m维有界观测误差.

误差有界不确定性由椭球约束描述：

E(e)={e:eTP-1e≤1}={X:(L-AX)TP-1(L-AX)≤1}.

(2)

式(2)表示观测值先验信息约束，或样本先验信息约束[20].观测值L的先验均值为E(L)=AX.取X0使得L=AX0，则椭球约束(2)可表示为

E(e)={X:(X-X0)TATP-1A(X-X0)≤1}，

(3)

其中，X0=XLS=(ATA)-1ATL.

由文献[20]知，未知量X的不确定性可由椭球约束描述，即X的先验信息描述为：

E(c,Q)={X:(X-c)TQ-1(X-c)≤1}，

(4)

其中，c为未知量X的先验均值，Q为X的先验方差.

文献[20]中的式(14)给出了带有椭球不确定性约束的参数估计：

(5)

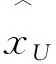
min (L-AX)TP-1(L-AX)，

s.t.X∈E(e)∩E(c，Q).

(6)

对上述带有椭球约束的参数估计问题，参照文献[22]，引入Lagrange乘子，结合Kuhn-Tucker条件，最小二乘准则(6)可写为

min(L-AX)TP-1(L-AX)+λ1(X-X0)TATP-1A(X-X0)+
λ2(X-c)TQ-1(X-c)，

(7)

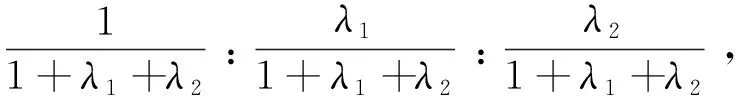
与文献[20]所得式(5)类似，通过对式(7)求解，得到不确定性最小二乘估计的解为

(8)

进一步，对式(8)变换得到

(9)

(10)

其中，X0=XLS=(ATA)-1ATL.

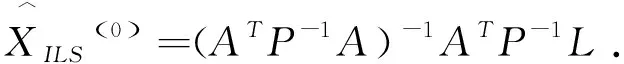
代入式(10)得

将得到的λ1(i+1)和λ2(i+1)代入式(8)得

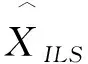
3 不确定性最小二乘估计的统计性质

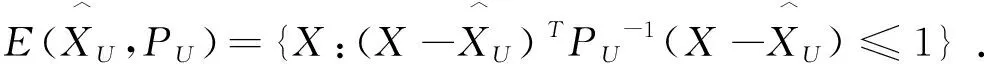
(11)

其中[20]，

(12)

引入Lagrange乘子，结合上述和Kuhn-Tucker条件，不确定性最小二乘准则(6)变为：

(13)

类似可以得到，不确定性最小二乘准则(13)的解为

(14)

(15)

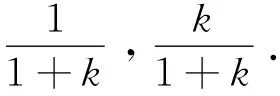
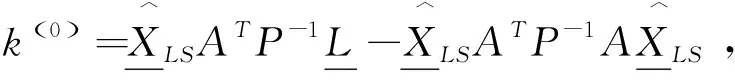
将得到的k(i+1)代入(14)式得

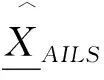
文中出现的三个估计，式(5)利用两个椭球交集的最小迹外包椭球建立最小二乘准则得到参数估计；式(8)针对带有两个椭球约束的线性模型引入Lagrange乘子，结合Kuhn-Tucher条件建立最小二乘准则求得参数估计；式(14)先求得两个椭球交集的最小迹外包椭球，在该外包椭球的约束下，引入Lagrange乘子，结合Kuhn-Tucher条件得到参数估计；式(8)利用两个椭球交集的最小迹外包椭球，将两个椭球约束转化为一个椭球约束，建立最小二乘准则估计参数得到式(14)，这样能更好地研究估计的性质.

下面来研究不确定性最小二乘估计的容许性.

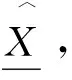
(16)

均方误差可分解为

(17)

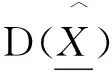
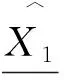
性质1不确定性广义岭估计(14)是有偏的[11][24].

椭球约束E(PU)可写为

(18)

其中PU-1=ATNA.

(1)C=CA(ATP-1A)-1ATP-1；

(2)CPNPCT+CPCT≤CA(ATP-1A)-1；

(3)tr{PNPCT(CA(ATP-1A)-1)-1CP[P-PCT(CA(ATP-1A)-1)-1CP]-1}≤1.

上述条件中矩阵逆不存在时，用广义逆替代.

证明为证明不确定性最小二乘估计的可容许性，将估计(14)式化为线性形式

(19)

由(19)知，C=(ATP-1A+kPU-1)-1ATP-1.

(1)将式(19)直接代入条件(1)，可知条件(1)成立.

(2)将式(19)代入条件(2)的左边有

CPNPCT+CPCT=(ATP-1A+kPU-1)-1PU-1(ATP-1A+kPU-1)
+(ATP-1A+kPU-1)-1ATP-1A(ATP-1A+kPU-1)
≤(ATP-1A+kPU-1)-1，

(20)

即

PU-1+ATPA≤ATP-1A+kPU-1，

(21)

化简得到k≥1.

(3)对于条件(3)，利用公式(F-CG-1D)-1=F-1+F-1C(G-DF-1C)-1DF-1可得，条件(3)的左边=tr{PNA(ATP-1A+kPU-1)-1AT[P-A(ATP-1A+kPU-1)-1AT]-1}=tr{PNA(ATP-1A+kPU-1)-1AT[P-1+P-1A(ATP-1A+kPU-1-ATP-1A)-1ATP-1]}=tr{PU-1(ATP-1A+kPU-1)-1+k-1PU-1(ATP-1A+kPU-1)ATP-1APU}=k-1tr{(ATP-1A+kPU-1)-1(kPU-1+ATPA)}=k-1P≤1，即k≥p.

综上，当p≤k时，估计(14)是容许估计.

4 实例分析

4.1 实例一

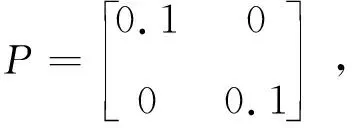
4.2 实例二

实验数据来源于文献[28]的测边网.在该测边网中，P1～P10是已知点，坐标如表1所示，k1，k2，k3是未知点，其坐标真值分别为(68，-26，9)，(14，41，-11)，(0，0，0)，3个未知点之间的观测距离分别为dM1M2=88.3402，dM1M3=73.3551，dM2M3=44.8901，已知点与未知点之间的观测距离在表1中给出.测边网如图1所示.

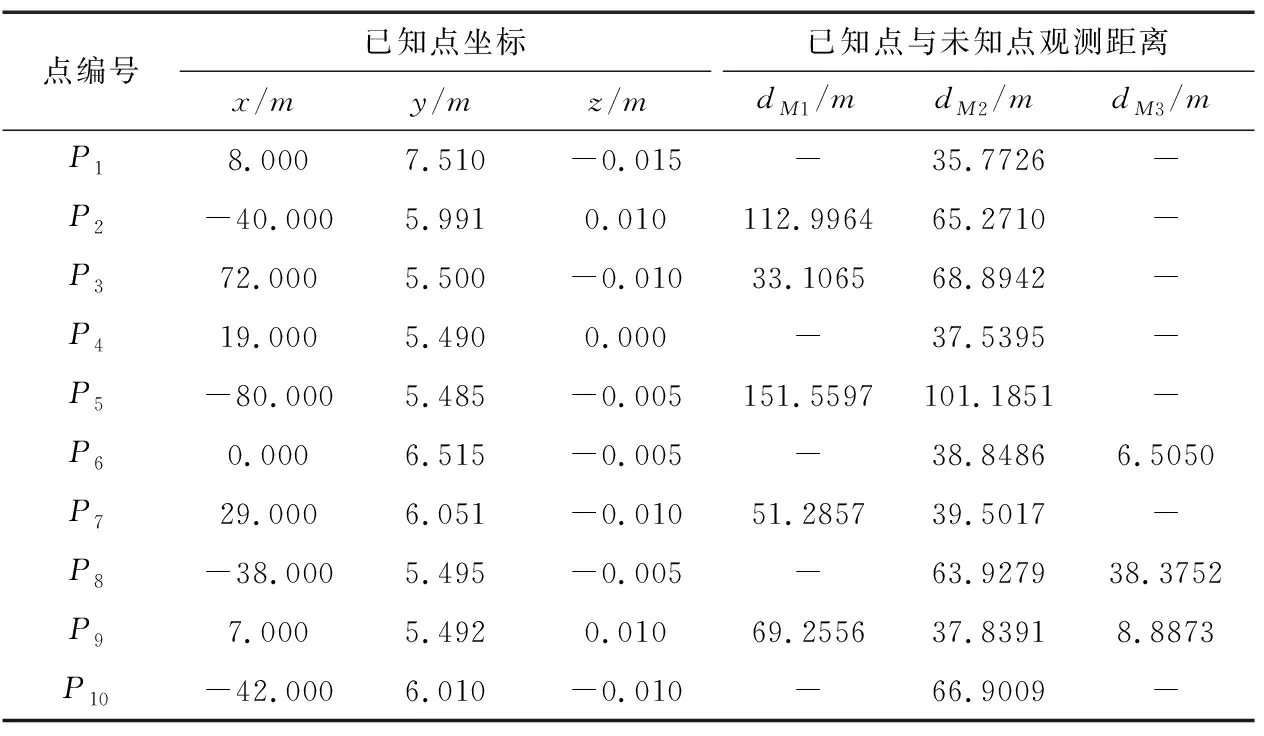
表1 已知点坐标和观测距离

图1 测边网

已知e～N(0,δ2I)，δ=0.01.取e∈[-0.2，0.2]，区间关于原点对称，则e的椭球特征集合为E(e)={e:eTP-1e≤1}，其中

P=diag(0.0088，0.0088，0.0088，0.0088，0.0088，0.0088，0.0088，0.0088，0.0088，0.0088，0.0088，0.0088，0.0088，0.0088，0.0088，0.0088，0.0088，0.0088，0.0088，0.0088，0.0088,0.0088).

对于3个未知点，近似坐标分别为(68.029，-26.010，9.019)，(14.040，40.860，-11.009)以及(0.02，-0.01，0.01)，近似坐标对应的点位精度分别为(0.029，0.01，0.019)，(0.04，0.14，0.009)以及(0.02，0.01，0.01).将2倍点位精度l作为参数下边界值，3倍点位误差u作为参数上边界值，即X∈(l，u)，其中l∈(-0.058，-0.02，-0.038，-0.08，-0.28，-0.018，-0.04，-0.02，-0.02)T，u∈(0.087，0.03，0.057，0.12，0.42，0.027，0.06，0.03，0.03)T，则

c=(0.0145，0.0050，0.0095，0.0200，0.0700，0.0045，0.0100，0.0050，0.0050)T，椭球特征矩阵为E(X)={X:(X-c)TQ-1(X-c)≤1}，其中

Q=diag(0.0473，0.0056，0.0203，0.0900，1.1025，0.0046，0.0225，0.0056，0.0056).

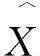
实验结果见表2，可以看出，系数矩阵呈现严重病态时，普通最小二乘解严重失真，对应的M值为7.0327；L曲线(岭估计法)有效地提高了解的可靠性，M值为0.1069；不等式约束(罚函数法)在经过3次迭代后，得到参数稳定解，M值为0.5493；相对于椭球约束，本文的直接迭代算法同样利用了点位误差范围提供的先验信息，是岭估计的一种推广，在经过10次迭代后，得到了更精确的估计值，M值仅为0.0294.

表2 不同方法参数估计比较结果

4.3 实证结果分析

(1)系数矩阵A呈现严重病态时，本文提出的直接迭代算法求解未知参数的估计和权重系数依然有效，相比处理病态模型的其它算法，如表2中的L曲线(岭估计法)，本文算法精度更高.不等式约束和椭球约束虽然也利用了先验信息，但计算结果依然不如本文算法.

(2)在岭估计的表达式中，λ1远小于λ2，说明椭球不确定性约束先验信息在参数估计中的作用更大.当模型出现病态时，利用参数先验信息可以改善病态性.

5 总结

在线性模型观测数据的获取过程中，通常含有随机误差，同时未知参数中，也存在难以度量的不确定性，这给参数估计和精度评定带来了困难.本文基于椭球不确定性线性模型，提出了直接迭代求解算法，解决了观测样本信息和先验信息权重分配问题，从权重计算结果看，参数约束先验信息在参数估计中的作用更大.当系数矩阵呈现严重病态时，有效利用参数先验信息，可以提高估计的可靠性.最后，本文提出了椭球不确定性最小二乘估计是容许估计的充要条件，研究了估计的统计性质.