一种基于光纤激光水听器的PGC改进解调算法

冉艳丽，倪晶利，傅润秋，刘德明

（1.深圳大学 微纳光电子学研究院，广东 深圳 518060；2.深圳华中科技大学研究院 NGIA 深圳分室，广东 深圳 518060）

引言

光纤水听器[1-2]传感与传输介质均为光纤本身，它能高灵敏地探测水下微弱声场信号，可实现目标探测、海洋环境监测等功能。由于低频声波在水中传输损耗小、传播距离远，因此光纤水听器可以探测较远距离的目标。

自20世纪70年代以来，基于光纤水听器被认为是目前传统压电声学传感器的替代品，在许多国家受到了广泛关注。光纤水听器在尺寸、可靠性、抗电磁干扰和电无源传感方面具有优势，被用于监测其它船只和潜艇。在民用领域，它们广泛应用于石油、天然气井测量和地震分析中[3-4]。

光纤水听器按照工作原理可分为强度型、干涉型和波长型3 种[5]。强度型光纤水听器基于光强在传输过程中受声信号影响产生变化的原理实现外界探测，常用结构包括光纤微弯、受抑全内反射和光纤绞合等。该类光纤水听器有光路设计简单易于实现的优势，但这些因素同时制约了该类水听器的动态范围和噪声性能，且其灵敏度更多取决于探头的结构设计与加工水准。干涉型光纤水听器在光路设计上采用典型干涉仪模型，探测端声压作用使光程发生变化，从而影响干涉光的相位。目前发展较为成熟的是迈克尔逊和马赫-曾德干涉型光纤水听器[6]。该类水听器相比于强度型水听器在探测灵敏度、动态范围、噪声性能等诸多方面有一定优势，同时解调方法、光路设计等也更加复杂。随着光敏光刻技术的发展，布拉格光栅技术得以应用在光纤上。波长型光纤水听器多依赖各类光纤光栅（布拉格光栅、长周期光栅、相移光栅等）对波长的调制作用，声波会使光栅对中心波长的选择位置产生变动，通过检测波长的变化即可获取声波的相关信息。布拉格光纤光栅水听器以其体积小、成本低、易于成阵等优点，成为了各国研究的热门技术[7]。

最早出现的光纤光栅水听器是无源型光栅水听器，但由于受到光栅信噪比的影响，其发展及应用受到制约。随着光栅刻写技术的不断成熟和光纤掺杂技术的发展，分布反馈式（distributed feedback，DFB）光纤激光水听器逐渐呈现在人们的视野中。DFB 光纤激光水听器是有源型光栅水听器，它是在掺铒或掺镱光纤中刻有λ/4 相移光栅或λ/2 相移光栅（如图1所示），即在布拉格光栅的中间形成一个间距为λ/4 或λ/2 相移作为光纤激光器谐振腔[8]。这种相移光栅可以保证光纤激光器单模输出，形成更窄的透射峰。相比较无源型光纤光栅水听器，其功率更高，反射波长更窄，更易于成阵发展。

图1 相移光纤光栅结构示意图Fig.1 Schematic diagram of phase shift fiber grating structure

2008年，张文涛等[9-10]首次提出基于双膜片结构的光纤激光水听器。当外界声压作用在基元表面上就会使两端的膜片反向变形，从而拉伸光纤激光器产生增敏应变。2011年，Zhang F X 等[11]提出了一种具有低通滤波功能的光纤激光水听器，它是在膜片式光纤激光水听器基础上添加了低通滤波结构实现的频响变换。2018年，唐波等[12]研究出一种聚氨酯端面增敏结构的DFB 光纤激光水听器，并建立该结构的理论模型，分析了套筒结构与加速度灵敏度关系，进而优化水听器的结构及材料参数。

虽然光纤激光水听器有着体积小、成本低、易于成阵的优势，但由相比于强度型和干涉型光纤水听器，光纤激光水听器探测的声信息搭载在更微弱的激励光中。因而为了提升其性能，一方面可以优化水听器基元的设计，另一方面可以优化相应的解调算法。目前对DFB 光纤激光水听器的研究大多都是基于基元结构设计，而对信号处理系统的研究较少，使用的解调方法往往与干涉型水听器近似。

信号解调是水听器系统实现的重要部分。相位生成载波（phase generated carrier，PGC）是一种经典的调制方法，该方法通过对干涉仪的一路施加一个周期性的调制信号，使得干涉信号的相位避免保持在相位不灵敏位置，消除系统初相位及部分环境因素的影响。对于PGC 调制信号的典型解调方法有差分交叉相乘法（differential cross multiplication，PGC-DCM）和PGC 反正切法（PGC-Arctan）[13-14]。PGC-DCM 解调算法的结果与光源稳定度及调制深度相关，解调方法也较复杂。PGC-Arctan 解调算法在一定程度上可以消除光强扰动，其解调结果与调制深度有关。当调制深度C偏离2.63 rad 时，会出现严重的谐波干扰。可以说这些基于干涉的经典解调方案对于光纤激光水听器有一定程度的不适用。近年来，一些基于传统算法的改良算法被相继提出。朱俊等人引入DDS 从硬件上对PGC-DCM算法进行改良优化了载波信号的生成[15]。夏浩提出双微分交叉相乘算法（double differential cross multiplication，PGC-DDCM）、微分自相乘积分法（differential self-multiplication integration，PGC-DSMI）[16]，Ailing Z 等提出非对称相除差分自乘法（asymmetric division and a differential-self-multiplication PGC-ADDSM）[17]等，它们都能抵抗光强干扰，降低谐波失真，但解调过程较复杂，不利于实时监测。

本文基于DFB 光纤激光水听器提出了一种新的解调算法，它是基于双通道单路微分相除算法（single differential division，PGC-SDD）。相比于传统的解调方法，它更好地解决了光强扰动和调制深度变动的影响，同时针对DFB 光纤激光水听器中弱光信号条件有着更好的表现。此外，相比于其它的改进算法，该算法以较少的计算步骤完成信号的解调，有利于实现光纤激光水听器的实时性。

1 光纤水听器解调算法原理

基于传统解调算法的不足，本文提出基于双通道的单路微分相除算法。通过非平衡干涉仪获得的待解调信号I(t)[18]可以表示为

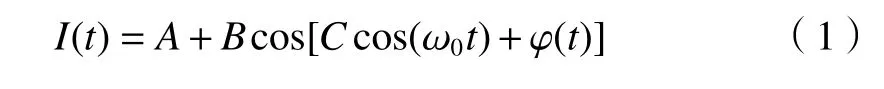
式中：A是与光源光功率的稳定度，干涉仪的输入光强，3 dB 耦合器等器件的插入损耗相关的直流项；B是干涉信号的幅度；C表示调制深度；φ(t)是待检测信号（包括外界环境噪声等）；Ccos(ω0t)是对非平衡干涉仪的一臂使用PZT 进行载波调制后产生的相位差；ω0为调制信号的角频率。

PGC-SSD 算法流程图如图2所示。I(t)为待测信号；Gcos(ω0t)和Hcos(2ω0t)为1 倍和2 倍载波信号；表示乘法器；LPF 表示低通滤波器；DIFF 表示微分器；表示除法器；表示积分器；BDF 表示带通滤波器。

图2 PGC-SDD 算法流程Fig.2 Flow diagram of PGC-SDD algorithm

将（1）式用Bessel 函数展开得：

将上式分别乘以1 倍载波信号Gcos(ω0t)和2 倍载波信号Hcos(2ω0t)，得到：

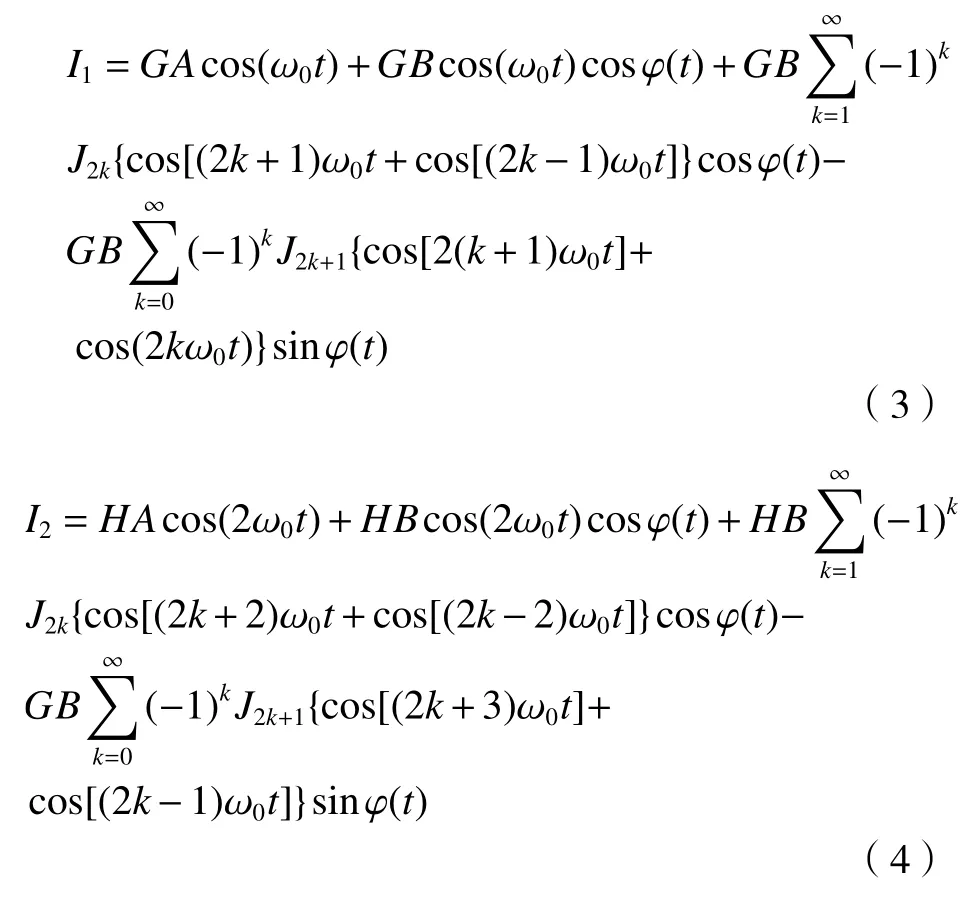
调制频率ω0远大于探测信号φ（t）中各频率项，故通过低通滤波器后ω0及其倍频项均被去除，可得输出信号L1和L2分别为

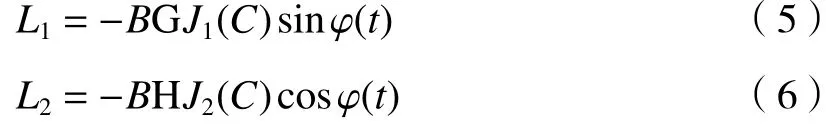
对（5）式进行微分处理，得L3：

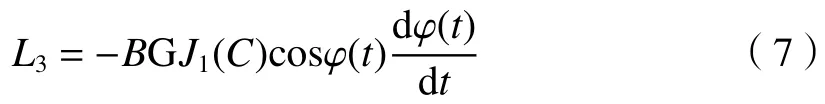
将（7）式除以（6）式可得L4：

将（8）式积分并令G=H，则解调结果为从计算结果可得，最终解调结果与干涉信号的强度无关，故由于外界或系统本身引起的干涉信号的强度变化不会影响解调结果。同时，解调结果仅与的比值成正相关，调制深度C 发生微小变化时不会使解调结果失真。

在传统的解调算法中，PGC-DCM 算法和PGCArctan 算法的流程图如图3和图4所示，其中 表示减法器，Arctan 表示进行反正切运算。

图3 PGC-DCM 算法流程Fig.3 Flow diagram of PGC-DCM algorithm

图4 PGC-Arctan 算法流程Fig.4 Flow diagram of PGC-Arctan algorithm

PGC-DCM 算法的解调结果[13]L5：

PGC-Arctan 算法的解调结果[13]L6：

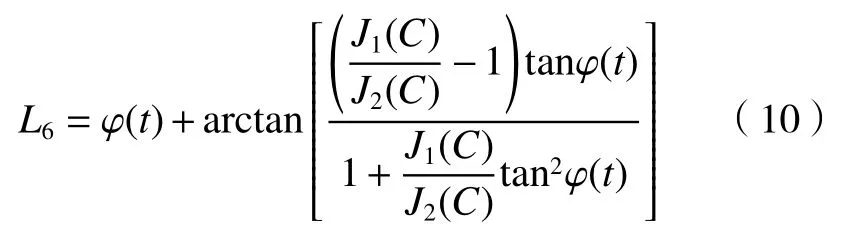
从（9）式可以看出解调信号幅度同时受到干涉光强与调制深度的影响。从（10）式可以看出，这种方法排除了干涉强度的影响。但调制深度变化时，相应发生变化，这种变化对于解调结果的影响是非线性的，会使解调结果产生失真，影响探测信号的还原。

2 仿真与实验

2.1 算法仿真

由前面分析可知，当调制深度C变化时，J1(C)J2(C)和也会发生相应改变，具体变化如图5和图6所示。

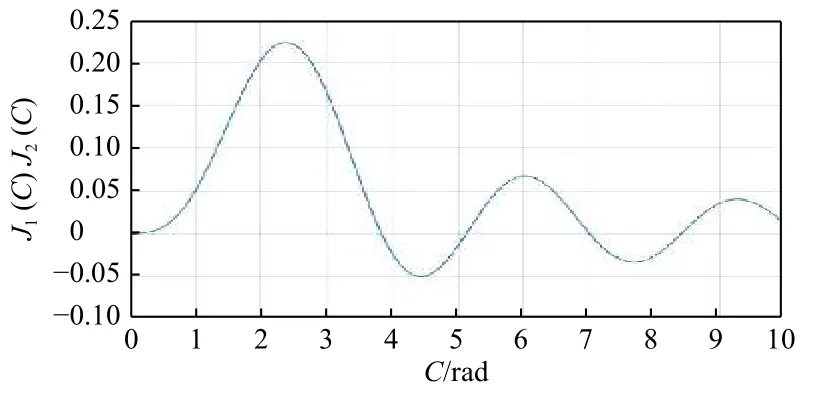
图5 J1（C）J2（C）随C变化的曲线图Fig.5 J1（C）J2（C）curve graph varying with C

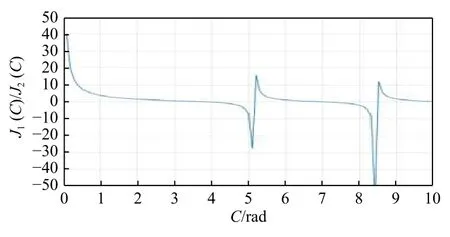
图6 J1（C）/J2（C）随C 变化的曲线图Fig.6 J1（C）/J2（C）curve graph varying with C

C值的大小由光波长及解调系统的光路结构决定，一般希望C值尽可能大从而增强PGC 方法的抗相位衰落作用。由上一部分的理论计算可得，J1(C)J2(C)和会对解调结果产生较大影响。结合图5及图6的变化曲线，为了减小系统工作时C值变化带来的影响，应在保证C值较大的情况下选取曲线变化平缓的区域。

在LabView 中建立仿真模型：待测信号为1 kHz的余弦信号；系统采样率为500 kHz；载波频率为10 kHz。分别对3 种算法进行仿真解调，得到仿真对数振幅谱如图7所示。

从图7（a）中可以看出，DCM 解调结果并不理想，这是受到干涉强度变化及调制深度变化共同作用的结果，对解调影响较大。在图7（a）及图7（b）中，均能明显观察到1 000 Hz 的高次谐波的频率峰值，说明解调结果受到了谐波的影响，存在相应的非线性失真。在图7（c）中，我们可以看到解调结果较稳定，频谱高次谐波不明显，说明该算法具有稳定性高、谐波失真小的优点，较好地抑制了光强及调制深度引起的光强畸变和谐波畸变。当外界的干扰引起了调制深度的飘移，其最终的解调结果也不会发生很大变化。

2.2 实验验证

根据图8搭建了基于马赫-曾德干涉原理的实验平台，采用λ/2 相移光栅（如图1所示，未加材料封装）。当980 nm 的泵浦光经过980 nm/1 550 nm波分复用器（wavelength division multiplexing，WDM）后，进入由相移光栅构成的光纤激光谐振腔中。其泵浦光会对铒离子进行抽运，激发中心波长为1 550 nm附近的单纵模相干光，此相干光一部分反射回WDM，经过马赫-曾德干涉仪后进入解调系统。其中，光隔离器是用来隔离马赫-曾德反射的光进入光纤激光器，避免对单纵模相干光造成影响；PZT 是对马赫-曾德干涉仪的一臂进行调制，产生相位延迟，最后和另一臂光在耦合器中相干耦合进入解调系统。

在解调系统中，设系统采样率为500 kHz，载波频率为10 kHz，待测信号频率为1 kHz，测得的频谱图如图9所示。

图7 3 种算法仿真解调对数振幅谱Fig.7 Log-amplitude spectrums of simulated demodulation with three algorithms

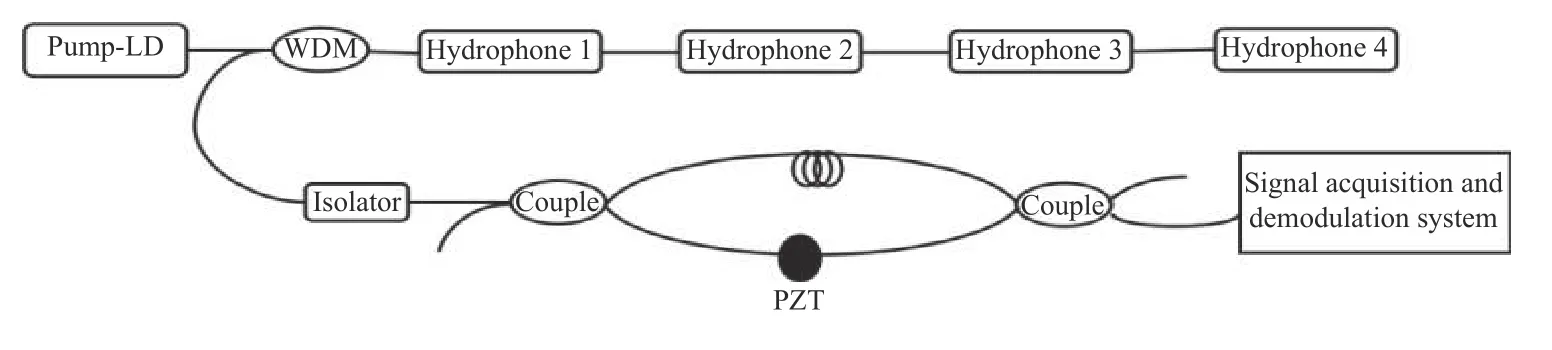
图8 基于马赫-曾德干涉原理的DFB 光纤激光水听器系统Fig.8 DFB optical fiber hydrophone system based on Mach-Zehnder interference principle

图9 3 种算法测试的线性振幅谱Fig.9 Linear amplitude spectrums tested by three algorithms

由图9的实验结果可以看出，3 种解调方案均能够检测出待测信号。由于受到干涉强度的影响，DCM 解调算法获得的频谱幅值很低，而反正切算法与改进算法幅值相近。观察后两者的频谱分布，反正切算法解调结果的频谱中主峰次峰比值约为2.5，改良算法约为4.3。结合其它临近频率的分布情况，可以看出改良算法解调信号的失真程度更小。最终通过计算，采用DCM 解调其信噪比约12.4 dB，Arctan 算法的信噪比约13.9 dB，SDD算法的信噪比达到了17.5 dB，新的改进算法解调信噪比较高，解调效果更好。

3 结论

光纤水听器由于其特有的体积小，抗电磁干扰等特点，在水下目标探测中得到了广泛应用。光纤激光水听器凭借良好的单色性和稳定性，能够大大提高探测灵敏度，从而获得了较快发展。在DFB 光纤激光水听器的应用中，相比于应用于干涉型水听器的经典解调算法，该解调算法在适应光纤激光水听器中微弱光信号的同时，在一定程度上消除了光强扰动和调制深度变化产生的影响。并在解调精度、信噪比等性能上具有优势。与已有的改进解调算法相比，该算法具有较少的运算步骤与较快的运算速度，有利于实现光纤水听器的实时解调。为了进一步优化算法解调能力，后期将会把封装好的基元进行组网放在湖中进行测试。检验该算法在复杂环境下的表现，并根据实验情况进一步优化和改进。