粒子群优化算法与灵敏度分析在电力系统无功优化中的研究

2020-06-04刘海锋卢屹磊戴喜明

河北电力技术 2020年2期

刘海锋，卢屹磊，戴喜明

(国网河北省电力有限公司检修分公司，石家庄 050071)

1 概述

电力系统无功优化问题属于混合的非线性规划的问题，其变量的连续与离散的混合，以及多约束项的问题使优化变得十分复杂。粒子群优化算法[1]是一种基于多点随机搜索的启发式智能算法。采用多点并行的搜索方式，易于实现，需要调整的参数少，适合工业生产应用。

灵敏度分析[2]是指以状态变量表示系统运行状态变化的敏感程度。对于无功[3]规划问题，就是配电网中节点无功的变化对系统有功网损的影响。选取灵敏度较高的节点作为无功补偿的切入点，从而减小配电网无功补偿计算时的搜索空间[4]。

2 数学模型建立

2.1 粒子群优化算法的数学模型

在连续空间中，粒子群优化算法可解释为:种群中第i个粒子可用xi表示，速度用vi表示，种群中2个最优解可表示为Pi和Gi，第i个个体粒子在空间中找到的最优解为Pi，整个种群在空间中找到的最优位置解为Gi。粒子根据粒子的当前位置xi，个体最优解以及全局最优解来更新自己的位置，按照以下公式进行迭代计算:

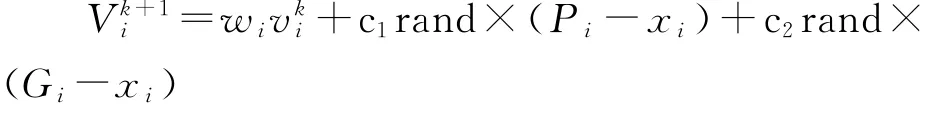
式中:w为惯性权重，其决定上一次迭代的速度对当前速度的影响程度，加速常数c1c2是2个非负值，一般c1=c2。rand是0到1之间的随机常数。

第一部分wivki表示粒子对先前速度的继承，其使粒子对搜索空间有扩张趋势，增强算法的全局搜索能力，第二部分c1r and×(Pi-xi)表示粒子根据自身经验所向往的飞行方向，第三部分为群体所向往的飞行方向。这样3个部分共同作用即能求得粒子的下一位置。

2.2 灵敏度分析的数学模型

结合灵敏度分析和粒子群优化算法确定进行无功补偿装置的优化配置。引入灵敏度分析，以确定无功补偿设备的候选节点[5]，然后再用粒子群算法进行优化计算确定补偿装置的位置和容量。

灵敏度表示状态变量对控制变量变化的敏感程度，对无功优化问题而言，就是系统网损对节点无功变化的灵敏系数。

节点无功变化对系统有功网损的灵敏度可表示为:

式中:Q、U、δ分别为配电网节点注入的无功节点电压幅值和相角。

对于系统第i个节点，则有

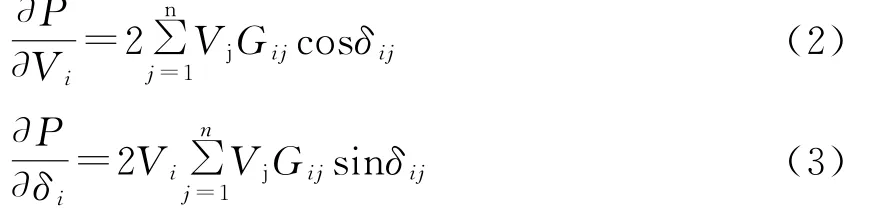
在求得各节点灵敏度系数以后，选取支路上灵敏度较高的2、3个节点作为进行无功补偿的候选位置。这样进行无功补偿时就能补偿于效率最高的节点。

2.3 无功优化的数学模型

电力系统无功优化是在给定的运行方式条件下，在满足各种约束项，通过对无功补偿装置的投切、调节压变压器分接头和发电机机端电压的配合等，实现目标函数的优化。

2.3.1 目标函数

以系统网损最小为目标函数:min f(x1，x2)

其中:f(x1，x2)即为系统有功网损，控制变量x1=[QTC，VTG，TTB]T，QC为无功补偿装置构成的向量，VG为发电机机端电压幅值构成的向量，TB为可调变压器变比构成的向量。

状态变量x2由全部节点电压幅值和发电机无功功率构成的向量。

2.3.2 约束条件

根据电网设备的实际情况设置约束条件，有等式约束和不等式约束两大类。功率平衡方程:

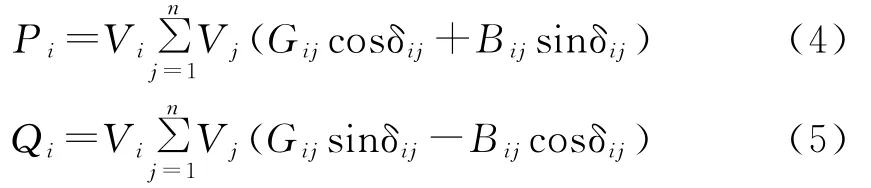
无功补偿装置容量的上下限:QCimin≤QCi≤QCimax;机端电压幅值的上下限:VGimin≤VGi≤VGimax;变压器变比的上下限:Ttimin≤Tti≤Ttimax;发电机无功出力上下限:QGimin≤QGi≤Qgimax;节点电压上下限:Vimin≤Vi≤Vimax。

3 应用粒子群优化算法求解无功优化的过程

应用粒子群优化算法求解无功优化问题时，将xi定义为粒子的位置，可行域的边界由Qc，VG，TB的边界来确定。运用粒子群优化算法求解无功优化的过程如下。

a.输入系统数据，初始化粒子群。首先输入系统结构，网络数据和控制参数。由发电机节点电压的上下限，然后确定粒子的维数，即一组控制变量的变量数，在可行域中随机产生N个粒子，作为初始粒子群。同时随机初始化粒子的飞行速度。此时，迭代次数记为0。

b.计算目标函数值。对群体中每个粒子，分别进行潮流计算，计算出每组控制变量的有功网损。并判断是否违反节点电压和发电机无功出力的约束，将惩罚函数计入到目标函数中。

c.记录2个极值，个体极值和群体极值。比较所有粒子对应的目标函数值，首先记录粒子i(i=1，2，…，N)当前的个体极值Pbest及对应的目标函数值F(Pbest(i));从Pbest(i)中确定整体极值Gbest，并记录Gbest对应的目标函数值F(Gbest)。

d.更新k=k+l。更新各粒子的飞行速度。这样，对于粒子i就得到一个确定的趋向的Pbest和Gbest飞行速度vi。然后更新粒子的新位置。

e.重新计算各个粒子此时的目标函数值，判断是否更新Pbest和Gbest:对于粒子i，比较第k+l次迭代中得到的函数值F(i，k+l)与F(Pbest(i))，若F(i，k+l)＜F(Pbest)，则F(Pbest(i))=F(i，k+1)(i=1，2，…，N)，并更新，否则不更新。更新全部粒子极值后，取最小的Pbest，判断是否需要更新Gbest。

f.判断是否收敛，当全局最好位置大约20次无变化，或者达到最大迭代次数时，停止迭代。

对于惯性权重w和最大迭代次数itermax，w不仅控制本次飞行速度对下次飞行速度的影响程度，还体现着粒子群优化算法对全局搜索与局部搜索的平衡。在搜索的前期，权重系数大，可以提高全局搜索能力;随着搜索逾趋于全局最优解逐渐减小，则加强了局部搜索能力并加快了收敛速度。本文假定w呈线性下降，计算方式如下:

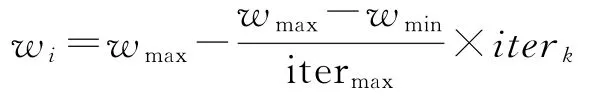
为了取得较好的结果，需要设置最大飞行速度，则粒子的飞行速度的取值范围为[-vmax，vmax]，如果vmax过大则会导致搜索过粗略，错过最优解，如果vmax过小则会导致搜索不了全区域，找不到最优解。

4 典型系统的无功优化结果分析

文中采用粒子群优化算法对电力系统标准节点系统IEEE-14进行优化计算。

4.1 初始潮流计算

该系统包含5台发电机(节点1、2、3、6、8，其中节点1为平衡节点，其余为PV节点)，3台可调变压器(支路4-7，4-9，5-6)。文中将节点2和3的发电机、支路4-7和5-6的变压器设为优化对象，静止无功补偿点由灵敏度计算结果决定。系统初始有功功率损耗为15.218 2 MW。

IEEE-14节点系统的初始潮流数据各个节点的电压水平在1.0～1.1，节点电压水平较高且没有出现越限;节点1的发电机无功处理越下限。因此对IEEE-14系统的无功优化目的是降低系统网损同时使节点1无功出力不越限。

控制变量分为发电机节点电压、变压器变比以及无功补偿点的无功补偿容量，其约束条件可设置为:可调发电机电压上下限设置为1.0±0.1，可调变压器变比上下限设置为1.0±0.1，调节步长为0.025，变压器档位设置为-4～4，无功补偿点补偿容量约束为0≤QC i≤0.5。

4.2 灵敏度分析结果

由灵敏度公式可知，网损对无功的灵敏度为正时，增大无功可减小网损，反之，网损对无功的灵敏度为负时，减小无功可减小网损。

根据潮流计算的初始结果可得到节点导纳矩阵、各节点电压的幅值和相角，以此可求出各节点的灵敏度。节点12灵敏度为0.460 1，节点13灵敏度为0.455 1，其他节点均在0.455以下，故节点12、13选为无功补偿点，与其他控制变量一同优化，且灵敏度值均为正，说明增大补偿点的无功注入能够降低网损值。未出现的节点为平衡节点或PV节点，不能选为无功补偿点，因为这些节点的无功功率在潮流计算中不是作为已知量出现，不能影响计算结果。

4.3 优化结果对比

粒子群优化算法的参数设置为:加速因子c1=c2=2，惯性权重ω随迭代次数从0.9线性减少到0.4，种群数为300，迭代次数50次。2个算例各运行30次，取结果平均值。优化结果见表1。

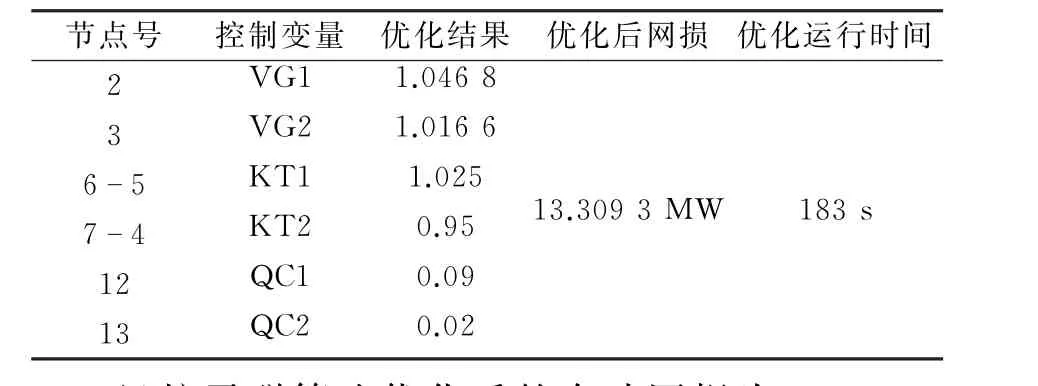
表1 IEEE-14节点无功优化结果

经粒子群算法优化后的有功网损为13.309 3 MW，网损下降率为12.81%，优化运行时间为183 s。其中2节点和3节点发电机电压分别上升0.046 8和0.016 6;支路6-5的变压器上调1档，支路7-4的变压器下调1档;12节点和13节点电容器分别投入9组和2组。算法的收敛情况如图1所示，在第41次达到收敛。

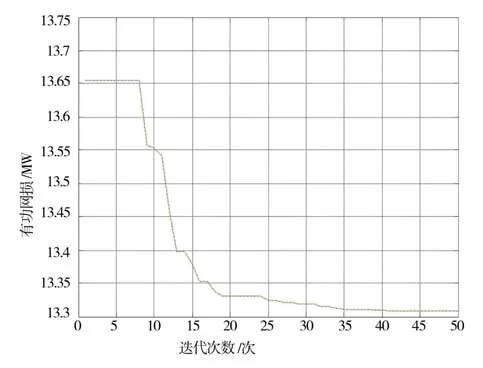
图1 IEEE-14迭代收敛曲线

通过对控制变量的适当控制可有效降低网损，改善节点电压而提高电网的安全性。灵敏度分析与粒子群优化相结合的算法进行了无功优化问题的求解。在求解过程中，首先通过对节点灵敏度的计算，找出无功补偿候选位置，进而缩短用粒子群算法的搜索时间，优化的结果在要求的范围内。通过对IEEE-14节点的算例分析表明，灵敏度分析和粒子群优化相结合的算法比基本的粒子算法结合，节省了粒子的搜索时间，同样可以获得全局最优解，在大多数情况下，可以收敛至满意解。与其他人工智能算法相比较，其优势在于没有较多的参数需要调整，更加简单，容易实现且收敛速度快，可有效用于求解无功优化问题。