基于HYDRUS-MODFLOW的大洋河岫岩流域地表水与地下水耦合模型
2020-06-04张贺
张 贺
(辽宁润中供水有限责任公司,辽宁 沈阳 110166)
1 研究区概况
大洋河发源于岫岩县偏岭乡境内的一棵树岭南侧,流经岫岩县、东港市,在东沟县的黄土坎入黄海[1],干流全长230 km,主要支流有雅河、牤牛河、连河、哨子河等,全部流域面积6004 km2,多年平均径流量31 亿m3。其中,大洋河岫岩县境内长度180.2 km,流域面积1968.4 km2,是岫岩县的重要饮用水水源地[2]。大洋河岫岩流域位于辽东半岛东部,地貌以低山丘陵为主,呈现出西北高,东南低的特点。研究区属于温带湿润性季风气候,多年平均气温为8 ℃,多年平均降水量为767 mm,多年平均蒸发量为1066 mm。由于研究处于距离黄海较近的东部迎风坡,因此受季风影响比较显著,汛期的7 月、8 月集中了全年6 成以上的降水[3]。研究区的地下水主要是松散岩类孔隙水,且主要富集于全新统地层中,沿河谷和山间谷地均有分布,成因主要是冲积、冲洪积、坡洪积等。根据地质钻孔和民井调查资料,含水层分布在阶地和河漫滩中,上覆黄褐色亚砂土层厚度为1.0 m~1.5 m,粗砂和砂砾石互层厚度为2 m~3 m,底部的砂砾卵石层厚3 m~5 m,含水层总厚度为4.5 m~6.5 m。研究区的地下水主要是侧向径流补给、大气降水补给、农田灌溉水渗入补给以及开采条件下的河流入渗补给。随着经济社会的发展,研究区的水资源需求量逐年攀升,而气候变迁的大背景下,研究区的水资源总量呈递减状态。因此,地下水资源的不断开发利用将成为研究区的必然趋势。所以,加强地下水资源研究,对研究区水资源的合理开发和利用具有重要意义。
2 耦合模型的构建
2.1 构建思路
流域内的水循环是一个十分复杂的运动过程,而地表水和地下水两种主要水资源形式的赋存和运动状态之间也存在显著差异[4]。基于水循环的复杂性以及地表水和地下水循环上的差异,当前的流域水循环的研究主要为地表水或地下水的单独模拟。然而,上述研究模式中水循环过程缺失是不可避免的,研究成果的精度也难以贴合实际。因此,要获得较高精度的模拟成果,需要将地表水与地下水这两种主要水资源形式进行综合研究[5]。本文研究利用地下水模型MODFLOW模型,结合研究区地表水文资料进行参数率定,在校验准确并满足模型精度要求的基础上(限于篇幅这里不再详述),将其输出项作为Visual MODFLOW的输入项对研究区地下水进行数值模拟,试图通过地表水和地下水的耦合模拟,提高模拟精度[6]。
2.2 模型准备
大洋河岫岩流域的孔隙水在天然状态下的水力坡度不大,渗流状态也基本符合达西定律。因此,地下水的水流形式可以概化为平面二维流,同时在计算时段内表现为非稳定流特征。研究区的地下含水层可以概化为非均质各向同性的潜水层,且下部直接与不透水黏土层相接。基于此,研究区的南北方向边界设定为零流量边界条件,东西方向为GHB通用水头边界[7]。模型的计算时间为2006 年1 月~2015 年12 月,地下水模型MODFLOW的计算步长和应力期均设定为1 d,全部计算时段共3650 个应力期。非饱和带模型HYDRUS的初始时间步长设定为0.5 d,最大和最小时间步长分别为1 d和0.3 d。研究区地下水的初始水位采用2006 年1 月1 日的观测井实测数据。
2.3 网格剖分
在HYDRUS-MODFLOW地表水和地下水耦合模型时,首先利用MODFLOW模型对大洋河岫岩流域进行空间离散。网格单元在X方向和Y方向上的尺寸分别为974.55 m和913.05 m,最终划分为2678 个计算单元。在竖直方向上,根据观测井的实测地下水位数据,确定出含水层的饱和带与非饱和带的厚度。然后,利用HYDRUS模型,在研究区的水平方向上,根据下垫面以及土壤特性,研究区划分为150 个土壤单元体,每个土壤单元按照不同深度部位的特征划分为3 个~38 个计算节点,进而实现土壤单元体的有限元网格划分[8]。
2.4 模型输入
由于MODFLOW是具有模块化结构的模型,而基于HYDRUS-MODFLOW地表水和地下水耦合模型的基本思路是将HYDRUS子程序嵌入到MODFLOW主程序中[9]。因此,在耦合模型中选择最适合的模块进行模拟。结合本次研究的实际情况,增加河流子程序以及地表产汇流过程,以实现对研究区的地表水文过程的模拟。
2.5 参数的率定
根据研究区土壤的实际情况,对土壤类型进行概化分为亚砂土和亚粘土两个类型,其水力参数的初始值根据相关研究成果确定,然后利用人工试错法对参数进行反复调整,直至模型的模拟和实测结果之间具有良好的拟合度,率定后的模型参数见表1。

表1 参数率定结果
3 计算结果与分析
3.1 地下水位拟合结果分析
由于设置的模型模拟应力期长度为1 d,共3650 个应力期,数据量较大,因此在统计数据过程中选择以月为时间单位,共120 个月。利用模型的模拟结果和观测井的实测值,对研究区所有的125 眼观测井的地下水位的平均值进行对比,获得图1 和图2 所示的模拟和实测地下水位过程和线性相关图。由图1 可知,研究区的地下水位的模型模拟结果和实测值具有基本一致的走向变化,具有较好的拟合度。由图2 可知,研究区地下水位的模拟值与实测值的水位散点基本都落在直线附近,说明两者之间的相关性较好,计算两者之间的相关系数,结果为0.79。由此可见,整个流域的实测值与模型的模拟值之间具有较好的吻合度。

图1 地下水位模拟值与实测值关系图

图2 模拟和实测地下水位散点图
鉴于研究区内地表水和地下水的补排关系十分密切,是研究区地下水位的重要影响因素,因此距离河道较近区域的地下水位受河流径流影响比较显著,变化也比较剧烈。因此,研究中选择位于河道附近的岭沟46#、39#、12#、23#、17#观测井,哨子6#、14#、17#、24#、31#观测井等10个代表性观测井进行地下水位模拟,并与实测值进行对比。其中,岭沟46#、39#观测井和哨子6#、14#观测井的地下水位过程模拟和实测结果见图3 ~图6 。由模拟结果可知,大部分观测井的模拟结果和实测结果之间具有良好的拟合度,仅有个别监测井部分时段的模拟误差较大。究其原因,主要是部分地区的土壤类型和下垫面变化过于复杂,地下水的开采量难以进行准确估算,同时枯水年份地下水位受到灌溉用水的影响比较大等。
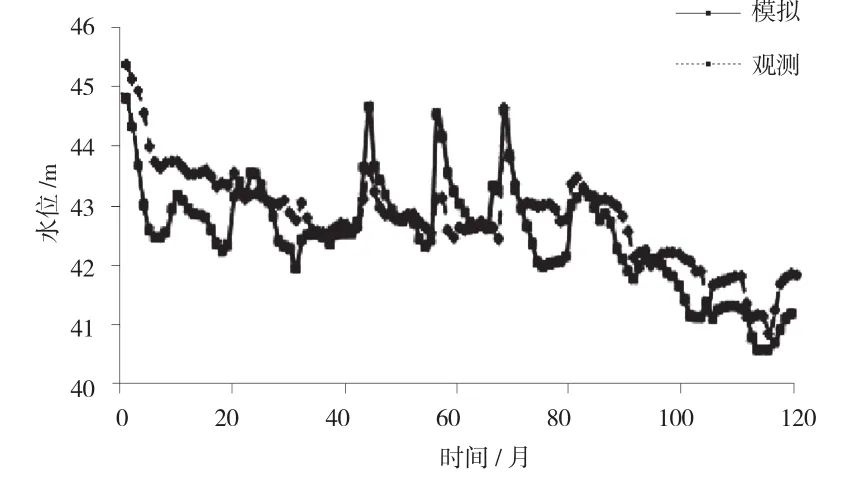
图3 岭沟46#观测井模拟和实测地下水位过程
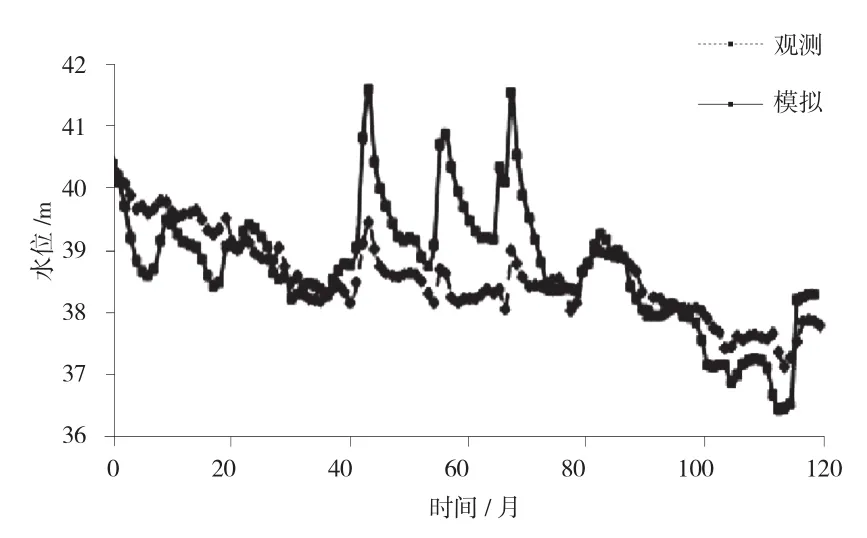
图4 岭沟39#观测井模拟和实测地下水位过程
对上述10 个观测井的纳什效率系数和模拟的相对误差进行统计,结果见表2。由表中的结果可知。各个典型观测井的纳什效率系数的值均在0 附近波动,且波动幅度不大,说明各个观测井的模拟结果和实测结果比较接近。从相对误差的统计计算结果来看,各观测井的相对误差值在3%以内,也说明模型的模拟程度较好,可以用于研究区的地下水流动过程的模拟计算。

表2 各观测井的误差情况分析结果
3.2 出口断面流量过程计算结果分析
为了进一步验证模型的模拟能力,对研究区出口断面的流量进行模拟计算,以便对模型的模拟效果进行验证。图7为根据模拟值和实测值绘制的逐日流量过程图,由图7 可知,模拟值和实测值之间具有良好的拟合度。具体来看,在参数的率定期和验证期,纳什效率系数分别为0.81 和0.79,径流量相对误差分别为3.66%和3.85%,整个模拟期的纳什效率系数为0.79,径流量相对误差为0.44%,各个阶段和整个模拟期的纳什效率系数和径流量相对误差均在允许范围内。
鉴于模拟期间的1999 年、2000 年以及2001 年,由于降水量偏大造成径流量变幅较大。因此对选取其中变幅最大的2000 年,进行逐日流量的模拟值和实测值对比,结果见图8。由图8 可知,模型的模拟值和实测值之间具有良好的拟合度,纳什效率系数为0.88,相对误差为6.23%,均在允许范围内,说明模型在出口断面流量变幅较大的情况下,亦可以获得良好的模拟效果。
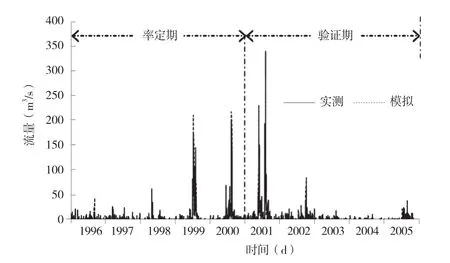
图7 模拟与实测逐日流量过程
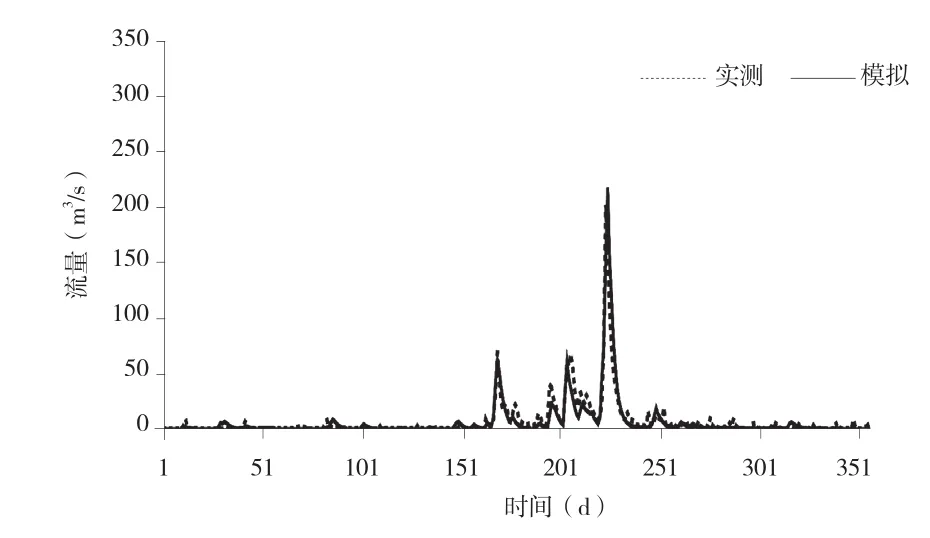
图8 2000年模拟与实测逐日流量过程
4 结论
以辽宁省大洋河岫岩流域为例,对基于HYDRUSMODFLOW的地表水和地下水耦合模型进行研究,获得如下结论:
(1)研究区的地下水位的模型模拟结果和实测值具有基本一致的走向变化,两者之间的相关系数为0.79,具有较好的拟合度。
(2)研究中选择位于河道附近的10 个代表性观测井进行地下水位模拟,并与实测值进行对比。由模拟结果可知,各个典型观测井的纳什效率系数值均在0 附近波动,相对误差值在3%以内,因此模拟结果和实测结果之间具有良好的拟合度。
(3)对研究区出口断面的流量进行模拟计算,结果显示整个模拟期的纳什效率系数为0.79,径流量相对误差为0.44%;对径流量变幅较大的2001 年的逐日流量的模拟值和实测值进行对比,结果显示模拟值和实测值之间具有良好的拟合度,纳什效率系数为0.88,相对误差为6.23%,均在允许范围内。
(4)综合上述,基于HYDRUS-MODFLOW的地表水和地下水耦合模型具有较高的模拟精度和适应性,可以用于研究区的相关研究。
