静息态功能磁共振成像评估健康老年人认知行为的多尺度熵模型研究*
2020-06-04张夫一葛曼玲郭志彤谢冲杨泽坤宋子博
张夫一 葛曼玲† 郭志彤 谢冲 杨泽坤 宋子博
1) (河北工业大学, 省部共建电工装备可靠性与智能化国家重点实验室, 天津 300130)2) (河北工业大学, 河北省电磁场与电器可靠性重点实验室, 天津 300130)(2020年1月8日收到; 2020年3月20日收到修改稿)
当前, 静息态功能磁共振成像(rfMRI)为脑功能检测提供了高效、快捷的先进技术. 熵可以捕捉神经信号动态特征, 可作为量化评估参数, 但尚存在固定尺度计算缺陷且对认知行为的生物学标记少有研究, 影响检测精准性. 为此, 本文将多尺度熵模型与机器学习方法联合, 寻求BOLD 信号复杂度表征健康老年人认知分数的功能影像学标记. 由扫描前认知量表测试分数将98 名健康老年人分为优、差两组, 78 名纳入训练,20 名纳入测试. 首先, 构建多尺度熵模型, 计算两组扫描数据熵, 统计和对比以优化模型参数; 然后, 在优化参数下由统计显著性高的脑区熵值构建特征向量; 最后, 用极限学习机对两组分类并统计检验. 发现:rfMRI 多尺度熵在评估老年人认知分数时, 在额、颞叶脑区存在较大显著性差异, 以此为标记区分认知分数可达80%准确率. 结论: 额、颞叶等脑区优化的多尺度熵可有效区分健康老年人认知行为优劣. 该研究将为rfMRI 替代主观繁琐的传统认知量表测试提供新的检测参数和新方法.
1 引 言
随着全球人口老龄化形势日益严峻, 老年人群体健康状况越来越受到关注, 尤其是认知水平关乎生命质量而受到格外注意, 尽早了解老年人认知能力状况, 是采取预防或干预措施以减缓退行性或病理性认知功能减退的重要前提, 特别是对具有日常生活能力, 且精神、躯体和社会层面皆健康的老年人(健康老年人)认知能力的检测, 是区分退行性和病理性减退的基础, 也是评估认知障碍的先决条件, 因而显得尤为重要.
大脑是复杂的非线性系统, 从非线性动力学角度研究生理信号复杂度是脑科学的重要基础. 生理复杂度通常是通过量化分析检测信号时间序列的规律性(有序性)来评估生理活动的动态变化[1,2],可反映大脑在某些动态机制中功能状态的改变, 对其进行研究可提取大脑的健康(或疾病)状况以及脑状态变化特征, 从而实现精准有效的功能检测.
熵作为一个经典物理量, 被广泛应用于非线性序列分析中, 如医学、电力、机械等各个领域[3,4].熵模型经历了近似熵、样本熵、多尺度熵(multiscale entropy, MSE)等发展历史. 近似熵模型由Pincus[5]首次提出, 可从较少数据量中识别时间序列变化复杂度, 其优势之一是将复杂系统分类为确定性和随机性两类. 其后, 样本熵模型由Richman 和Moorman[6]将其改进和发展, 它可在计算概率时不包括自匹配, 消除了自匹配所产生的计算偏差, 因此, 它比近似熵更简单, 而且对时间序列长度依赖性更小, 被广泛应用于生理信号的时间序列计算中, 但固定尺度计算熵值很难捕捉病理变化. 为此, Costa 等[1,7]提出了MSE 概念, 用以表征生理系统在不同状态下所表现的复杂特性, 避免了从单一尺度上计算时间序列而导致的误差. 并且, 通过心率变异性研究发现: MSE 比单一尺度样本熵能更好地阐明在健康和疾病状态下人体生理信号复杂度的差别, 研究结果支持衰老和疾病的“复杂性损失”理论, 即随着人体衰老或疾病, 生理信号复杂度会逐渐减小.
在脑科学方面, 熵模型运用在脑电/脑磁[8,9]、功能磁共振成像[10]等信号处理上, 可从复杂度角度揭示大脑生理、病理和功能的变化规律. 大脑神经细胞在静息态(闭眼、清醒、无特定认知任务)下也存在协同活动, 并保持着在任务态时才出现的复杂网络系统, 低频波动的BOLD 信号并不是随机噪声, 而是反映了人脑自发神经活动, 具有一定生理意义[11]. 因无需受试者执行特定任务, 却可以用来研究人脑内在功能架构, 静息态下相关性和复杂度等检测算法受到当今科学研究和临床检测的青睐. 除了高空间分辨率和无损优势外, 静息态下功能磁共振成像(rfMRI)还比脑电/脑磁、任务态下功能磁共振成像等先进检测技术更简捷、快速(15 min 内), 比一贯使用的量表认知检测更客观、方便、快捷和高效, 因此, 这项技术成为替代传统检测手段的首选[11−14]. 另外, 从非线性系统角度出发进行BOLD 信号分析, 有助于深入认识复杂度这一评估参数的物理意义, 有利于提高检测精准性.
本文试图将多重物理量优化和现代机器学习方法相结合, 探讨rfMRI 信号复杂度区分认知分数的可能性, 为评估健康老年人认知行为(本文采用扫描前认知量表测试分数定义认知行为优劣)的先进技术提供新的参数和新方法. 首先, 基于rfMRI 信号优化多尺度熵模型的计算参数, 以寻求区分健康老年人认知行为优劣的脑功能影像学标记. 然后, 根据标记, 采用现代机器学习技术—极限学习机(extreme learning machine, ELM)对认知分数进行分类, 以实现客观、有效地评估健康老年人认知行为的研究目的, 加强rfMRI 技术在认知功能评估上的竞争力, 取代主观、繁琐的传统测试量表方法.
根据rfMRI 扫描前认知量表测试得分, 将98 位健康老年人分成认知分数优、差两组, 共78 人纳入训练集, 其余20 人纳入测试集, 在rfMRI预处理基础上, 本文采用了以下研究思路: 1)构建多尺度熵模型并优化算法参数; 2)在优化参数下统计显著性高的脑区熵值构建特征向量输入ELM; 3)利用ELM 对认知分数优、差两组进行分类, 并采用N 折交叉验证测试分类准确率; 4)总结并讨论MSE 模型在健康老年人rfMRI 检测和分类认知行为的研究结果.
本文强调了MSE 模型参数优化在探讨健康老年人脑BOLD 信号熵值区分认知分数优差中的重要作用, 为rfMRI 检测脑功能提供了新的评估参数和新方法.
2 材料与方法
2.1 被试与样本
本实验参与者样本取自公开数据集(github.com/juanitacabral/LEiDA), 以认知量表测试分数来区分认知行为优劣. 该数据集是从一项队列研究中挑选出来的, 涉及1051 位年龄在50 岁以上的葡萄牙老人, 他们曾进行过9 项神经心理学测试, 应用主成分分析(PCA)确定与记忆和认知执行功能相关两个主要维度得分, 再由聚类方法将得分由优到差排序为C1>C2>C3>C4 四 级, 其中C1和C4 对应最优和最差认知分数或优、劣认知状况.分别从上述C1和C4 档案中随机选择受试者扫描rfMRI 并签署知情同意书, 最终样本共含有98 名受试者, 其中55 名认知能力优秀的受试者(在此命名为认知分数优组)和43 名认知能力最差的受试者(在此命名为认知分数差组)[15−18].
2.2 数据获取
在接受扫描时, 参与者被要求保持静止、安静、闭眼且清醒的静息态. 功能磁共振成像在葡萄牙布拉加医院采集, 使用临床认可的1.5 T Siemens MagnetomAvanto 12 通道仅有头部线圈扫描仪. 采用BOLD 敏感回波平面成像序列, 参数如下: 30个轴向切片, TR/TE = 2000/30 ms, FA =90°, 切片厚度为3.5 mm, 切片间隙为0.48 mm,体素大小为3.5 mm × 3.5 mm, FoV = 1344 mm,180个数据.
2.3 数据预处理
rfMRI 数据预处理是使用FMRIB 软件库工具进行的[19−21]. 首先, 1)移除采集的前5个数据,以便信号稳定; 2)切片计时校正; 3)通过使用MCFLIRT[22]将每个体积的刚体对准采集的平均图像进行运动校正; 4)使用脑提取工具(BET)进行颅骨剥离[23]; 5)使用FLIRT 通过连续的刚体配准实现非线性归一化功能获取到结构获取, 非线性配准从结构原生空间到MNI 标准空间, 并使用FNIRT 重新采样到2 mm 各向同性体素大小[24];6)运动参数、平均CSF 和WM 信号的线性回归;7)回归残差的带通时间滤波(0.01—0.08 Hz). 然后, 在解剖自动标记AAL 图谱的90个大脑分区,平均每个脑区的所有体素上BOLD 信号形成用于多尺度熵计算和分析的时间序列.
2.4 样本熵
MSE 即多尺度样本熵, 它对生物医学信号具有较好的识别能力, 在计算概率时不包括自匹配,熵值较大表明所计算的时间序列具有较高复杂度,反之亦然.
对于长度为N的一维离散时间序列{x1,x2, ···,xN}, 在多个尺度下变换, 得到新的粗粒化时间序列
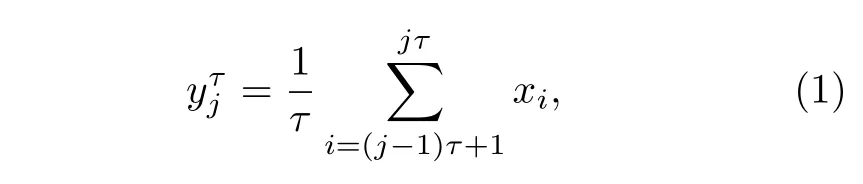
其中1 ≤j≤N/t,t为尺度因子的长度为L=N/t. 再构造一组m维向量(m即嵌入维数)Ym(i):Ym(i)=yi+k,0km −1 . 对每个i值, 计算它与其他值j的距离, 即Ym(i)和Ym(j)之间的距离:
设定公差阈值(即相似系数)r(r> 0), 再对每个i值计算的数目Bm(i) , 并计算与距离总数的比值:


相似地, 当维数为m+ 1时, 可得:
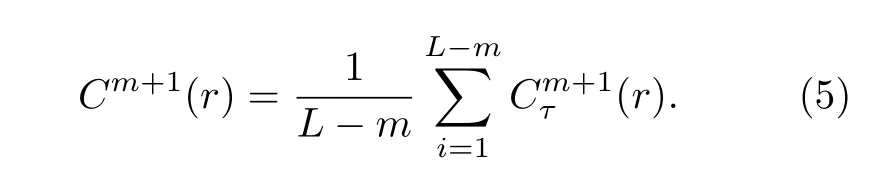
当L为有限值时, 可得出序列长度为L的样本熵估计值, 记为SampEn:

综上所述, 样本熵与嵌入维数m和相似系数r的取值有关.
2.5 MSE
以尺度为变量重复样本熵计算过程, 得到样本熵值在多个尺度取值下集合, 即MSE:
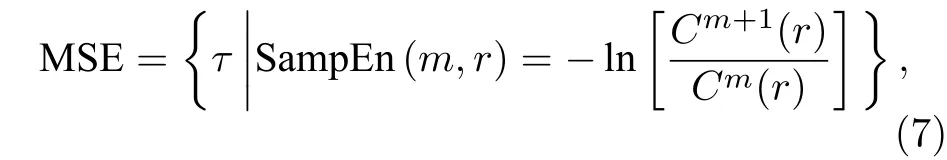
其中, 主要有3个参数决定MSE: 尺度因子t、嵌入维数m和相似系数r. MSE 可以通过在不同尺度下熵值变化研究系统复杂度的动态特性. 在相同参数取值下, 熵值较大表明所计算的时间序列具有较高复杂度, 反之亦然.
MSE 是通过不断调节尺度因子大小得到的样本熵集合, 故MSE 模型会随着信号复杂度不同而参数取值相异: 如, 用在脑电信号复杂度分析时,通常采用m= 2,r= 0.5[25];m= 2,r= 0.15[26];m= 1,r= 0.25[27]等; 再如, 用在fMRI 信号复杂度分析时, 通常选取m= 2,r= 0.3[10];m= 2,r= 0.46[28];m= 1,r= 0.35[29];m= 2,r=0.6[30]等. 很显然, 使用MSE 对生物医学信号进行处理时, 并不具有统一的参数取值标准或规范. 因此, 本文提出借助机器学习对认知分数优差两组分类效果进行评估来辅助优化熵模型计算参数的研究方案, 以使参数选择具有客观性, 并选择在优化参数上有一致性优良分类效果的脑区为区分认知分数的标志性脑区.
在优化MSE模型计算参数时, 有两点需要同时考虑. 第一点, 采用ROC(receiver operating characteristic)曲线联合AUC(area under curve)值反映认知分数优、差两组样本间显著性差异.ROC 曲线可直观显示分类效果, 而ROC 曲线下面积大小, 即AUC 值, 可用来量化评估分类能力高低, 取值范围一般在0.5—1 之间. 在本文中,AUC 可用数值给出熵模型参数优化的效果, 其值越大, 则优化效果越好, 反之亦然. 当AUC 取值分别 在0.9—1, 0.8—0.89, 0.7—0.79, 0.6—0.69,0.5—0.59 之间时, 则分别表示分类效果为极好、良好、恰当、较差、很差等5个档次精度. 本文使用SPSS 软件(IBM SPSS Statistics 21; USA)进行组间熵值数据差异显著性统计. 第二点, 考虑MSE 模型参数相互影响的特点, 本文采取在优化的每个步骤中3个参数全部参与评估优化效果的研究方案. 即当优化嵌入维数m和相似系数r时,采用了在3个参数皆参与分析优化效果的条件下,先获得优化空间再逐步获得优化值; 进一步优化尺度因子t时, 也是统筹3个参数参与下的分类效果来确定t的优化值.
在确定对认知分数敏感脑区时, 本文采用了ROC 曲线和AUC 值联合参与组间对比的方法,即: 通过组间对比, 观察熵模型参数对ROC 曲线影响来初步直观熵模型参数优化效果, 再联合AUC 值来量化评估标志性脑区. 当ROC 曲线总体呈现于参考线以上区域, 并远离参考线且AUC 较大时, 则认为总体上分类效果较佳, 可视作该脑区对认知分数较敏感, 该脑区可视为认知行为评估的标志性脑区; 反之, 则视作分类效果较差,该脑区不能作为标志性脑区.
2.6 特征向量
在经过优化的参数设定条件下, 将AAL 图谱中共90个大脑区域进行熵值计算并通过t检验(t-test)对认知分数在优与差组间进行差异显著性统计, 得出在每个大脑区域下, 认知分数优与差两组样本差异显著性统计值(p值), 并按照由小到大顺序排列, 优先选取p值较小且分类效果较好的脑区, 同时结合ROC 曲线和AUC 值来辅助选取标志性脑区. 在这些脑区上, 对经过优化参数模型计算所得熵值取平均值, 得到每个被试在对应脑区的平均样本熵值, 将认知分数优的样本类别标记为“1”, 将认知分数差的样本类别标记为“0”, 由此组成一个向量, 并与平均样本熵值组成特征向量, 作为两组被试认知分数的分类依据.
2.7 ELM 及N 折交叉验证
ELM 是现代机器学习模型, 相对于传统的人工神经网络模型, 其优势在于可随机产生输入层与隐含层间连接权值及隐含层神经元阈值, 且在训练过程中无需调整, 只需要设置隐含层神经元个数,便可获得唯一最优解. 为实现优、差两组的准确分类, 需要进行ELM 创建、训练和仿真测试, 图1为ELM 分类模型的具体流程图.
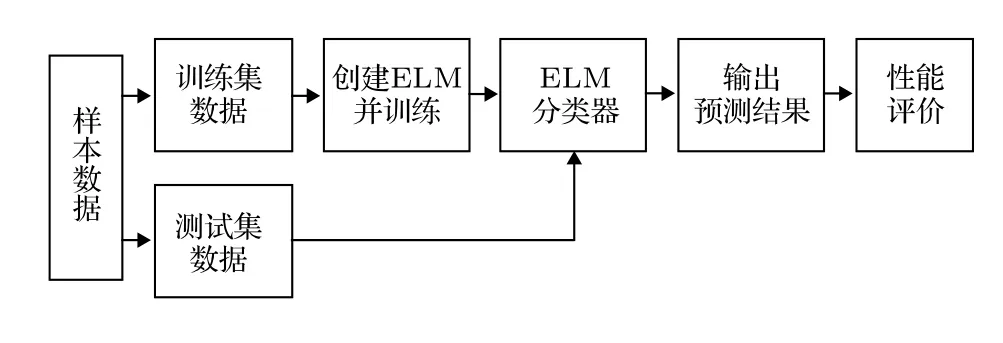
图1 ELM 分类器操作流程图Fig. 1. Flowchart of ELM classifier.
ELM 模型主要步骤描述如下:
1)为了使得建立的模型泛化性能良好,ELM 要求具有足够多的训练样本且具有较好的代表性. 同时, 训练集和测试集格式应符合ELM 训练和预测函数的要求;
2) 通过elmtrain( )函数创建、训练ELM, 由于隐含层神经元个数对ELM 性能影响较大, 故需要不断试凑以选择适量的隐含神经元;
3) 通过elmpredict( )函数进行ELM 仿真测试, 获得测试集;
4) 通过测试集分类结果, 可以对模型的分类准确率进行评价.
本文在认知分数为差组的43 名被试中, 随机抽取33 名熵值数据作为训练集, 余下10 名数据作为测试集; 在认知分数为优组的55 名被试中, 随机抽取45 名熵值数据作为训练集, 余下10 名数据作为测试集. 即, 共78 名被试组成训练集, 20 名组成测试集. 然后, 创建ELM, 将类型参数TYPE 设为1(1 表示解决分类问题, 0 表示解决回归问题);并设置隐含层神经元个数N= 500; 将激活函数TF 设置为“sig”类型, 在ELM 中对数据进行训练和仿真. 最后, 通过结果对比, 得出测试集数据的分类准确率.
在ELM 等机器学习模型中, 常用N折交叉验证(N-fold Cross Validation)来测试算法准确性:在样本量较少的情况下, 为了充分利用数据集对算法效果进行测试, 将数据集分成N份, 轮流将其中N-1 份作为训练数据, 1 份作为测试数据, 进行试验, 每次试验都会得出相应的正确率(或差错率).N次结果的正确率(或差错率)平均值用来估计算法精度. 交叉检验优势在于, 保证每个子样本参与训练且都被测试, 降低泛化误差, 常用的有5 折交叉验证、10 折交叉验证(即N分别取5, 10)等. 本文使用了10 折交叉验证获得分类精度.
3 结 果
3.1 MSE 模型的计算参数优化
本文通过组间对比获得显著性差异以及ROC 曲线和AUC 值评估, 共获得3个MSE 模型的优化参数值.
3.1.1 嵌入维数m和相似系数r的优化
在计算BOLD时间序列的MSE 过程中, 若时间序列数据长度过短, 会使得样本熵不可靠, 根据Richman 和Moorman[6]的研究, 由BOLD时间序列计算样本熵时, 10m—20m的数据长度应足以估计样本熵. 对于长度较短的BOLD 信号处理中,m= 1时至少需要10—20个时间点,m= 2时至少需要100—400个时间点. 本文数据在经过预处理后得到175个时间点, 所以, 需要m值取1 或2.因此, 考虑前人研究经验(可参见2.5 节MSE)和本文数据长度, 初步将在m= 1—2,r= 0.05—0.6 以及t= 1—6 范围中寻求优化参数值.

图2 改变t, m, r 取值时, 两组样本差异较显著脑区数量 (a)—(f)在尺度因子t 分别取值1—6时, 且嵌入维数取m = 1(红色线条)和m = 2 (蓝色线条)时, 在相似系数r 取0.05—0.6 上分别计算所得的显著性脑区数量(p < 0.05); (g)尺度因子t 从1—6 各个对应的样本熵做平均, 两组被试显著性脑区数量差异(p < 0.05)Fig. 2. The number of significant brain regions when changing scale factor t, embedding dimension m and similar factor r in the MSE model: (a) t = 1; (b) t = 2; (c) t = 3; (d) t = 4; (e) t = 5; (f) t = 6; (g) average number of significant brain regions over the scale factor t (p < 0.05). Here, the similarity factor r changed from 0.05 to 0.6 with a step of 0.05 and parameter of m = 1 (redline)was fixed and m = 2 (blueline) respectively (p < 0.05).
当尺度因子t= 1—6, 嵌入维数m= 1—2时, 分别设置相似系数r= 0.05—0.6(步长为0.05)可得出老年人样本组间显著性差异较大的脑区数量(p< 0.05), 如图2所示: 首先, 从尺度因子t= 1—6 下发现:m=1计算所得差异较显著脑区数量比m= 2时多, 这一特点在大部分r取值以及平均数量(图(g))皆有体现, 这意味着m= 1较m= 2更优. 进一步, 纵观图2(a)—图2(f)分析t和r优化值, 发现图2(g)决定了r只有一个非常狭小的取值空间, 即r=0.45—0.55, 在所有尺度上存在显著性差异.
通过保持嵌入维数m、尺度因子t两个参数不变(设m= 1,t= 5), 并调节r的取值(0.05—0.6,步长为0.05)得到区分程度的分类效果, 如图3 和表1所示. 发现: 当r= 0.5时ROC 曲线处于参考线以上而且AUC 值较大(如图3(a)和图3(b)所示), 这些脑区选为对认知分数较敏感脑区; 与此相反, 由图3(c)和图3(d)可见, ROC 曲线特征和AUC 值显示了该脑区对认知分数不敏感, 也就是说, 在该脑区并不存在r值使得ROC 都处于参考线以上且AUC 值较大的标志性特征. 综合图2、图3 和表1 对分类效果的分析, 取m= 1 且r=0.5 为最优参数.
3.1.2 尺度因子t的优化
取优化参数m= 1 和r= 0.5, 调节t=1—6 变化大小得到脑区的分类效果图, 如图4 和表2 所示. 如图4(a)和图4(b)所示, 在对认知分数较敏感脑区中, 当t= 5时AUC 值较大; 在其他对认知分数不敏感的脑区中, 并不存在t值能使AUC 值取较大值(如图4(c)和图4(d)所示).因此, 取t= 5 为最优取值.

图3 相似系数r 对单个脑区分类效果的影响. 保持m = 1, t = 5 参数值不变, 调节相似系数r 从0.05 到0.6, 步长为0.05, 单个脑区ROC 曲线和AUC 值 (a)左后扣带回; (b)右颞上回; (c)右枕中回; (d)右中央后回. 图(a)和图(b)显示了对认知分数较敏感的单个标志性脑区的ROC 曲线明显高于参考线的特征和较大AUC 值, 可以当做本文的功能标记. 相反, 图(c)和(d)显示了对认知分数不敏感的单个非标志性脑区的ROC 曲线绕于参考线周围的特征和较小AUC 值Fig. 3. Sorting effects of similarity factor rby ROC and AUC value in a single brain region when the similarity factor ris setfrom 0.05 to 0.6 with a step of 0.05 and parameters of m = 1, t = 5 fixed in the MSE model: (a) PCG.L:left posterior cingulate gyrus;(b)STG.R: right superior temporal gyrus; (c) MOG.R: right middle occipital gyrus; (d) PoCG.R: right postcentral gyrus. In above two planes such as (a) and (b), a single sensitive brain area to cognitive testing score could be characted by both ROC beyond the reference line and great AUC value, therefore, be employed as a functional biomarker in this study. In reverse, a single insensitive brain area could be characted by both ROC around the reference line and small AUC value in below two planes such as (c) and (d).
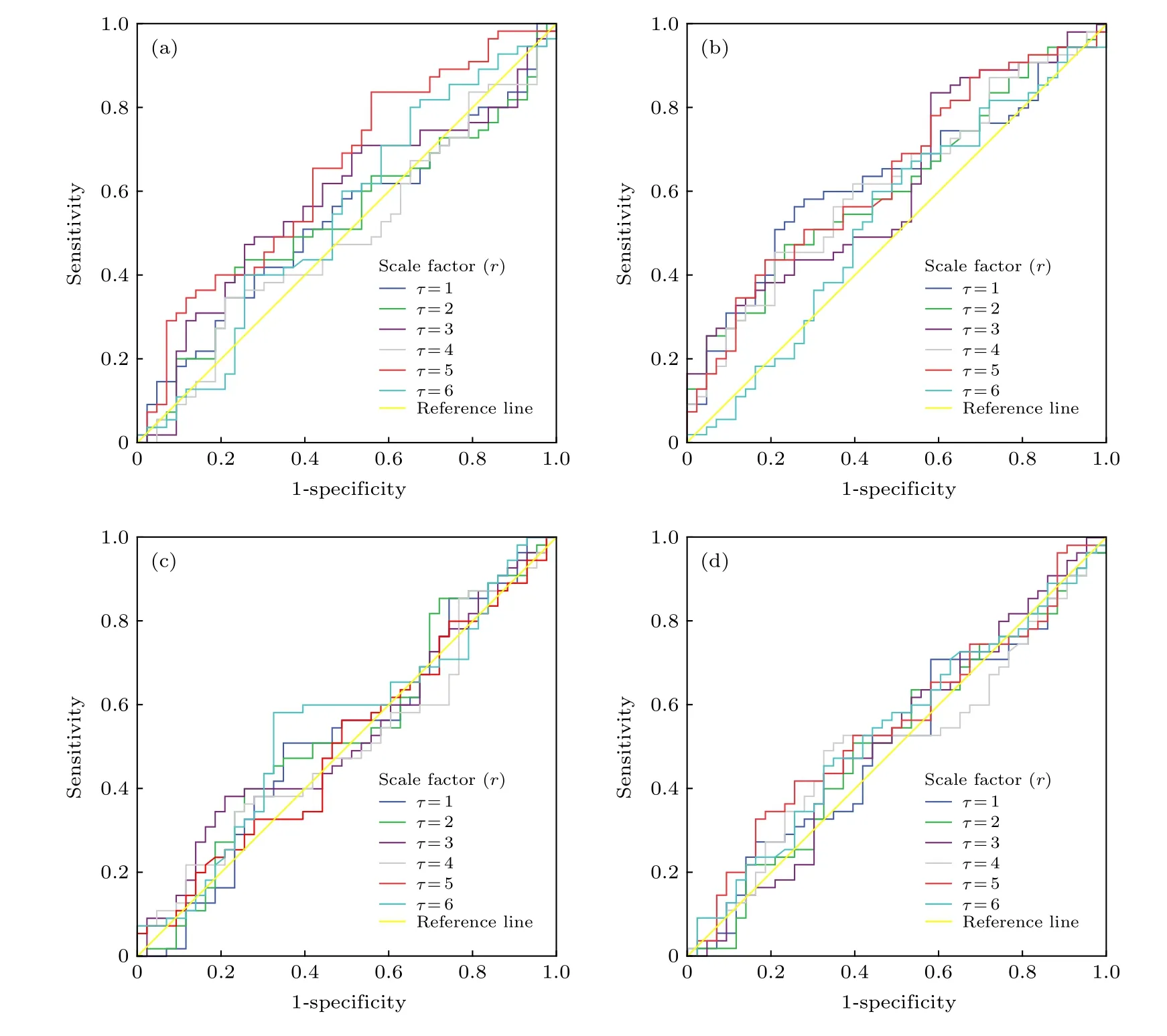
图4 尺度因子t 对单个脑区分类效果的影响. 取优化参数m = 1 和r = 0.5, 调节尺度因子t 从1 到6, 步长为1, 单个脑区ROC 曲线和AUC 值 (a)左后扣带回; (b)右颞上回; (c)右枕中回; (d)右中央后回. 图(a)和图(b)显示了对认知分数较敏感的单个标志性脑区ROC 曲线特征和较大AUC 值, 可以当作本文的功能标记; 图(c)和图(d)显示了与图(a)和图(b)特征相反的单个非标志性脑区ROC 曲线特征和较小AUC 值Fig. 4. Sorting effects of scale factor tby ROC and AUC value in a single brain region when the scale factor tis set from 1 to 6 with a step of 1 and the optimization parameters of m = 1 and r =0.5 fixed in the MSE model: (a) PCG.L: left posterior cingulate gyrus;(b) STG.R: right superior temporal gyrus; (c) MOG.R: rightmiddle occipital gyrus; (d) PoCG.R: rightpostcentral gyrus.In above two planes such as (a) and (b), a single sensitive brain area to the cognitive testing score could be characted by both ROC beyond the reference line and great AUC value, therefore, be employed as a functional biomaker in this study. In reverse, a single insensitive brain area to the cognitive testing score could be characted by both ROC around the reference line and small AUC value in below two planes such as (c) and (d).
综上所述, 根据ROC 曲线特征和AUC 值综合进行分类效果评估, 本文所取熵模型的优化参数为嵌入维数m= 1, 相似系数r= 0.5 以及尺度因子t= 5.
3.2 特征向量提取
在MSE 型的优化参数下, 即m= 1,r=0.5 和t= 5, 进行全脑熵值计算及t 检验筛选, 一共获得9个对认知分数敏感的标志性脑区(AAL)(p< 0.05), 即: 右距状裂周围皮层(CAL.R)、左内侧额上回(SFGmed.L)、左后扣带回(PCG.L)、左颞下回(ITG.L)、右颞上回(STG.R)、右楔叶(CUN.R)、 右豆状壳核 (PUT.R)、 右海马(HIP.R)、右颞极: 颞中回(TPOmid.R), 这些脑区皆 位于默认模式网络(default mode network,DMN)及周围区域. 图5 给出9个标志性脑区在优化参数下熵值集合, 从图中可读出较大分类准确效果存在颞下回等, 如图5(a)所示. 与此相反, 非标志性脑区的熵值, 如: 右中央前回(PreCG.R)、左额中回(MFG.L)、左中央沟盖(ROL.L)、左补充运动区(SMA.L)、左嗅皮质(OLF.L)、右枕中回(MOG.R)、右中央后回(PoCG.R)、左枕上回(SOG.L)、左顶下缘角回(IPL.L)等, 即便在优化参数下也没有一致性变化规律, 如图5(b)所示. 全部9个标志性脑区构成特征向量的分类效果, 如图5(c)所示, 其AUC 值可达0.808.

表1 AUC 值表达的相似系数r 对单个脑区分类效果的影响Table 1. Effect of similarity factor r on sorting rate by the AUC value of each single brain region.

表2 AUC 值表达的尺度因子t 对单个脑区分类效果的影响Table 2. Effect of scale factor t on sorting rate by the AUC value of each single brain region.
另外发现: 在优化参数取值下, 认知分数优组比差组在9个标志性脑区上的BOLD 信号复杂度要高(p< 0.05), 如图6 所示, 只有在优化参数下(即m= 1,r= 0.5 和t= 5时), 9个标志性脑区皆存在熵值的显著性差异(p< 0.05), 总体上, 认知分数优组比差组熵值要高.

图5 在优化参数下(即m = 1, r = 0.5 和t = 5)单个标志性脑区、单个非标志性脑区以及9个全部标志性脑区参与的ROC 和AUC值 (a)单个标志性脑区. 共9个; (b)单个非标志性脑区. 随机选取9个; (c)全部9个标志性脑区同时参与Fig. 5. Respective ROC and AUC value of a single indicative brain region, a single non-indicative brain regions and a total of 9 indicative brain regions at the optimization parameters of m = 1, r = 0.5 and t = 5 in the MSE model: (a)A single indicative brain region. A total of 9 indicative brain regions. (b)a single of non-indicative brain region. A total of 9 non-indicative brain regions are randomly chosen;(c) a total of 9 indicative brain regions all together.
将所有9个标志性脑区熵值取平均值后构成特征向量矩阵, 并形成训练集和测试集数据. 当取优化参数值, 即m= 1,r= 0.5 和t= 5时, 特征向量在两组样本间具有显著性差异(p< 0.001).而在r取其他值时, 均没有显著性差异出现, 如表3所列; 在t取其他值时, 也没有显著性差异出现,如表4 所列. 也就是说, 只要由非优化参数计算的熵值所产生的训练集和测试集进行分类, 无法得到较好的分类效果.

图6 尺度因子t 取1—5时全部9个标志性脑区的组间MSE 变化规律 (a)右距状裂周围皮层; (b)左内侧额上回; (c)左后扣带回; (d)左颞下回; (e)右颞上回; (f)右楔叶; (g)右豆状壳核; (h)右海马; (i)右颞极: 颞中回. (组间差异显著性: *表示p < 0.05)Fig. 6. Inter-group MSE values change with the parameter of scale factor t (from 1 to 5 with a step of 1) in a total of 9 indicative brain regions: (a) CAL.R; (b) SFGmed.L; (c) PCG.L; (d) ITG.L; (e) STG.R; (f) CUN.R; (g) PUT.R; (h) HIP.R; (i)TPOmid.R. (*p < 0.05)..
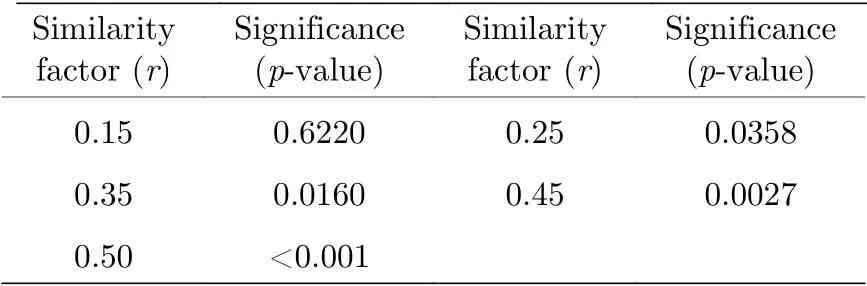
表3 几种不同相似系数r时所构建特征向量的组间显著性差异Table 3. Inter-group difference significance of eigenvectors at similarity factors(r).

表4 几种不同尺度因子t时所构建特征向量的组间显著性差异Table 4. Inter-group difference significance of eigenvectors at the scale factor(t).
3.3 ELM 分类效果及N 折交叉验证
训练集和测试集数据形成后, 将其输入ELM 进行分类.
经过ELM 分类, 可将认知分数优与差两组样本区分开, 如图7 所示, 将序号1—20 的样本分为认知分数优(类别1)和差(类别0)两类, 由图可见, 经ELM 分类后的分类准确率可达80%.
经极限学习机得出分类准确率之后, 对结果进行N折交叉验证, 在最常用的10 折交叉验证(N=10)下, 得到10 折平均分类精度为80.13%, 如表5所列.
4 结论与讨论
4.1 结 论
本文提出了MSE 模型结合现代机器学习方法, 研究了健康老年人rfMRI 熵值对认知分数分类方法. 结论: 在默认模式网络(DMN)及其周围相关区域(包括海马皮质、后扣带回、额上回和颞中回等)等9个标志性脑区熵值可对认知分数最优与最差的健康老年人群体进行认知行为分类, 分类准确率可达到80%, 说明MSE 值与认知行为密切相关, 能较有效地区分健康老年人的认知行为优劣.

图7 ELM 测试分类准确率. 通过在训练集和测试集上运行ELM 进行分类, 对认知分数优(类别1)与差(类别0)的两组样本实现约为80%分类准确率Fig. 7. Classification accuracy tested by ELM. Two groups of samples with excellent cognitive scores (Category 1) and poor cognitive scores (Category 0) could be classified at a sorting rate of about 80%.
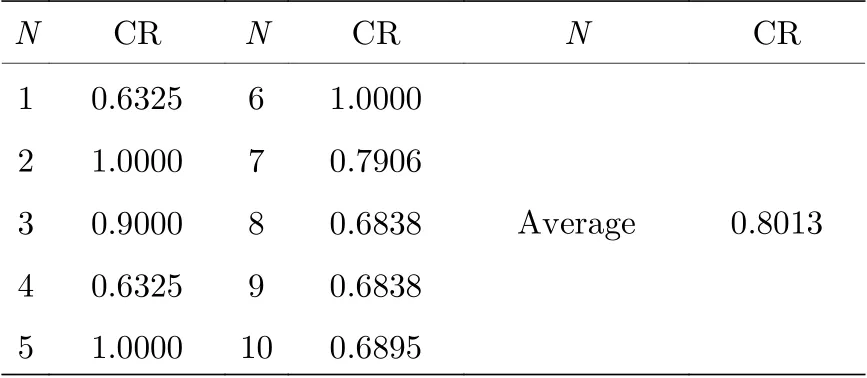
表5 经10 折交叉验证得到的分类精度Table 5. Classification rate (CR) tested by 10-fold cross validation.
4.2 熵模型参数优化
由于在以往使用MSE 处理生物医学信号时,并不具有统一的参数r,m取值标准或规范, 需要针对具体信号特征进行优化, 这就意味着优化参数来计算熵值模型时需要考虑所分析数据特征, 才可能获得更佳的分类效果. 为改进这一缺陷, 本文除了借鉴以往计算经验和rfMRI 信号特征来初步筛选参数外, 又提出并实践了诊断机器学习分类效果的ROC 曲线和AUC 值联合来确定熵值模型的计算参数, 克服了计算盲目性, 增强了参数选择的客观性, 实现了MSE 参数优化.
本文在选取计算参数时, 通过组间差异显著性联合ROC 分类效果和AUC 值较大参数值来选择老年人认知分数敏感脑区, 如图3、图4,表1、表2所示. 本文选择9个标志性脑区的特征向量给出最终分类效果, 如图7 所示, 该模型的AUC 值可达到0.808, 可见它比表1 和表2 所列单一脑区分类效果好很多. 由此可预见的是精细分割脑区将会产生更多敏感脑区, 有望提高分类精度.
对于参数t, Wang 等[31]研究fMRI 信号复杂度(使用了MSE 模型)的神经生理基础及其与功能连接的关系, 结果表明: MSE 与功能连接之间的关联取决于BOLD 信号的时间尺度或频率.Niu 等[32]也有相似研究结果, 即不同大脑区域在不同频率上表现出差异, 并认为在不同时间尺度上观察到的复杂度变化可能代表轻度认知障碍(mild cognitive impairment, MCI)和阿尔兹海默病(Alzheimer’s disease, AD)对大脑区域或网络具有依赖性的神经病理学机制. 所以, 本文选取需要分类的尺度因子t时, 经过ROC 曲线和AUC 值联合比较组间分类效果. 在标志性脑区上选择了t=5 能够将两组样本分开, 而不是在所有尺度下选取熵值.
4.3 标志性脑区的熵值
本文首先选取了在AAL 图谱中对于两组样本差异较显著脑区定义为标志性脑区, 发现这些脑区位于DMN 及其周围, 以这些脑区的多尺度熵值为特征实现了对认知能力优、劣两组健康老年人认知分数的有效分类, 拓展了熵值在功能磁共振上的应用.
Yang 等[29]发现在DMN 上BOLD 信号的MSE 值与主要认知功能(如注意、定向、短期记忆、精神控制和语言等)呈显著正相关. 同时, 也对年轻人样本与老年人的进行了对比与分析: 与年轻组相比, 老年组在左嗅皮层、右后扣带回、右侧海马、右侧海马旁回、左侧枕上回、左尾状核、左丘脑的BOLD 信号熵值显著降低, 即随着年龄增长, 大脑的这些区域的BOLD 信号复杂度显著减小. 且对于老年组, 没有发现比年轻组MSE 值有显著增加. Niu 等[32]在MCI 和AD 患者自发BOLD 信号的MSE 分析中, 分别对早期和晚期轻度认知障碍者,阿尔兹海默症患者和正常对照组等四组被试进行了检测与分析, 在4 组MSE 的单因素方差统计分析中发现: 丘脑、脑岛、舌回和枕下回、额上回和嗅皮质、边缘上回、颞上回和颞中回在多个尺度因子上都有显著性差异. 与正常组相比, MCI 和AD 患者的BOLD 信号复杂度显著降低, 而AD患者复杂度又低于MCI 患者.
4.4 标志性脑区
利用熵值评估认知行为优劣, 首要问题是寻求熵值对认知行为(本文以rfMRI 扫描前一系列量表测试获得分数来表征)敏感的标志性脑区, 本文发现的标志性脑区与以往利用功能连接选取的具有很大交集.
Raichle 等[33]首次在rfMRI 静态功能连接下发现默认模式网络(DMN)与认知功能相关; 而后,Greicius 等[34]进一步发现自发的BOLD 活动大多表现在DMN 脑区, 这些脑区表现出更显著的功能连通性, 从而提供迄今为止最有说服力的证据, 即存在默认模式网络. Buckner 等[35]在对大脑默认模式网络的解剖、功能和疾病相关性等方面进行研究时, 更具体地认为DMN 包括后扣带回、楔前叶、内侧前额叶皮质、压部后区皮质、内侧颞叶、顶下小叶和海马等区域. 在对早期MCI 和晚期MCI 研究中, Goryawala 等[36]提出了一个基于MRI 体积和神经心理学评分的统计框架, 以神经心理学参数和颞、顶叶和扣带回区的皮质体积为主要分类因素, 对早期MCI 和晚期MCI 进行分类取得了73.6%的分类准确率. 这些研究证据为本文提出的ROC 和AUC 联合诊断分类效果的方法来优化多尺度熵值模型参数, 并以此寻求对认知分数敏感的标志性脑区提供了支撑.
除此之外, 来自脑结构的研究证据与本文发现的标志性脑区也具有很大交集. 例如, Wang 等[37]研究在遗忘性轻度认知障碍者(aMCI)和主观认知衰退者(subjective cognitive decline, SCD)的脑白质网络的异常组织分析中, 发现aMCI 患者的右前扣带回、距状裂及周围皮层、豆状壳核和左前扣带回的中介中心性有显著改变. Smart 等[38]在SCD 老年人与正常同龄人相比的默认模式网络结构脑变化研究中, 发现: SCD 组相对于正在左、右尾额中区、左后中央回、右楔叶、右旁中央小叶、右距状裂及周围区域、右额中区和右颞极皮质结构变薄.
最后, 由图6 可观察出, 认知分数优组比差组熵值要高, 这一结果支持“复杂性损失”理论, 即衰老可造成人体生理信号复杂度降低[1,7]. 对rfMRI技术来说, 反映在自发BOLD 信号熵值减小, 复杂度降低的特性上, 据此推测认知分数降低与老年人认知能力下降有很大关系.
4.5 局限与展望
本文尽管给出了基于rfMRI 的MSE 值计算方法, 并结合了容易收敛到最优解的现代机器学习方法获得了较高的认知分数分类准确率, 但尚无法获知熵值模型参数是否能区分认知分数处于中段的良和一般的成绩, 有待获取相关数据进行深入研究; 其次, 目前利用熵值降低可识别健康老人认知分数降低, 但熵值模型参数是否能用来区别病理导致的认知分数降低有待研究; 最后, 本文所有被试大脑结构没有明显改变, 将来在老年人大脑结构发生改变基础上如何优化熵值模型参数是需要深入探索的问题.
