吃透题型 抓住方法

文 苏 洋

（作者单位：江苏省无锡市雪浪中学）

概率是研究随机现象的科学，随机现象在日常生活中随处可见。概率为人们认识客观世界提供了重要的思维模式和解决问题的方法，同时也为统计学的发展提供了理论基础。因此，概率的基础知识已经成为初中数学的一个重要分支。下面根据不同的题型，剖析解决概率问题的方法。

一、一步试验

例1端午节吃粽子是中华民族的传统习俗，妈妈买了2只红豆粽、3只碱水粽、5只咸肉粽，粽子除内部馅料不同外其他均相同。小颖任意吃一个，吃到红豆粽的概率是________。

【答题思路】这是典型的一次试验的问题，可以直接运用公式。根据等可能条件下概率的计算公式其中m表示事件A发生时所有可能出现的结果数，n表示一次试验所有等可能出现的结果数。

解：在这个题目中，所有可能出现的结果有10种，其中吃到红豆粽的结果数为2种，因此吃到红豆粽的概率是。

二、两步及以上试验

例2将如图1所示的牌面数字分别是1，2，3，4的四张扑克牌背面朝上，洗匀后放在桌面上。先从中随机抽出一张牌，将牌面数字作为十位上的数字，然后将该牌放回并重新洗匀，再随机抽取一张，将牌面数字作为个位上的数字，请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率。

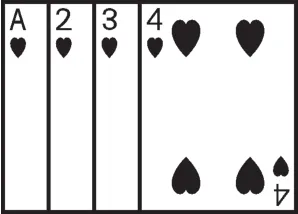
图1

【答题思路】这是一个两次试验的问题，难点在于不能直接从问题中得到答案，这时候需要借助辅助工具。同学们应该很容易想到采用列表或者画树状图的方法解决这个问题。需要注意的是，我们在读题时要分清楚是放回问题还是不放回问题。本题是放回问题。

解：根据题意，列出表格。

images/BZ_42_403_939_683_1087.png1 2 3 4 1 2 3 4 11 21 31 41 12 22 32 42 13 23 33 43 14 24 34 44

由表格可知，共有16种等可能的结果，它们出现的可能性相等；其中两位数恰好是4的倍数的有4种：12，24，32，44。所以P（两位数恰好是4的倍数）=。

或画树状图：

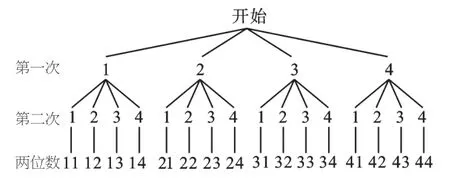
由图可知，共有16种等可能的结果，它们出现的可能性相等；其中两位数恰好是4的倍数的有4种：12，24，32，44。所以P（两位数恰好是4的倍数）=

三、几何试验

例3小红和小明在操场上做游戏，他们先在地上画了半径为2m和3m的同心圆，如图2，然后蒙上眼睛在一定距离外向圈内掷小石子，掷中阴影部分小红胜，否则小明胜，未掷入圈内不算，小红和小明获胜的可能性分别是多少？

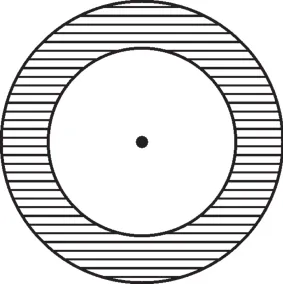
图2

【答题思路】几何试验也是一种概率模型，其特点是在一个区域内均匀分布，此时随机事件概率大小与事件所在区域的形状、位置无关，只与该区域的面积有关。几何概率试验问题一般较为简单，同学们只要根据题意直接算出面积的大小关系，进而得到正确结果。本题中同学们只需要计算出中间小圆的面积和圆环（阴影部分）的面积，即可算出两者获胜的概率。

解：内圈小圆的面积为4π，大圆的面积为9π，则圆环的面积为5π，因此小红获胜的概率为小明获胜的概率为。。