基于NARX 神经网络的船舶升沉运动实时预测方法

楼梦瑶，王旭阳*，陈瑞，葛彤

1 上海交通大学 船舶海洋与建筑工程学院，上海 200240

2 上海交通大学 海洋工程国家重点实验室，上海 200240

0 引 言

随着海洋开发活动的深入，海上作业量大幅增加。为了保证海上作业能够安全、高效地进行，需要尽量减少海浪对作业船舶的影响，降低作业风险。在海上钻探、海上拖曳、海上吊装、深海探测等作业任务中，母船受波浪影响，将带动相应的吊装拖曳系统做升沉运动，使缆绳产生巨大的附加载荷，进而缩短缆绳的使用寿命，导致深海作业装备的作业环境不稳定。因此，有必要对海上作业系统增加升沉补偿系统。虽然升沉补偿系统的效率取决于所建立模型的准确度，但是即使有了准确模型，传感器测量和控制器执行之间的时间延迟也会导致补偿效果不佳。而利用船舶运动历史数据进行升沉运动预测可以有效弥补系统延迟造成的影响[1]。

Lainiotis 等[2]讨论了船舶升沉运动估计问题，对比了3 种解决方案，认为卡尔曼（Kalman）滤波器作为线性最优估计工具，对确定的模型可以提供最优估计值，而若实际模型不能完全确定时，神经元感知器估计值则会优于传统方法，能够快速提供精确的估计值。Küchler 等[3]提出通过快速傅里叶变换（ Fast Fourier Transform, FFT）提取船舶升沉运动时间序列的幅频参数，然后利用卡尔曼滤波器进行最优估计，来快速预测母船的升沉运动。但这种方法受FFT 结果的影响较大，且FFT 适用于平稳信号，对于时变非平稳信号的分析存在较大误差，无法表示某个时刻信号频谱的分布情况。Shi 等[4]分别采用时间序列自回归（Autoregression，AR）模型、Elman 神经网络和支持向量回归（Support Vector Regression, SVR）预测算法，预测了船舶起重机的升沉运动。其中，针对SVR 参数寻优的盲目性提出了基于粒子群优化的支持向量机（SVM）预测模型，采用实验水池模拟数据进行验证，与AR 模型和SVR 模型相比，提高了预测精度。段江哗[5]提出了基于混沌理论序贯极限学习机的预报模型，在6 级海况下，预测均方根误差（RMSE）约0.15 m。陈琦等[6]提出了一种估算升沉运动位移的自适应数字滤波器，与传统滤波器相比，其提高了船舶升沉位移的估算精度，在4 和5 级海况下的最大预测偏差分别为3 及9 cm，预测结果受海况变化影响较大。

具有外源输入特征的非线性自回归(NARX)神经网络适用于时间序列预测，并已被应用于解决多种领域的非线性序列预测问题[7-8]，且NARX 神经网络对历史数据的记忆作用增强了其对动态数据的处理能力，提高了对复杂序列的预测性能[7]。本文拟利用NARX 神经网络预测母船的升沉运动，直接采用实时波高仿真值预测下一时刻母船的升沉运动值，并将该方法与普通反向传播（BP）神经网络和卡尔曼滤波预测模型进行对比。然而，海上作业不会局限于单一海况，海浪不仅会不时发生变化，而且还会遭遇风浪突然恶劣的极端情况，所以要求预测模型能够适应环境变化，以保证预测精度。因此，本文利用2～5 级海况数据建立多海况NARX 预测模型，使同一模型在不同海况下母船升沉运动均取得高精度的预测结果，以提高预测模型对海上环境的适应性和预测稳定性，减少其在实际工程应用中的潜在风险。

1 母船升沉运动模拟

船舶在海面上航行时，会受到海浪、海风、海流等因素的扰动， 升沉补偿的应用研究主要考虑海浪导致的船舶升沉运动。实际海面上，海浪是极其复杂的，它是非平稳的、不规则的随机波。为研究方便，通常将海浪假设为一个平稳随机的过程，简化为长峰波随机海浪，近似视为由无数个不同波幅和波长的微幅余弦波叠加而成。由此，随机海浪 ζ可表示为[9]

式中：n为 谐波的个数；Ai， ωi， εi分 别为第i个余弦波的振幅、角频率、初相位，而 εi是 在 0 ～2π区间均匀分布的随机变量。根据海浪频谱对随机海浪进行仿真，本文选用1964 年Pierson-Moskowitz提出的海浪谱（PM 海浪谱)，其海浪频谱Sζ(ω)表达式如下[10]

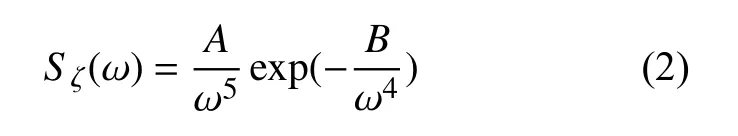
式中：A和B均为系数，A= 0.008 1g2≈ 0.78，B=0.74g/U，其中g= 9.8 N/kg，为重力加速度，U为海面上方19.5 m 高空处的风速。

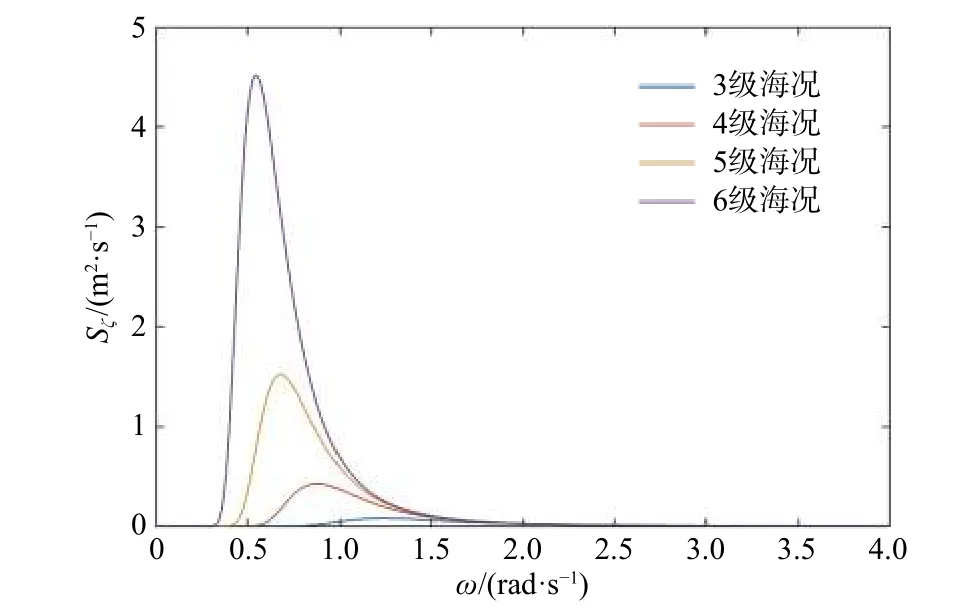
图 1 不同海况下PM 海浪谱示意图Fig. 1 The PM sea spectrum in different sea states

结合表1 中列出的各海况下的海浪参数，可以由海浪谱计算得到各海况下模拟海浪的波高时间序列值。表中，Hs表示有义波高。

表 1 海况定义Table 1 Definition of sea states

船舶对波浪的响应可通过幅值响应算子（Response Amplitude Operator，RAO）求得，RAO 是海浪波幅到船舶运动参数的传递函数，在已知波幅时间序列和船舶RAO 的情况下，可以计算得到船舶在波浪作用下的运动响应[11]。本文在挪威科技大学开发的船舶系统仿真器（Marine Systems Simulator，MSS）软件平台上实现了对母船的升沉运动仿真。母船的船型参数如表2 所示，将母船船体三维模型导入到ShipX 船舶运动响应仿真软件，获取母船水动力分析结果，将计算得到的RAO导入到MSS 的母船运动仿真模型中，实现母船的升沉运动仿真，仿真原理如图2 所示。

表 2 母船主要参数Table 2 Main dimensions of the ship

图 2 船舶运动响应仿真原理Fig. 2 The simulation principle of ship motion response

母船升沉运动仿真基于图3 中的坐标轴，其中O为坐标原点，是位于水线面中心线的中点。 本文将O点的母船升沉运动数据作为其仿真数据。图4 所示为各级海况下仿真得到的母船升沉运动时间序列。因为1 级海况下船舶升沉幅度较小，6 级及以上的海况不适合船舶出海作业，因此本文仅考虑2～5 级海况下母船的升沉运动。

图 3 坐标轴定义Fig. 3 Definition of coordinate system

2 神经网络

2.1 人工神经网络

人工神经网络是仿照生物神经元信息处理工作机制的特点建立的一种面向数据的建模技术，不需要依赖现有的数学关系式，具有表示输入与输出之间非线性关系的能力[12]。

图5 所示为基本反向传播（Back Propagation，BP）神经网络模型，它分为3 层结构：输入层、隐含层、输出层。输入层节点接受输入值并将其传递到下一个隐含层节点，在每个隐含层节点中，计算前一层节点的输出值与相应权重的乘积之和，再通过所在节点的传递函数传递至下一层节点，最后在输出层得到输出结果。

图6 为神经元结构示意图，展示了神经元节点的数据传输过程。图中：x1,x2,···,xn为第j个神经元的输入值； ω1j,ω2j,···,ωnj为输入值对应的权重；uj为输入值的加权和； θj为该神经元的偏置；yj为该神经元输出值。

神经网络中神经元节点的计算规则如下：

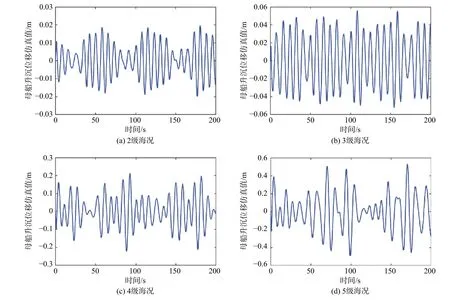
图 4 母船升沉运动时间序列Fig. 4 Time series of ship heave motion

图 5 BP 神经网络结构示意图Fig. 5 An example of BP neural network with three layers

图 6 神经元结构模型Fig. 6 The model of neuron structure

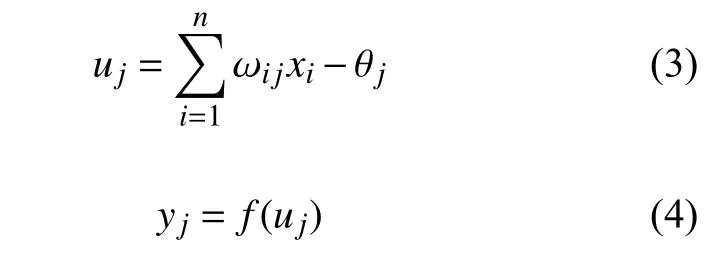
式中：i=1,2,···,n， 为神经元节点的输入数；xi为神经元第i个输入值； ωi j为神经元第i个输入权重；f(·)为激活函数。本文中所有神经元的激活函数均是双极性S 型函数。

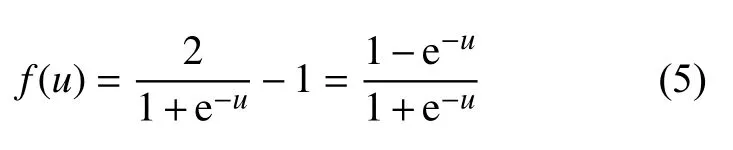
2.2 NARX 神经网络

NARX 神经网络是Leontaritis 等于1985 年提出的一种用于描述非线性离散系统的模型[13]，表示为

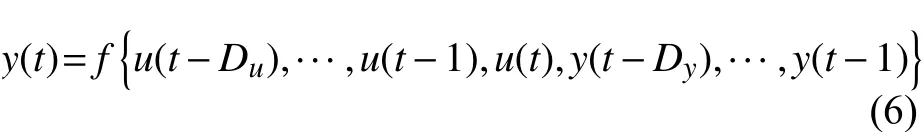
式中：u(t)，y(t)分别为该网络在t时刻的输入和输出值；Du为 输入时延的最大阶数；Dy为输出时延的最大阶数；故u(t−Du),···,u(t−1)为 相对于t时刻的 历 史输 入；y(t−Dy),···,y(t−1)为相 对 于t时 刻的历史输出；f为网络拟合得到的非线性函数。

NARX 神经网络其实是通过加入延时和反馈来模拟人脑短暂记忆的能力，是一种动态神经网络，适用于时间序列分析。与一般神经网络相比，NARX 神经网络的反馈结构和梯度下降算法使其拥有更好的收敛速度和学习效率[14]。NARX神经网络结构模型如图7 所示，包含输入层、隐含层、输出层。本文根据已测得的母船的升沉运动历史数据，预测下一时刻母船在垂直方向上的位置，来实现母船升沉运动的实时预测。所以输入层节点数根据输入值个数设定，输出层节点数根据预测值个数设定。通过合理设定隐含层层数和节点数，构建NARX 神经网络。NARX 神经网络与反向传播神经网络的训练方法类似。

图 7 NARX 神经网络结构模型Fig. 7 Structure model of NARX neural network

3 升沉运动预测仿真

3.1 不同海况下NARX 神经网络预测结果

将通过MSS 仿真模型获得的不同海况下母船的升沉运动时间序列作为预测模型的数据集。升沉运动时间序列长达200 s，数据采样时间间隔为0.05 s。将前50 s 内1 000 个数据点作为训练数据集，剩下的数据作为测试数据集。训练算法选择Matlab 神经网络模块中的Levenberg-Marquardt算法，该算法具有很好的收敛速度。针对不同海况，需要合理调整输入层节点数和隐含层节点数，选择合适的神经网络学习率，以使模型获得更高的预测精度和较快的训练速度。

本文分别对2～5 级海况下母船的升沉运动进行了预测。在预测中，利用上述各海况下母船的升沉运动历史数据，对NARX 神经网络进行了训练，并调整神经网络的网络结构和学习率，以获得最佳预测模型。不同海况下，部分预测模型的训练结果如表3 所示。表中，网络结构10-5-1 的数字依次表示为：输入层有10 个输入节点，隐含层有5 个隐含节点，输出层有1 个输出节点。其他依此类推。从表3 的预测结果中可以得出：

1） 海况等级越高，需要的延时数越多，即更需要参考历史输出。

2） NARX 神经网络在不同海况下均可满足预测精度要求，且预测误差相差不大。

3） 随着海况等级的提升，输入节点增多，神经网络的计算量自然也会增大。

图8 给出了各海况下最优NARX 神经网络的预测结果。由图可见：对于不同海况下母船的升沉运动，均可以训练得到一个合适的NARX 预测模型，预测结果和母船实际的升沉运动趋势十分吻合；只有在母船升沉运动即将发生突变的时刻，预测误差相对较大，但都在精度要求范围内，这种情况在高等级海况下更为明显。

表 3 不同海况下NARX 神经网络的预测误差Table 3 Prediction error of different sea states by NARX neural network

3.2 NARX 模型、BP 模型和Kalman 模型的预测结果对比

将不同海况下NARX 模型、Kalman 模型[3]和BP 模型的预测结果进行对比，其预测误差如表4 所示，图9 为3 种模型预测误差的直观对比结果。由图可见，Kalman 模型的预测误差远高于NARX 模型的预测误差，这与Kalman 模型中构建的状态方程的准确性有关，复杂的海浪情况实际上很难用数学公式精确表示。在低海况下，NARX模型和BP 模型的表现相差无几；但在高海况的情况下，NARX 模型的预测结果比传统时间序列BP 模型的更加稳定，精度更高。随着海况等级的增加，3 种预测模型的误差均逐渐增加，但NARX模型的误差增速最小，它对恶劣海浪环境下母船升沉运动的预测准确度更好。

3.3 多海况预测模型

预测模型应能适应复杂多变的海况，在各种海浪环境下均可稳定地实现母船升沉运动的精确预测。本文整合了不同海况下的母船升沉运动数据，作为NARX 神经网络的训练集，训练得到母船升沉运动的多海况预测模型。再利用该模型对不同海况下的母船升沉运动进行预测，并和单海况NARX 模型的预测结果进行对比。

表5 所示结果表明，多海况预测模型对于各海况下母船升沉运动的预测误差十分稳定，并没有出现随海况等级的增大误差大幅度增加的现象；且与单海况预测模型相比，多海况预测模型在2～5 级海况下的预测均方根误差分别减少了79.6%, 76.3%, 12.7%, 96.6%。由此可见，多海况预测模型的稳定性优于单海况预测模型。由图10给出的对比结果可见，多海况预测模型明显抑制了误差突然增大的现象，对母船升沉运动的跟踪效果较好。由此可以认为：多海况预测模型拥有更好的预测稳定性，可以基本适应海浪的变化。这可以减少海上作业过程中对预测模型的校正和更新，为平稳进行作业过程提供基本保障。

图 8 NARX 神经网络预测结果及误差Fig. 8 Prediction results and errors of different sea states by NARX neural network

表 4 不同模型的预测结果对比Table 4 Comparison of prediction error by different models

图 9 NARX 模型、BP 模型、Kalman 模型的预测误差对比Fig. 9 Comparison on prediction error of NARX model, BP model and Kalman model

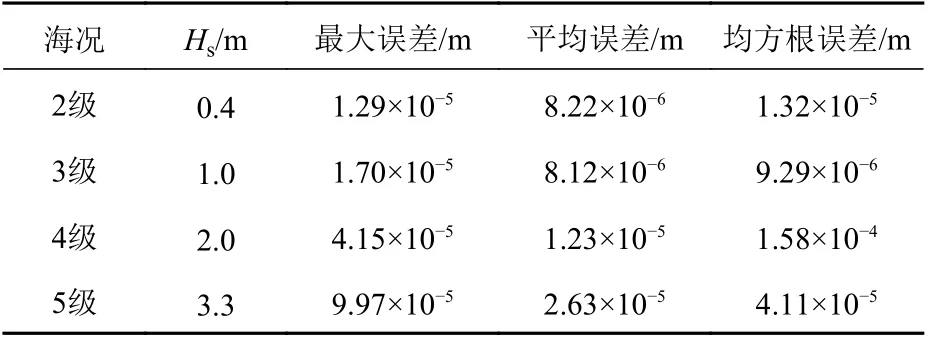
表 5 多海况预测模型的检验结果Table 5 Test results of the multi sea-states prediction model

4 结 论

本文基于NARX 神经网络建立了船舶升沉运动的预测模型，通过与Kalman 预测模型、BP预测模型进行对比，验证使用NARX 神经网络预测母船升沉运动的可行性。并且在单海况NARX预测模型的基础上建立了多海况预测模型，提高了预测模型的适用环境范围。通过仿真验证及预测结果分析，得出以下结论。

图 10 多海况与单海况NARX 模型的预测误差对比Fig. 10 Comparison of prediction error between the NARX model of multi sea-states and of single sea-state

1) 相比于Kalman 模型和BP 模型，NARX 预测模型可以获得更高的预测精度。NARX 模型在四级、五级海况下的最大预测误差分别为0.114和0.710 cm。NARX 神经网络相比传统滤波方法的优势在于不需要提前给出精确的物理模型，而是通过分析运动数据来拟合物理模型，从而进行预测。NARX 神经网络的结构特点也使得它比BP 神经网络有更好的学习效率，对复杂时间序列有更高的预测精度。

2） 多海况预测模型在各级海况下均取得了很好的预测结果，与单海况预测模型相比，大幅度减少了预测均方根误差，展现了更好的稳定性。初步认为，多海况预测模型可以适应复杂多变的海浪环境。