多领航者导引无人船集群的分布式时变队形控制

吴文涛，古楠，彭周华，刘陆，王丹

大连海事大学 船舶电气工程学院，辽宁 大连 116026

0 引 言

近年来，随着通信技术和嵌入式系统性能的快速提高，推动了无人船（USV）、无人机（UAV）和移动机器人（Mobile Robot, MR）等智能化设备的不断发展。无人船作为一种新兴的水面无人平台,得到了广泛研究[1-5]。迄今，单个无人船已可完成目标及路径跟踪和避障等任务，但面对复杂的海情，尤其是在执行军事、救援和鱼群探测等任务时，对无人船的作业效率和快速性提出了更高要求，单个无人船的能力和效率一般难以满足需要[6-9]，而需要多个无人船或集群共同执行特定的作业任务。因此，为使无人船满足更高的应用要求，开展无人船编队的协同控制及提高智能化水平有着重要意义[10-11]。

目前，在无人船编队控制领域已开发了许多控制方法，其中具代表性的有基于图论的方法[12-13]、虚拟结构法[14]、领导跟随法[15]和人工势场法[16]等。上述方法中，基于图论的方法已得到深入研究。根据领导者类型，编队控制方法通常分为2 种：一种是由轨迹导引的协同控制，另一种是由路径导引的协同控制，后者的突出优势是空间约束和时间约束可以解耦[5,17]。此外，对于编队控制问题，还开展了许多分布式会聚和分布式编队控制研究。基于上述研究，编队队形可由编队跟踪控制器来决定，具体模式包括分布式编队避碰跟踪、领导跟随等[18-21]。对于无人船集群的分布式编队控制，目前的主要研究方向是多个领航者导引的非时变队形控制，其不足之处在于，根据给定的通信拓扑只能保持队形固定，不能应需而变，即在需求改变时，需要改变拓扑结构才能实现期望的效果，缺乏灵活性。与非时变队形控制相比，多领航者导引的分布式时变队形控制方法既可使多个USV 保持固定队形，也可产生时变队形，使其具有了队形灵活易变、操作简单等特点。若不执行任务，在多领航者的导引下，无人船集群可以采取固定的队形编队；若任务需求改变，则无需改变拓扑结构即可变换为所需的队形。

本文将主要研究含有模型不确定性和未知海洋环境扰动的欠驱动USV 集群在多领航者导引下的分布式时变编队控制问题。首先，在运动学层级，基于包含策略和操纵性原理，设计分布式时变队形制导律，通过USV 间及USV 与领航者间的信息传递关系设计基本队形，该制导律根据邻居信息（位置、前向速度和航向），在给定的时变输入信号下，计算出跟随船期望的航向及前向速度；然后，在动力学层级，基于扩张状态观测器（ESO），设计USV 的前向速度和艏摇角速度控制律，以减小模型不确定性和未知海洋环境扰动带来的影响；最后，通过对级联系统稳定性的分析，证明无人船集群时变编队闭环控制系统输入状态的稳定性，并通过仿真验证方法的有效性。

1 问题描述

如图1 所示，本文考虑由M个双桨USV 和N～M个虚拟领航者组成时变编队系统。图中：pi=(xi,yi)，为第i∈M个USV 在NED（North-East-Down）坐标系XE−YE下 的 位 置 坐 标； φi为 第i个USV 在NED 坐标系下的航向角； θk为 第k∈[M+1,N]条参数化路径的参数变量。

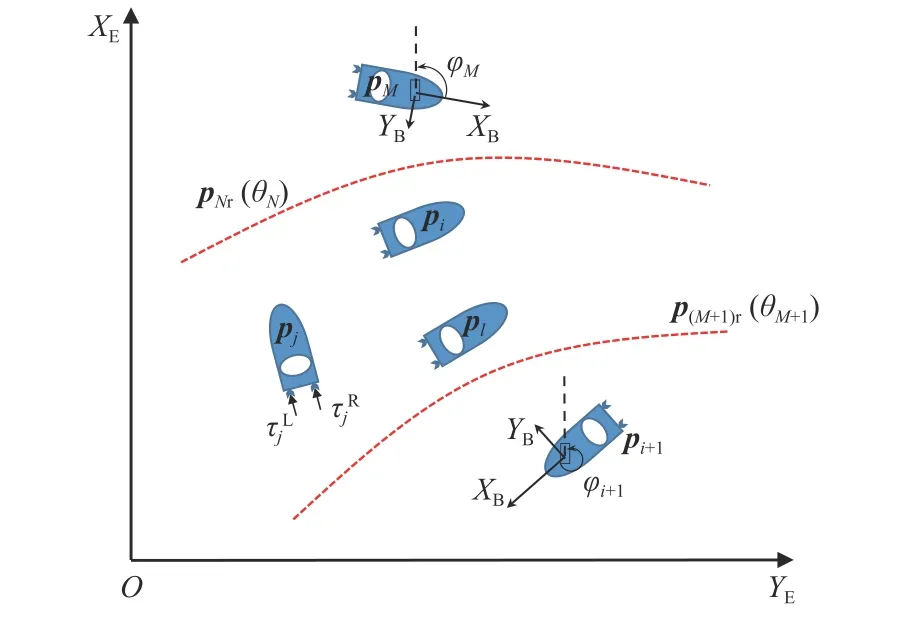
图 1 时变编队系统结构Fig. 1 System structure of time-varying formation

第i个USV 的运动学可用式（1）所示的状态方程表示[22]。

式中，ui， νi和ri分别为船体坐标系（Body-Fixed Reference Frame）XB−YB下 第i个USV 的 前 向 速 度、侧向速度和艏摇角速度。

根据无人船在水面航行时的水动力学方程，可得USV 的动力学方程如式(2)所示[23]。

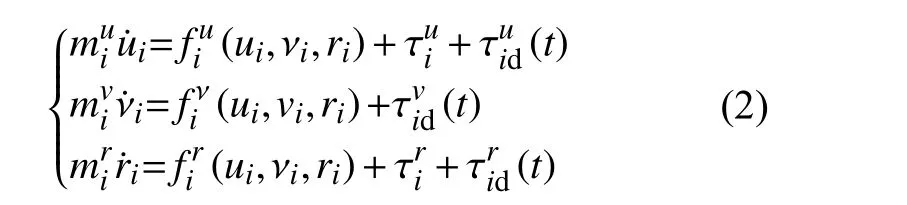
图5 和图6 表明，所有USV 在NED 坐标系下的跟踪误差在稳态时收敛到阈值以内，并在该范围内上、下波动。图7～图10 给出了USV 的实际速度与期望速度，以及实际航向与期望航向曲线。由图可以看出，基于ESO 设计的前向速度控

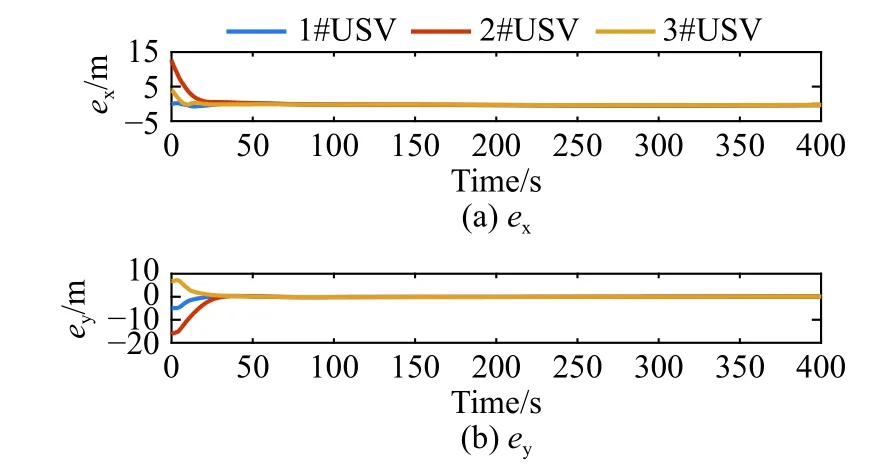
图 5 1#～3# USV 在NED 坐标系下的跟踪误差Fig. 5 1#-3# USVs' tracking error of the NED reference system

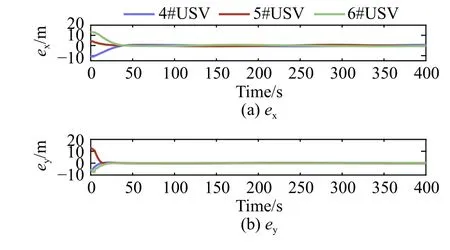
图 6 4#～6# USV 在NED 坐标系下的跟踪误差Fig. 6 4#-6# USVs' tracking error of the NED reference system

图 7 1#～3# USV 的实际速度和期望速度Fig. 7 Actual speed and desired speed of 1#-3# USV

制律和艏摇速度控制律可以使USV 在较短的时间内跟上期望值，并保持期望值运动。其中，各图中的的物理量分别表示如下：u1～u6为实际速度，为期望速度（图7, 图8）； φ1～ φ6为实际航向，为期望航向（图9, 图10）。

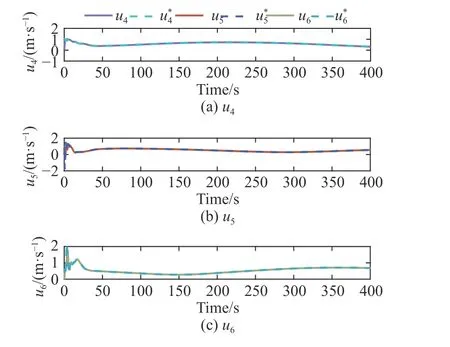
图 8 4#～6# USV 的实际速度和期望速度Fig. 8 Actual speed and desired speed of 4#-6# USV

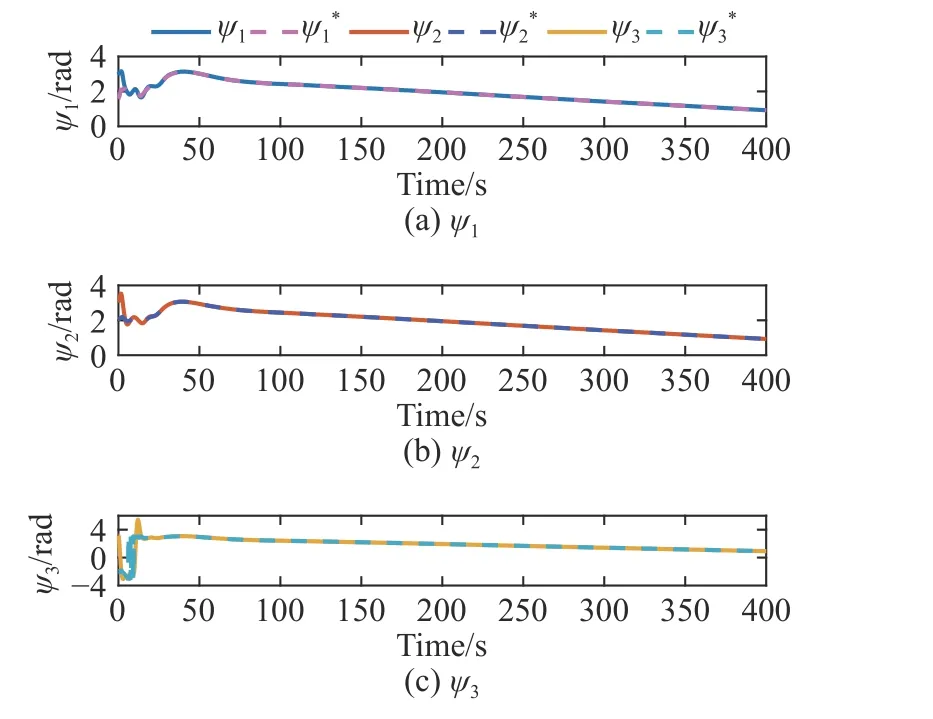
图 9 1#～3# USV 的实际航向和期望航向Fig. 9 Actual heading and desired heading of 1#-3# USV

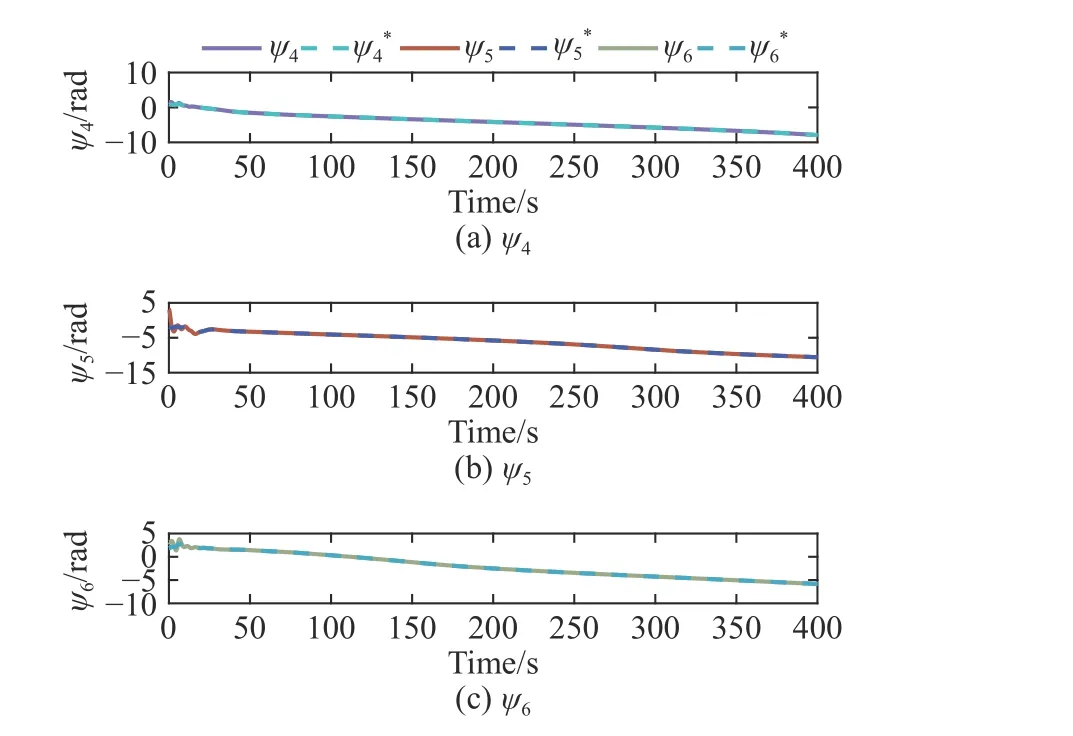
图 10 4#～6# USV 的实际航向和期望航向Fig. 10 Actual and desired heading of 4#-6# USV

图11 和图12分别给出了所有USV 在u方向推力的控制输入曲线和r方向的控制输入转矩曲线。图13 所示为2 个虚拟领航者路径参数的变化曲线。结合图4可以看出，由于给定USV 的初始位置落后于虚拟领航者，为实现虚拟领航者与USV 间的协同，路径参数以负值更新，以使虚拟领航者向USV 靠近，当与USV 接近后开始协同绕图4 所示的圆环运动。

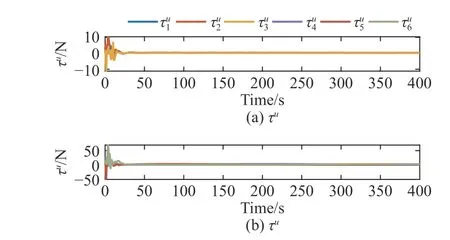
图 11 所有USV 的在u 方向的推力控制输入Fig. 11 Control input of all USVs' thrust in the u direction

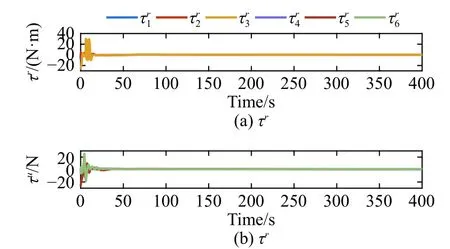
图 12 所有USV 在r 方向的力矩控制输入Fig. 12 Control input of all USVs' torque in the r direction

图 13 虚拟领航者的参数更新曲线Fig. 13 The parameter update curves of virtual leader

5 结 语

本文主要介绍了含有模型不确定性和未知海洋环境扰动时USV 集群由多领航者导引下无人船集群的分布式时变队形控制问题。首先，在运动学层级，运用包含策略和路径操纵的基本原理，设计了基于邻居信息（位置、前向速度和航向）的分布式时变队形制导律；然后，在动力学层级，设计了基于ESO 的前向速度和艏摇角速度控制律，估计了USV 在航行过程中存在的模型不确定性以及未知海洋环境扰动；最后，通过级联系统稳定性分析，证明了无人船集群时变编队闭环控制系统输入状态的稳定性，通过仿真结果也验证了该方法的有效性。