复杂流体中Janus微马达自扩散泳特性的实验研究
2020-06-03李娜娜李战华
李娜娜, 郑 旭,*, 李战华
(1. 中国科学院力学研究所 非线性力学国家重点实验室, 北京 100190; 2. 中国科学院大学 工程科学学院, 北京 100049)
0 引 言
微纳马达(Micro/Nanomotor)是一种新兴的多学科交叉技术[1-3],一般是通过化学反应等形式,将人工合成的微纳尺度颗粒所在流体环境中的化学能、电磁能等能量转化为颗粒运动的机械能[4-5]。常见的微纳马达尺寸在0.1~10 μm量级,运动速度在1~100 μm/s量级[6-7],对应雷诺数约为10-7~10-3。正如诺贝尔奖得主de Gennes所言[8],微纳马达有效的运动方式是在其周围局部流体中建立浓度场、电场、温度场等物理场,通过物理场梯度实现自驱动泳动(Phoretic self-propulsion)[9-11]。对应于所建立的浓度场、电场或温度场,自驱动泳动也分别被称为自扩散泳(Self-diffusiophoresis)[12-13]、自电泳(Self-electrophoresis)[14]或自热泳(Self-thermophoresis)[15]等。
为了建立局部的非均匀物理场,微纳马达在形式上往往由表面物理化学属性相异的两部分组成,因此也借用古希腊两面神“Janus”的名字命名。例如最常见的Pt-SiO2(铂-二氧化硅)型Janus球形微马达,在过氧化氢(H2O2)溶液中,Pt表面发生H2O2催化分解反应,产生水和氧气,使溶液中氧分子浓度升高,而SiO2侧H2O2不发生反应;在氧分子浓度梯度作用下,微马达从浓度高的Pt一侧向另一侧发生自扩散泳动。这种微马达具有加工简单、可操控性强、自发强化输运等优点,近年来受到了越来越多的关注并得到了广泛应用(微纳米机器人的动力部件[16-17]、药物输运[18-19]、生化传感器[20-21]、水污染监测及处理[22-23]、可控材料合成[24-25]等)。
对Janus微马达在简单流体溶液中自扩散泳的特征已有大量研究。如Howse等[26-27]研究了Janus微马达粒径及H2O2溶液浓度对微马达自扩散泳速度和均方位移MSD(Mean Square Displacement)的影响。作者所在课题组也系统地研究了该体系下Pt-SiO2微马达的自扩散泳特征[13, 28-29],给出了无量纲均方位移〈Δr2〉/d2随无量纲时间τ的变化关系(〈Δr2〉为MSD;d为微马达直径;τ=t/τr,t为计算位移的时间间隔,τr为旋转特征时间),如图1所示。图1中的绿色实线为微马达在纯水中的布朗运动曲线,显示出无量纲均方位移随无量纲时间呈线性变化。当微马达浸入H2O2溶液中,图1中曲线的幂次关系呈现为布朗运动、超扩散运动和类布朗运动3个阶段:
(1) 在τ<8×10-3的短时间段,由于布朗力起主导作用,微马达运动仍表现为布朗运动,均方位移随时间呈线性变化;
图1 简单流体中Janus微马达无量纲均方位移随无量纲时间的变化[13]
Fig.1 Dimensionless MSD of Janus micromotors in simple liquid varies with dimensionless time[13]
(2) 在8×10-3<τ<1的中间段,均方位移随时间的二次方增长,具有典型的弹道运动(Ballistic motion)特征,该运动幂次大于正常扩散的幂次1,称之为“超扩散运动”;
(3) 在τ>1的长时间段,微马达旋转历经各角度后,均方位移恢复线性增长规律,表现出类似布朗运动的特征,但与短时间段的布朗运动不完全相同,称之为“类布朗运动”。
已有研究大多基于水溶液等简单流体,对微纳马达在复杂流体中的运动机理及特性的研究仍然非常缺乏,已经成为近年来的研究热点[6, 30-33]。复杂流体一般具有两方面的特征:一是非均匀或各向异性的复杂分子微观结构;二是剪切应力与剪切率之间的非线性的复杂本构关系。高聚物等非牛顿流体、生物黏液等都属于复杂流体。无论是实际生物医学应用中的药物输运、生化传感,还是在复杂环境中运动的微纳米机器人,微纳马达的工作流体介质都具有复杂的流体结构,其在不同的空间、时间尺度下具有不同的动力学行为,处于复杂的几何或物理场限域中。而对复杂流体中微纳马达的运动预测及操控,都要基于对其运动特性的理解。
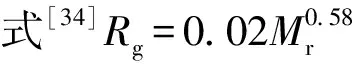
1 实验方法
本实验中使用的微马达以直径d=(2.06±0.05) μm的SiO2微球为基础制备而成。以电子束蒸发镀膜技术在微球上半表面蒸镀厚度约10 nm的Pt层,形成Pt-SiO2双面微球。制备过程如图2所示[13]。制备完成后,用刀片刮取微球并将其溶于纯水中备用。
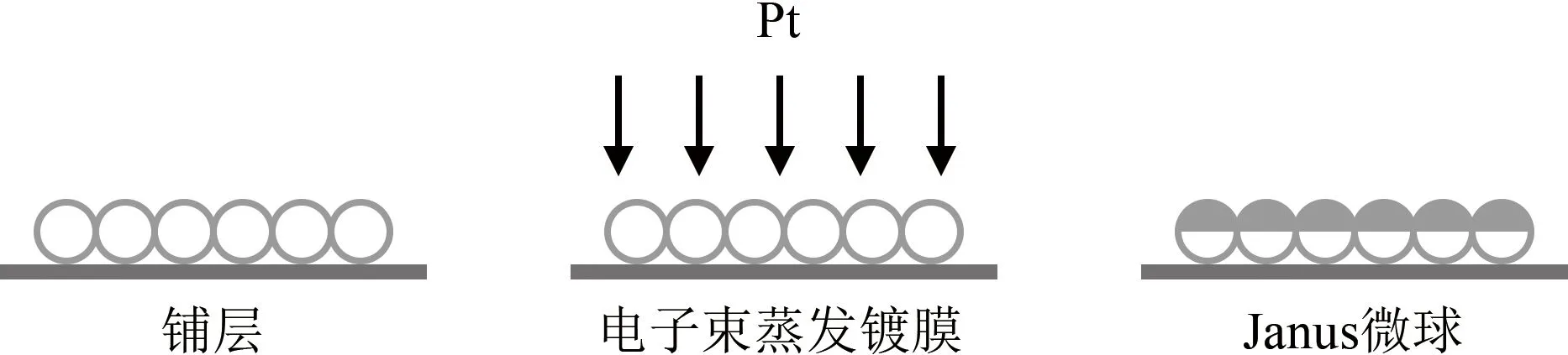
图2 Janus微马达制作过程
1.1 实验观测与图像处理
实验观测采用Olympus显微镜(配备100×/1.45物镜),以电子增益相机(Andor 897 EMCCD)进行拍摄,拍摄帧频为10~20 帧/s,图像分辨率为1024 pixel×1024 pixel。实验时,配制一系列H2O2与PEO质量分数不同的混合溶液(CH2O2=10%、15%;CPEO=0%、0.1%、0.5%、1.0%,Mr=1×105),并分别加入适量Janus微球;将溶液以微量移液管滴在盖玻片上;调节物镜焦平面位于盖玻片上方约15 μm处进行观察。对每一种工况,拍摄10~20组图像以记录Janus微马达在混合溶液中的运动;每组图像2000帧,以保证足够充分的采样量供后续统计分析。
使用图像处理软件ImageJ对图像进行优化处理,再用颗粒追踪软件Video Spot Tracker跟踪Janus微马达位置,得到每一时刻的微马达位置坐标及其运动的不规则轨迹,如图3所示。图3(a)为原始图像,微马达的黑色部分为镀Pt一侧;图3(b)为经过ImageJ重构的图像;图3(c)~(f)分别为PEO质量分数0%、0.1%、0.5%和1.0%的溶液(H2O2质量分数都为10%)中微马达的跟踪轨迹图。由图3(c)~(f)可以看到,PEO质量分数越高,微马达的运动轨迹越曲折,运动范围也越小。
Janus微马达表面的Pt和SiO2具有不同的光学性质,故其两个半球在拍摄图像中呈现的灰度值不同,这种灰度值分布不符合高斯分布,无法直接定位微马达质心。因此,使用ImageJ软件的Find Edge及Gaussian Blur等功能进行处理,重构微马达在图像中的圆形区域及其中的灰度分布;之后,通过Video Spot Tracker软件对微马达进行定位和轨迹追踪,获得不同时刻各个微马达的质心位置并计算其位移。上述处理方法对微马达质心定位可以达到半个像素的精度[13]。
1.2 微马达运动均方位移(MSD)的测量
用Video Spot Tracker跟踪微马达后,软件自动生成和保存记录每一时刻微马达位置坐标信息的数据文件。采用MATLAB对数据文件进行处理,得到每个微马达在不同时间间隔下的运动位移Δr的2个分量:

图3 图像处理与Janus微马达追踪示意图
Fig.3 Schematic diagram of images processing and particles tracking of Janus micromotor

(1)
其中,j为微马达标识,t为计算位移的时间间隔,t0为观察起始时刻。之后,对同一溶液条件下所有微马达同一时间间隔下得到的位移作系综平均〈Δr2(t)〉,即可得到系综MSD随时间t的变化。
1.3 微马达转动的测量
对Janus球形微马达转动的测量,可分别定位微球的黑半球(镀Pt一侧半球)质心O1和整个微球的质心O2,计算O1O2与x轴正向的夹角,从而确定Janus微马达的朝向角矢量φ(以逆时针方向为正),如图4所示。
再根据不同时间间隔t下微马达朝向角φ的变化量来计算转角θ:
θj(t)=φj(t0+t)-φj(t0)
(2)
之后,对同一溶液条件下所有的微马达,按照相同时间间隔t得到的转角θ作统计处理,获得该时间间隔的转角。
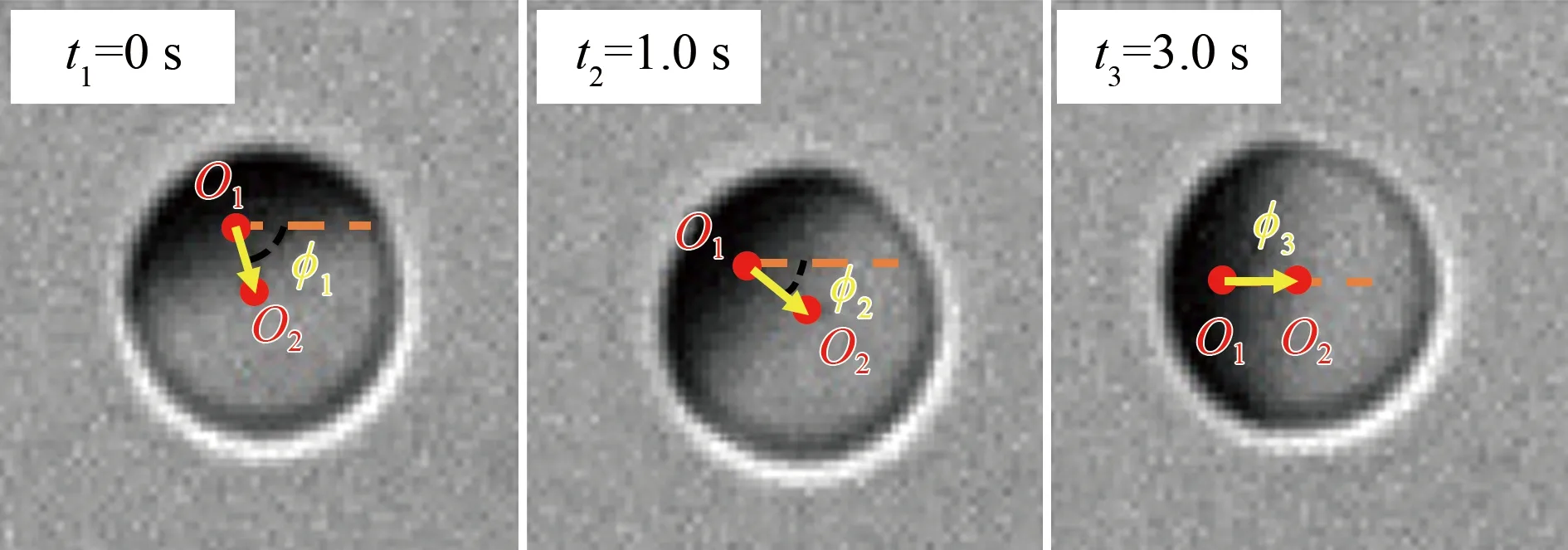
图4 Janus微马达转动测量示意图
Fig.4 Schematic diagram of rotation measurement of Janus micromotors
2 测量结果
Janus微马达自扩散泳可视作在浓度梯度作用下以特征速度u运动的平动与转动的叠加。本文测量结果给出了Janus微马达在PEO溶液中的平动和转动特征:对于平动,给出微马达的自扩散泳特征速度及MSD受PEO、H2O2质量分数的影响;对于转动,统计了微马达的均方转角并分析了其特征。从图3可以看到,实验中的微马达密度不高,相互作用可以忽略,不同微马达附近的浓度场也可视为互不干扰。
2.1 自扩散泳特征速度
通过测量一定时间间隔内(如t=0.1 s)Janus微马达的位移Δs,根据公式u=Δs/t得到微马达在PEO溶液中的自扩散泳特征速度。表1列出了不同工况下自扩散泳特征速度u随PEO及H2O2质量分数的变化,可以看到,当PEO质量分数为0%(即在简单流体H2O2水溶液中),微马达的特征速度随H2O2质量分数的增大而增大。这是因为更高的H2O2质量分数可以增强化学反应,提高微马达周围的浓度梯度。这与本课题组以往的实验结果一致[13]。当溶液中PEO质量分数提高至0.1%时,微马达的自扩散泳特征速度比在简单流体中明显降低(可降低30%左右);随着PEO质量分数增大,特征速度的降低更加明显。在H2O2质量分数为10%的溶液中,当PEO质量分数从0%提高至1.0%时,自扩散泳特征速度降低约50%。在本实验中,微观尺度上,高聚物网络尺寸ξ~C-0.76,PEO质量分数增大使得高聚物网络尺寸减小,微马达运动愈加受限;宏观尺度上,PEO质量分数增大使得混合溶液黏度增加,微马达运动需克服更大的黏性阻力,运动减弱。
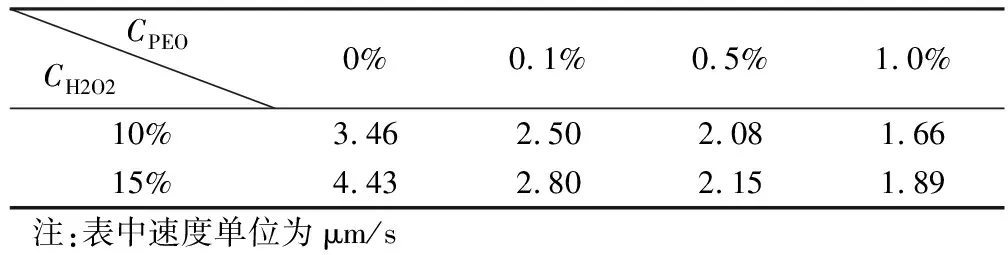
表1 不同质量分数溶液中的Janus微马达自扩散泳特征速度
2.2 PEO质量分数对微马达均方位移的影响
图5(a)给出了实验测量的微马达均方位移MSD随时间的变化情况。可以看到:在不加PEO的H2O2水溶液中(红色实线),当t<5 s时,MSD随时间变化的幂次关系迅速从起始的近似MSD~t1.0增长到超扩散的特征MSD~t1.9,幂次接近2;当t>5 s后,MSD随时间变化的幂次关系又明显减小至接近1,呈现出线性的类布朗扩散特征;而中间段和长时间段的转折发生于t=5 s附近,正好与2.06 μm微马达的旋转特征时间τr一致。依据τr与旋转扩散系数Dr的关系τr=1/Dr可计算τr,而旋转扩散系数Dr的计算公式如下:
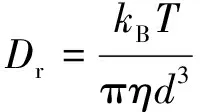
(3)
其中,kB为玻尔兹曼常量,T为热力学温度,η为溶液黏度系数(可由流变仪测出),d为微马达直径。上述三阶段(布朗运动、超扩散运动和类布朗运动)结果与本课题组在简单流体H2O2水溶液中的测量结果是一致的[13]。
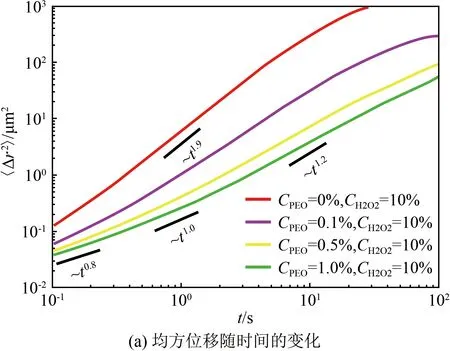

图5 10%的H2O2溶液中不同PEO质量分数时的Janus微马达均方位移
Fig.5 The MSD results of Janus micromotors in 10% H2O2solutions with different PEO mass fractions
加入PEO后,MSD曲线发生了变化。可以看到,随着PEO质量分数增大,MSD曲线相对于简单流体H2O2水溶液的结果向下偏移,这反映了溶液黏度系数η随着PEO质量分数的增大而增大,黏度的影响可以由MSD~Dt=kBTt/3ηd定性描述。此外,微马达在PEO溶液与H2O2水溶液中的MSD曲线(图1)略有不同,表现为亚扩散、超扩散和类布朗运动的三阶段特征。实验结果如下:
(1) 在短时间段出现了MSD~t0.8的现象(这种MSD随时间变化关系的幂次小于1的阶段称为“亚扩散段”),这与在高聚物溶液中测量布朗微纳颗粒的结果一致[34-35],其原因在于高聚物长链分子对微纳颗粒运动的局部限制作用。即使是自扩散泳动的Janus微马达,在短时间段由布朗运动主导时,也无法克服这种限制作用。亚扩散段之后会发展到扩散段,此时仍由随机布朗力主导微马达做布朗运动。
(2) 中间段为自扩散泳主导的超扩散阶段(即自扩散泳推进段)。随PEO质量分数的增大,幂次由接近2而逐渐减小至1.2,但仍大于1,这说明虽然质量分数增大抑制了自扩散泳的超扩散特征,但在统计上仍然与纯扩散的特征有所区别。
(3) 在长时间段,MSD随时间变化的幂次又逐渐减小到1,出现类布朗运动特征。进入长时间段的转折时刻随PEO质量分数的增大而增大,比如CPEO=0.1%时转折时刻大约为20 s,CPEO=0.5%时增大至约40 s,CPEO=1.0%时可达约50 s。
需要指出的是,上述长时间段的转折时刻仍然与考虑了黏度影响的旋转特征时间τr相近。由此,对图5(a)中的结果作无量纲化处理,以τ=t/τr为横坐标、〈Δr2〉/d2为纵坐标得到图5(b)。在本实验中,以式(3)计算τr所需的PEO溶液黏度由流变仪测量给出(对CPEO分别为0%、0.1%、0.5%和1.0%的4组混合溶液测得的黏度分别为0.9×10-3、3.6×10-3、7.2×10-3和9.0×10-3Pa·s)。在图5(b)中,可以更明显地看到各曲线的三阶段特征:
(1) 在约τ<0.03时,是短时间亚扩散段,幂次约0.8~1.0。此阶段的曲线较为重合,不同工况下Janus微马达展现出了相似的局部扩散特征。
(2) 当0.03<τ<1时为自扩散泳推进段,幂次在1.2~1.9范围内,表现出超扩散特征,仍可以看到幂次随CPEO增大而减小。虽然PEO质量分数不同的MSD增长幂次不同,此阶段的曲线显得发散,但无量纲处理的结果显示它们具有接近的起点和终点,意味着存在类似的动力学主导机制。
(3) 当τ>1时,幂次回到接近于1,为长时间类布朗运动段。无量纲均方位移均在τ>1时进入长时间段,说明微马达旋转对自扩散泳推进段截止的影响是普遍性规律,即当超越旋转特征时间后,微马达的朝向历经各角度,MSD又再次展现出MSD~t1.0的特征。在2.4节中将进一步分析转动的结果。
2.3 H2O2的质量分数对微马达均方位移影响
为说明H2O2浓度对Janus微马达运动的影响,选取PEO质量分数分别为0.5%和1.0%、H2O2质量分数分别为10%和15%时的结果进行比较。按照前述方法进行了无量纲处理,如图6所示。

图6 不同质量分数H2O2溶液中Janus微马达的无量纲均方位移随无量纲时间的变化
Fig.6 Dimensionless MSD of Janus micromotors in H2O2solutions with different mass fractions varies with dimensionless time
图6呈现出与图5(b)类似的三阶段特征。短时间段近似截止于τ=0.02处,与图5(b)的结果τ=0.03接近,意味着短时间段截止于τ=10-2量级。自扩散泳推进段与长时间类布朗运动段的转折时刻仍然位于τ=1附近。各阶段的特征可总结如下:
(1) 在τ<0.02的短时间段,不同溶液均展现出与图5(b)结果类似的从亚扩散段(幂次0.8)向扩散段(幂次1)的发展。可以注意到,蓝色虚线(CH2O2=15%、CPEO=0.5%)在更早的时刻向自扩散泳推进段转折,意味着H2O2质量分数的增大促进了浓度梯度的确立,会略微加速向推进段转折。
(2) 当0.02<τ<1时,处于超扩散段。在相同PEO质量分数下,曲线的幂次随H2O2质量分数的增大而增大,说明在PEO溶液中,H2O2质量分数增大,Janus微马达承受更强的化学反应,导致其运动加快。当PEO质量分数较小时,H2O2质量分数增大对曲线幂次增大的促进作用更为明显。
(3) 在4组溶液中,Janus微马达均在τ=1时进入长时间类布朗运动段;τ>1时,曲线呈现出MSD~t1.0特征,说明超扩散段向类布朗运动段的转折不受H2O2质量分数的影响。
2.4 转角的测量结果
在实验中,首先测量了Janus微马达转角绝对值|θ|随时间间隔t的变化。图7给出了H2O2质量分数为15%、PEO质量分数分别为0.1%、1.0%时的结果。可以看到,|θ|随时间间隔t增大呈非线性增大。短时间段内,角速度ω=d|θ|/dt≈300°/s,处于相对较快的转动状态;随着时间间隔t增大,大约在t=10 s量级时达到平台值,此时对应的角速度降低至约8°/s;还可以看到,PEO质量分数较小时,微马达的转动速度更快,尤其是在t<1 s范围。
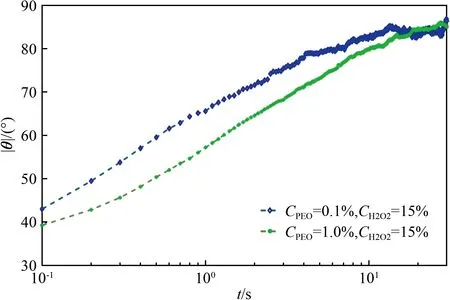
图7 Janus微马达转角随时间的变化
然后,在同一溶液条件下,使用MATLAB的hist函数对所有Janus微马达在相同时间间隔t=0.1 s下的转角θ进行统计处理,得到其转角概率分布,如图8所示。可以看到:与CPEO=0%时H2O2水溶液的概率分布曲线(绿色)相比,PEO质量分数增大到1.0%时,其转角概率分布曲线(紫色)明显展现出了偏差,即在±20°范围内的转角概率相对增大。这意味着高聚物的加入使得溶液中微马达在短时间段(t=0.1 s)内更倾向于小角度范围的转动。这一现象在Bechinger研究团队的实验中也有报道[31],他们认为这与微观高聚物长链与微球相互作用导致的转动脉动有关,但还需要更多的实验进行验证。
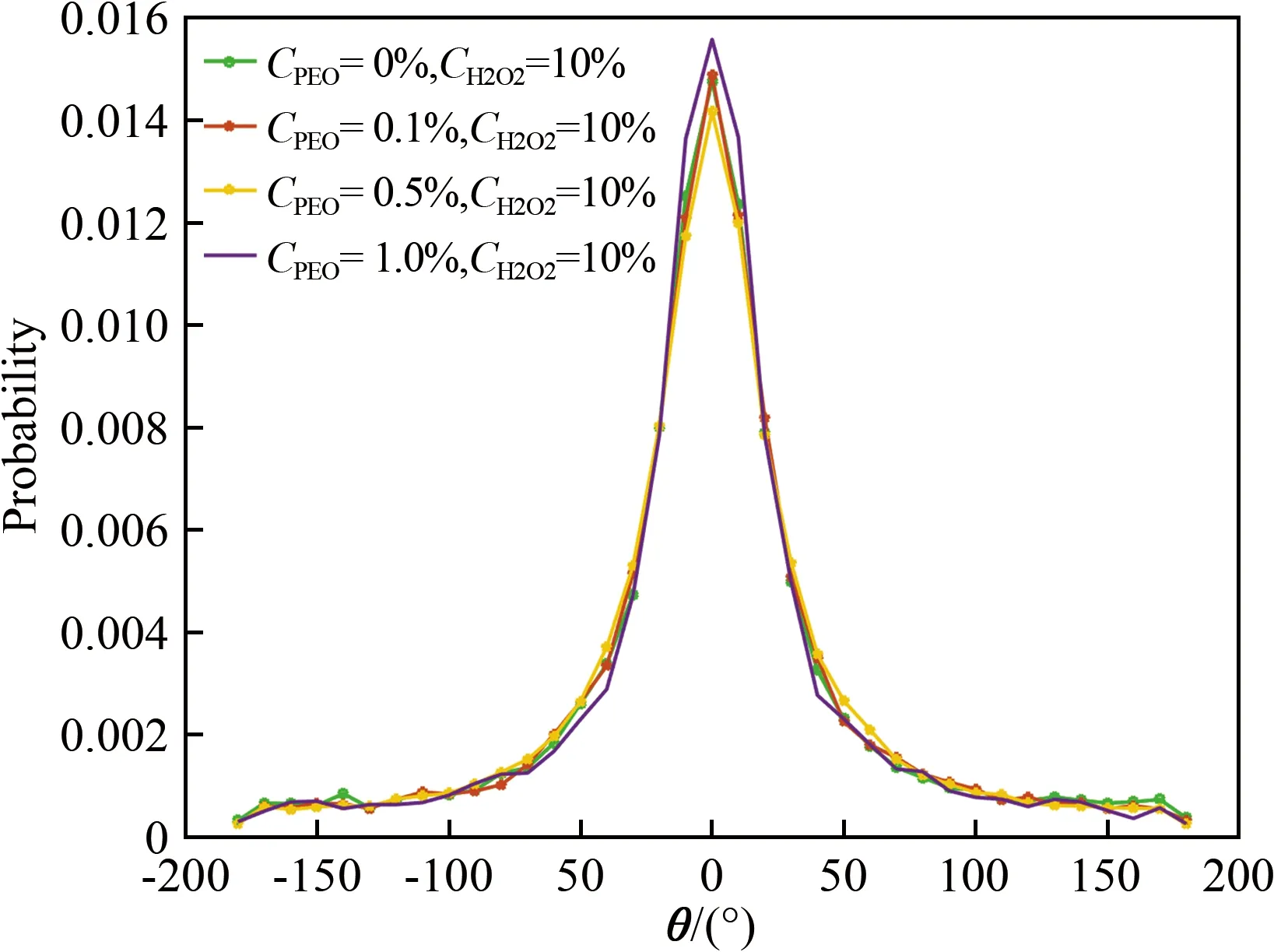
图8 t=0.1 s时Janus微马达的转角概率分布
Fig.8 Rotational angle probability distribution of Janus micromotors att=0.1 s
图9给出了测量得到的均方转角〈θ2〉随时间间隔t的变化。可以看到,均方转角〈θ2〉随时间的变化在t<1.5 s之前快速上升,而在t>2.0 s之后进入一个斜率偏小的线性段。考虑到理论上布朗转动的均方转角遵循类似平动的线性关系(即〈θ2〉~Drt),实验测量曲线呈现的两阶段斜率就意味着在短时间间隔内的大幅度转动向长时间间隔的稳定转动的过渡。由斜率估计,t<1.5 s时Janus微马达的旋转扩散系数Dr比t>2.0 s时大3~4倍。而对比图9和图5,时间间隔t约为1.5 s时的过渡时间和平动MSD的旋转特征时间τr没有对应关系。考虑到时间间隔较长时的稳定转动应由PEO溶液黏度对应的旋转扩散系数Dr主导,我们估计Janus微马达快速转动可能发生于其受限的局部高聚物网络空隙中,但相应的微观机理还需要进一步研究。
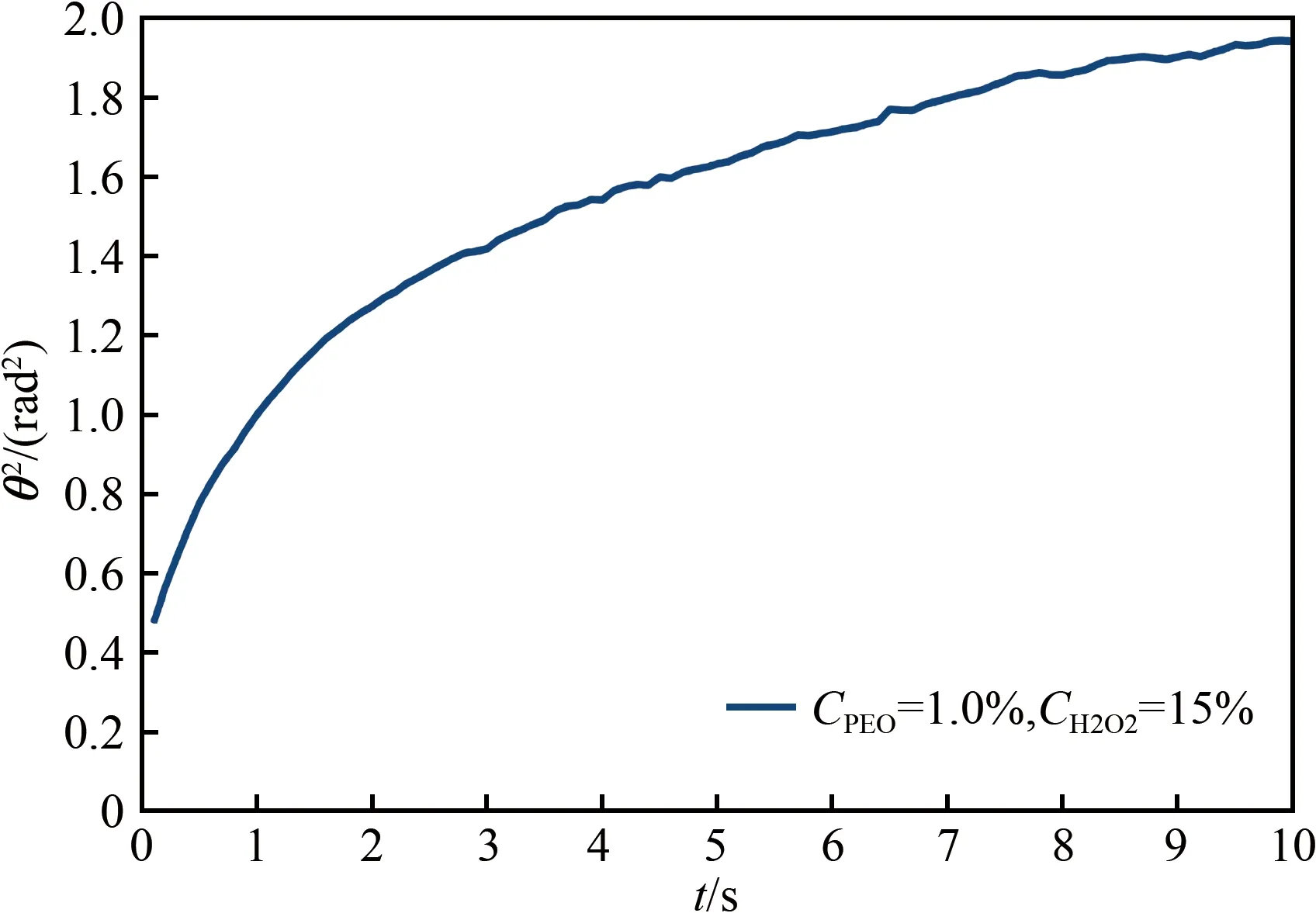
图9 高聚物溶液中Janus微马达的均方转角随时间的变化
Fig.9 The mean square rotational angle of Janus micromotors in polymer solutions varies with time
3 结 论
通过实验研究了直径2.06 μm的Janus球形微马达在不同质量分数聚氧化乙烯(PEO)溶液中的自扩散泳运动特征(实验采用的PEO质量分数范围为0%~1.0%,H2O2质量分数范围为10%~15%),分别测量了微马达的平动位移和转动角度,按不同时间间隔计算了微马达的均方位移和均方转角等,得到如下结论:
(1) Janus微马达在PEO溶液中的平动运动特征。Janus微马达的平动自扩散泳特征速度随PEO质量分数的增大而减小;无量纲均方位移(MSD)随无量纲时间的变化关系的幂次显示了高聚物溶液中Janus微马达的三阶段运动特征:τ<0.03时为短时间亚扩散段,幂次在0.8~1范围;0.03<τ<1时为自扩散泳推进段,幂次在1.2~1.9范围,并随PEO质量分数增大而减小,表现出超扩散特征;τ>1时为长时间段,幂次回到接近于1,说明微马达旋转历经各角度后会展现出类布朗运动的MSD~t变化特征。
(2) Janus微马达在PEO溶液中旋转运动的特征。与简单流体扩散理论认为均方转角随时间线性变化的规律不同,在高聚物溶液中,Janus微马达展现出短时间间隔的快速转动向长时间间隔的稳定转动转变的特征。一般认为,Janus微马达的运动可以解耦为平动和转动的叠加,转动的快慢对微马达的轨迹和在一定程度上维持定向运动的能力有重要影响。
(3) 针对实验呈现出的Janus微马达在复杂液体与简单液体中的不同运动特性,本文尝试以高聚物溶液黏性改变及内部网络结构进行解释。对于平动速度,将PEO质量分数自0%提高至1.0%,微马达的平动速度减小约50%(一方面,高聚物质量分数增大导致溶液黏度增大近10倍,运动阻力增大;另一方面,溶液中高聚物网络尺寸(ξ~C-0.76)随PEO质量分数的增大而减小,也会增强对微马达运动的限制作用);对于转动特性,加入PEO后,Janus微马达在短时间段旋转加快,这可能与微观高聚物长链与微马达相互作用导致的转动脉动有关。
(4) 在实际应用中,需考虑Janus微马达在高聚物溶液与简单液体中的不同运动特性。随着高聚物质量分数的增大,微马达的平动速度降低明显,因此对设定距离的微马达传送应适当增加驱动力。旋转运动的均方转角呈现出反常的两阶段特征,在实际应用中如需微马达运动有较高的定向性,则需抑制其转动。
