复杂网络理论下跨市场金融风险传染机制与路径研究
2020-06-02张金林孙凌芸
张金林 孙凌芸
(中南财经政法大学 金融学院,湖北 武汉 430073)
世界经济全球化和一体化进程的加快,各金融市场间的关联度不断加大。2008年,美国金融市场的过度创新诱发了区域性金融危机,世界范围内房地产市场泡沫的破灭进一步加剧了金融危机的广度和深度,最终引发全球性的金融危机。金融危机通常表现为某个国家或地区的某些金融指标发生急剧恶化,具体包括货币危机、银行危机、债务危机等,且多数情况是同时出现两种以上的危机;金融危机一旦爆发会对经济造成严重的后果,如使发生危机的国家或地区产生货币贬值、经济衰退甚至是政治动荡。当一国发生金融危机,其所产生的风险与波动扩散到其他国家的金融市场之中就形成了金融危机的传染现象。长期以来,金融危机在全球范围内频繁爆发并波及全球,越来越多的学者开始关注金融风险传染的相关研究。尤其是在东南亚金融危机发生之后,许多研究从金融危机爆发的原因、传染渠道和机制、传染后果以及危机的治理和防范等方面展开。研究发现由于任何一个国家产生的金融危机都会通过各种途径传播到其他国家并造成世界范围的影响,所以金融危机的防范与治理无法单靠某个国家完成,需要其他国家的共同努力和配合;金融危机的传染途径包括贸易渠道、金融市场渠道、季节效应以及净传染效应等,其中最主要的传染渠道为贸易与金融市场,而金融市场又包含股票市场、债券市场、黄金市场等,因此本文基于金融危机期间全球市场的经验证据对股票市场中金融风险的传染机制和路径进行研究,并期望这些研究有助于各经济主体制定更加合理有效的金融风险防范政策。
随着经济全球化的发展,金融危机在全球范围内的传播速度越来越快,全球各经济体不再是单独存在的个体,而是一个联系密切的网络,其中拓扑网络分析方法能提供有效的工具来刻画市场的网络结构与性质。利用复杂网络的相关理论,从整体的视角对金融危机的传播进行分析,可以达到全面深入研究金融危机传染路径和机制的目的。一直以来我国在全球经济活动中采取了资本管制制度和汇率管控制度,因此金融危机对我国经济影响较小;但是,由于各个国家和地区之间的贸易往来与金融投资联系日趋紧密,我国越来越难以在全球性金融危机的冲击下独善其身,因此基于金融危机期间全球市场的经验证据研究金融危机的传播具有非常重要的意义,对金融危机在国际市场中的传播机制和路径进行研究,以便在将来发生金融危机时有相应的政策措施。
一、文献综述
基于复杂网络理论对金融风险传播特性的研究成果主要集中于两个方面:一是实证分析了金融风险在金融市场网络中的传播;二是采用仿真方法对金融网络的稳定性进行研究。
利用复杂网络模型对金融市场间的风险传播进行研究,Naylor等重点研究了网络整体拓扑结构之于外汇市场的传导作用与影响,将最小生成树理论与层次树理论相结合,分别以美元和新西兰币为货币计量单位,对1995~2001年间由全球外汇市场中主要货币构成的网络进行分析,最终得出结果认为,该网络为无标度网络,且具有一定的鲁棒性[1]。Gilmore等以最小生成树及层次树研究方法为理论基础,对21个欧洲国家股票指数的互相关关系进行研究,认为在该网络中起到核心作用的是法国股市,同时发现波兰、匈牙利和捷克等金融主体之间的股票市场波动呈互相关关系[2]。Eom等以随机矩阵理论为出发点并综合最小生成树的金融时间序列股票网络拓扑性质相关知识,认为最大特征值会严重影响股票网络的形成,且股票间的信息流也会较大的影响市场效率[3]。Ulusoy等同样采用以上方法,对英国的40个主要上市公司在不同时间段的拓扑结构进行分析,得出公司所处行业会密切影响其在网络中聚集的结论[4]。黄飞雪等于2010年综合运用最小生成树与亚超度量空间相关理论与方法,分析并比较了全球主要股指在金融危机发生前后这段时间的动态稳定性和互动关系,并在此基础上考察分析了中国股票市场中的个股在上证50指数的分层结构[5]。
除此之外,部分学者采用仿真模拟方法对金融网络的稳定性进行研究。Nier通过对银行网络参数进行调整,包括资本水平、连接程度、银行间敞口规模等,分析了参数变化对传播发生概率的影响,发现发生金融危机传播的概率随着资本水平的增加而减少,随着敞口规模与集中化程度的增加而增加[6]。Muller通过在瑞士银行系统进行仿真分析,发现一旦银行系统发生危机,危机在金融系统中进行传播的可能性极高[7]。Degryse等选取国债市场进行分析,研究其对全球金融系统稳定性的影响,认为当某些国家的债务出现危机时会对全球金融系统的稳定性造成影响[8]。Raja 和Javier从国际贸易网络的角度实证分析了1990年以来历次金融危机传播的特性,得出金融危机的传播会受到危机发生国与其他国家贸易往来紧密程度的影响,当危机发生的中心国与其他国的关系越密切,危机的传播速度越快[9]。
目前已有的相关研究大多集中于利用复杂网络理论对金融市场中风险传染的存在性进行检验,以及对网络系统的稳定性进行分析,缺少复杂网络理论下跨市场金融风险传染机制与路径研究。鉴于此,本文通过选取2005~2011年期间金融危机期间全球市场的经验证据,以构建金融网络的手段,研究国际金融风险的传染机制和路径。本文的创新之处主要体现在:研究不同阶段的国际金融风险传导机制,把金融风险的传染分为三个阶段,即金融危机爆发之前、中、后时期,分别对这三个阶段的金融风险传染路径和机制进行研究;研究对象面向整个国际金融市场,有效地将复杂网络与最小生成树相关理论与方法相结合,既可以从宏观上揭示和发现系统性风险在其生成初期就在金融网络内的传染机制,也可以从微观上有效识别并重点监控系统重要性市场,进而有利于有效管控、跟踪甚至防范国际金融风险,从而为能够有效地了解国际风险传染路径、实施宏观审慎监管并防范相关风险提供一定的理论借鉴与实务指导。
二、模型设计
过去通常采用Pearson相关系数对两个时间序列的线性关系进行度量,但是两个时间序列之间往往存在着大量非线性关系,又由于实际应用中的金融时间序列呈现出非线性和异质性,简单采用Pearson相关系数法已经不能准确地度量金融时间序列之间的关系。因此,为了解决上述研究方法的不足,本文通过复杂网络分析法建立全球股票市场网络,以研究金融风险在全球股票市场中的传染机制和路径,其中最小生成树(MST)是包含某个网络中能够连通所有节点的全局极小子图,使连通全部节点的路径最短。金融危机在发生传播时很可能从被感染国家首先蔓延到关系最为密切的国家中,而从全局考虑,存在一个传播到全部节点的最短最快路径,即最小生成树图。因此,为从全局考虑金融风险在网络中传播时的应对策略,本文使用最小生成树方法对全球股票市场网络进行分析。
本文在对全球股票市场指数网络建模时,将每个指数与5个关系最密切的指数相连,产生由该指数指向这5个指数的有向边。即本文构建的全球股票市场指数网络为有向网络;由于难以获取股票市场之间的资金流动数据,本文对网络中的边不设定权重。因此,构建的股票指数网络为有向无权网络,而该有向无权网络的边指向不一定是对称的。例如,假设指数节点A与指数节点B之间有较为紧密的联系,如果B位于与A相关最密切的5个指数之中,则存在一条由A指向B的边;而即使相关系数较大,A也可能并不位于与B相关最密切的5个指数之中。那么网络中只存在A到B的边而没有B到A的边,因此网络的边有可能呈非对称指向。
(一)复杂网络统计特征描述
针对全球股票市场指数构成的网络,综合考虑数据可得性与研究可行性等问题,本文具体考察以下3个统计指标。
1.度和度分布。用ki表示网络中节点i的度,表示为与节点i连接的节点数,通常情况下越大的节点度重要性越高。根据网络是否有向分为无向网络和有向网络,后者包括出度和入度。把各个节点度进行平均就形成了网络的平均度,记为
(1)
复杂网络度的分布特征可以通过分布函数来表示。分布函数是指在网络中随机选取一个节点,其连接的边数恰好为k的概率,用P(k)表示。复杂网络中度的分布特征对判断网络的类型起到关键作用,例如泊松分布所对应的网络为完全随机网络,幂律分布则对应无标度网络。
2.直径与平均路径长度。用距离dij表示节点i和j之间最短路径上的边数。网络的直径是在网络中任意两个节点之间的最大距离,记为D,则有:
D=maxdij
(2)
平均路径长度L表示节点i和j之间距离的平均值,用N表示网络的节点数,则有:
(3)
研究发现,复杂网络中节点数越大,其平均路径长度就越小。在网络平均度
3.聚类系数。在复杂网络系统中,与同一个点关系密切的其他两个点往往不是相互独立的,这两个点之间也可能存在密切联系,这种现象就是网络的聚类特征。若用Cm表示节点m的聚类系数,Km表示与节点m相连的n个节点之间实际存在的边数,它们之间的关系表示为:
(4)
把网络中各个节点的聚类系数进行平均,得到网络的平均聚类系数C,其取值范围在0~1之间。当C的值等于0时,说明网络中所有的点都是孤立节点;当C的值等于1时,说明网络中的点与点之间都直接相连的边。平均聚类系数越接近于0,则网络整体的联系越松散,若平均聚类系数越接近于1,网络整体的联系越密切。
(二)最小生成树模型
最小生成树(MST)是网络中使全部节点的连接路径最短的连通图。金融风险的传播路径通常是从被感染国家首先蔓延到关系最为密切的国家,也意味着,存在一个传播到全部节点的最短最快路径,即最小生成树图。因此,为从全局考虑金融风险在网络中传播时的应对策略,本文使用最小生成树方法对全球股票市场网络进行分析。最小生成树图是原图的极小连通子图,包含原图中的所有节点,并且有保持图连通的最少的边,具有全局最小的权重和。MST通常采用贪心算法,针对具有n个节点的系统,从单独的节点开始,根据点之间的相似性联接各个节点,使点之间的距离组合最小且不产生回路,共生成n-1条边。
本文的全球股票指数最小生成树采用Kruskal算法(Joseph Kruskal,1956)构造,Kruskal算法的简明过程如下[10]:
1.将图中的点都看成孤立分支,将图中各边按照权值进行排序。
2.遍历图一次,找出权值最小的边,并确保此次找出的边不能和已加入最小生成树集合的边构成环。若符合条件,则将这条边加入最小生成树集合,若不符合条件,继续遍历图,寻找下一个最小权值的边。
3.递归重复步骤1,直到找出n-1条边为止(如果图中有n个结点,则最小生成树应该有n-1条边),算法结束。得到该图对应的最小生成树。设X为一个集合,则d:X×X→R如果对于任何xi,xj,xk都满足:
若d表示集合X中的一个度量,则(X,d)表示一个度量空间。满足以下性质的度量空间称为超度量空间。
对于由n个对象组成的度量空间,通过生成其最小生成树,并与度量空间关联,可以得到亚超度量空间,它是超度量空间的一种特殊形式。最早由Benzécri等发现,超度量空间是通过对n个存在某种度量距离的对象组成的集合进行分割得出的[11](P210-213)。在超度量空间中具有最好的性质、最准确的拓扑序列的空间就是亚超度量空间,并且该空间当中的拓扑序列具有唯一的指数分层结构。在建立最小生成树模型时,利用亚超度量空间能够清晰地界定亚超度量空间连接对象之间的拓扑结构,并且得到唯一确定的指数分层结构。
(三)拓扑指标
引入拓扑指标来度量网络的演化与统计性质,下文给出各个拓扑特征指标的测量方法。
1.归一化树长(NTL)定义为最小生成树(MST)网络的平均距离,是用来计算所研究在股指极端波动前、波动中和波动后的MST长度的变化。计算公式如下:
(5)
式(5)中,NTL(t)代表节点在网络里的分散程度,即网络的大小,NTL(t)越大表明节点间的连接越疏远,也体现出股票波动关联性越小。N-1表示MST网络中边数的和。
2.平均相似度(MSM)表示为:
(6)
式(6)中,D表示N×N的相似矩阵。
3.特征路径长度(CPL)是任意两个顶点i与j的平均路由个数,用来度量最小生成树(MST)网络的密集程度,即:
(7)
式(7)中,lij表示MST网络中顶点i与j之间的最短路径的边数。
4.平均占有层(MOL)是用于分析最小生成树(MST)网络的密度变化,即:
(8)
式(8)中,vi表示顶点,vc表示中心顶点,lev(vi)表示两者所在层数的差,本文把vc的层数设为0。
5.非叶子节点数(NLM)用来度量MST网络的松散程度。叶子节点是树中没有子节点的节点,即度数为0的节点,而非叶子结点则为树中度大于0的节点。
三、实证分析
(一)数据来源及处理
出于数据的可得性及代表性的考虑,本文研究的金融风险主要是指全球股票市场的风险,而全球股票市场是由全球范围内诸多国家的股票市场构建而成。在对主要股票市场进行选取时,重点考虑该国股票市场的重要性以及是否具有区域代表性,因此本文选取了2005年6月1日至2011年5月31日时段内40个国家和地区的股票市场指数,共有1481条日股票市场指数收盘数据作为经验数据。分别以金融危机爆发前后的两个时间节点(2007年6月1日、2009年6月1日)作为分界点,将每个国家的股票市场指数分为三阶段研究:(1)2005年6月1日至2007年5月31日,每个指数有499条数据;(2)2007年6月1日至2009年5月29日,每个指数有492条数据;(3)2009年6月1日至2011年5月31日,每个指数有488条数据。本文所用到的数据均取自于Wind数据库。

表1 40个国家和地区的股票市场
本文对40个国家和地区的股票指数组成的复杂网络进行建模,由于数据的可得性等原因,本文不考虑股票市场间的资金流动,只依据相关系数创建边。用Pi(t)表示指数i在t期的收盘价,t-1期为Pi(t-1),则指数i在第t期的对数收益率为Si(t)=lnPt(t)-lnPt(t-1),再通过对数收益率可计算出指数间的相关系数以及欧几里得距离。由于对数收益率是一阶泰勒级数逼近的,所以一般适用于时间间隔较短的周期,使用对数收益率的好处是可以直接相加,比如指数i从第t期到t+n期的对数收益率可以由Si(t)+Si(t+1)+Si(t+2)+…+Si(t+n)得到。此外,使用对数收益率的好处还在于其在整个实数范围内取值,在数学上便于处理。得到对数收益率以后,再利用其求出每两个指数之间的相关系数:
(9)
式(9)中的Si和Sj表示对数收益率的时间序列向量,<>符号表示某个时间序列的均值。欧几里得距离dij表示为:
(10)
(二)实证分析
根据上文中网络建模的方法,网络中每个指数节点的出度都是5,而一个节点的入度则取决于与其他节点的关系密切程度。一个指数与其他指数的关联越密切,越有可能位于其他指数的关系最密切的前五位,那么该指数节点的入度也就越大,即重要性越强。依据此方法,对各个阶段的全球股票指数网络进行建模,分别得到图1、图2和图3的网络图。
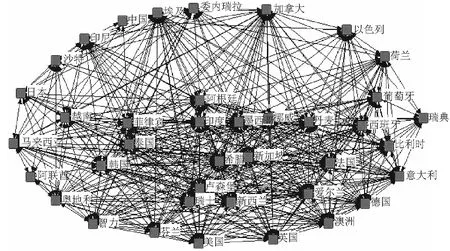
图1 金融危机前全球股指市场网络图
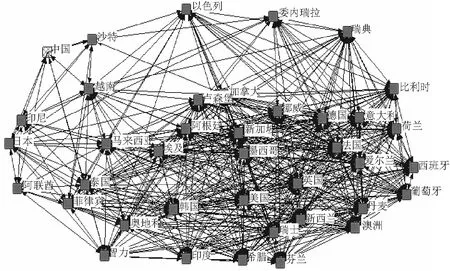
图2 金融危机中全球股指市场网络图
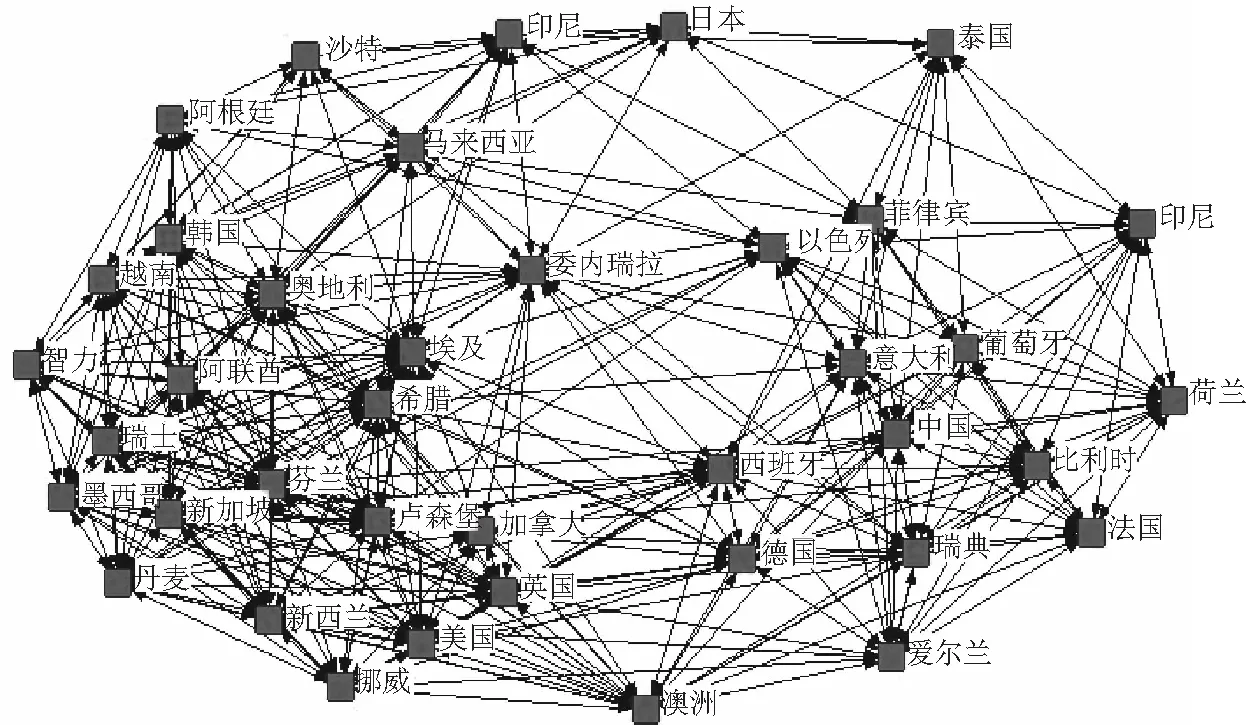
图3 金融危机后全球股指市场网络图
随后根据以上由最大度相连构建的图表计算网络中各个节点的度,并拟合度分布。本文通过表2、表3和表4依次列出金融危机前、中、后期间重要节点的度分布。

表2 金融危机前全球股指市场网络节点的度分布
从表2可以看出,在2005年6月1日至2007年5月31日期间全球股票指数市场中多数节点的度分布在中间位置,而具有较大的度的节点和具有较小的度甚至为0的节点占少部分,符合无标度网络的特征。法国股票指数(CAC40)、德国(DAX)、瑞典(OMX)、比利时(BEL20)、香港恒生、澳大利亚(S&P/ASX 200)、新加坡海峡时报等股票市场指数的度大于10,表明这些国家或地区指数与其他许多指数的关系密切,对网络中其他指数的影响较大。
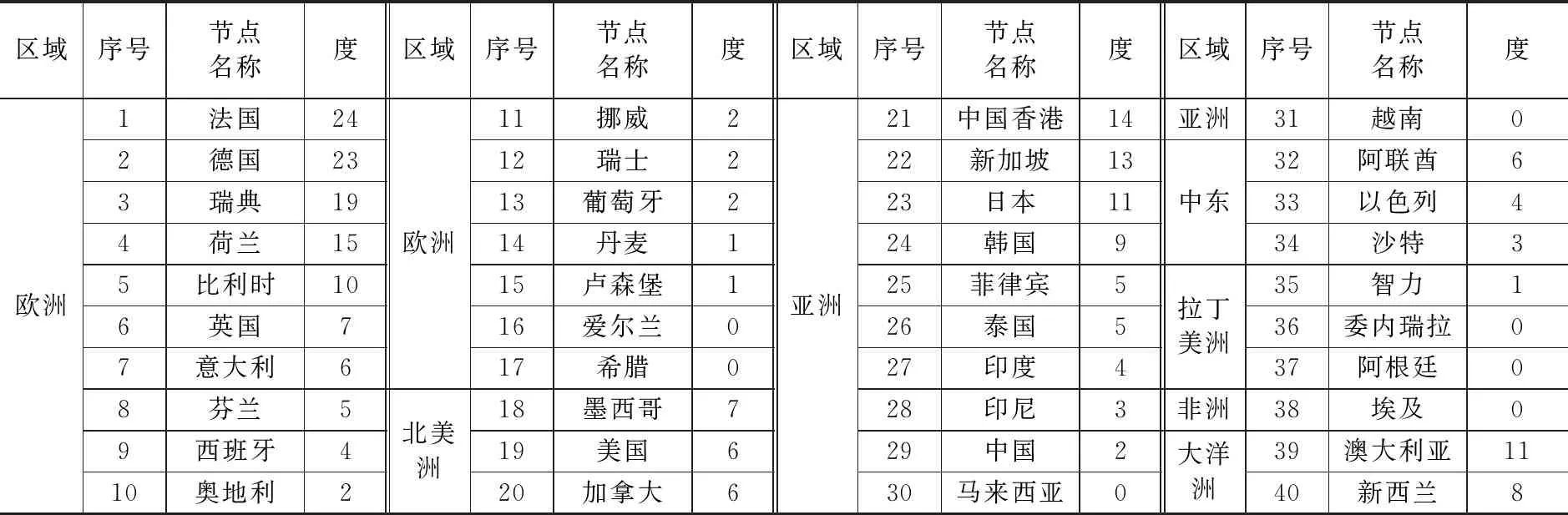
表3 金融危机中全球股指市场网络节点的度分布
从表3可以看出,在2007年6月1日至2009年5月29日期间由于全球股票指数市场中具有较大度的节点和具有较小度甚至为0的节点都占少数,而多数节点的度分布在中间位置,符合无标度网络的特征。荷兰股票指数(AEX)的度为24,是网络中度最大的节点,法国股票指数(CAC40)的度为23,位于荷兰AEX指数之后,此外还有英国(FT100)、意大利(FTMIB)、香港恒生、澳大利亚(S&P/ASX 200)、新加坡海峡时报、芬兰(HEX)、日本(Nikkei 225)等股票市场指数的度大于10,表明这些国家和地区指数与其他许多指数的关系密切,对网络中其他指数的影响较大。金融危机期间核心节点度有增加,说明各市场之间的关联度效应变强,联系更加密集。
从表3中可以看到,美国股票指数的度分布并不靠前,而是位于许多股票指数之后。这种情况似乎与现实中的认知有不符之处,本文认为产生这种现象的主要原因是:金融危机在美国起源后,通过网络的传播产生了放大效应,导致其他节点之间的互相传播起到了主要作用。例如,考虑危机从美国传播到欧洲的情况,危机首先从美国通过网络传播到了几个与其关联最密切的欧洲国家,导致这些国家发生了危机,而欧洲其他国家的指数在此之后受到的危机传播则很可能主要来自于这几个最先被感染的欧洲国家,从而使他们在网络中并不与美国的股票指数直接相连,因此造成了美国股票指数的度较低,低于起到枢纽作用的部分欧洲和亚洲国家指数的现象。

表4 金融危机后全球股指市场网络节点的度分布
从表4可以看出,在2009年6月1日至2011年5月31日期间全球股票指数市场中少数几个节点具有较大的度,少数节点具有较小的度甚至为0,而多数节点的度分布在中间位置,符合无标度网络的特征。法国股票指数(CAC40)的度为23,是网络中度最大的节点,美国标普的度为20,位于美国标普之后的有荷兰股票指数(AEX)的度为19,此外还有德国(DAX)、瑞典(OMX)、比利时(BEL20)、香港恒生、澳大利亚(S&P/ASX 200)、新加坡海峡时报、芬兰(HEX)、加拿大(S&PTSX)等股票市场指数的度大于10,表明这些国家和地区指数与其他许多指数的关系密切,对网络中其他指数的影响较大。危机之后,核心节点度下降明显,说明网络连接在金融危机之后重新变得分散。
观察表2、表3和表4发现,在三个阶段中网络中相对最为重要的节点比较稳定,荷兰AEX指数、法国CAC40指数、香港恒生指数、新加坡海峡时报指数以及澳大利亚S&P 200指数一直位于三个阶段中度最大的前十名中,尤其是荷兰AEX指数与法国CAC40指数,始终位于前列;香港恒生指数、新加坡海峡时报指数、澳大利亚S&P 200指数的排名在金融危机期间有所上升,表明在金融危机期间亚洲地区的股票指数联系更为紧密。部分指数在金融危机前和金融危机后时期都位于度最大的前十名中,但是在金融危机期间却被其他指数所取代,例如德国DAX30指数、瑞典OMX指数以及比利时BEL20指数,尤其是德国DAX30指数,在金融危机前和金融危机后都位于前列,但在金融危机期间排名大幅下降,没有位于度最大的前十名指数之中;而瑞典OMX指数以及比利时BEL20指数在金融危机期间的位置被英国FT100指数和意大利FTMIB指数所取代。
在得到网络中各个节点的度之后,可以通过对度的分布进行拟合,判断网络的类型,以便在面对危机时采取有针对性的措施进行防御。观察节点入度分布的概率P(k)与节点入度k,发现两者大致呈现幂函数关系,进行幂律函数拟合,发现危机前的2005年6月1日至2007年5月31日期间P(k)与k的幂律函数为y=0.4921x-1.439,危机中的2007年6月1日至2009年5月29日期间的幂律函数为y=0.4783x-1.469,同理,2011年6月1日至2011年5月31日期间的数据使用同样的方法进行拟合,得到危机后的幂律函数为y=0.4297x-1.403。这些现象表明,全球股指网络在各个时期都具有无标度特征。此外,发现在上文建立的网络中,我国股票市场的度始终较低,表明与其他指数的联系较弱。依据上文对数据的三段分法,分别计算这三段数据的平均聚类系数、平均距离以及直径,如表5所示。

表5 金融危机前后全球股指网络参数统计
从表5中可以发现,在金融危机发生时,网络的平均聚类系数变大,表明在危机中,股指网络在局部范围内的连接变得更为紧密,这种紧密的连接显然更有利于危机的传播。网络的平均距离变大有两种可能性,一种是来源于网络的关键节点受损,导致节点之间需要通过其他节点才能连接;另一种可能的原因是指数之间的联系变得更密切,导致原先没有连接的节点之间也产生了连接,但新产生的连接路径较长,因此提高了网络的平均距离值。在三个阶段,国际股票指数网络都具有较大的平均聚类系数和较小的平均距离,说明国际股票指数网络具有小世界特性。
(三)最小生成树分析
图4和图5表示金融危机前期和中期全球市场股票指数的最小生成树图。图中使用国家和地区名称代替该国和地区股票市场对节点进行标注。本文的分析程序采用Matlab软件编写。
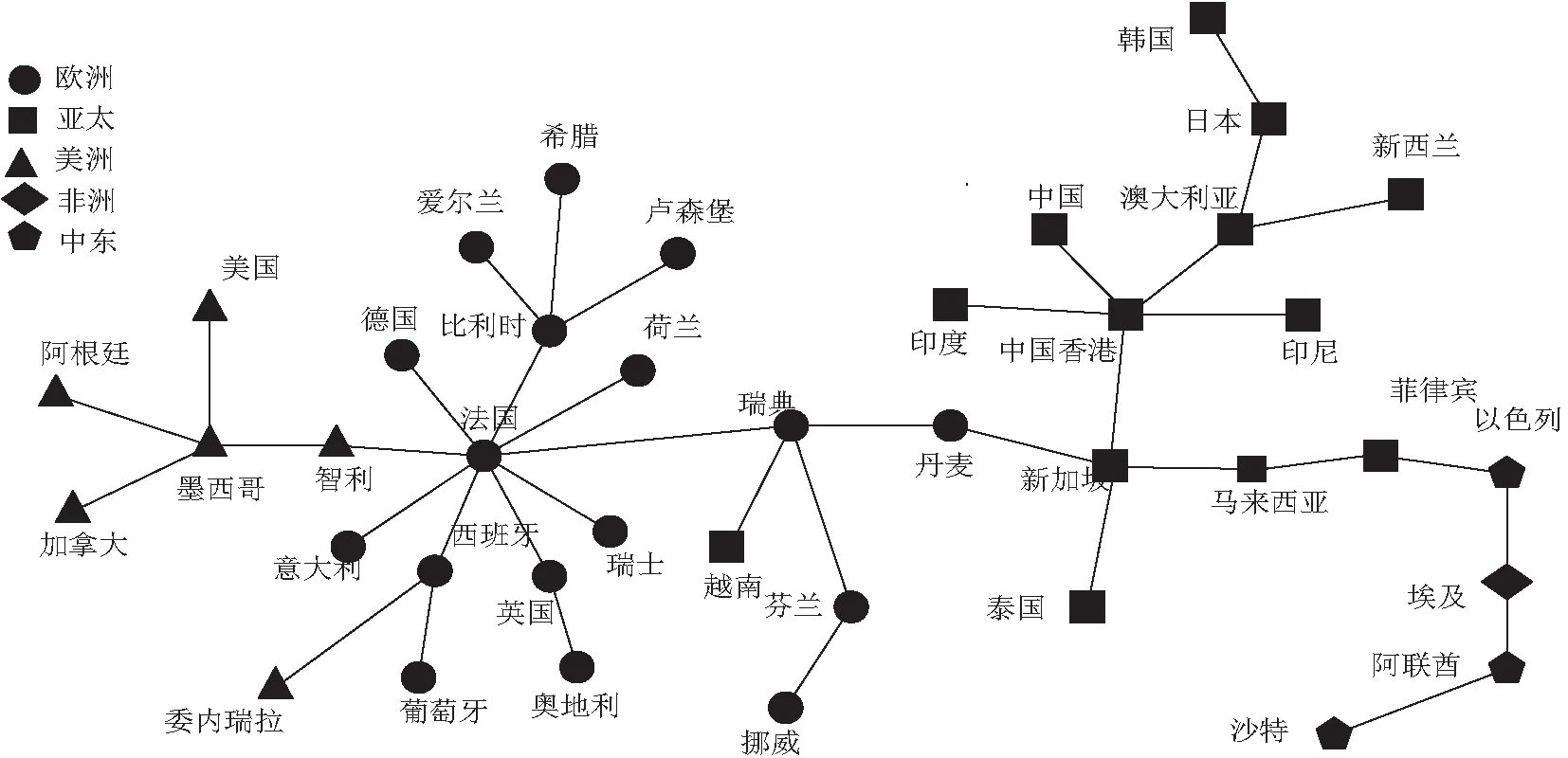
图4 金融危机前全球股票市场指数网络最小生成树
如图4所示,在金融危机之前,法国、新加坡、中国香港、墨西哥为全球股票市场网络的中心节点,通过聚集效应形成三大聚类,分别为以法国为中心的欧洲聚类、以中国香港为中心的亚洲聚类、以墨西哥为中心的北美洲聚类。欧洲聚类与亚洲聚类通过新加坡相连接。欧洲聚类效应最为显著。中国股票市场处于亚洲聚类的边缘,影响力小。
如图5所示,一些国家和地区的指数在MST网络中处于较为重要的位置,而在金融危机时期,这些核心节点的度增加,表明MST网络在小范围内的聚集效应增强,局部范围的联系更加紧密。说明在金融危机期间这些国家和地区之间的金融风险传播路径更短,传播速度快。国家和地区之间的联系在金融危机期间加强,从而加剧金融风险传染速度。

图5 金融危机中全球股票市场指数网络最小生成树
在金融危机之后,全球股票市场系统变化显著,股票市场网络得以重构。虽然欧洲聚类变化较小,保持相对稳定,但是节点度下降,网络的连接性减弱。相对于金融危机之前和其中,美国股票市场在网络中的度不断提升,在金融危机之后处于北美洲网络的中心,并直接与欧洲聚类相连接,成为网络的三个中心之一,不再处于边缘位置。亚洲聚类仍然是以中国香港为中心,并与澳大利亚市场相连接,说明不管是否发生金融危机,中国香港市场一直占据亚洲市场的中心地位。
需要说明的是,在前文中依照关系紧密度构建网络时,是从每个节点的角度考虑,只要某个其他节点与该节点关系紧密程度排在前五位,就在网络中产生一条边连接这两个节点。而在构建网络的最小生成树图时,原则是保证网络全局的权重和最小,得到原图的最小连通子图,即从网络全局的角度进行考虑。
因此,在原网络中某两个节点之间的连接如果不是最小连通子图中的边,节点之间的连接将在最小生成树图中被抹去,从而导致某些在前文依照紧密度构建的网络中处于核心地位、度较大的节点,有可能在最小生成树图中的度变得很小,处于边缘地位。同样,这也是为什么美国股票市场在最小生成树图中并不处于网络最核心位置的原因。
此外,通过研究现实世界中网络性质,发现大多数网络都具有“社区”结构,即网络中存在着聚集的“群”,处于不同群之间的节点联系相对稀疏,相同“群”之内的节点之间联系相对紧密。网络分析的重要工作之一是对“社区”结构进行识别判断,目前对网络社区结构的研究已经有较长的时间,许多方法与计算机科学中的图形分割和社会学中的分级聚类关系密切。比较成熟的算法有试探优化法(Kernighan-Lin算法)、分裂算法(GN方法)、谱平分法等。本文认为,通过最小生成树图,可以观察到网络中明显的聚集效应,符合“社区”结构定义的“群”或“团”,因此本文使用最小生成树分析的结果划分网络的社区。
分析发现不论是在金融危机之前、危机中期,还是后期,聚集效应都明显存在于全球股票网络中,这种聚集效应以地理位置区分最为显著,即可以按照地理位置划分出美洲、欧洲、亚洲三大社区。在金融危机发生时,一些核心节点的度有增加,局部范围内的密集度增加,表明网络在局部的联接呈增强趋势。与金融危机前的状态类似,在金融危机之后,大部分节点的度呈下降趋势,说明这些核心节点的影响力有所降低,网络结构更为分散。在金融危机前,网络中度最大的节点是法国,但其度从危机前的9,下降为7,再到4,表明其在网络中的重要性呈降低趋势。与之相反,荷兰股票市场的重要性在金融危机中提升显著,在危机前只与法国这一个国家相连接,到金融危机中与8个市场指数相连。美国股票市场指数在金融危机前和金融危机中都不是网络最核心的节点(原因如上文所述),但其在网络中的度始终在上升,并在金融危机后成为了网络中的核心节点。另外,中国香港一直是亚太地区最大的核心节点,说明香港特别行政区一直处于亚洲金融中心的地位。由于中国内地的资本管制和股票市场未完全开放等特征,导致中国内地的股票市场在金融危机前、中、后时期始终处于网络的边缘位置,说明中国内地股市对其他国家股市的影响相对较弱。
(四)拓扑特征分析
表6给出了金融危机之前、中、后三个时期的MST拓扑指标的数值结果。分别给出了三个时期当中归一化树长(NTL)、平均相似度(MSM)、特征路径长度(CPL)、平均占有层(MOL)、非叶子节点数(NLN)的数值结果,以用于全球股票市场网络的拓扑演化分析。
由表6可知,归一化树长与平均相似度在经历金融危机之后都有不同程度的增加。金融危机中的特征路径长度要比其他两个时期都大,表明该网络在危机时期相对其他两个时期变得松散,非叶子节点数的数值结果也印证了这一点。此外,Onnela提出平均占有层(MOL)指标越大,意味着该网络的结构稳定性就越好[12]。通过表6发现本文的MOL指标在危机发生前、后两个时期都大于金融危机发生时,说明在危机时的全球股票网络结构稳健性不如其他两个时期。

表6 MST网络拓扑指标的数值结果
表7中的Ruv表示以上5个拓扑指标的比值,表示为:
(11)
式(11)中,Lu表示时期u的拓扑指标值,Lv表示时期v的拓扑指标值。如表7所示,归一化树长(NTL)、平均相似度(MSM)、平均占有层(MOL)的比值R31都显著大于0,表明指标值在金融危机之后都有所增长,可以看出,本次金融危机对全球股票网络造成的影响巨大。平均占有层的比值R31=0.2143,次贷危机之后的值大于次贷危机之前,说明即使经历金融危机的冲击,全球股票市场网络的结构反而变得更加稳健。

表7 MST网络拓扑指标的数值比值
四、结论
本文通过对全球股票指数构建金融网络,对金融危机发生之前、中、后时期全球股市金融风险传染机制进行了研究。将每个指数与其相关程度最大的5个指数相连构成网络,画出网络的结构图,统计了各个指数节点的度,并通过对度分布的拟合,判断网络是否具有无标度特征,随后通过网络的聚类系数分析和距离统计判断网络是否具有小世界特性。实证结果表明:(1)全球股票市场具有典型的小世界特征,各国家和地区股票市场之间信息的传导是高效的,不同国家和地区股票市场之间存在着相互传导关系;(2)金融危机期间各国和地区股票市场之间的关联程度显著加强,受金融危机的影响,股市泡沫破灭,投资风险骤增,避险情绪蔓延,各国投资者对市场信息变得更加敏感,使得一个国家的波动会迅速引起其他国家的连锁反应。
随后使用从物理学科衍生出的最小生成树方法分析网络的特征,发现节点间具有明显的地理聚集效应;找出在金融危机前、中、后三个阶段中,在网络中都处于核心地位的重要节点,通过对这些节点度的分析,发现部分节点的度在金融危机发生时增加,表明网络的联接效应呈现局部增强的特点,其中度最大的节点主要来自于欧洲和亚洲,若采取措施对来自欧洲地区的荷兰、法国、英国和意大利以及来自亚太地区的中国香港、澳大利亚和新加坡等股票市场进行目标免疫,可以有效阻断金融风险的传播。而在金融危机后,大部分节点的度呈下降趋势,说明全球股票市场网络的集中度下降,核心节点的影响力减弱,同危机前的状态相似。通过以上的分析还发现,网络中的重要节点是有可能发生改变的,因此在真实运营中应该对全球股票指数网络的状态进行及时的更新和追踪,从而防范金融风险的传导。最后本文引入拓扑指标来度量网络的演化与统计性质,发现经过金融危机之后,全球股票市场网络重新构建,形成更加稳健的网络体系。
