基于不同干旱分区的土壤墒情自动监测站精度改进探究

2020-06-02张敏

水利技术监督 2020年3期

张敏

(法库县农业技术推广与行政执法中心，辽宁沈阳 110400)

近些年来，土壤墒情自动监测技术逐步在国内得到应用，其技术的发展对于区域旱情的自动监测和预警十分重要[1]。但是由于土壤含水量影响因素较多，使得土壤墒情自动监测精度一直不高，很难在区域实际旱情监测中得到应用和推广[2]。为提高土壤自动墒情监测的精度，许多学者展开其误差修正的探讨[3- 9]，通过建立土壤自动墒情监测数据和人工测定的土壤墒情数据进行回归分析，基于回归方程对墒情进行修正和改进，被许多旱情研究的学者认为是当前行之有效的方法，并在一些地区得到应用[10- 15]，但是该方法在辽宁地区还未得到相关应用，辽宁省属于全国典型的干旱区域，旱情对区域农业经济影响程度较大，为此需要建立精度较高的土壤墒情自动监测方法，提高区域旱情监测预警的时效性。为此本文主要以辽宁地区为研究实例，对辽宁省不同干旱分区的土壤墒情自动监测站精度改进对策进行分析，研究成果可为辽宁省自动墒情监测提供重要的误差修正方法。

1 土壤墒情自动监测数据修正方法

应用最小二乘法对土壤墒情自动监测数据进行回归修正，建立的回归方程主要表达式为：

θv=av2+bv+c

(1)

式中，θv—土壤墒情监测值，%；v—传感器输出电压，V；a，b，c—回归方程的变量系数。

在进行数据修正后，通过对比人工测定土壤含水率数据，分析修正误差，从而分析其修正后的土壤墒情自动监测的精度，当误差绝对值小于5%，符合测定要求，误差计算方程为：

(2)

式中，xi—土壤墒情自动监测的含水率，%；ai—人工测定的土壤含水率，%；N—对比试验的次数。

2 实例应用

2.1 辽宁省干旱概况

辽宁省干旱主要分为3个分区，分别为辽宁西部、辽宁中部以及辽宁南部地区，辽宁西部地区年降水量在400～600mm之间属于水资源相对贫乏的区域，农作物产量相对较低，一般较易发生春旱，农作物正常需水量维持在300～450mm之间。辽宁中部属于平原地区，年降水量在500～650mm之间，由于地势较为平坦，因此其土壤较为肥沃，地下水量补给也较为充足。该区域为辽宁省的主要粮食产区，也是城市工业集聚地，用水量较为紧张，一旦出现旱情，农业经济损失程度较大。辽宁南部较易出现干旱的主要为大连区域，位于辽东半岛的南部，年降水量在550～750mm之间，年降水量较为充沛，但径流深一般在150～250mm之间，水资源量较为紧张，而大连作为辽宁南部沿海重要的工业型大城市，其农业、工业以及城市生活用水矛盾日益突出，一旦发生干旱，对于大连区域影响也较为明显。

2.2 相关性分析

结合3个分区典型干旱监测站点的自动墒情监测数据分析各数据类型，结果见表1—3。

从表1中可看出，不同深度下的自动墒情监测数据和人工观测数据相关性总体低于0.5，随着深度的增加，其相关系数有所增加，表中20cm自动B以及30cm自动B为采用日均值处理后的土壤自动墒情观测值与人工观测数据的相关性分析结果，从表1中可以看出，通过日均值处理后，其相关系数相比于处理前有所增加，这是因为采用日均值处理后，其误差得到一定程度的均化，使得其相关系数有所增加。表2为辽宁中部地区土壤自动监测墒情与人工土壤含水量的相关性分析结果，相比于辽宁西部地区，其相关系数有所减小，这主要是因为辽宁中部地区土壤含水量变化影响因素较多，因此其相关系数有所减小。而对于辽宁南部地区而言，其相关系数进一步降低，这是因为辽宁南部受气候变化影响较大，干旱发生程度有时高于辽宁西部及中部地区，土壤含水量影响因素更为复杂，使得其相关系数相比于其他2个地区更有所减少。

2.3 自动墒情数据误差统计结果

结合墒情监测数据，对各干旱分区其与人工观测数据之间的误差进行统计分析，统计结果见表4—6，并对其误差直方分布进行分析，结果如图1所示。

表1 辽宁西部地区自动土壤含水率与人工观测数据相关性分析结果

表2 辽宁中部地区自动土壤含水率与人工观测数据相关性分析结果

表3 辽宁南部地区自动土壤含水率与人工观测数据相关性分析结果

表4 辽宁西部地区土壤墒情自动监测的误差统计结果单位：%

表5 辽宁中部地区土壤墒情自动监测的误差统计结果单位：%

表6 辽宁南部地区土壤墒情自动监测的误差统计结果单位：%

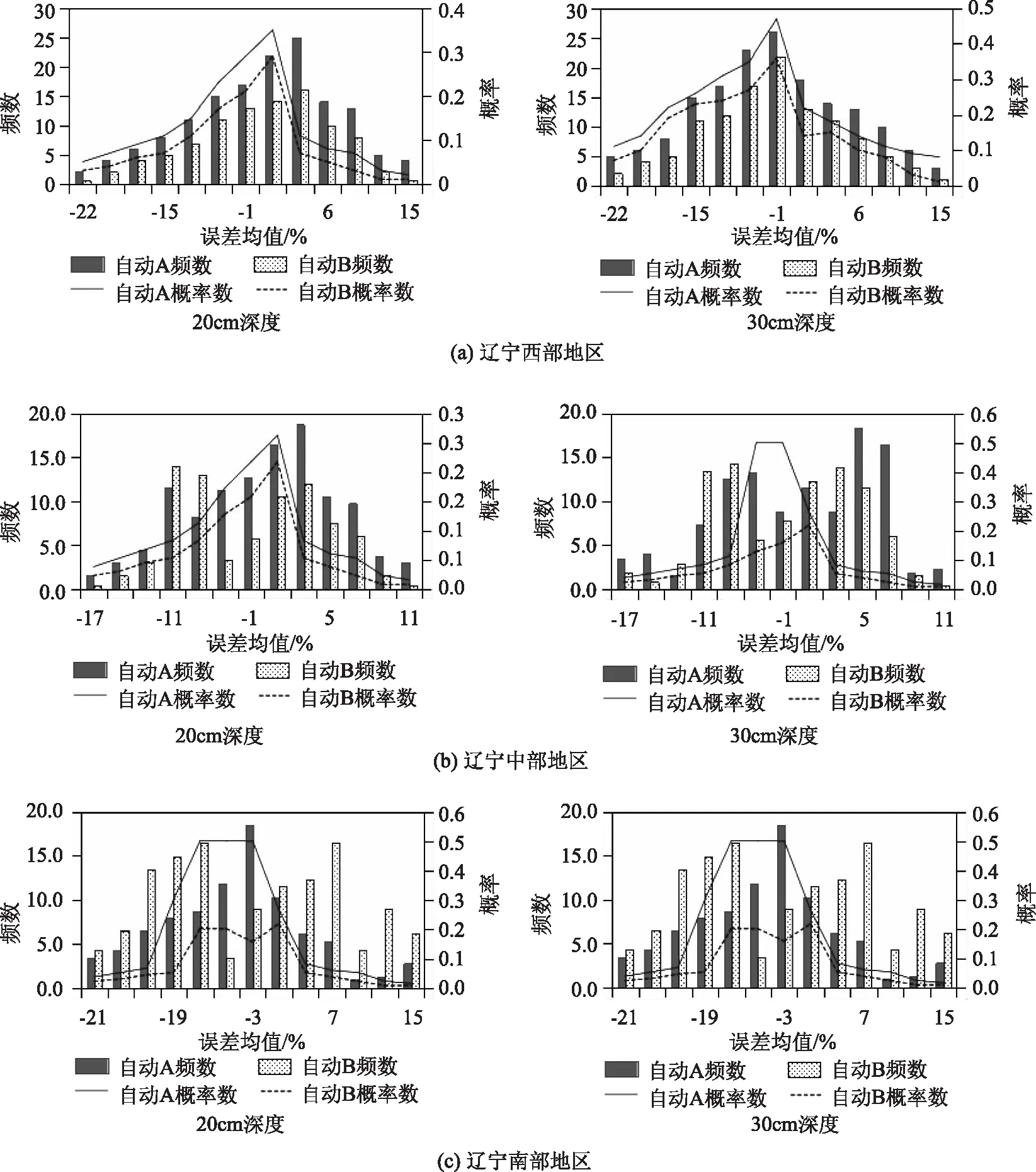
图1 各干旱分布不同土壤深度下的误差直方分布结果

从误差统计分析结果可看出，20、30cm深度下自动墒情监测数据的绝对误差均在20%以上，且各干旱误差最大值在33.08%～84.71%之间，最低值在-24.60%～-47.36%之间，可见各干旱分区不同深度下的误差均较大，且不能有效满足土壤墒情监测的规范要求。分析其误差来源，主要受到土壤不同深度含水量的变化影响，在深度20和30cm处的土壤含水量纵向及侧向变化较大，使得其土壤含水量自动监测难度较大，此外土壤自动墒情监测频数及频率对误差均值影响也较大。从辽宁西部地区误差直方分布结果可看出，当频数为25，概率为0.3时20cm深度下误差直方最小，30cm深度下频数为28，概率为0.45时误差直方最小。而对于辽宁中部地区，当频数为18，概率为0.3时20cm深度下误差直方最小，30cm深度下频数为22，概率为0.50时误差直方最小。在辽宁南部地区，当频数为15，概率为0.5时20、30cm深度下误差直方均最小。

2.4 误差修定曲线

结合各干旱分布典型土壤墒情自动监测数据，建立不同分区各干旱深度下的回归方程，见表7，并制定不同分区的误差修订曲线，结果如图2所示。

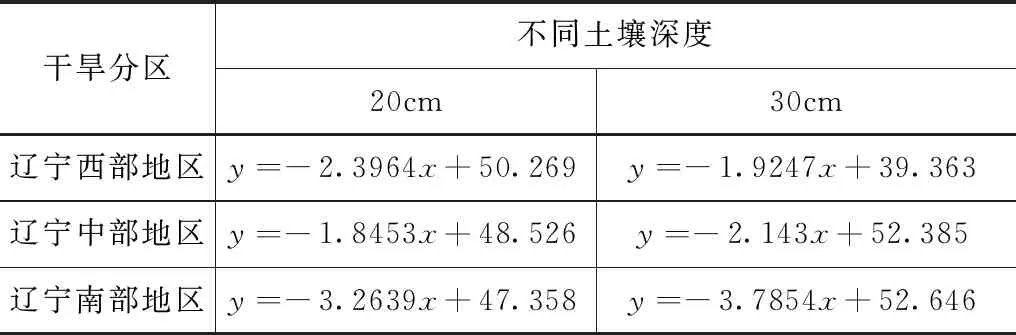
表7 各干旱分区误差修订回归方程

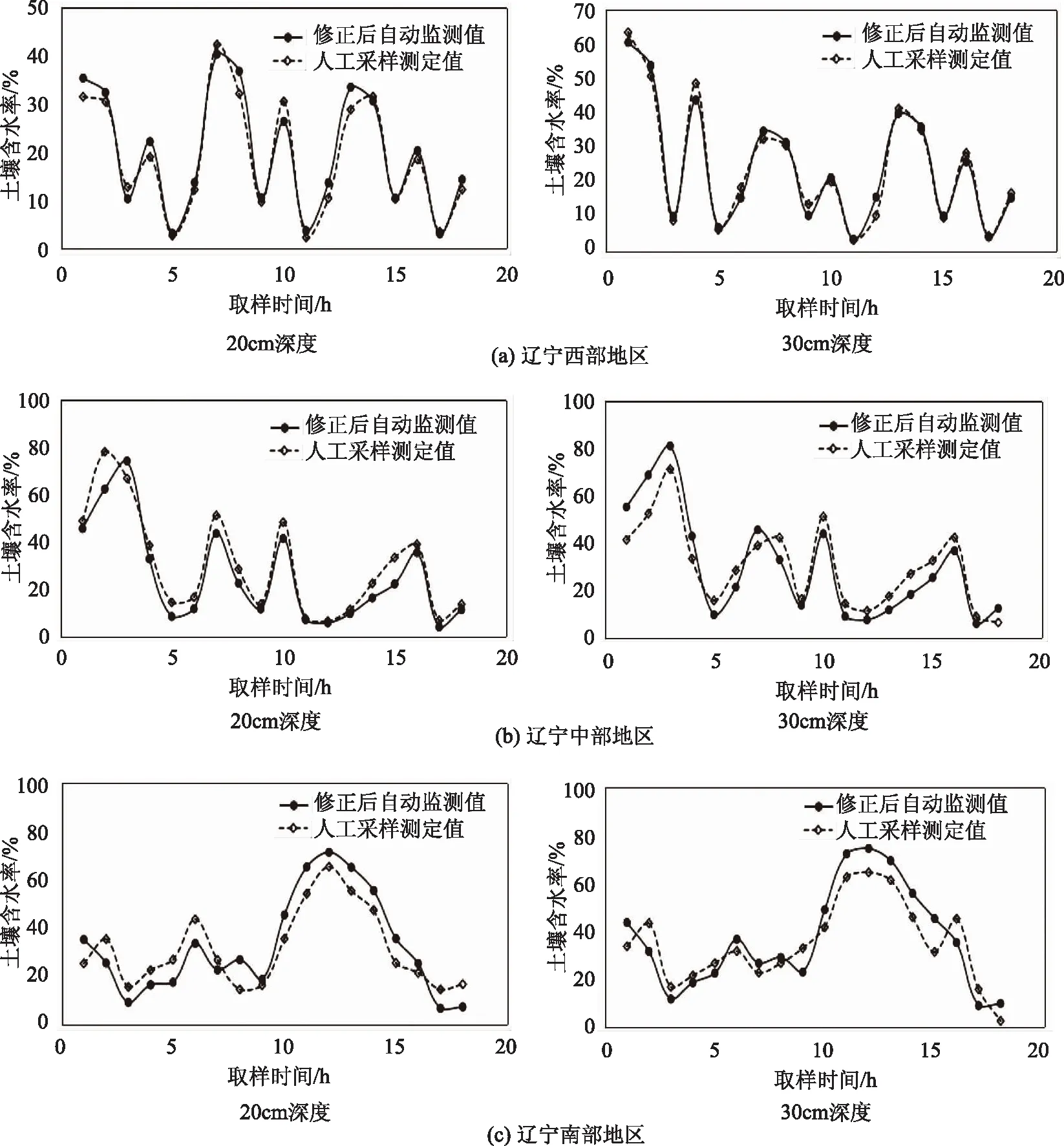
图2 各干旱分区自动土壤墒情监测数据误差修订曲线

表7为通过回归分析得到的各干旱分区不同土壤深度下的土壤自动墒情数据和人工观测数据之间的回归方程，为对各回归方程进行检验，绘制了各干旱分区的误差修订曲线。从图2中可以看出，采用回归方程对自动墒情监测数据进行修正后，各深度下自动墒情数据和人工测定数据之间的吻合度均较好。通过前面的误差分析可以看出，自动墒情误差较大的原因主要为各时间段测定误差及仪器的频数设置的误差，通过建立回归方程，可以对土壤墒情数据进行误差部分消除，提高自动墒情测定的精度，且结合各分区不同深度下的误差修订曲线，可以对区域内其他墒情站点进行误差消除，提高其自动墒情监测精度，从精度评定结果可看出，相比于修正前，采用误差修订曲线进行修正后，土壤自动墒情站点监测精度提高15%～30%，基本可满足墒情监测的精度要求。

2.5 误差修正方程对比

结合不同回归方程对各自动墒情类型下的误差精度进行分析，分析结果见表8—10。其中，BZC为标准差，MAX为最大误差，MIN为最小误差，JDWC为绝对误差。

从不同回归方程的误差统计结果均可看出，随着回归次数的增加，不同类别的误差均有所减小，这主要是因为回归次数的增加，使得各类误差得到一定程度的均化，但是回归次数的不断增加，也不能完全提高自动墒情的误差测定精度。从分析结果可看出，对于辽宁省各干旱分区而言，采用一元三次回归方程进行误差修正后，其精度可得到有效提高，可满足旱情监测的精度规范需求。因此建议在各干旱分区，随着自动墒情监测站点数据系列的不断增加，逐步采用一元三次回归方程进行土壤墒情监测数据的修正，提高各区域墒情监测的精度。