厘清概念夯实基础

戴倍琪

平行四边形是同学们初中阶段接触的特殊四边形，在边、角、对角线、对称性方面呈现出特有的性质与特征。要学好相关内容，就必须对平行四边形的定义、性质、判定及应用有较好的理解与掌握。下面通过一道中考题，帮助同学们加深对相关知识的理解，并能熟练应用。

例 （2013·江苏无锡）如图1，四边形ABCD中，对角线AC与BD相交于点O，在①AB∥CD，②AO=CO，③AD=BC中任意选取两个作为条件，以“四边形ABCD是平行四边形”为结论构造命题。

（1）以①②作为条件构成的命题是真命题吗？若是，请证明;若不是，请举出反例。

（2）写出按题意构成的所有命题中的假命题，并举出反例加以说明。（命题请写成“如果……，那么……”的形式）

【分析】第（1）问，由①AB∥CD的条件可得出∠OAB=∠OCD的结论，加上②AO=CO的条件，以及∠AOB=∠COD，可以证明△AOB≌△COD，得BO=OD，得到四边形ABCD对角线AC、BD互相平分，从而证明四边形ABCD是平行四边形。

第（2）问，应列举所有的可能性①②、①③、②③，并加以甄别。由第一小题的证明可得出①②是真命题。接下来分析①③，一组对边平行，另一组对边相等，同学们能够举出等腰梯形的反例，难度不大。再看②③，数学基础不够扎实的同学非常容易出错。在△AOD和△COB中，AO=CO，AD=BC，∠AOD=∠BOC，这正是全等三角形中的典型的错误证明——SSA。如若不能厘清概念，对全等判定条件没有深刻的理解，那么对于中考中类似的题目，很可能就搞不清楚了。

（2）以①③作為条件构成的命题是假命题，即如果一个四边形有一组对边平行，另一组对边相等，那么这个四边形是平行四边形。如图2，四边形ABCD中，AB∥CD，AD=BC，但四边形ABCD不是平行四边形。其实，这时的四边形ABCD是等腰梯形。

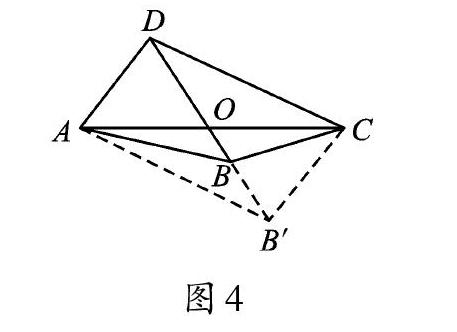
以②③作为条件构成的命题是假命题，即如果四边形ABCD的对角线AC、BD交于点O，AO=CO，AD=BC，那么这个四边形是平行四边形 。如图3，AO=CO，AD=BC，但四边形ABCD不是平行四边形。其实，这里就涉及全等三角形判定中对“SSA”的理解问题。在△AOD与△COB中，满足“两边相等、一角相等”，但这两个三角形并不全等，原因就是其中的角不是两边的“夹角”。所以“SSA”与“SAS”的内涵是不一样的。满足AO=CO，AD=BC（或AD=B′C）的三角形有两个，即△COB和△COB′，如图4。

在综合运用时，同学们需要对各知识点融会贯通，比如平行四边形的判定方法，除了教材给出的判定外，“两组对角分别相等的四边形是平行四边形”“一组对边平行，一组对角相等的四边形是平行四边形”都是真命题。同学们要善于通过转化的数学思想来解决实际问题。

（作者单位：江苏省无锡市雪浪中学）