图形旋转之妙用

马娇 孙晓峰

同学们，大千世界，运动变化可以说无处不在，运动与我们紧密相连。在数学世界里图形的运动为我们解决问题带来很多便捷，也增添了不少乐趣。利用平移、翻折、旋转，我们的答题能更加简单。

下面让我们一起走进图形的旋转，领略其巧妙之处。

例1 如图1，已知正方形ABCD，E、F分别是CD、BC上的点，且∠EAF=45°，则线段BF、DE、EF之间的关系式是__________。

【解析】基于對全等知识的研究和运用，一部分同学会立马想到在△AEF中构造与△ADE或△ABF全等的△AEH或△AFH（如图2），但发现不管是在EF上作EH=ED，还是作∠DAE=∠HAE，或是作AH⊥EF，要证明三角形全等，都只具有两个条件，因此利用分割证全等得不出答案。

我们再来回顾一下题目条件，看看能否得出什么信息。不难发现AB=AD，∠DAB=90°=2∠EAF=∠D=∠ABC，得到∠DAE+∠BAF =∠EAF=45°。我们要解决BF、DE、EF三者间的关系，可以将短线段合理变换，把BF放到直线DC上，再证明全等，于是旋转自然就巧妙构建出来了。将△ABF绕点A逆时针旋转90°得到△ADG，如图3，证明△AEF与△AEG全等，即可说明BF、DE、EF三者关系为EF=BF+DE。需要提醒的是：由旋转形成的图形，在进行推理说明时，一定要说明E、D、G三点在一条直线上。为避免证明三点共线，我们可以延长ED到G，使GD=BF，然后两次证明全等即可。同学们阅读完后，不妨自己动手写写看。

例2 如图4，在四边形ABCD中，∠BAD=∠C=90°，AB=AD， AE⊥BC于E，若线段AE=5，则S四边形ABCD=                   。

【解析】受前例启发的同学，估计很快想到捷径——巧妙构建旋转（如图5），把△ABE绕点A逆时针旋转90°，得到正方形AECF，则四边形ABCD的面积即为正方形AECF的面积，结果为AE2=25。利用旋转将不规则四边形转化成特殊四边形，利用特殊四边形面积公式进行计算，简单直观。

讲到这里，不知大家有没有产生疑惑，为什么以上两题都可以用旋转？两个问题有什么共性的本质可以遵循呢？

感悟：旋转的本质——旋转前后的图形是全等形，旋转前后的对应线段、对应角相等。例1、例2的共同特征是在一个顶点处有两条相等线段，条件里四边形的相对内角和为180°，即等线段、等角。

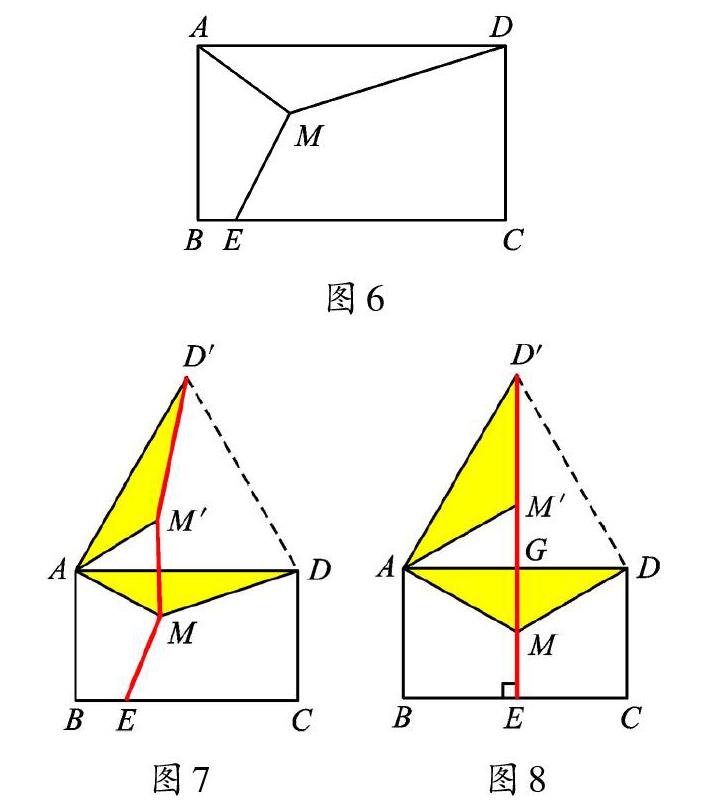
例3 如图6，已知矩形ABCD，AB=4，BC=6，点M为矩形内一点，点E为BC边上任意一点，则MA+MD+ME的最小值为                      。

【解析】刚读完题后，从题目条件观察思考是不是找不到解决的方法？我们再次读题，条件中得不到解题信息，那不妨从问题处着手突破。要求三线段和的最小值，联想到求两线段和的最值方法，只需要将现在的共点三线转化成三折线，而且三折线在两个顶点之间，因此应进行等线段转换。

感悟：本题特征是共点三线，利用旋转60°得到等边三角形，形成等线段，巧妙地转化成熟悉的模型。这就是旋转之奥秘。

阅读完三例，我们可以感受到数学中的无穷乐趣，旋转应用之巧妙。聪明的你，不妨动手试一下：

（作者单位：江苏省无锡市阳山中学）