无处不在的转化

宫乐 李岩

一、形到形的转化

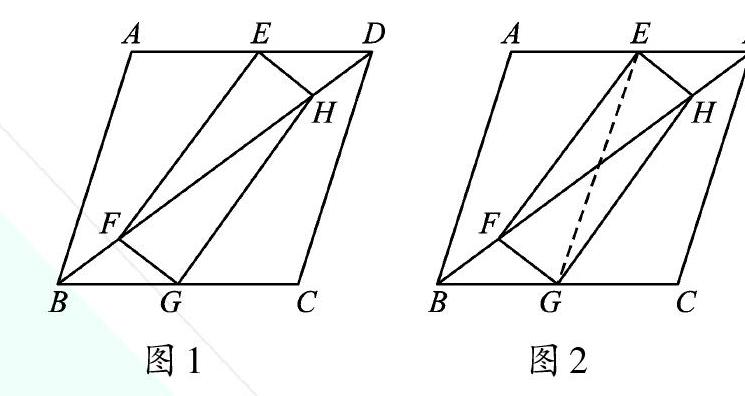
例1 （2019·浙江宁波）如图1，矩形EFGH的顶点E、G分别在菱形ABCD的边AD、BC上，顶点F、H在菱形ABCD的对角线BD上。

（1）求证：BG=DE;

（2）若E为AD中点，FH=2，求菱形ABCD的周长。

【分析】求证线段相等，最常用的方法是证明三角形全等，结合矩形、菱形的性质容易找到全等的三角形。（1）可以将四边形的问题转化为三角形的问题。（2）中要求菱形的周长，可先转化为求菱形的边长AB，结合条件FH已知，容易想到连接矩形EFGH的另一条对角线EG，通过证明四边形ABGE是平行四边形，将求菱形的边长转化为求矩形对角线的长。

解：（1）根据矩形的性质得到EH=FG，EH∥FG，得到∠GFH=∠EHF，求得∠BFG=∠DHE，根据菱形的性质得到AD∥BC，则∠GBF=∠EDH，可得△BGF≌△DEH（AAS），根据三角形全等的性质即可得到结论。

（2）如图2，连接EG，根据菱形的性质得到AD=BC，AD∥BC，结合（1）中的结论，证得AE=BG，AE∥BG，得到四边形ABGE是平行四边形，得到AB=EG，进而易得结论。

【点评】四边形的问题，经常是通过添加辅助线，将之转化为三角形的问题。例如，在新课的学习中，通过连接对角线，把平行四边形分割成两个全等的三角形，由全等三角形的性质得出平行四边形的性质。反之，在探究三角形的中位线时，是通过构造出平行四边形，利用平行四边形的性质得出三角形的中位线定理。把未知的图形转化为已知的图形，用已经掌握的知识来解决新问题，是分析、解决问題的基本策略。

二、形到数的转化

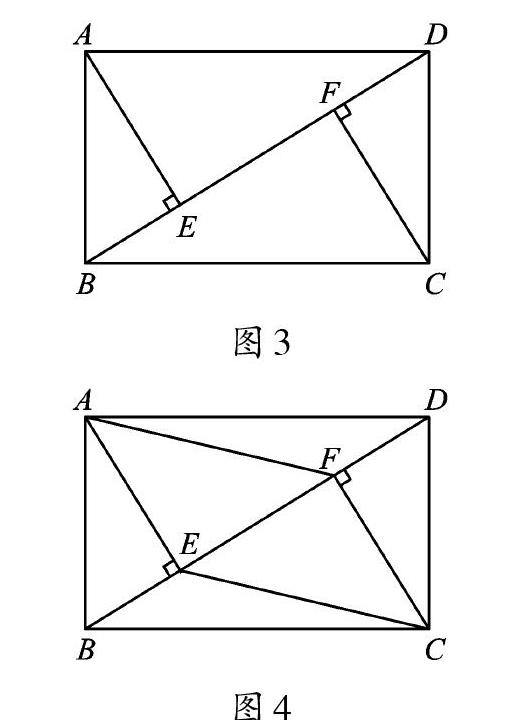
例2 （2019·黑龙江哈尔滨）已知：在矩形ABCD中，BD是对角线，AE⊥BD于点E，CF⊥BD于点F。

（1）如图3，求证：AE=CF;

（2）如图4，当∠ADB=30°时，连接AF、CE，在不添加任何辅助线的情况下，请直接写出图4中四个三角形，使写出的每个三角形的面积都等于矩形ABCD面积的[18]。

【分析】要找面积=[18]矩形面积的三角形，可根据矩形的性质、含30°角的直角三角形直角边和斜边特殊的数量关系以及三角形面积的计算方法，将三角形的面积转化为[18]×矩形长×矩形宽。

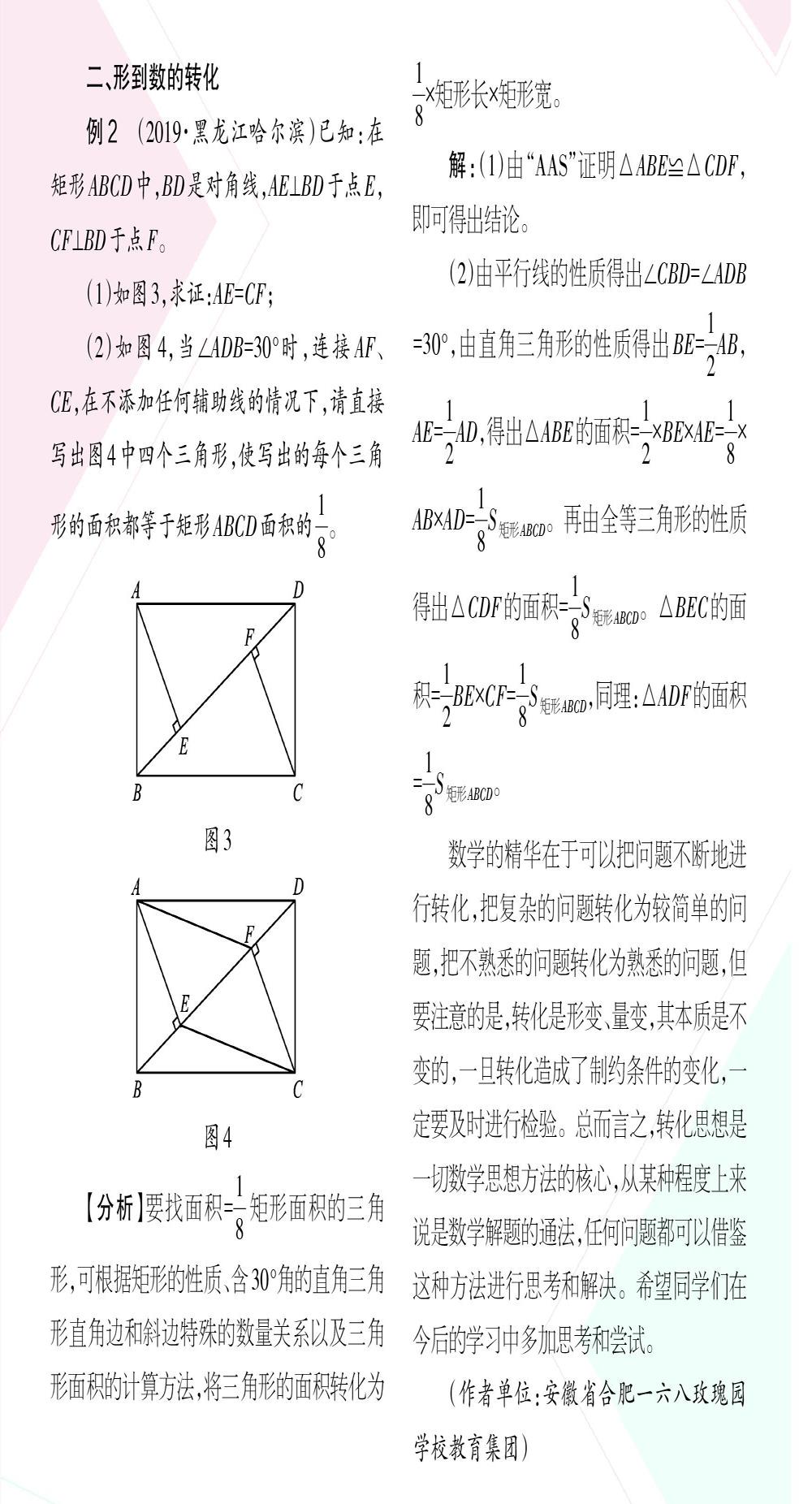
解：（1）由“AAS”证明△ABE≌△CDF，即可得出结论。

（2）由平行线的性质得出∠CBD=∠ADB=30°，由直角三角形的性质得出BE=[12]AB，AE=[12]AD，得出△ABE的面积=[12]×BE×AE=[18]×AB×AD=[18]S矩形ABCD。再由全等三角形的性质得出△CDF的面积=[18]S矩形ABCD。△BEC的面积=[12]BE×CF=[18]S矩形ABCD，同理：△ADF的面积=[18]S矩形ABCD。

数学的精华在于可以把问题不断地进行转化，把复杂的问题转化为较简单的问题，把不熟悉的问题转化为熟悉的问题，但要注意的是，转化是形变、量变，其本质是不变的，一旦转化造成了制约条件的变化，一定要及时进行检验。总而言之，转化思想是一切数学思想方法的核心，从某种程度上来说是数学解题的通法，任何问题都可以借鉴这种方法进行思考和解决。希望同学们在今后的学习中多加思考和尝试。

（作者单位：安徽省合肥一六八玫瑰园学校教育集团）