理清脉络学会思考

倪晓燕

一、利用多种手段，梳理知识脉络

在“中心对称图形——平行四边形”这一章中，许多同学解决四类特殊四边形的相关问题时，常常想法很多但又不知从何下手。其根本原因是同学们混淆了各类特殊四边形的概念、性质和判定，在解题时不知道如何选择。

本章知识点可以分解为三类。第一类是四类特殊四边形的性质。这部分知识可以用表格总结，从角、边、对角线三个方面进行归类，见表1，表示特有的性质。通过对比，同学们可以加深对特殊四边形性质的理解和记忆。

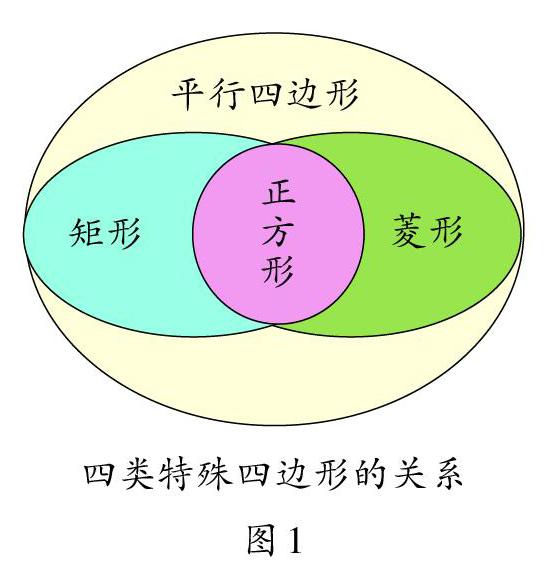
第二类是四类特殊四边形之间的关系。图1很好地表现了这种关系。矩形、正方形、菱形是特殊的平行四边形，它们有平行四边形所有的性质。正方形既有矩形的性质，又有菱形的性质。同学们正确理解四类特殊四边形之间的关系，可以帮助理解特殊四边形的性质和判定。

第三类是四类特殊四边形的判定。可以结合各特殊四边形之间的关系，做如下整理（见图2）。

二、确定解题“关键”，选择解題方法

1.分析已知条件，做出合情推理，寻找推理结论与目标结论之间的联系。

例1 如图3，O是菱形ABCD对角线的交点，DE∥AC，CE∥BD，连接OE。求证：OE=BC。

【分析】从“DE∥AC，CE∥BD”，可以根据平行四边形的判定1得出四边形DOCE是平行四边形;从“O是菱形ABCD对角线的交点”，可以根据菱形对角线的性质得出AC⊥BD。这两个结论结合，根据矩形的判定2得出四边形ODEC是矩形。以上是根据已知条件做出的推理。再分析目标结论“OE=BC”，OE是矩形ODEC的对角线，BC是菱形ABCD的边，因此可以由矩形对角线的性质得出OE=CD，由菱形边的性质得出BC=CD。由等量代换即可得到OE=BC。

2.分析目标结论，寻找需要条件，建立需要条件与已知条件之间的联系。

例2 判断：对角线相等的四边形是矩形。

【分析】由目标结论“矩形”确定应使用矩形的判定。联系已知条件中的“对角线”，选择“对角线相等的平行四边形是矩形”进行对比，原题缺少“平行四边形”，因此这一说法是错误的。

例3 判断：对角线互相垂直且平分的四边形是菱形。

【分析】由目标结论“菱形”确定应使用菱形的判定。联系已知条件中的“对角线”，选择“对角线互相垂直的平行四边形是菱形”进行对比，发现原题中有多余条件“对角线互相平分”“四边形”，缺少条件“平行四边形”。由平行四边形的判定4可知“对角线互相平分的四边形是平行四边形”，因此多余条件“对角线互相平分”“四边形”可以替换成条件“平行四边形”。因此这一说法是正确的。

“工欲善其事，必先利其器”，基础的性质定理就是解题的工具。因此，我们不能忽视对基础知识的梳理。同学们可以利用图形、表格等多种形式，寻找知识点间的关联，加深对基础知识点的理解和记忆。在思考问题时，既可以正向思考，从分析已知条件入手;也可以逆向思考，从分析目标结论反推。分析问题时，如果能找准关键词，就能准确地找到解题思路。

（作者单位：江苏省无锡市特殊教育学校）