基于三场变分原理的对偶mortar 有限元法

2020-06-01周墨臻张丙印张顶立方黄城

工程力学 2020年6期

周墨臻，张丙印，张顶立，方黄城

(1. 北京交通大学城市地下工程教育部重点实验室，北京 100044；2. 清华大学水沙科学与水利水电工程国家重点实验室，北京 100084)

对计算域剖分整体协调网格是传统有限元方法对前处理建模的基本要求。然而，对复杂工程问题的大规模计算，这一要求可能成为巨大挑战[1]。在工程应用中，使用非协调网格的需求十分普遍，例如，疏密网格过渡或自适应网格加密[2―4]、多尺度模拟[5―6]、非线性接触[7―9]、基于区域分解的并行计算[10―11]、边界元或有限体积法等与有限元的耦合[12―14]、多物理场耦合[15―16]等。目前，面向有限元的非协调网格处理技术主要有点-面法[7,17]、面-面法[14,16,18―19]、Nistche 法[20]、特殊界面连接单元[3,6,10,21]、三场变分法[2,22―23]、四场变分法[13,15]、多面体单元[24―25]、比例边界有限元[26]、局部无网格法[1,5]等。

在这些方法中，mortar 元[18―19]作为最具代表性的一种面-面方法，由于求解精度高且具有较好灵活性而得到广泛应用，并成功嵌入 ABAQUS 和ANSYS 等商业软件[27―29]。然而，随着工程应用对有限元计算在复杂化和精细化等方面的要求不断提高，mortar 元表现出了以下不足：

1) 约束交叉问题。如图1 所示，当两个以上子区域的界面在同一处发生重叠，二维问题会出现交叉点，三维问题则出现交叉线，从而导致界面约束条件之间发生交叉，需进行特殊处理。

图1 交叉点或交叉线问题 Fig.1 Cross-point or cross-line problems

2) 主从偏见问题。Mortar 元将非协调网格两侧的界面分为主面和从面，其主要目的是将从面用于离散Lagrange 乘子(以下均简称为乘子)。这种主从关系是由数值算法所引入的非物理概念，需要人为指定，且主要依赖于计算经验。尤其对图1 所示的约束交叉情形，主从关系的选择更为困难。

3) 求解效率问题。Mortar 元一般采用罚函数法、乘子法或增广Lagrange 法施加界面约束，可引起矩阵病态、矩阵非正定或额外迭代层等问题。这些问题在中小规模计算时并不突出，但对大规模计算则会严重影响整体求解效率。

上述问题虽然均可在计算力学领域内找到各自的解决途径，但若要同时解决，且还保留mortar元的固有优势，则仍需深入研究。例如，Nistche法[20]可解决问题1)和2)，但通常需要增加稳定项以避免矩阵病态，而对非线性材料，还需推导本构关系的变分，处理困难；再如，使用分片常量函数插值乘子[14,30]可解决问题1)和3)，但代价是乘子不连续，精度较低；此外，采用对偶基函数插值乘子，也就是对偶mortar 元[16,31]，可解决问题3)。由于该特点，对偶mortar 元得到了较快发展，也是目前等几何分析中的热点问题之一[32―38]。但对偶mortar元对问题1)也需要特殊处理，一般是在约束交叉处缩减乘子[32―39]，但这一处理需检测约束交叉面片，复杂工程应用存在不便。

本文基于mortar 元的理论框架，采用三场变分原理，提出了引入媒介面的对偶mortar 有限元法。该方法可同时解决约束交叉、主从偏见和求解效率问题，无需缩减乘子，对材料非线性问题也不引入额外困难，为非协调网格处理提供了一种新途径。

1 三场变分法

1.1 数学描述

图2 以三个子区域Ωα为例(上标α用以代表不同的子区域)，示意了本文所涉及的各类边界条件。Dirichlet 和Neumann 边界分别记为和。假定在每个Ωα内各自剖分协调网格，而不同子区域之间的网格相互独立，由此导致的网格非协调表面记为Γα，并简称为实体面。

图2 子区域界面及媒介面示意 Fig.2 Schematic of subdomain interfaces and the medium face frame

区别于mortar 元，本文引入一个虚拟的媒介面Γm，其网格剖分完全独立于各个子区域的实体网格。由于各子区域之间以及子区域与媒介面之间均不满足有限元计算的连续性要求，因此，需要构造连续性条件。为叙述简便，以下均以基于位移求解的应力变形有限元计算为例。

将实体区域和媒介面内任意物质点的位形分别记为Xa和Xm(如图2 示)，位移分别记为αu和um。界面间的位移连续性条件可描述为：

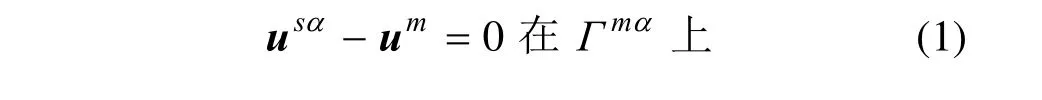
式中：usα为实体面Γα上的位移。Γ mα为实体面和媒介面之间经过投影之后所产生的重叠区域，具体投影方法将在2.2 节详细介绍。

在mortar 元中，界面连续性条件定义为从面与主面之间的相对位移为零，显然从面和主面均对应于本文的实体面，因而导致主从偏见问题。本文的连续性条件定义为实体面和媒介面之间的相对位移为零，不同的实体面之间无需定义连续性条件，从而可直接解决约束交叉和主从偏见问题。

1.2 弱形式

采用Lagrange 乘子法施加式(1)所示的耦合约束条件，则约束变分原理给出：

式中：δΠ为泛函变分；为各个子区域的虚功，由常规有限元理论确定，此处略去其具体表达；和分别为界面虚功和界面连续性条件；αλ表示乘子，物理含义是界面力。可见，上述变分原理共涉及三个待求解的未知场变量：αu、um和αλ。因此，式(2)也称为三场变分法[22―23]。

若将位移进一步分解为刚体位移和变形，则三场变分法将演变为四场变分法[15]。四场变分法的主要特点是利用刚体平衡等条件，布置媒介面的网格结点。本文采用的三场变分法只需满足式(2c)所示的连续性条件，而无需其他额外方程，且媒介面的网格剖分完全独立于实体区域。

mortar 元由于不涉及媒介面的位移场mu，因此，对应二场变分原理。本文以下将mortar 元的理论框架由二场变分原理扩展到用于三场变分原理，并通过采用对偶mortar 元解决求解效率方面的问题。

2 三场对偶mortar 元

2.1 空间离散

各子区域的位移αu采用线性实体等参单元，媒介面的位移um采用线性表面等参单元：

式中：Nα和Nm分别为子区域和媒介面的单元形函数矩阵；dα和dm为相应的离散位移。

乘子λα离散在实体面Γα上：

式中：zα表示离散后的乘子；ψα为乘子的插值函数矩阵。mortar 元一般直接取ψα=Nα，而在对偶mortar 元中，ψ α则采用满足如下双正交特性的对偶基函数[28]：

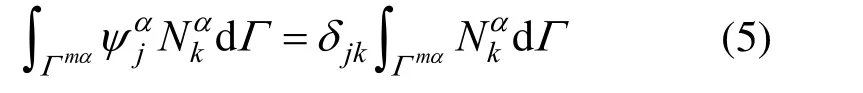
式中，δjk为Kronecker 函数。为确定ψα，可将积分域Γ m,α分解到每个实体面的表面单元上：

式中，e mα表示媒介面经投影后与实体表面单元之间的重叠区域，其计算方法将在2.2 节具体介绍。

假定ψα为Nα的线性组合：

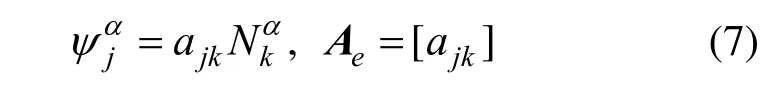
式中：jka为待定系数；Ae为系数矩阵。将式(7)代入式(6)可得：

由式(8)可求解得到待定系数jka，从而确定对偶基函数αψ的具体形式。值得指出的是，上式中矩阵eM的大小仅取决于单个表面单元的结点个数，因而其求逆计算的代价很小。

将式(3)和式(4)分别代入式(2b)和式(2c)，可分别得到界面虚功和连续性条件的离散形式：

式中，dsα表示usα的空间离散形式。矩阵Dα和Mα分别为：

式中，3I表示3×3 的单位矩阵，因为三维问题中位移共有3 个自由度。由式(10a)可见，矩阵αD为严格对角矩阵，这是由式(5)所确定的。这一特性对提高求解效率具有关键作用，2.4 节将具体介绍。

2.2 界面投影及数值积分

在早期mortar 元中，界面积分域e mα直接取为整个从面单元。研究表明，该种做法可能导致较大数值误差。本文将mortar 元的投影与积分改进研究[18]推广用于三场对偶mortar 元。主要步骤如下：

1) 如图3(a)示，将实体表面单元eα和媒介面单元em均按eα中心点处的法向进行投影，从而将三维面单元降维成二维平面单元。

2) 如图3(b)示，对两个平面单元使用多边形裁剪算法，得到二者之间的多边形重叠区域e mα。

3) 如图3(c)示，对e mα进一步作三角剖分。图3(c)示意了剖分得到的7 个三角形子片段et。

4) 如图3(d)示，将相关的积分项在三角形子片段et上作积分，本文采用7 点Hammer 积分。

图3 投影方法和积分方案 Fig.3 Projection method and numerical integration

由此，式(8b)～式(8c)和式(10a)～式(10b)可分别计算如下：

式中：Hi为第i个积分点的积分权系数；表示Jacobian 行列式。需注意的是，上式中的插值函数、、和定义在eα或me上，而积分点则定义在三角形子片段上。因此，需要根据积分点的笛卡尔坐标，在eα和me上作等参逆变换，在得到等参坐标之后，再计算插值函数。

2.3 线性方程组

由式(2)和式(9)，可写出总体线性方程组如下：

式中：上标s为实体面Γα上的自由度子集；上标R则表示实体区域中除实体面Γα之外的自由度子集。K、Fext、ds、dR、D、M和z表示由各子区域Ωα的相应子块所构成的矩阵或列向量：

式中：n为子区域的数目；Kα和分别为第α个子区域的总体刚度矩阵和外力，由确定，属于有限元的常规计算内容，此处略去具体表达。D α和Mα由式(11c)～式(11d)计算后集成得到。

2.4 乘子凝聚

在式(12)中，矩阵第3、4 行的对角元素均为零，使得矩阵失去正定性，导致鞍点问题。其次，乘子自由度z为待求解的未知量，增加了矩阵规模。为此，基于通用矩阵变换[40]，对乘子进行凝聚：

式中，ds表示实体面与媒介面的相对位移，可通过矩阵C表示如下：

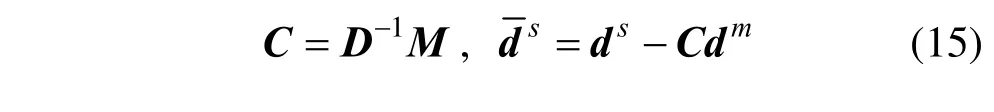
将式(15)代入式(12)的第4 行可得：

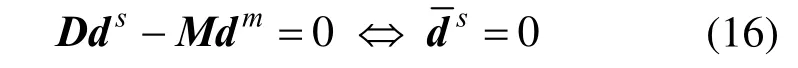
式(16)将耦合约束变换成为完全解耦形式。也即，对式(14)而言，式(16)等价为Dirichlet 边界条件，可采用直接消去法施加。这表明：虽然媒介面引入了额外自由度，但实体面的自由度可全部消去，矩阵规模可基本不受影响。同时，经过变换之后，式(14)不再包含乘子自由度z，且矩阵恢复了正定性。至此，只需求解满足式(16)的式(14)，而无需再求解式(12)，从而解决了求解效率方面的问题。

需要指出的是，若使用常规mortar 元，则矩阵D不是对角阵，而式(15)需求解1-D，计算代价很高。三场对偶mortar 元由于使用式(5)所示的双正交条件，使得D为严格对角矩阵，其求逆代价可忽略不计，式(15)可很方便地计算得到。

3 数值算例

基于所提出的三场对偶mortar 有限元，采用C++语言自主编制了相应的三维计算程序。以下采用两个数值算例，对该计算程序进行验证。两个算例均采用杨氏模量E= 1×105Pa、泊松比ν= 0 的线弹性材料。此处，选取泊松比ν= 0 的主要目的是简化理论解，虽与实际工程计算存在差别，但属于检验非协调网格处理效果的一般做法[26,41]。

3.1 接触分片试验

接触分片试验常用于检验接触数值算法处理非协调网格的能力，一般仅考虑两个子区域。为检验处理约束交叉问题的能力，此处将2 m×2 m× 2 m 的计算区域考虑为5 个子区域。实体网格如图4(a)所示，其中，1Ω～4Ω剖分各向等长的六面体单元，单元长度分别为1/4 m、1/5 m、1/6 m 和1/7 m，Ω5的单元尺寸为2/7 m×2/7 m×1/3 m。媒介面网格如图4(b)所示，单元为各向等长，长度为1/3 m。

图4 接触分片试验计算网格 Fig.4 Computational mesh of the contact patch test

对图4(b)所示的约束交叉线，mortar 元需检测相应面片并缩减乘子，本文方法则无需任何特殊处理，也无需检测。同时，计算时完全无需对Ω1～Ω5的实体面区分主从关系，很好地避免了mortar 元的主从偏见问题。计算的边界条件为：Ω1～Ω4的上表面施加大小为1 Pa 的法向均布压力，Ω5的下表面所有结点均取为固支约束。显然，该问题的理论解是单向应力状态，且各处竖向应力均为-1 Pa。

计算结果如图5 所示。在图5(a)中，黑色线条表示位移等值线。可见，计算所得最大竖向位移为-2×10-5m，与理论解吻合，且图中未见明显位移不连续现象。在图5(b)中，黑色线条表示网格线。可见，计算所得竖向应力为均匀分布，图示的数值在-1±10-6Pa 之间。为反映计算准确性，定义位移、应力及能量的相对误差如下：

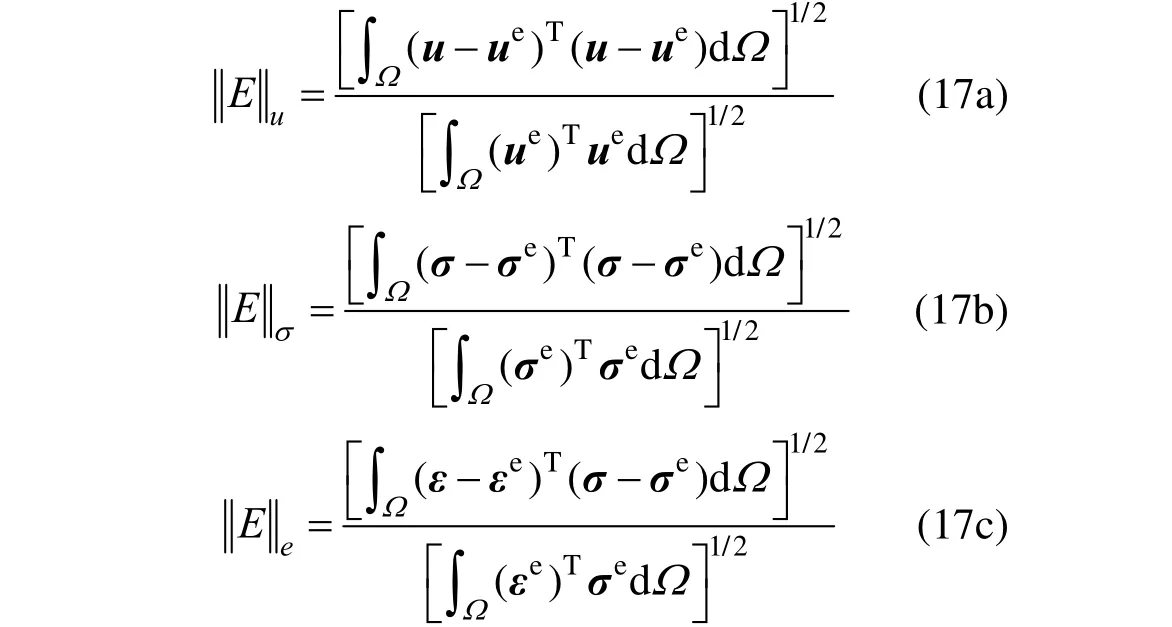
式中，ue、σe和εe分别为位移、应力及应变的理论解。

图5 接触分片试验的数值计算结果 Fig.5 Numerical results of the contact patch test

统计得到的位移、应力及能量误差分别为1.83× 10-8、4.17×10-8和4.63×10-8。考虑到机器精度，可认为计算结果与理论值吻合。若直接使用二场mortar 元，而不在交叉点处缩减乘子，则上述误差分别为1.06×10-4、1.34×10-3和1.44×10-3。可见，本文所提出的三场对偶mortar 元无需处理交叉点，也可对约束交叉问题具有很高的求解精度。

为检验求解效率，采用预处理共轭梯度法PCG(preconditioned conjugate gradients)求解线性方程组，分别对三场对偶mortar 元和罚函数法进行测试。表1 统计了PCG 方法在使用不同预处理时的迭代次数。可见，在三种预处理情况下，三场对偶mortar 元的迭代次数均远少于罚函数法，验证了该方法在求解效率方面的优势。

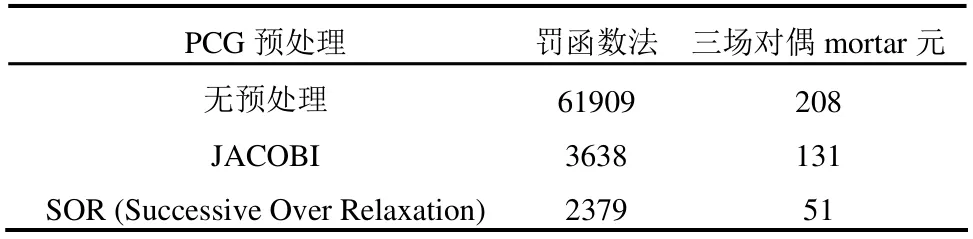
表1 线性方程组求解迭代次数 Table 1 Iterations of solving the linear system

需指出的是，对Lagrange 乘子法所导致的鞍点问题，PCG 方法无法求解，需使用稳定双共轭梯度法 BICG-STAB(Bi-conjugate gradients stabilized method)等特殊方法，且求解效率较低。而增广Lagrange 法则由于引入额外迭代层，即便对线性问题也可能需要多次求解线性方程组，整体效率受较大影响。对这两种情况，本文不再一一验算。

3.2 带圆孔平板

为进一步验证对约束交叉问题的处理能力，考虑如图6(a)所示的弹性力学经典平面应力问题：带圆孔无限平板的单向均匀拉伸。该问题的位移及应力解析解可参见文献[20]。

鉴于对称性，可取图6(a)的1/4 进行计算。而对无限域，则截取圆孔周围一定范围内的平板进行分析，如图6(b)所示。为使得应力变形状态与图6(a)一致，对图6(b)所示模型，施加x向和y向对称约束，并根据应力的解析解，计算左侧及上部边界的面力，将其作为面力边界施加在相应表面[20]。

根据图6(b)所示意的10 个子区域，剖分了如图7 所示的疏密相间三维计算网格，以检验数值算法处理复杂子区域划分的能力。计算区域平面尺寸为4 m×4 m，厚度为1 m，无限远处的拉力p= 1 Pa，圆孔半径取为1 m。在图6(b)和图7(a)中，分别对笛卡尔坐标系和柱坐标系进行了示意。

图6 带圆孔无限大平板示意 Fig.6 Schematic of the infinite plate with circular hole

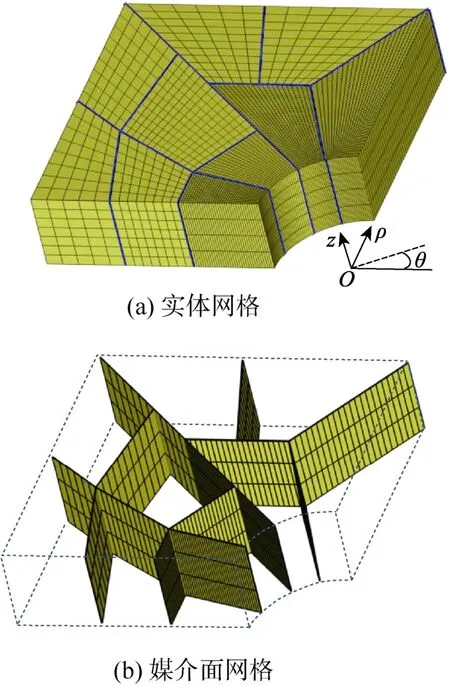
图7 带圆孔平板计算网格 Fig.7 Computational mesh of the plate with circular hole

计算结果如图8 所示。在图8(a)～图8(b)中，黑色线条表示位移等值线。可见，计算所得x向和y向位移分布规律与理论解一致，且未出现明显位移不连续现象。在图8(c)中，黑色线条表示网格线。可见，计算所得应力σxx在圆孔顶部出现明显应力集中现象，最大应力值为2.987 Pa，与解析解所给出的3 Pa 十分接近。为进一步对比分析，本文另补充了针对图9 所示协调网格的计算。

图10 给出了计算所得应力σxx沿圆孔的分布及其与解析解的对比情况，柱坐标θ的定义如图7(a)所示。由图可见，非协调网格得到了与协调网格几乎一致的计算结果，且均与解析解十分接近，验证了三场对偶mortar 元处理非协调网格的有效性。

图8 带圆孔平板的数值计算结果 Fig.8 Numerical results of the plate with circular hole

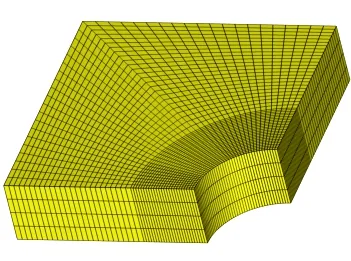
图9 带圆孔平板的协调有限元网格 Fig.9 Conforming mesh of the plate with circular hole

图10 数值计算结果与解析解的比较 Fig.10 Comparison of the numerical and analytical results

4 关于媒介面网格的讨论

在上述的两个算例中，媒介面的网格均具有两个特点：1) 自身协调；2) 密度低于实体网格。

在实际工程应用中，满足第一个特点并不会引入很大困难。这是因为媒介面相比于实体区域而言，只需剖分降维后的网格。相当于以剖分一个协调的面网格的代价，实现了不同子区域的网格各自独立剖分，且子区域的划分形式不限。

第二个特点，更准确地说，是要求媒介面的网格不能比实体网格中较密的那一侧更密。若不满足这一要求，则会导致式(14)中第三行存在线性相关性，也即矩阵病态。实际应用通常可方便地满足这一要求，更多讨论细节可参见文献[22]。考虑到工程问题的复杂性，允许媒介面网格任意剖分而无需格外顾及网格密度的限制，同样具有研究意义。关于该问题的解决，限于篇幅将另文讨论。