改进小波阈值函数在变形监测数据去噪中的应用

甘 若,陈天伟,郑旭东,段青达,潘 梅

(桂林理工大学 a.广西空间信息与测绘重点实验室;b.测绘地理信息学院,广西 桂林 541006)

在变形监测数据中,噪声经常影响分析结果的准确性。由于人为操作和测量仪器精度等因素,对建筑物进行监测得到的变形数据含有真值和误差(噪声)两部分,如何有效消除误差并提取变形特征、最大限度地还原真实信号，是变形分析研究的重要内容。国内外学者对变形监测数据处理及预测方法进行大量的研究和总结,归纳出大量理论和方法,如小波分析、神经网络、线性回归法、灰色预测模型、卡尔曼滤波等,这些方法都已经成功运用于实际工作中,取得了不错的效果[1-4]。目前小波分析具有可平移、可伸缩、多分辨率、多尺度等多方面的优势,将小波分析应用到变形监测数据的处理中,可以更好地检测和削弱数据中各种误差的影响,这对于变形监测数据处理具有很重要的理论意义和实际应用价值。Donoho对小波去噪方法进行了研究,提出了小波软阈值和硬阈值去噪方法,获得了较好的效果[5],这两种阈值去噪方法获得成功的同时,也存在着不足之处，如硬阈值函数由于在阈值处的不连续性,会导致重构后的信号出现不必要的振荡现象。软阈值函数因为存在恒定的偏差问题,会导致重构后的信号丢失部分有效细节,出现失真的现象。针对传统阈值函数中出现的问题,学者提出了很多改进的阈值函数和解决方案[6-12],如:莫平方处理法、半软阈值处理法和软硬阈值折中算法等,其中赵瑞珍等提出的莫平方处理法能够有效提高信噪比,降低均方根误差[6];王知强提出的半软阈值去噪法有效地克服了硬阈值函数的不连续性,避免了软阈值函数存在的恒定偏差问题[7];王芳等提出的软硬阈值折中算法既兼顾了软、硬阈值函数的优点,同时又在一定程度上弥补了这两种方法的缺陷[8]。

针对传统阈值函数的缺点,结合研究现状,本文提出了一种改进的小波阈值去噪函数,探讨改进的小波阈值去噪函数对变形监测数据的去噪效果,验证改进阈值函数对变形监测数据去噪的有效性和可行性。

1 软阈值法和硬阈值法

小波传统的硬阈值函数和软阈值函数已经在实际工作中获得了广泛的应用,也取得了较好的应用效果,一些研究者在硬阈值函数和软阈值函数的基础上,提出了各种改进的阈值函数,其原理大多基于硬阈值函数和软阈值函数改进而成。

硬阈值函数为

(1)

式中:wj,k为硬阈值去噪后输出的小波系数;w为原始的小波系数;T为阈值(下同)。

软阈值函数为

(2)

此时，当|w|

2 小波改进阈值函数

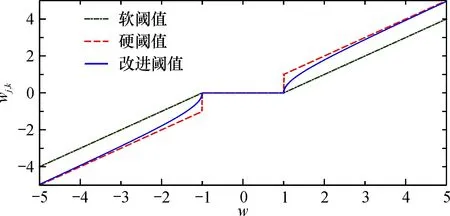
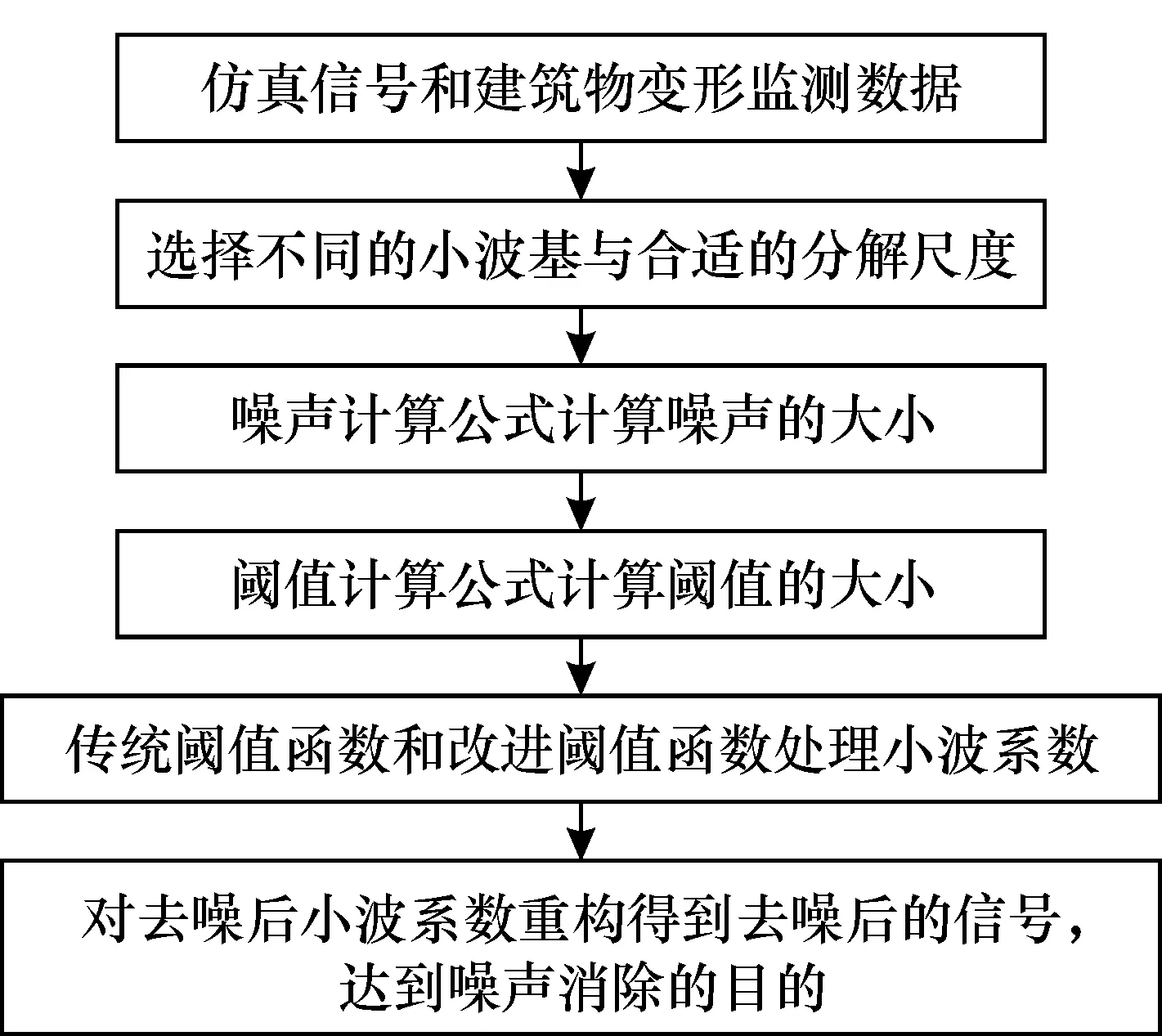
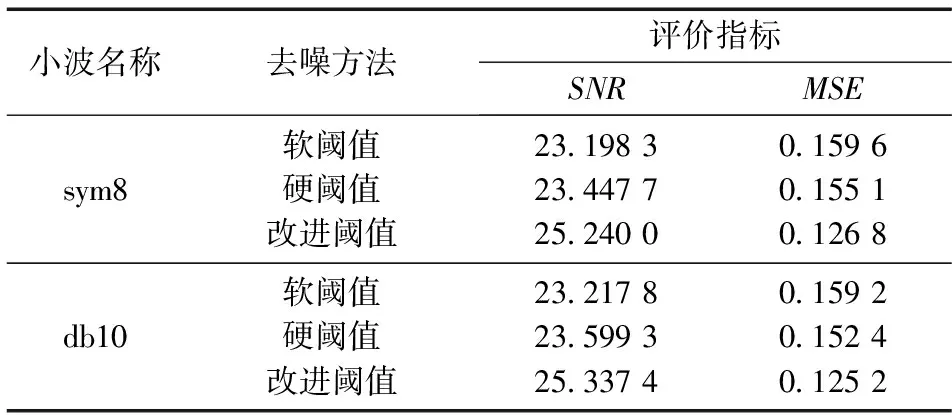
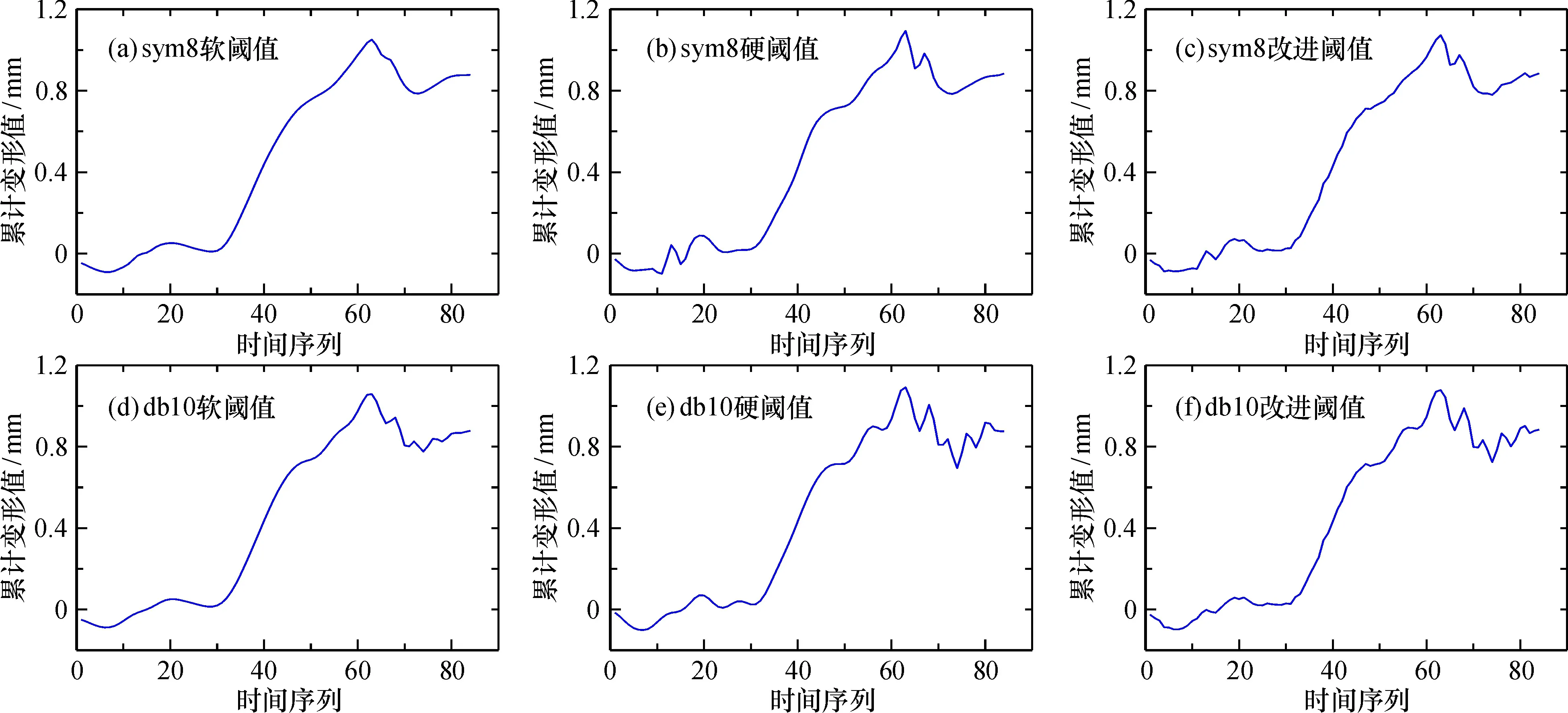
2.1 改进的阈值函数

针对软阈值函数和硬阈值函数的缺点,本文提出的改进阈值函数：

(3)

其中,M和β为可调节的参数,β∈(0.05,0.5),M>0。

改进的阈值函数具有以下特点: ①当w→±T时,e-(|w|-T)/M→1,wj,k→0,这表明改进的阈值函数具有和软阈值函数相同的特性,即在±T处连续;当w→∞时,e-(|w|-T)/M→0,wj,k→w,即wj,k=w是改进阈值函数的一条渐近线,这表明改进的阈值函数保留了硬阈值函数的特性,估计值更加接近于实际值。 ② 参数M用于实现不同的M值对改进阈值函数去噪效果的影响,图1为改进阈值函数不同M值时的变化曲线。 当M→0时,改进阈值函数接近于硬阈值函数,当M→∞时,改进阈值函数体现出软阈值函数的特征; 当|w|

图1 不同M值时的改进阈值函数Fig.1 Improved threshold function with different parameter M

从以上分析可以看出,改进的阈值函数不仅克服了硬阈值函数的不连续性,而且避免了软阈值函数连续不断的偏差现象。图2为当M=10时,改进阈值函数和软、硬阈值函数的变化曲线。

图2 M=10时软、硬阈值函数和改进阈值函数的变化曲线Fig.2 Soft,hard threshold function and improved threshold function with M=10

2.2 阈值估计方法

(4)

式中:σ为噪声强度;N为各层采样信号系数的长度;j为分解尺度。 阈值随着分解尺度变大而逐渐减小,对于阈值的选取,改进的阈值计算公式具有良好的自适应性,去噪的效果更好。

在实际过程中噪声的强度是未知的,不能直接利用噪声的标准差计算σ,因为用标准差直接计算σ,会影响去噪的精度,造成偏差。 在最小尺度空间,噪声的小波系数占据优势,因此可根据最小尺度空间的小波系数得出噪声强度[13]:

(5)

图3 去噪流程图Fig.3 Denoising flow chart

3 仿真试验

为了验证本文改进阈值函数去噪的有效性,使用MATLAB 2014a平台进行仿真试验。现模拟一组变形监测数据的仿真信号S,信号S由长度为500、3个振幅频率不同的周期项和1个趋势项组成,步长设置为0.01,仿真信号S的表达式为[14]

(6)

变形监测信号含有的噪声大多以白噪声为主,实验使用MATLAB中自带的awgn函数为仿真信号S添加信噪比为db15的高斯白噪声,仿真信号S和仿真噪声信号S1如图4所示。

本次实验采用传统阈值函数和本文的改进阈值函数进行对比分析,分别使用去噪能力较好的sym8小波和db10小波对含噪信号S1进行去噪处理。 当分解层数选为3层,改进阈值函数中M取值为2、β为0.15时,改进阈值函数的去噪效果较好,去噪效果如图5所示。 sym8和db10两种小波的软阈值去噪曲线太过平滑,失去了较多的有用信息,信号失真比较严重,这是由于软阈值函数把部分有用信号当成含噪信号去除的缘故。 sym8硬阈值去噪法基本去除了噪声,但在时间序列470～500处依然含有部分噪声,这是由于在对含噪信号S1进行信噪分离时,部分噪声信号分离到了低频信号当中,硬阈值去噪函数把噪声信号当成有用信号保留了下来,而且硬阈值函数在w=T处的不连续性,导致重构后的曲线产生了不必要的振荡现象。 db10硬阈值去噪曲线在时间序列150～200、270～300以及470～500处出现了部分振荡现象,去噪效果比sym8硬阈值去噪方法稍差。 改进阈值去噪曲线中,在时间序列470～500处sym8和db10两种小波都出现了振荡现象,其中sym8小波的振荡较明显,其余地方两种曲线差别不大,因此需要引进评价指标信噪比(SNR)和均方根误差(MSE)进行进一步的判断：

图4 仿真数据Fig.4 Simulation data

(7)

(8)

式中,fi为去噪后的信号;yi为原始信号;n为信号长度。SNR值越大,去噪效果越好；MSE值越小,去噪效果越好。

表1为各阈值函数去噪后的评价指标。sym8和db10软阈值去噪算法的信噪比较小,均方根误差较大,去噪的效果不太好,这是由于软阈值函数把部分有用信号当成噪声信号去除的结果,而且在|w|≥T时,wj,k与w存在固定的偏差T,对信号进行重构会产生较大的影响。 sym8和db10硬阈值去噪方法由于硬阈值函数在w=T处的不连续性,导致重构后的曲线出现了部分振荡现象,与软阈值去噪方法相比,信噪比和均方根误差相差不大,去噪效果较差。 sym8改进阈值去噪方法的信噪较大,均方根误差较小; db10改进阈值去噪方法的信噪最大,均方根误差最小。 改进阈值函数在一定程度上既避免了软阈值函数存在恒定偏差的问题,又克服了硬阈值函数的不连续性,去噪效果比传统阈值法有了进一步的提高,可见本文的改进阈值函数对模拟的变形监测数据去噪是可行的。

图5 各阈值函数用不同去噪方法对变形值的去噪效果Fig.5 Denoising effect of threshold functions on deformation values with different denoising method

表1 各阈值函数去噪后的评价指标Table 1 Quality evaluation after denoising of each threshold function

4 实例分析

由于仿真信号添加的噪声较为单一,而变形监测信号所含有的噪声较为复杂且无规律,现通过工程实例进一步验证本文阈值函数的去噪能力。数据来源于文献[15]某市地铁施工建筑物变形监测,其中以Q-18点的倾斜观测数据作为原始信号,如图6所示。

可见,该建筑物的变形监测数据含有一定的噪声,数据波动较大,带有较多毛刺,具有一定周期性,建筑物总体呈现出逐渐向下倾斜的趋势。

为考察去噪效果,采用传统阈值函数和本文改进阈值函数进行对比分析,分别使用sym8小波和db10小波对含噪信号S1进行去噪处理。 分解层数选为3层,改进阈值函数中M为2、β取0.15时,改进阈值函数的去噪效果较好,去噪效果如图7所示。

图6 建筑物Q-18点原始信号Fig.6 Original signal of building Q-18 point

可以看出,sym8软阈值去噪曲线总体上过于平滑,失真比较严重,周期性变化不明显,不能有效地提取变形信息,过度平滑了原始变形监测数据,这是因为含噪的小波系数和估计的小波系数之间存在恒定的偏差T,重构以后的精度比较差,导致去噪后的曲线过于光滑。db10软阈值去噪曲线在时间序列0～60处的细节不明显,失真也比较严重,而且在时间序列60～84处的振荡比较明显,还存在部分噪声。 sym8硬阈值去噪曲线由于在w=T处的不连续性,导致重构后的曲线出现了部分振荡现象,特别是在时间序列10～20和60～70处的振荡较为严重,去噪效果较差。 db10硬阈值去噪曲线在时间序列60～84处的振荡现象比较严重,还含有部分毛刺,去噪效果较差。 sym8和db10改进阈值去噪方法与传统阈值去噪方法对比,在时间序列10～30处的细节比较明显。 db10改进阈值去噪曲线在时间序列60～84处的振荡比较明显,还有较多毛刺,从曲线上看,去噪效果比sym8改进阈值曲线去噪曲线稍差。其余地方两种小波的改进阈值去噪曲线差别不大,需要从评价指标上进一步判断本文改进阈值函数去噪的有效性和可行性,表2为各阈值函数去噪后的评价指标。

图7 各阈值函数用不同去噪方法对累计变形值的去噪效果Fig.7 Denoising effect of threshold function on cumulative deformation values with different denoising method

表2 各阈值函数去噪后的质量评价Table 2 Quality evaluation after denoising of each threshold function

可以看出,sym8和db10两种小波的软阈值去噪方法的信噪比较低,均方根误差较大,去噪的效果不是很好,这是由于软阈值函数存在恒定偏差的问题,导致重构后的信号出现失真现象,精度降低。 sym8和db10两种小波的硬阈值去噪方法由于不连续性会导致重构后的曲线出现振荡现象,与软阈值去噪方法对比,信噪比有提升,均方根误差有下降,去噪效果不是很明显。sym8改进阈值去噪方法的信噪比较大,均方根误差较小； db10改进阈值去噪方法的信噪比最大,均方根误差最小,与传统阈值去噪方法相比,去噪效果有较明显的提升。 对于含有较多毛刺、噪声密集,且数据波动较大的变形监测信号,本文改进阈值函数对变形监测数据的去噪效果较为理想,能够保留信号更多的有效细节。

5 结 论

通过构建改进的小波阈值去噪函数,对模拟的变形监测数据和真实的变形监测数据进行了去噪处理,结合图像分析和评价指标,结果表明: 改进阈值函数的去噪效果比传统小波阈值效果更好,信噪比有了较明显的提升,均方根误差有较明显的下降,在变形监测数据处理中有很大的应用前景; 对于噪声密集,毛刺较多且数据波动较大的变形监测数据,改进的阈值函数能保留信号较多的有效细节,去噪以后的信号能够体现出建筑物变形的周期性变化,更加接近真实的数据,能更好地反映建筑物的沉降变形规律,给后期的变形预测提供了参考; 改进的阈值函数克服了硬阈值函数的不连续性,一定程度上避免了软阈值函数存在的恒定偏差问题,应用于变形监测数据去噪是可行的; 在同一种小波阈值去噪函数中,不同小波基的去噪效果存在差异,选择合适的小波基能够提升去噪效果。