热力学效应对高温高压调节阀空化的影响

何庆中1，刘 佳，陈雪峰，刘 惺1，徐红财，童思敏

(1.四川轻化工大学 机械工程学院，四川 自贡 643000；2.华夏阀门有限公司，四川 自贡 643000)

空化是高温高压调节阀在使用过程中常见的现象，产生区域主要集中在调节阀节流元件内。当介质经过高压差节流孔时，压力骤降至该温度的饱和蒸汽压以下，液态介质汽化产生空泡，并伴随着高流速冲刷在阀门零件上，造成汽蚀，甚至严重危害阀门的运行安全。现有针对调节阀空化流动的研究多是假设在等温条件下进行，没有考虑到高温介质的热力学特性。在高温高压调节阀中，高温水的物质属性(如密度、定压比热、饱和蒸汽压等)对温度变化非常敏感。介质发生降压空化时，会有大量的汽化潜热和能量转化，进而在空化区域形成明显的温度梯度，引起饱和蒸汽压的变化，对空化流动产生影响。因此开展高温高压条件下的调节阀空化研究具有非常重要的意义。

目前，对于空化热力学效应的研究主要集中在低温液氮和高温水两种介质中进行，而由于空化现象的复杂性，数值模拟方法是当前主要采用的研究方法[1]。王柏秋等[2]提出基于Rayleigh-Plesset方程的Singhal[3]空化模型所表达的物理内涵丰富，能够较好地反映空化问题的细节，在研究空化问题时被广泛使用。时素果等[4]将Singhal，Kunz，Ku-bota空化模型和液氮物理属性随温度变化的函数导入CFX软件中，结果表明翼型模型在热力学效应下的空化长度比等温工况下有所减少。王巍等[5]采用Singhal全空化模型并导入UDF函数，对不同温度流体绕翼型流动进行分析，结果表明空化区域温度降低引起当地饱和蒸汽压力降低，抑制空化的发展。季斌等[6]基于汽液传输方程提出了一种适用于高温水计算的空化模型，证明了该模型能更好地反应不同温度介质下的空化面积随温度变化的趋势。笔者为了研究高温高压调节阀的空化流动，选用Singhal提出的空化模型，并添加反映热力学效应的源项，源项大小与局部压力、温度、汽液体积分数等参数有关[7]。求解连续性方程、动量方程、质量输送方程并耦合求解能量方程，同时对反映热力学效应的参数逐步修正，以提高空化流场的求解精度。

1 计算方法和数值模型

1.1 控制方程

空化流动采用均质混合相模型，假定混合相由汽相和液相均匀组成，流体密度可变，且忽略液相和汽相之间的相对滑移运动。空化流动遵循基本的连续性方程、动量守恒方程、能量守恒方程分别为

(1)

(2)

(3)

式中：x,u分别为坐标分量和速度分量；ρm为混合相的密度；δij为克罗内克数；μ为混合相的动力黏度；μt为湍流黏度；h为混合相焓值；keff为有效传热系数；T为流体局部温度；SE为能量方程源项，即空化引起的流场能量改变，其大小等于汽液之间质量交换量与汽化潜热的乘积，其中

ρm=ρl(1-αv)+ρvαv

(4)

μ=μl(1-αv)+μvαv

(5)

式中：ρl，ρv分别为液相密度和汽相密度；αv为汽相体积分数；μl，μv分别为液相和汽相动力黏度。

1.2 空化模型

现有主流的空化模型都是基于质量输送方程，其基本表达式为

(6)

式中：Re为蒸汽蒸发率；Rc为冷凝率。

Singhal提出的全空化模型基于空泡动力学Rayleigh-Plesset方程，模型中包含了控制蒸汽产生和凝结的方式，同时考虑了汽液两相间的相变、湍流压力脉动以及不凝结汽相等因素。其蒸发率和凝结率的计算公式分别为

(7)

(8)

大量试验证明，湍动能对空化流有很大的影响，因此将汽化压力修正为

(9)

式中：KE为湍动能；τ为表面张力系数；Ce和Cc为两个经验系数，分别取0.02和0.01；Psat为当地饱和蒸汽压；fv为汽相的质量分数；fg为不凝结汽相的质量分数，在高温流体中，不可凝结汽相的质量近似为0，对空化的影响可忽略。

1.3 数值计算方法

以调节阀的节流套筒为研究对象，如图1所示，套筒上均匀分布若干节流孔，其承担了调节阀中绝大部分的压降，也是最容易产生空化的区域。

图1 节流套筒示意图Fig.1 Schematic figure of throttle sleeve

根据节流套筒的几何特性，相似换算后将其简化为单流道模型，计算域如图2所示。其中计算域进出口边界均为压力条件，壁面采用固定无滑移边界，一侧采用对称约束。对计算域进行网格划分并通过网格无关性验证，进一步提高网格数量对求解精度几乎无影响。

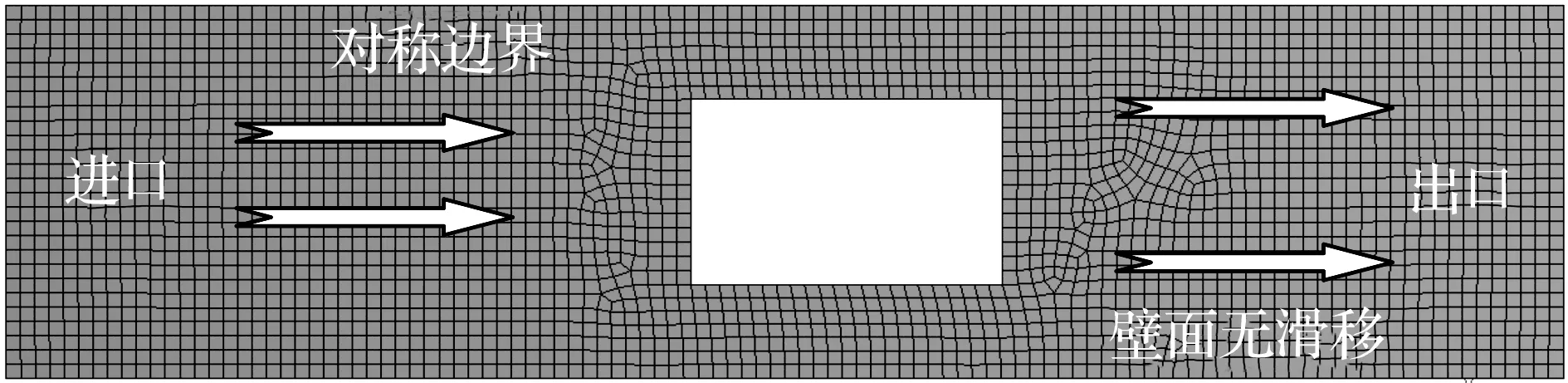
图2 计算域及网格Fig.2 Computational domain and mesh

对原求解器中的空化模型进行修正，嵌入自定义源项函数。同时设置计算对流离散项为高阶迎风格式，扩散项为差分格式，压力项采用PRESTO格式，耦合能量方程采用高阶迎风格式，输送方程采用QUICK格式，收敛残差精度为10-4。

2 计算结果及分析

2.1 热力学效应下的温度变化

考虑计算域发生空化而引起的温度变化[8]，以高温高压水为介质，设置初始进口压力10 MPa，出口压力4.8 MPa。假设水流初温分别为423，473，493 K，并设置相应的密度、导热率、定压比热等物性参数。同时考虑到介质在流动过程中发生的汽化潜热吸收和能量转化，以汽液两相的质量交换率和汽化潜热作为能量方程的源项，模拟计算域温度的动态变化，进而更加准确地预测空化的发生和发展[9-10]。

其中当水初温为423，473 K时，节流空化区域的温度云图如图3所示，云图中介质在流动路径上存在一定的温升情况，特别是在经过节流区域时，温升十分明显，此处也是空化集中区域。对计算域温度场进行量化，沿流动路径平均提取20 个数据样点[11]，如图4(a，b)所示，当来流水温为423，473 K时，空化区最高温度分别提升了1.3，1.85 K。

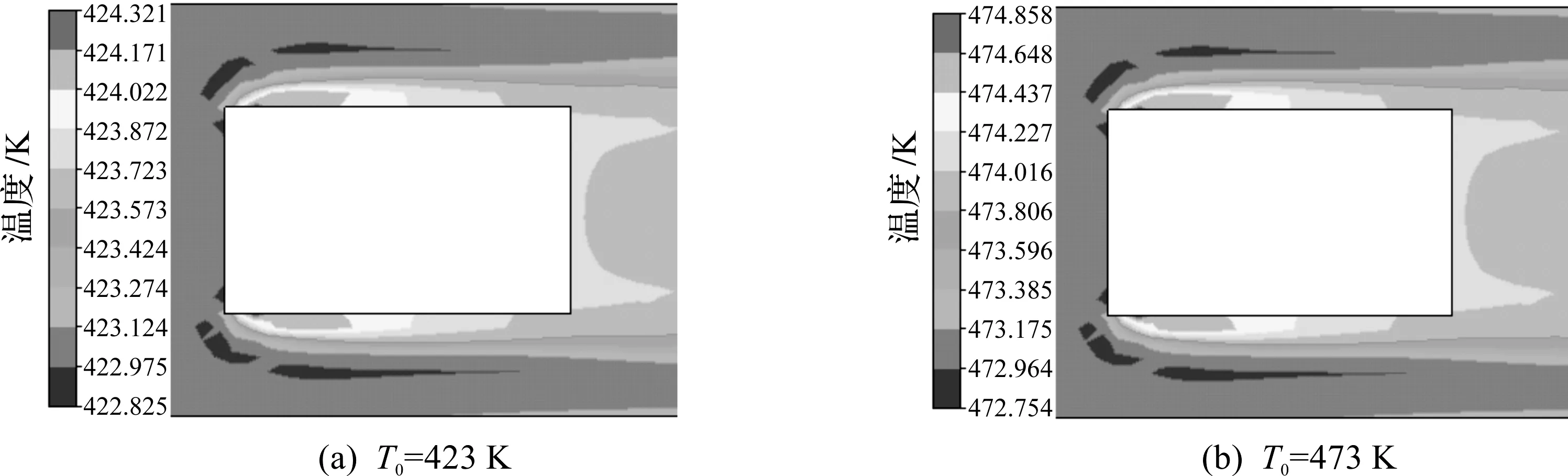
图3 计算域温度云图Fig.3 Temperature counter of computational domain

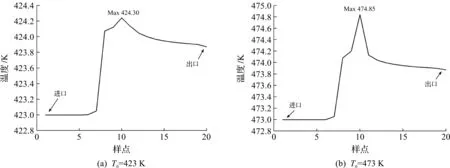
图4 计算域温度分布Fig.4 Temperature distribution of computational domain

提高来流水初温至493 K，计算域温度分布如图5所示，介质温度在最高点升至495 K，最大温差达2 K，但后续介质温度随着流动逐渐接近来流温度。由此可见：在相同减压系数下，水流温度越高，空化区域的温升量越大[12]。分析计算域温度上升的原因，可以从图6中T0=493 K的压力和速度分布看出[13]；在高温高压条件下，介质经过节流孔降压时，压力能转化为动能以及部分热能，因而出现压力减小，速度和温度有所提升的情况，这也符合文丘里效应的特征。同时，当介质压力骤降至当地饱和蒸汽压力Pv以下时，液相迅速向汽相转化，形成大量的汽泡，产生空化现象[14]。

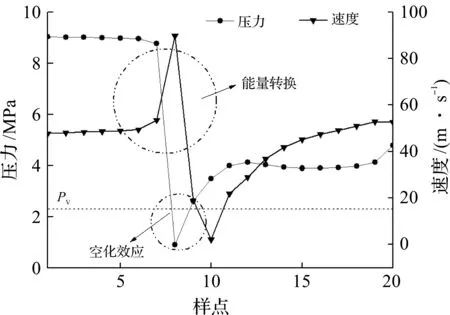
图6 T0=493 K计算域压力和速度分布Fig.6 Pressure and velocity distribution of computational domain(T0=493 K)

2.2 热力学效应下的空化体积变化

在高温高压水经过减压之后，节流区域的温度会出现小幅升高，引起汽化压力的升高，使得汽液两相之间质量输送量和能量方程源项增大，反映空化流场的参数不断修正。图7为汽化压力变化前后的汽相体积分布情况。如图7所示，汽化体积随着温度的升高而有所增大，说明在高温高压调节阀减压过程中，由于热力学效应的存在，促进了空化现象的发展[15]。图8为汽化体积量化曲线。如图8所示，在考虑热力学效应之后，汽化压力随温度变化，造成空泡体积增大，空化现象加剧。

图7 计算域汽化体积分数云图Fig.7 Contour of vapor volume fraction around computational domain

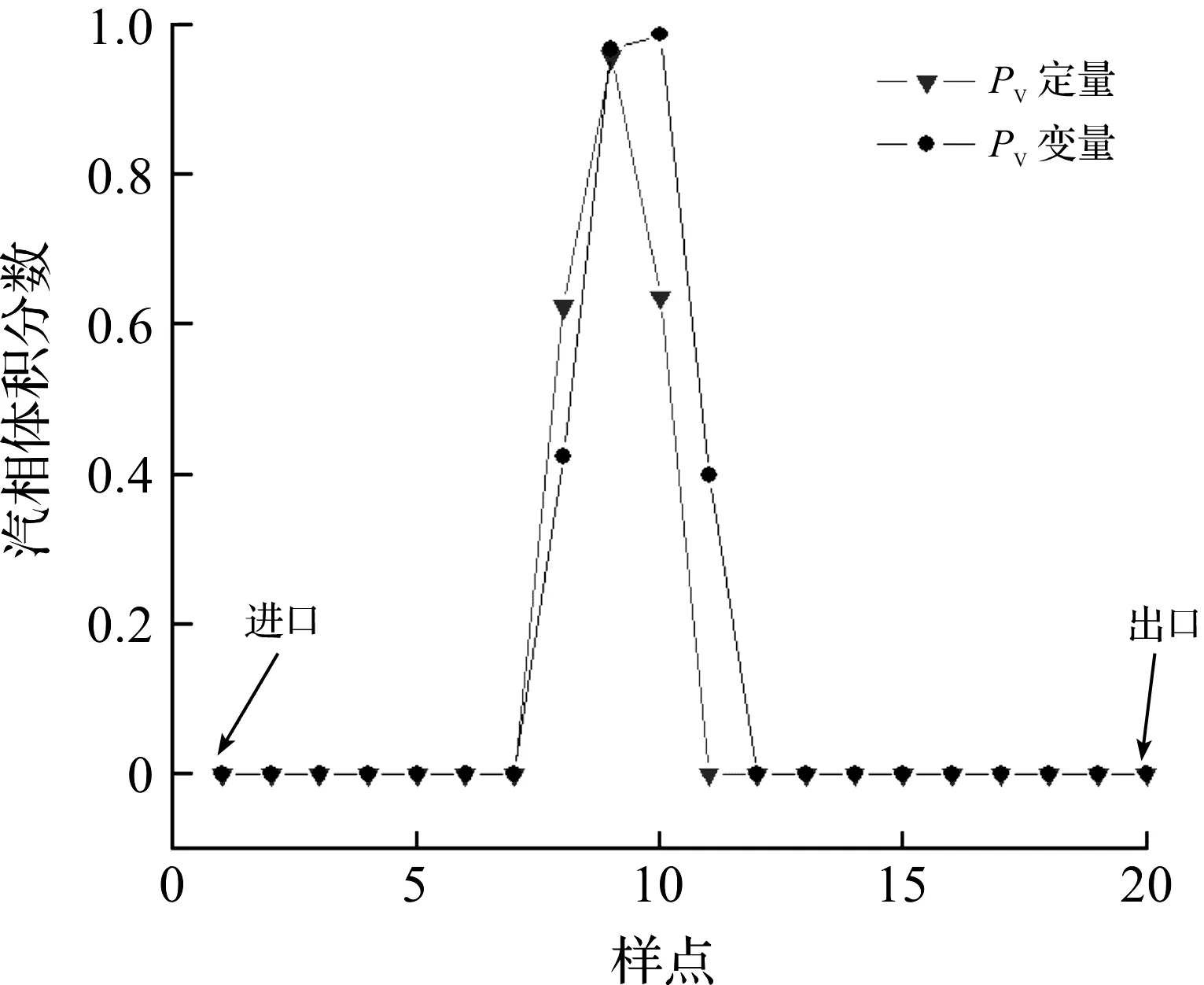
图8 不同汽化压力条件下汽相体积对比Fig.8 Comparison of vapor fraction at different Pv conditions

3 结 论

基于数值模拟方法，采用全空化模型并添加反映热力学效应的计算源项，分析了高温高压调节阀在节流过程中的空化发展情况，得出结论：在相同减压系数下的，随着介质温度升高，节流空化区域的温升量越大。同时，介质温度升高会引起局部饱和蒸汽压力升高，从而扩大空化发展的范围。综上，在考虑热力学效应后，通过添加源项函数对空化模型及相关参数进行修正，能有效提高空化流场的求解精度。