环境库兹涅茨曲线视角下河南省大气污染的分析

王 芳，邓文刚

(郑州大学 1.商学院;2.国际学院，河南 郑州 450001)

绿色良好的生活环境一直以来都是居民赖以生存的基本条件，其中，空气质量的好坏直接影响着人们的健康水平。但是，通过历史经验来看，任何地区的经济发展无不以环境的透支为代价。近几年，随着城市化进程的加快以及工业化的迅速发展，河南省的空气质量一直没有长期保持在较高的水平。党的十八大报告、“十二五”规划纲要以及2012年中央经济工作会议中明确指出应当注重经济社会与自然环境的协调发展，力求每一个城市都能成为宜居城市。[1]环境库兹涅茨曲线反映了环境质量与人均收入之间的关系，从理论上来说，污染程度随着人均收入的增加先提高后降低，但在实际当中两者之间有时却不会表现出这样的关系，污染程度甚至可能会随着人均收入的增加先提高、后降低、再提高、再降低，因此河南省的大气污染和经济发展之间具体是什么样的关系还有待于在实证分析中做进一步研究。

一、文献综述

传统的EKC曲线呈现出倒“U”型，这一点已经被国内外大多数学者所证实。例如Grossman和Krueger(1995)[2]、林伯强和蒋竺均(2009)[3]、黄炎和丁健(2016)[4]等。除此之外，一些学者在研究中还发现环境库兹涅茨曲线有时会呈现出“N”型、倒“N”型等类型。张乐勤等(2012)以动态测度的方式对安徽省1995—2010年的碳排放强度进行观测和分析，发现其EKC曲线表现为“N”型。[5]周小亮、吴武林(2016)在对福建省大气和水污染的分析中发现废气、废水的排放与人均收入之间呈现倒“N”型关系。[6]孙艳丽、李中轩(2017)在对许昌市工业“三废”的排放量的调查分析中得出了工业粉尘呈现倒“U”型曲线的右侧+正“U”型曲线的左侧的结论。[7]

在研究方法上，目前还没有一个统一的标准。任海军和刘高理(2014)以STIRPAT模型为基础对碳排放量进行了一系列的测度，并指出不同阶段的城市化进程中各因素对碳排放的影响存在着差异。[8]谢守红、蔡海亚、夏刚祥(2016)使用IPCC关于碳排放的测算方法，用脱钩模型对1980—2012年中国交通运输业的碳排放量进行了相关的分析。[9]因此，在今后的研究当中还应当注重不断地总结和归纳，找到普适性更强的研究方法。

综上所述，目前的研究大多打破了经典环境库兹涅茨曲线的假设，提出了许多新的不同类型的EKC曲线。但是，各地区的环境污染程度和经济发展的状况都不尽相同。为此，本文将在经典环境库兹涅茨曲线理论的基础上结合河南省自身的特点构建高次多项式模型进行实证分析，使研究方法具有一定的针对性和新意，并将根据河南省目前存在的一些环境问题给出相应的政策建议。

二、数据来源与模型设定

(一)数据选取

本文选取河南省1998—2017年共20年的时间序列数据，从历年的《河南省环境状况公报》上选取衡量大气污染的3个较为常用的指标：工业废气排放总量、二氧化硫排放量以及烟(粉)尘排放量。其中，工业废气排放总量的符号记为“INDGAS”，单位为“亿标立方米”；二氧化硫排放量的符号记为“SO2”，单位为“万吨”；烟(粉)尘排放量的符号记为“SD”，单位为“万吨”。

对于变量的选取，因为人均国内生产总值与大气污染具有较高的关联性，故取其作为解释变量，符号记作“PGDP”，单位为“元”。数据来源于历年的《河南省统计年鉴》。

将以上指标和变量进行对数化处理后的结果如表1所示。

表1 大气污染与经济增长的相关指标与变量汇总

(二)模型设定

根据现有的一些研究，环境库兹涅茨曲线的模型一般表现为二次多项式、三次多项式、四次多项式、对数二次多项式、对数三次多项式以及对数四次多项式等几种形式。出于对数据波动和复杂因素的考虑，本文选取对数四次多项式作为基本计量经济模型进行分析：

lnYt=α0+α1lnXt+α2(lnXt)2+α3(lnXt)3+α4(lnXt)4+μt

其中，lnYt表示各类环境污染指标第t年的数据的自然对数；lnXt表示人均国内生产总值第t年的数据的自然对数；μt表示随机误差项；αi(i=1,2,3,4)表示各个参数的待估系数。

对模型估计结果参数的讨论有如下几种类型：①α1=α2=α3=α4=0，表示大气污染与经济增长之间不存在关系；②α1≠0，α2=α3=α4=0，表示大气污染与经济增长之间存在单调递增或单调递减的关系；③α1=α2≠0，α3=α4=0，表示大气污染与经济增长之间存在单调递增或单调递减的关系；④α1<0，α2>0，α3=α4=0，表示大气污染与经济增长之间存在正“U”型关系；⑤α1>0，α2<0，表示大气污染与经济增长之间存在倒“U”型关系；⑥α1>0，α2<0，α3>0，α4=0，表示大气污染与经济增长之间存在正“N”型关系；⑦α1<0，α2>0，α3<0，α4=0，表示大气污染与经济增长之间存在倒“N”型关系；⑧在之前的基础上，如果α4≠0，那么所得的环境库兹涅茨曲线将不同于以上的形状，会呈现出一种连绵起伏的形态，称为“波浪型”。

三、实证分析

(一)平稳性检验

当时间序列不平稳时，在此基础上得到的回归有可能会是伪回归。为此，在建立模型之前，要先对各个变量的平稳性进行检验。本文选取使用较为普遍的ADF检验法，具体的检验结果见表2。

表2 ADF单位根检验结果

注：括号中的数字代表与检验值相对应的P值，“*”“**”“***”分别表示10%、5%、1%的显著性水平

由表2数据可看出，lnSD在原序列和一阶差分以及二阶差分的条件下都通过了5%或1%的显著性水平下的检验；lnPGDP在一阶差分和二阶差分的条件下分别通过了10%和5%显著性水平下的检验；其他变量在原序列的条件下均未通过检验，在一阶差分和二阶差分的条件下通过了1%显著性水平下的检验。由此可知，所有指标和变量经过处理均可变为二阶单整序列，因此能进行协整分析。

(二)协整分析

1.协整检验

经过平稳性检验后，对大气污染的各项指标与人均GDP之间是否具有协整关系进行检验，本文采用EG两步法对变量之间形成的残差序列项的稳定性进行检验。

第一步，分别对大气污染的3个指标与人均GDP之间进行一元一次回归，具体的回归方程如下：

lnINDGAS=2.7341+0.7339lnPGDP

(6.2814) (16.3217)

F=266.3977，R2=0.9367，n=20

lnSO2=5.0938+0.0466lnPGDP

(4.0368) (3.5778)

F=128.0813，R2=0.9286，n=20

lnSD=9.9465+0.5575lnPGDP

(12.7746) (6.9312)

F=48.0418，R2=0.7287，n=20

经过检验发现上三式的t检验和F检验均显著通过，并且从回归结果可以看出其可决系数分别为0.9367、0.9286、0.7287，这说明回归方程具有较好的拟合效果。

由表3数据可知，大气污染的指标与人均GDP之间所形成的残差序列均通过了5%的平稳性检验，这表明它们之间存在着长期的均衡关系。

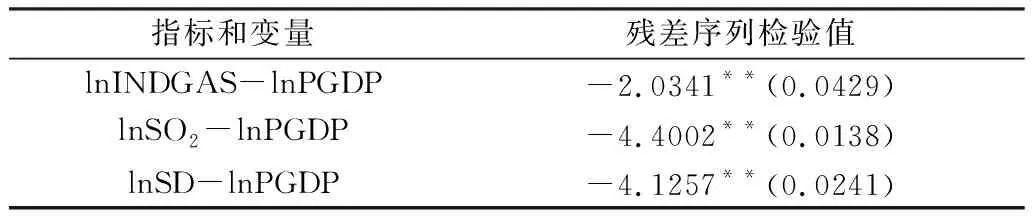
表3 大气污染指标与人均GDP的协整检验结果

注：检验是对各项指标和所有变量的二阶差分之间所形成的残差序列进行的平稳性检验，“*”“**”“***”分别代表10%、5%、1%的显著性水平

2.协整分析

经过平稳性检验和协整检验后，根据所选用的计量经济模型对大气污染的各项指标与人均GDP之间的关系进行参数估计，判定回归结果中t统计量值、F统计量值以及R2的大小，若不显著则剔除四次方项，接着对三次方方程进行参数估计。以此类推，直到选出合适的方程为止，表4列出了具体的参数估计结果。

表4 大气污染的各项指标与人均GDP之间的参数估计结果

注：括号中的数值为t检验的值，“*”“**”“***”分别代表10%、5%、1%的显著性水平

工业废气排放总量与人均GDP之间的方程为：

lnINDGAS=-4896.95+2062.81lnPGDP-324.82(lnPGDP)2+22.70(lnPGDP)3-0.59(lnPGDP)4

由此可知，工业废气排放总量与人均GDP之间属于四次多项式的关系，α1>0，α2<0，α3>0，α4<0。各解释变量的t统计量值分别为-3.96、3.98、-3.99、4.01、-4.03，均通过了显著性水平为1%的t检验。同时F统计量的值为153.24，说明F检验也十分显著。并且R2的值也较大，为0.9761，证明在较好的拟合效果下工业废气排放总量与人均GDP之间的关系呈现波浪型曲线的形态。

二氧化硫排放量与人均GDP之间的方程式为：

lnSO2=482.86-151.55lnPGDP+

16.62(lnPGDP)2-0.6(lnPGDP)3

由此可知，二氧化硫排放量与人均GDP之间属于三次多项式的关系，α1<0，α2>0，α3<0。各解释变量的t统计量值分别为2.62、-2.73、2.86、-3.00，均通过了显著性水平为1%的t检验。同时F统计量的值为17.95,说明F检验也十分显著。并且R2的值也较大，为0.7709，证明在较好的拟合效果下二氧化硫排放量与人均GDP之间呈现出倒“N”型的关系。

烟(粉)尘排放量与人均GDP之间的方程式为：

lnSD=-19.74+5.68lnPGDP-0.33(lnPGDP)2

由此可知，烟(粉)尘排放量与人均GDP之间属于二次多项式的关系，α1>0，α2<0。各解释变量的t统计量值分别为-1.77、2.42、-2.66，前两个变量通过了显著性水平为5%的t检验，后一个变量通过了显著性水平为1%的t检验。同时F统计量的值为35.69，说明F检验也十分显著。并且R2的值也较大，为0.8077，证明在较好的拟合效果下烟(粉)尘排放量与人均GDP之间呈现出倒“U”型的关系，这与环境库兹涅茨曲线的假定相符合。

三、结论

本文在“绿水青山就是金山银山”的时代背景下，选取河南省1998—2017年共20年的时间序列数据，通过将计量模型设成对数四次多项式的形式，用逐步回归法对河南省大气污染物的3个指标和人均国内生产总值之间的关系进行实证分析，得出以下结论：

(1)工业废气排放总量与人均GDP之间呈现波浪型关系。其中在可观测范围内模型的人均GDP只有一个EKC拐点35600元，大致出现在2013—2014年之间。在人均GDP低于35600元时，工业废气的排放量随人均收入的增长呈现出上升的趋势，这表明在当时的条件下由于省内总体生产力水平还尚未发展成熟起来，工业废气的排放随人均国内生产总值的增加而增加。当人均GDP超过35600元以后，工业废气的排放量呈现出下降的趋势，这表明在 “绿水青山就是金山银山”的号召下，各地纷纷提高了生态保护的意识，因此工业废气的排放量随人均国内生产总值的增加而日渐减少。

(2)二氧化硫排放量与人均GDP之间呈现部分倒“N”型关系。模型中人均GDP的两个EKC拐点分别为3655元和20688元，前者的出现时间并不在样本数据范围内，但可以推测大致在20世纪90年代中期，后者的出现时间则大致出现在2009年前后。在人均GDP达到3655元之前，二氧化硫排放量随着人均GDP的增加而下降；在人均GDP处于3655元到20688元的这段时期内，二氧化硫排放量随着人均GDP的增加而增加；当人均GDP超过20688元以后，随着各地对工业污染监测和管控力度的加强，二氧化硫排放量又重新开始减少。从中可以看出，尽管理论模型预测的曲线形状是倒“N”型，但是在现有样本的观测范围内模型更多呈现出的是倒“N”型曲线的右半部分，其中二氧化硫排放量与人均GDP的EKC拐点应当处于人均GDP为20688元的时候。

(3)烟(粉)尘排放量与人均GDP之间呈现倒“U”型关系。模型中人均GDP只有一个EKC拐点5465元，出现的时间大致在2000—2001年之间。在人均GDP尚未达到5465元的时候，烟(粉)尘排放量随着人均GDP的增加而增加，这主要是因为相对来说在旧有的工业生产条件下，烟(粉)尘的排放量在所有污染物中所占的比重较大。当人均GDP超过5465元以后，烟(粉)尘排放量随着人均GDP的增加而减少，这表明生产技艺在当时有了一定程度的提高，对于烟(粉)尘排放的控制也有了明显的进步。

四、政策建议

(1)提高能源的利用效率。燃煤、燃油等使用效率的低下是大气污染产生的一个重要原因，正是因为在以往的工业生产和居民生活中不够注重充分利用这些资源，才使得工业废气、二氧化硫以及烟(粉)尘等污染物的排放量与日俱增。因此，只有转变生产生活观念，最大限度地利用这些资源才能够在更大程度上降低污染物的排放量。当前河南省基本已经突破第二个转折点或者说EKC拐点，在中央政府的号召和新生产技术的支持下提高煤炭等能源的使用效率已是大势所趋，企业和居民家庭都应为建设资源节约型和环境友好型社会做出贡献。

(2)顺应历史的规律制定合理有效的减排目标。在过去的二十年内由于缺少历史的经验和实际的参考，我国的节能减排工作一直没有取得有效的进展。根据发达国家近几十年的污染治理工作中所产生的经验，碳排放量大致可分为三个阶段：碳排放积累阶段、碳相对减排阶段、碳绝对减排阶段。当前我国正处在并将长期处在相对减排的第二阶段，更要在未来长期内制定符合各地区实际情况的减排目标，力争早日进入绝对减排的第三阶段。

(3)增强城市的环境承载力。除了从能源使用的角度降低污染之外，客观上还应当在河南省内各大城市的环境承载力上加强重视和保护。河南省作为人口大省，近几年随着人口出生率的增加，在庞大的人口基数下环境承载力逐渐下降。为此，更要贯彻落实科学发展观全面协调可持续的原则在改善居民生活水平和条件的同时兼顾资源的合理开发与城市环境的保护，促进彼此之间的协调发展，从而增强城市的环境承载力。

(4)加强大气污染的综合治理。大气污染需要从经济、行政、法律以及思维观念等多个方面着手进行综合的整治，在加快城镇化进程的同时应当提高对各项环境标准的相应的监督力度和执行力度，做到发展与保护同步进行。除此之外，推动产业结构的升级与战略性调整也是不可忽视的重要举措，要想打造“低碳型经济”需要以更多的高新技术产业取代旧有的高污染的产业，实现第二产业向第三产业的转型升级。最后，要向居民和企业传递可持续发展的环保意识，促使政府与民间在大气污染的防治和环境保护的进程中实现良好的互动和反馈，最终实现改善空气质量、打造绿色城市的目标。