临近燃气管道的爆破质点峰值振速预测
2020-05-30陈宏涛程贵海
陈宏涛,程贵海
(广西大学资源环境与材料学院,南宁 530004)
爆破产生的光、热、气以及振动、飞石等都会对附近物体造成危害。其中,爆破振动是最主要的危害[1]。它不仅威胁附近地面上建(构)筑物的安全,也影响地下井巷和地下管道,尤其是地下燃气管道的安全。
管道运输是目前天然气普遍且重要的运输方式,我国目前已建成的燃气、燃油管道长度已突破17万km。特别是在燃气资源集中的西南地区,管道的铺设非常密集[2]。若因爆破施工导致燃气泄漏,引起火灾或者爆炸,损失将难以估量。因此,对临近燃气管道的爆破振动更应该进行严格控制。国内已有许多学者对爆破施工临近管道的情况进行了研究。陈虎林等[3]通过数值模拟等方法,研究了在充满介质的普通金属运输管道外置爆破荷载的情况下,管道内部的振速峰值、衰减规律以及传播规律等。姚安林等[4]通过研究炸药爆破对地下深埋管道破坏的影响,得出当爆心距R保持不变时,管内质点的振动速度衰减规律不会有明显的变化,但是随着单段最大装药量Q的增加,振动速度峰值增大;相反,当单段最大装药量Q不变时,管内质点振动持续时间不会有明显变化,但是随着爆心距R的增加,管内质点振动速度峰值会降低。
南宁某水利枢纽疏浚工程爆破区临近下埋燃气管道。因此利用线性回归与非线性回归方法,对燃气管道的振动进行了分析,得到了适用于该工程振动衰减规律的经验公式,准确预测了爆破作业下埋燃气管道的质点峰值振动速度,对于优化该工程后续爆破具有指导意义。
1 爆破质点峰值振速预测模型
国内外许多学者对爆破质点峰值振速进行了研究。我国应用最为广泛的是前苏联科学院地球物理研究所M.A.萨道夫斯基的爆破振动速度预测经验公式[5]:
(1)
式中:Q为最大单段药量,kg;R为爆心距,m;K、α为与爆破点地形、地质条件有关的系数与衰减指数。
许多工程实践证明,萨氏公式用来预测爆源与测点位于同一水平时,其预测精度较高,但当爆源与测点具有一定的高程差时,其预测精度将会大大降低。唐海等[6]通过相关理论研究分析,将高程差与萨氏公式相结合,得出了考虑高程效应的爆破振动峰值速度预测模型:
(2)
式中:K2为地貌影响因素;β为高程差影响因素;H为高程差,m。
本文所讨论的工程实例测点位置处下埋燃气管道与爆破作业爆源中心点的高程差相对较小,所以不考虑高程差的影响。
2 工程实例
该水利枢纽工程位于邕江干流南宁河段下游青秀区仙葫开发区牛湾半岛处,上距老口航运枢纽74 km,下距西津水电站124 km。
该工程需要在保证南宁市防洪排涝安全的前提下,适当抬高江河段的城市景观水位,以改善南宁市水环境,解决西津至老口河段航运水位衔接问题,同时兼顾水力发电。
按库容划分,该工程属于大型水库,枢纽工程等级为Ⅱ等,正常蓄水位67 m,总库容7.1亿m3,电站装机容量57.6 MW,为灯泡贯流式机组,平均发电量2.206亿kW·h。建设项目主要有拦河坝、13孔闸坝、发电厂房及进场交通公路。
2.1 地质情况
该工程地质主要由第四系残坡积土层、全风化硅质岩夹泥岩和底部灰岩构成;岩性主要由黏土(第4层)、含有砾土(第5层)、黏土(第6层)、含碎石黏土(第6①层)、红黏土(第6②层)及全风化硅质岩夹泥岩组合而成。
依据南宁水文站相关统计资料,邕江干流南宁河段平均输沙量953万t,最大年输沙量2 260万t,最小年输沙量299万t,平均含沙量0.26 kg/m3。
2.2 爆破环境
该工程右岸护坡于里程右护1+150.00至右护0+917.00段施工,段处在燃气公司D500高压燃气管道高压北线4+700段200 m的安全保护距离内,右护1+096.00处距离燃气管道60 m,燃气公司的D500高压燃气管道高压北线4+700段属于南宁市供气环网,管道埋深1.5 ~ 2 m,压力约4 MPa,正式通气时间为2014年2月。
随着爆破点越来越靠近燃气管道,爆破产生的振动直接威胁到燃气管道的安全,如何保证不伤及燃气管道是该工程的一个难点。爆破区域环境及测点布置如图1所示。

注:①~⑦表示1#~7#监测点
图1 爆区环境及测点布置
Fig.1 Surrounding of blasting zone and layout of measuring points
2.3 爆破参数
该工程爆破是在右坡间距67 m的两处位置进行疏浚挖深处理,在0+850方位处共布置47个炮孔,钻孔直径为90 mm,孔深3~6 m,孔距2.1 m,排距2.3 m,炮孔超深1 m。采用梅花形布孔方式,使用直径70 mm 2#岩石硝铵乳化炸药;利用导爆管雷管引爆,2孔1响,间隔50 ms,孔内总共880 ms,15段起爆,同段最大起爆药量14 kg。在0+917方位处,共布置26个炮孔,钻孔直径90 mm,孔深3~5 m,孔距2.2 m,排距2.5 m,采用梅花形布孔方式,使用直径70 mm 2#岩石硝铵乳化炸药,利用工业电子雷管引爆,逐孔起爆,起爆间隔50 ms,同段最大起爆药量18 kg。采用人工连续装药。
3 爆破振动监测结果与回归分析
3.1 测点布置
燃气管道布置在既有公路之下,在距离导爆管雷管爆区242.3 ~ 292.5 m和距离工业电子雷管爆区100.5 ~ 140.4 m的燃气管道正上方,布置4个测点(见图1中的4#~7#测点),采用中科测控研制的TC-4850爆破振动记录仪(见图2)进行监测记录。由于需要分析数据与建立数学模型,所以同时监测新建边坡的振动数据(见图1中的1#~3#测点),使分析更为准确与可靠。

图2 测振仪安装
Fig.2 Installation of vibration measuring instrument
3.2 监测结果
各测点测得的爆破质点峰值振速、主振频率数据如表1所示。

表1 各测点峰值振动速度
3.3 回归分析
3.3.1 线性回归分析
根据爆破振动的数据,利用最小二乘法将萨氏公式进行回归处理,左右两边取对数得:
(3)
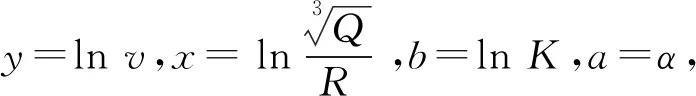
y=ax+b
(4)
式中:Q,R,v是已知的,所以y和x是已知的,通过回归计算可以确定b和a值,也就对应确定了K和α值。
利用最小二乘法可以求出a和b的值,计算公式为
(5)
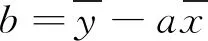
(6)
K=eb
(7)
在线性回归分析时,还要进行相关系数r的计算,相关系数r表征转换后线性方程预测振速准确性的高低程度大小。r的绝对值越接近1,相关程度越高,预测方程就越准。
相关系数的求解公式:
(8)

取表1各组数据中的最大振速值进行回归分析,结合式(3 ~ 8)进行最小二乘法计算。具体计算结果如表2所示。
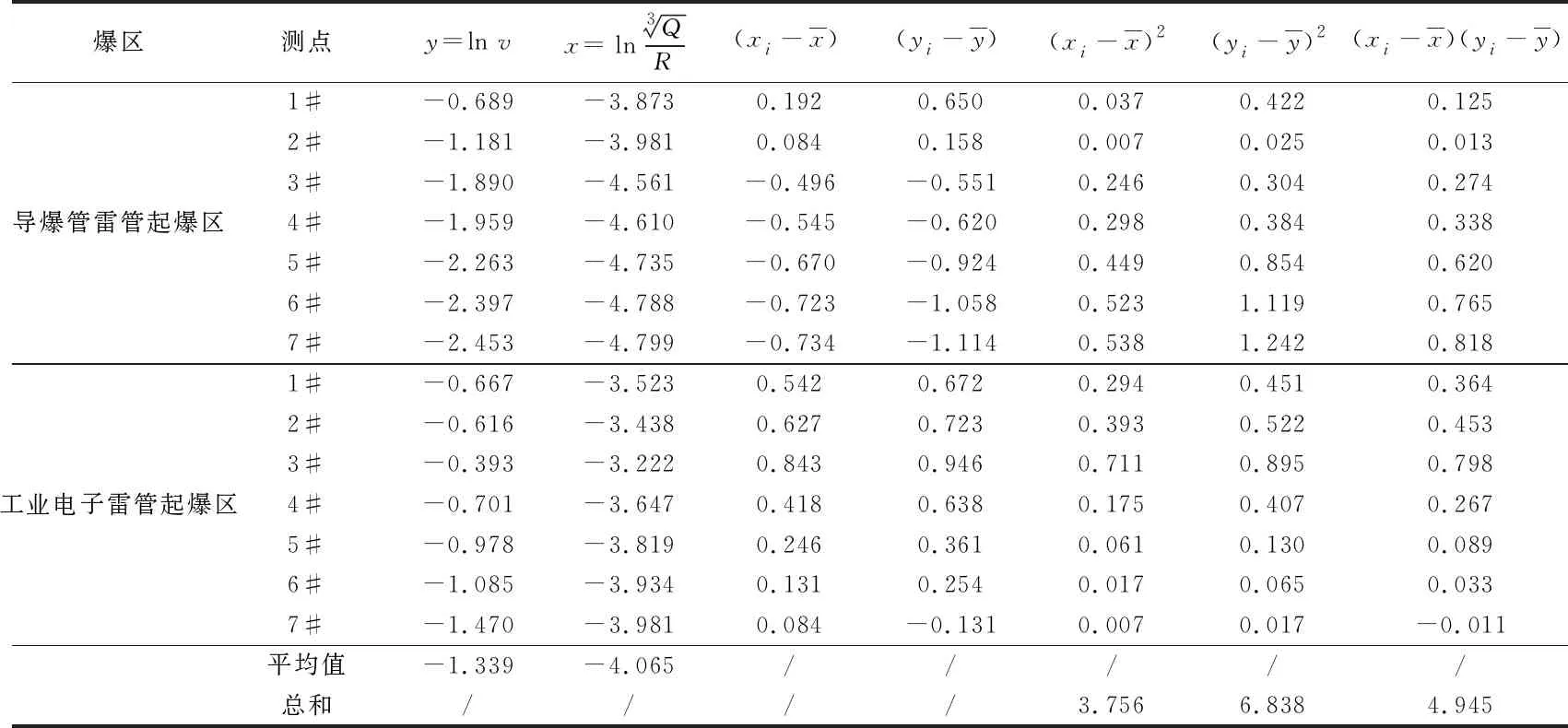
表2 振速回归计算结果
计算得a=1.317,b=4.013,所以K=eb=55.307。则回归后的萨氏公式为
(9)
线性回归相关系数r为0.976,表明此回归方程可以准确地预测最大振速的衰减规律。
采用式(9)线性回归得到的v预测值如表3所示。
3.3.2 非线性回归分析
根据实测爆破振动数据,采用1stOpt数据处理软件进行非线性回归分析,根据软件分析结果,得知萨道夫斯基公式中的K值为24.732,α值为1.101。所以,预测模型为
(10)
采用式(10)非线性回归得到的v预测值如表4所示。
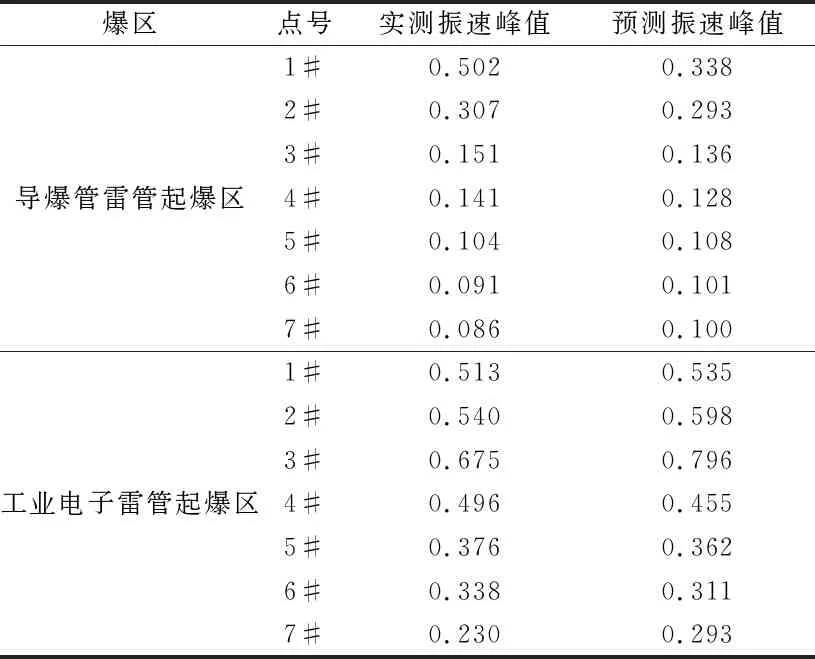
表3 线性回归预测值

表4 非线性回归预测值
3.4 结果分析
1)导爆管雷管起爆的线性回归预测值与实测值的对比如图3所示。

图3 导爆管雷管起爆的实测振速峰值与线性回归预测值
Fig.3 Linear regression predicted value and measuredPPVinitiated by nonel detonators
2)工业电子雷管起爆的线性回归预测值与实测值对比如图4所示。

图4 工业电子雷管起爆的实测振速峰值与线性回归预测值
Fig.4 Linear regression predicted value and measuredPPVinitiated by industrial digital detonators
3)导爆管雷管起爆的非线性回归预测值与实测值的对比如图5所示。

图5 导爆管雷管起爆的实测振速峰值与非线性回归预测值
Fig.5 Nonlinear regression predicted value and measuredPPVinitiated by nonel detonators
4)工业电子雷管起爆的非线性回归预测值与实测值对比如图6所示。
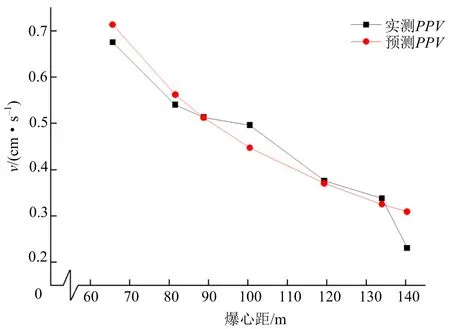
图6 工业电子雷管起爆的实测振速峰值与非线性回归预测值
Fig.6 Nonlinear regression predicted value and measuredPPVinitiated by industrial digital detonators
从以上对比结果可知,在误差允许范围内,回归分析的预测振速值与实测振速数据相差不大,但是非线性回归分析相比于线性回归分析精度更高,非线性回归分析模型的相对误差为5.44%,线性回归分析模型的相对误差为6.38%,结果更可靠,能较好地反应该工程的爆破振动传播规律。而工业电子雷管爆区和导爆管雷管爆区的峰值振动大小都随着爆心距的增加而减小,主振频率在爆心距低于100 m时变化较为明显,当超过100 m时频率基本不变。工业电子雷管爆区由于其具有精准的延时设定,所以其相对于导爆管雷管爆区的振动较小,降振效率较高,爆破振动主频较大,对保护燃气管道更具有积极意义。
目前国内关于爆破对管道定量影响的具体分析,还没有形成统一的权威理论。虽然多以安全振动速度为判断标准,但在具体安全尺度判断标准上,还有较大分歧。以振动速度2.5 cm/s和3.0 cm/s作为安全振动速度是管道行业暂时的主流看法,川气东送管道曾有人提出更为严格的2.0 cm/s的要求。然而,到底是3.0、2.5或者2.0 cm/s,还没有定论。国家在编制天然气保护法时,把天然气管道按照一般民用建筑来考虑,振动速度为2.5 cm/s作为标准。中石油川气东送分公司的王振洪[7]结合大量的文献,对比、分析法律法规、技术规范、工程实例、管道抗震能力等,最终提出2~6 cm/s的安全振速判据。
在本工程中,结合该水利枢纽现场实际情况,最终决定采用2.5 cm/s的安全振速,这也是在法规允许的范围之内。
4 结语
1)当环境不复杂时,在忽略爆破中心与测点的高程差的情况下,利用传统的萨氏公式进行爆破振动预测的研究,能较好地反应振动传播规律。
2)利用回归分析得到的爆破振动预测模型能较好地预测实际爆破振动峰值大小,无论是线性回归还是非线性回归都能较好地拟合预测振速峰值,非线性回归凭借着其5.44%的相对误差,使得它更加适合本工程的拟合。
3)工业电子雷管具有延时精度高,线路连接方便等优点,被广泛应用于工程爆破中。在该工程中采用工业电子雷管设置起爆网路,可以很好地减弱爆破振动对临近燃气管道的影响。
4)通过对国家天然气保护法以及相关文献资料对比研究,结合该水利枢纽工程的实际情况,此次爆破振速小于安全振动速度2.5 cm/s,没有对燃气管道产生任何危险。
