差压式流量计测量脉动流量方法研究

张永胜, 张毅治, 刘彦军

(北京长城计量测试技术研究所, 北京 100095)

1 引 言

差压式流量计[1]一般以孔板、文丘里管、喷嘴或其它形式的节流元件形成差压,进而计算流体流量。差压式流量计由于其结构简单、无可动部件等特点而广泛应用于测量封闭管道中单相稳定流体的流量,常用于测量空气、天然气、水等流体的流量。差压式流量计是最为传统且应用广泛一种流量测量装置,该类流量计的准确测量是以平稳流动为基础,当测量流体压力、速度随时间呈周期变化情形时,以稳态流的计算方法直接求取脉动流量将因遗漏流量导数项而引起较大测量误差[2～4]。而脉动流广泛存在于工业管路中,由于旋转式、往复式或可运动传送设备的使用,管道中流量控制设备的周期振荡,以及流程中工艺设备的特定要求,众多因素都会导致流体产生脉动流[5～8]。ISO 5167中明确规定差压式流量计不适用于脉动流的测量。

本文以经典文丘里管[9]为研究对象,通过FLUENT软件[10]对文丘里管在正弦脉动流下的流场进行仿真计算,分析了单路差压计算脉动流量时由导数项引入的测量误差,提出了基于双路差压的脉动流量测量方法,并利用仿真结果证明该方法的有效性。

2 脉动流量计算方法

2.1 脉动流理论模型

在脉动流状态下,假设流体流过节流件为一维流动[11,12],流量计内流动运动方程为:

(1)

式中:u为流向速度;t为时间;x为沿流向坐标;ρ为流体密度;p为压力。

由于质量流量qm可由式(2)表示,则式(1)可进一步表示为式(3)。

qm=ρAxu

(2)

(3)

式中Ax为x处管道横截面积。

假设节流件上游取压孔处于截面1位置,坐标为x1;下游取压孔处于截面2位置,坐标为x2;在截面1和截面2之间沿流线对式(3)进行积分,可得:

(4)

式中:A1和A2分别是截面1和截面2的截面积;Δp为截面1和截面2之间压差;C为节流件流出系数。

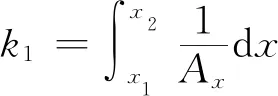
(5)

2.2 双路差压流量计算方法

在实际情况中流量导数项无法确定,传统的通过两截面之间单路差压计算流量的方法无法计算瞬时脉动流量,可通过测量两对截面之间双路差压,消除流量导数项的影响,进而计算瞬时脉动流量。

在收缩段前后各取2个截面,分别定义为截面Ⅰ、截面Ⅱ、截面Ⅲ和截面Ⅳ,如图1所示。4截面沿轴向的坐标分别是xⅠ、xⅡ、xⅢ和xⅣ。截面Ⅰ与截面Ⅲ内径相同,截面Ⅱ和截面Ⅳ内径相同,截面Ⅰ和截面Ⅱ之间流出系数为C1,截面Ⅲ和截面Ⅳ之间流出系数为C2。

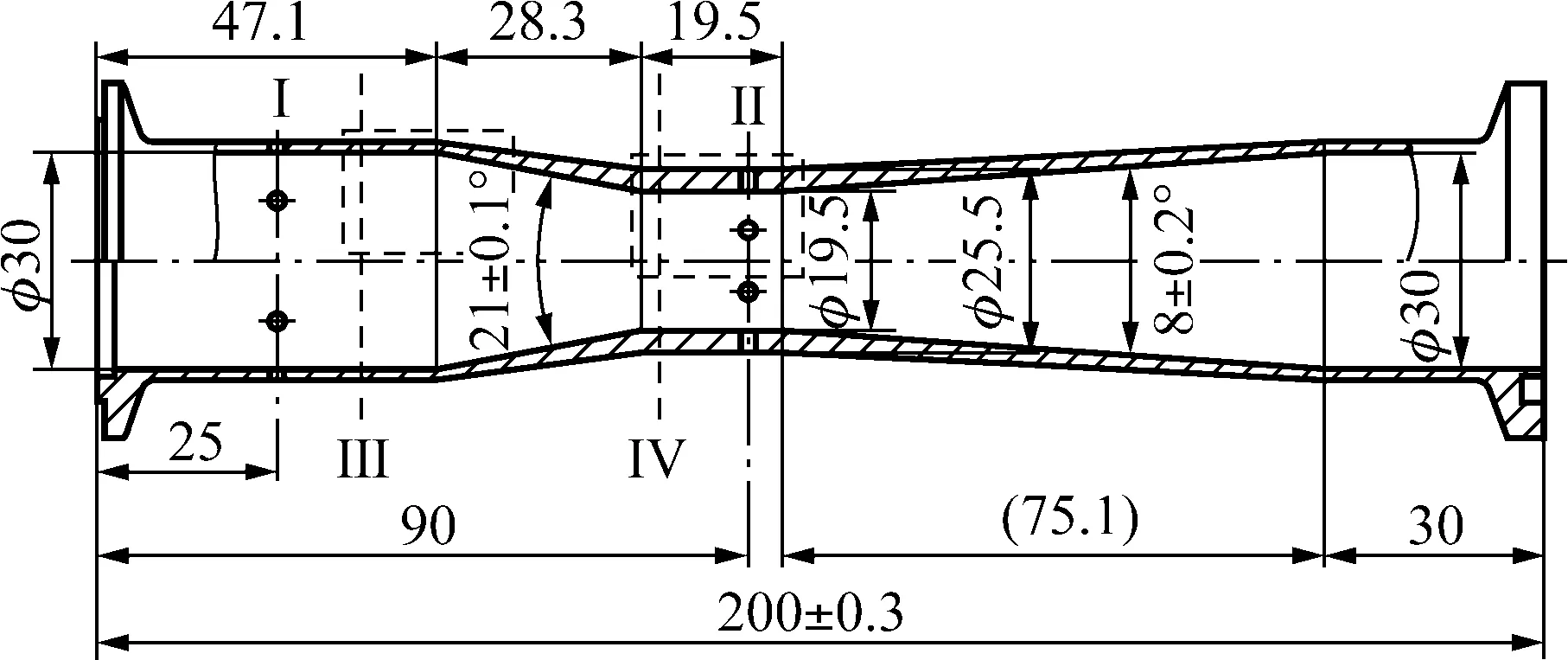
图1 文丘里管几何模型

在截面Ⅰ和截面Ⅱ之间,截面Ⅲ和截面Ⅳ之间具有如式(6)和式(7)所示关系。

(6)

(7)

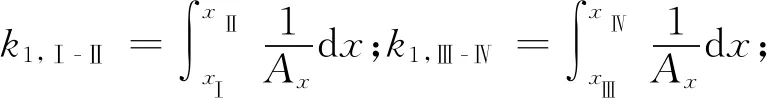
联立式(6)和式(7),消除流量导数项,可得质量流量与双路差压的函数:

(8)

3 流体仿真验证

3.1 几何模型

本文以文丘里管为对象,利用FLUENT软件进行流体仿真,获得两对截面间双路压差,对脉动流量计算方法进行验证。

图1所示的文丘里管进出口内径D=φ30 mm,喉径d=φ19.5 mm,直径比β=0.65,以进口截面中心为坐标原点,截面Ⅰ、截面Ⅱ、截面Ⅲ和截面Ⅳ这4截面坐标分别是xⅠ=25 mm、xⅡ=90 mm、xⅢ=46 mm和xⅣ=78 mm。

3.2 流体仿真模型

利用ICEM软件进行几何建模,忽略重力因素影响,基于文丘里管内流场轴对称特性,建立二维轴对称几何模型并进行网格划分。文丘里管上游设置10倍长直管段,下游设置5倍直管段。仿真模型壁面设置5层边界层网格,中心区域为三角非结构化网格。

仿真中选用标准k-ε湍流模型,选用液体水作为流体介质。设置下游直管段出口为自由出流条件,直管段及文丘里管壁为静止壁面;上游直管段入口为速度入口,通过UDF函数定义,可计算得到入口流速。

qm=q0+Aq0sin(2 πft)

(9)

(10)

式中:qm为瞬时质量流量,kg/s;q0=2 kg/s为质量流量平均值;A为脉动幅度;f为脉动频率;t为运行时间,s;Vt为瞬时入口速度平均值,m/s;ρ为流体密度,kg/m3;Ain为上游直管段入口截面积,m2。

3.3 单路差压流量计算误差

由稳态流动下仿真结果,可获得截面Ⅰ和截面Ⅱ之间流出系数C1=0.981 5,截面Ⅲ和截面Ⅳ之间流出系数C2=1.007。进一步可获得k1,Ⅰ-Ⅱ=141.75,k2,Ⅰ-Ⅱ=4 788.9,k1,Ⅱ-Ⅲ=71.856,k2,Ⅲ-Ⅳ=4 549.4。

稳态流动下,质量流量qmc可由式(11)计算:

(11)

正弦脉动流情况下,流量导数可由式(12)表示,若直接通过式(11)计算瞬时质量流量引入的导数项误差通过式(13)计算:

(12)

(13)

表1所示为7个工况单路差压计算流量误差数据。其中Ep-max表示误差上限,En-max表示误差下限。

表1 单路差压计算流量误差表

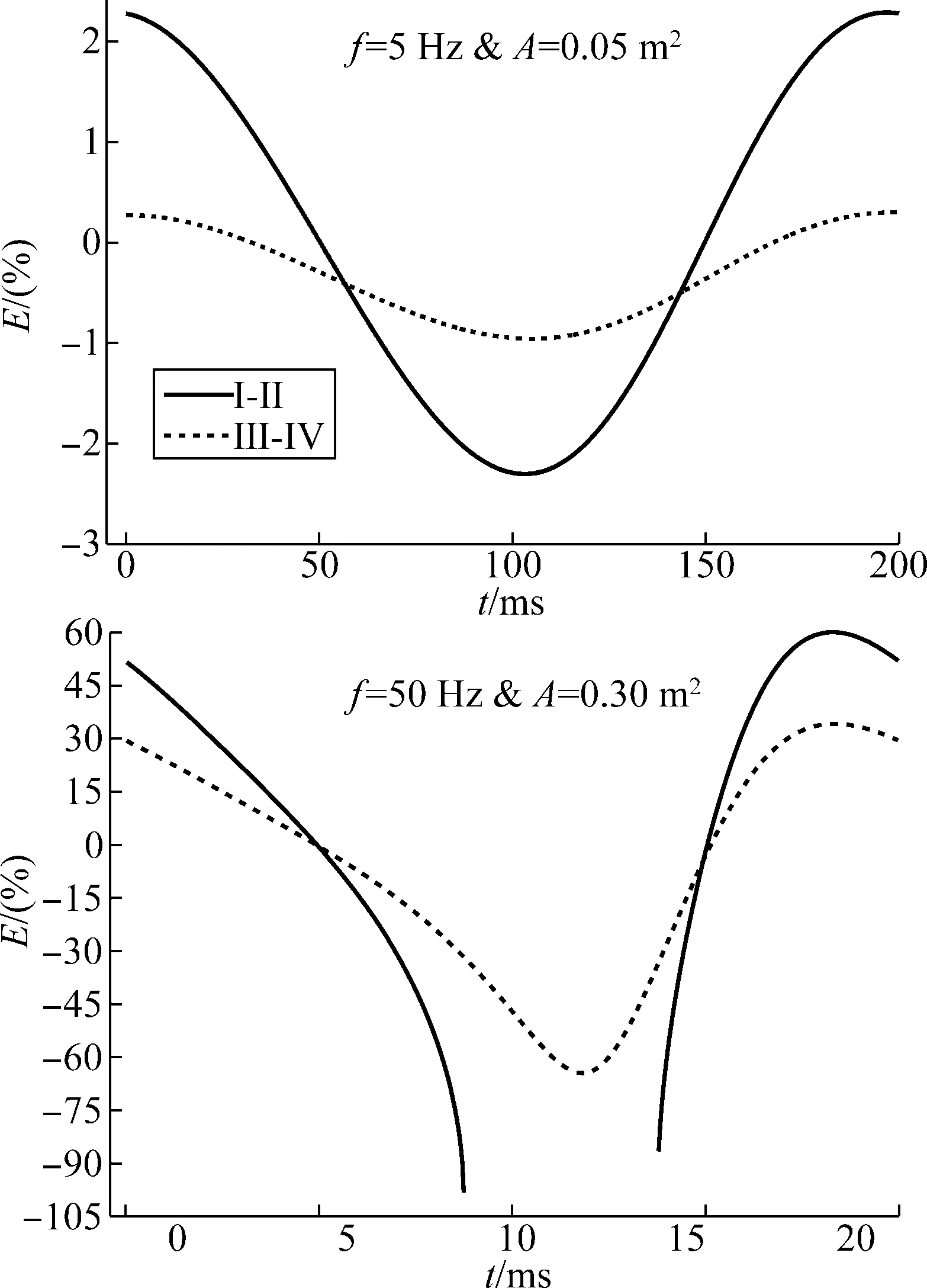
图2 单路差压流量计算误差曲线

图2是工况1和工况7单路差压流量误差曲线。表1中“×”位置和图2(b)中曲线中断处是由于ΔpⅠ-Ⅱ为负值造成。通过ΔpⅠ-Ⅱ和ΔpⅢ-Ⅳ计算瞬时流量,对应时刻截面Ⅰ-Ⅱ和Ⅲ-Ⅳ误差绝对值只有2个时刻相等,其余前者均大于后者。通过ΔpⅠ-Ⅱ计算脉动流量误差上限可达60%,误差下限最大可达-100%,甚至差压为负值导致无法计算;通过ΔpⅢ-Ⅳ计算脉动流量误差上限可达34%,误差下限最大可达-65%。因此减小k1,可有效降低由于遗漏导数项引入的脉动流量计算误差。

3.4 双路差压流量计算

基于式(8),利用ΔpⅠ-Ⅱ和ΔpⅢ-Ⅳ计算瞬时脉动流量,表2是双路差压脉动流量误差数据。图3是工况1和工况7双路差压流量计算误差曲线。图4是脉动流量计算误差带分布。

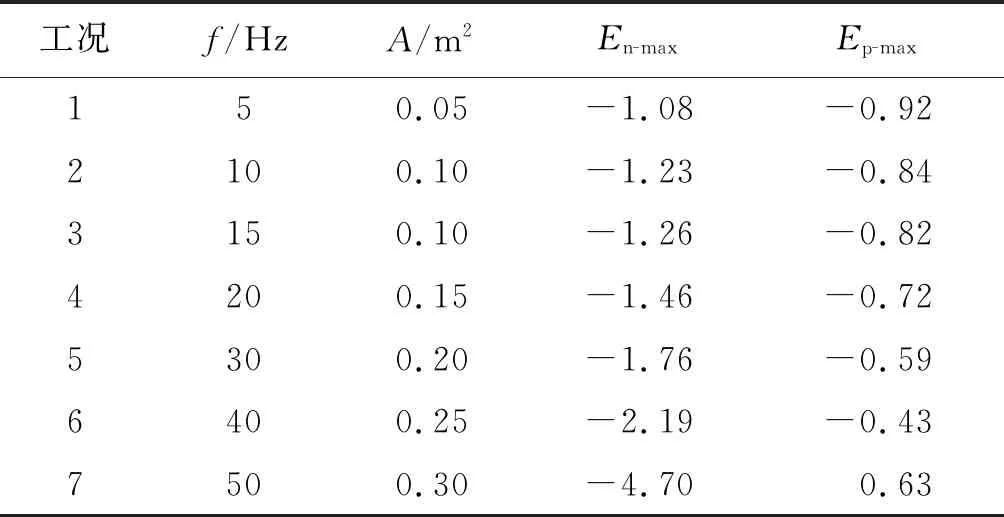
表2 双路差压计量流量误差数据表

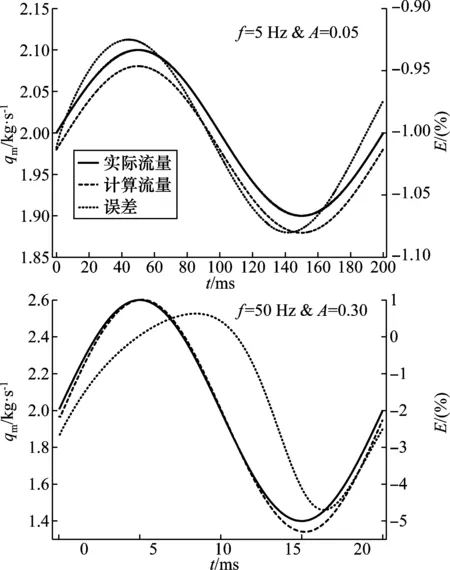
图3 双路差压流量计算误差变化曲线

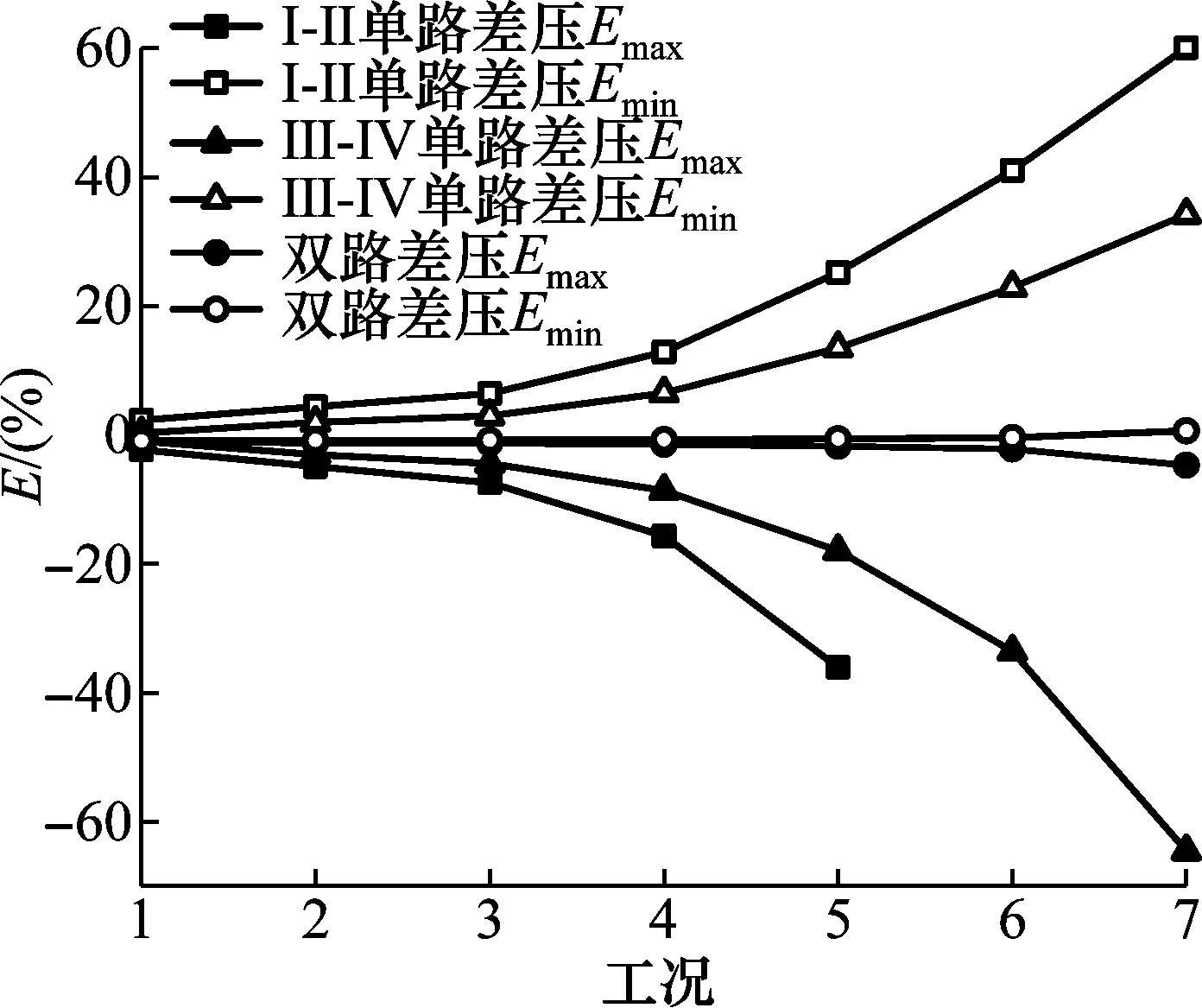
图4 脉动流量计算误差分布

通过双路差压计算脉动流量,可明显降低误差上限,提升误差下限,使得误差带变窄,在高频率大幅值下尤其显著。相对于双路差压计算流量,通过ΔpⅠ-Ⅱ计算流量的误差带宽度最小,为单路的1/24;通过ΔpⅢ-Ⅳ计算流量的误差带宽度最小,为单路的1/8。

4 结 论

研究中针对差压式流量计测量脉动流量时由导数项引入的计算误差,提出了采用双路差压消除导数项的计算方法,并以文丘里管为研究对象利用流体仿真进行验证分析,得到以下几方面结论:

1) 通过单路差压采用稳态流量公式计算脉动流量,由于遗漏流量导数项分量,造成很大影响,误差极值可达100%,测量误差带覆盖-100%～+60%,甚至由于差压为负值而无法进行计算。

2) 通过双路差压建立的微分方程组可有效消除导数项影响,脉动流量计算误差极值为4.7%,误差带分布覆盖-4.7%～0.6%,误差带明显收拢。

3) 建议对双路差压计算脉动流量方法在理论和试验方面进行进一步深入研究,验证该方法的有效性和可行性。