东印度洋海域最优深度基准面模型构建

姜传苓,付延光,周兴华,陈义兰,王永康

(1.山东科技大学 测绘科学与工程学院,山东 青岛266590;2.自然资源部 第一海洋研究所,山东 青岛266061)

海底地形测量成果是船舶航行、海上平台建设等海上活动的基础[1]。随着多波束、机载激光和重力水深反演等多种关键技术的应用,测量水深的数据呈现海量化的发展趋势,数据观测精度也在不断提高,进行多种水深数据的融合可有效提高区域海底地形的精度、分辨率和覆盖率。从而使得多源数据的融合问题成为目前研究的热点,其中应优先解决的问题是基准的统一。

作为我国海底地形测量的深度起算面,深度基准面是由相对于平均海面的垂直差距来确定其在垂直方向中的位置[2]。目前,深度基准面模型是以潮汐模型为基础,结合深度基准值确定算法实现的,其精度主要取决于潮汐模型的精度。随着潮汐模型的不断发展,深度基准面模型在分辨率、精度等方面得到逐步完善。但是,受构建方式、近海地形等因素的影响,全球潮汐模型在不同海域具有一定的精度差异。

深度基准面的形式多种多样,不同国家或地区采用的基准面不同,如中国采用理论最低潮面,英国采用最低天文潮面等,同时深度基准面的定义及算法不一致。许军等[2]针对理论最低潮面定义算法中的长周期改正与浅水改正部分进行了修订,但在部分验潮站仍存在浅水改正量无法获得最小值的问题;高秀敏等[3]对TPXO7.2和GOT00.2等全球潮汐模型在南海海域的精度进行了评估;付延光等[4]利用验潮站数据进行中国近岸海潮模型的精度评估。但随着潮汐模型和深度基准面算法的发展,由潮汐模型构建的深度基准面模型的精度越来越高,目前并没有针对最新的潮汐模型建立的深度基准面模型的精度进行分析,且没有建立模型进行大范围海域的研究等。

国内外对印度洋在水深测量数据融合方面的研究较少,尤其是针对东印度洋海域的深度基准面的研究更少。本文的研究区域为印度洋东部海域,包含孟加拉湾、马六甲海峡区域等海域及苏门答腊岛(88°～103°E,2°～22°N),通过长期验潮站实测数据及卫星测高数据的反演结果,对全球潮汐模型在印度洋东部海域的精度进行评估,在此基础上提出印度洋东部海域的深度基准面的最优模型,为印度洋东部海域进行多种水深数据融合提供数据基础。

1 实测数据及潮汐模型

1.1 验潮站数据

本文选取了印度洋东部海域的13 个长期验潮站,概略位置如图1所示,每个站具有6 a以上的逐时潮位观测数据,其中5个验潮站达到28 a,具体信息见表1。表1中,F表示潮汐类型,可由公式F=(H(O1)+H(K1))/H(M2)计算得到,其中H表示分潮振幅,K1,O1和M2表示各分潮。我国对于潮汐类型的规定:当F＜0.5时,为半日潮区;当0.5＜F≤2时,为混合半日潮区;当2＜F≤4时,为混合日潮区,当F＞4 时,为日潮区。由表1 可得,除Keling,Kukup和Sibolga-B三个验潮站属于混合半日潮区外,其余10个验潮站属于半日潮区。

由卫星测高数据进行潮汐信息的反演,主要是对卫星测高观测数据进行除海洋潮汐以外的各项改正。采用上述卫星数据主要是对干对流层改正、湿对流层改正、电离层改正、逆气压改正、海况改正和平均海平面基准改正六项参数不同的改正模型进行精度分析,此外还对测高数据进行了极潮、固体潮和参考框架改正。

图1 验潮站和卫星高度计的海面轨迹分布Fig.1 The distribution of the tidal stations and satellite along-track around the eastern Indian Ocean

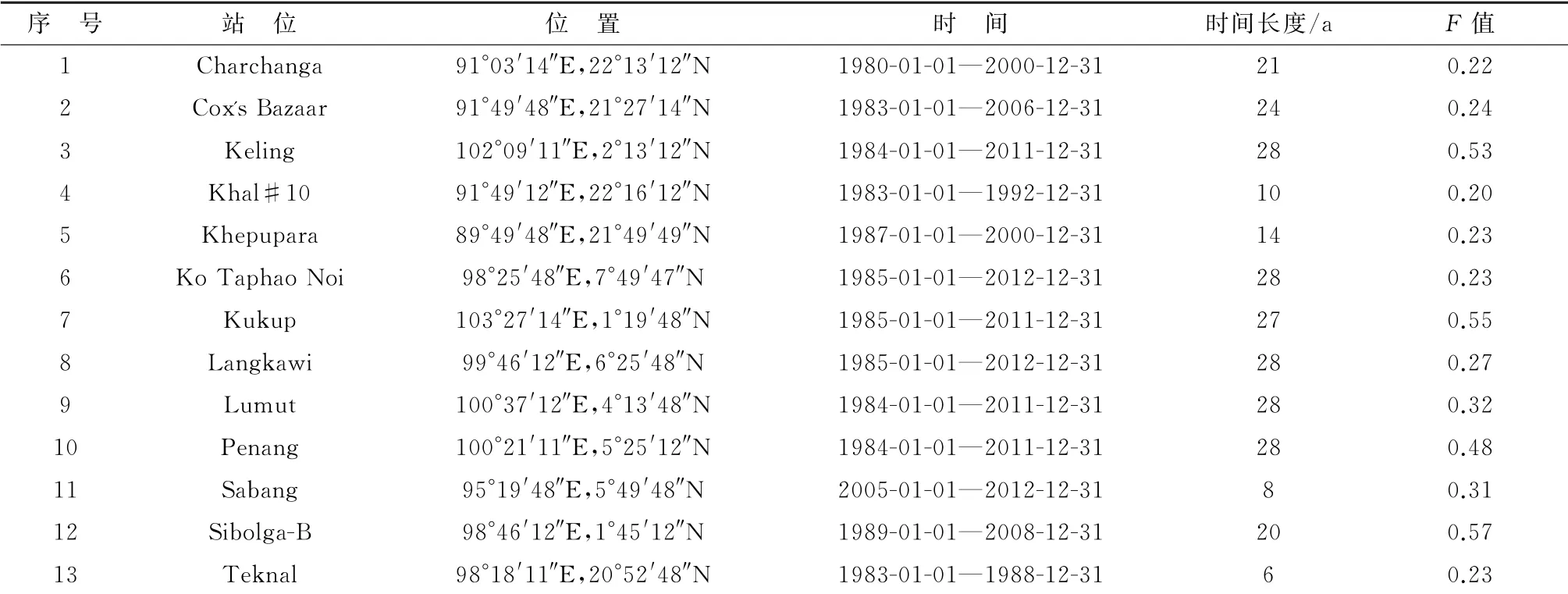
表1 验潮站的具体信息Table 1 The information of the tidal stations around the eastern Indian Ocean

1.2 卫星测高数据

本文研究范围为(88°～103°E,2°～22°N),图1中红线表示T/P高度计在本文研究区域的轨迹,采用的卫星高度计数据主要是执行精密重复轨道任务的TOPEX/Poseidon(T/P),Jason-1,Jason-2和Jason-3近24 a 的测高数据,对应的时间和周期见表2。

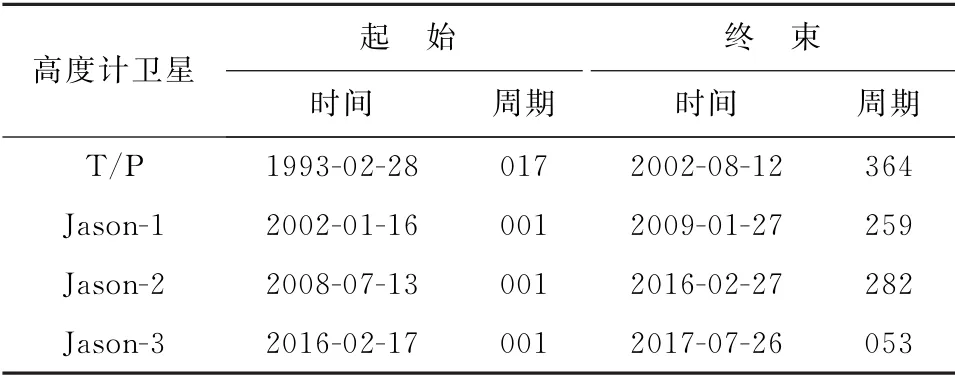
表2 采用的卫星高度计数据Table 2 Satellite altimetry data used in this study

1.3 潮汐模型

目前常用的潮汐模型大致分为2类:1)大洋潮汐的经验模型,主要通过卫星高度计等常规观测数据提取出潮汐信号,如CSR 模型,GOT 模型和DTU10模型等;2)大洋潮汐同化模型,基于潮波动力方程,采用各种同化方法,利用潮汐实测资料来提高潮汐模拟结果的准确度,从而获得全球大洋潮汐更准确的分布,如TPXO 系列模型[5]、FES系列模型等。

选取了国际上常用的6种全球潮汐模型:DTU10,EOT11a,FES2014,GOT4.8,OSU12和TPXO8,其主要参数和构建方法见表3。

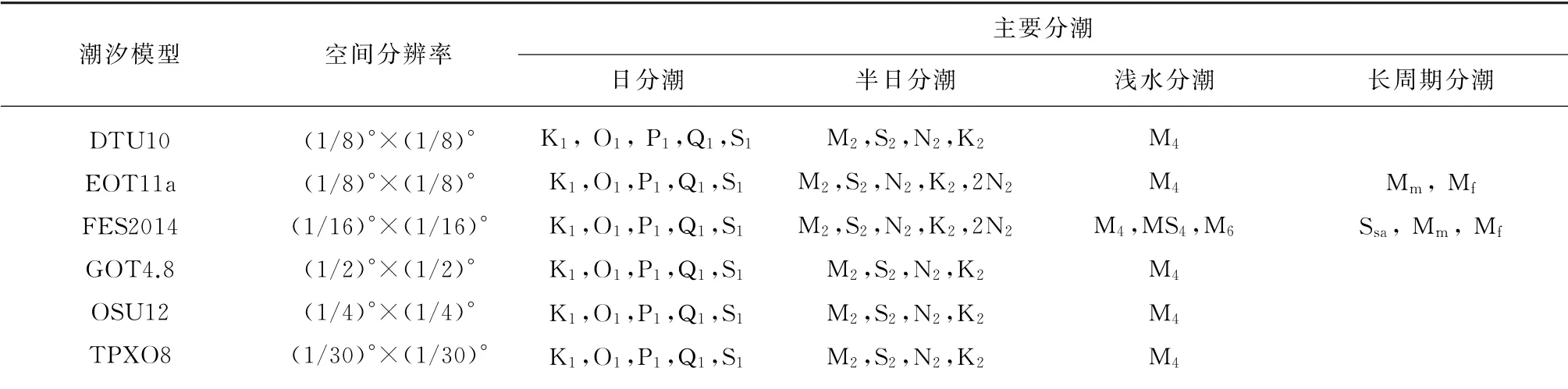
表3 六种潮汐模型的主要参数和构建方法[6]Table 3 Main parameters and construction methods for six tide models[6]

2 计算原理与评定方法

2.1 调和分析原理

实测潮汐信号可表示为平均海面、潮高和扰动因素的组合[7-9]:

式中:h0为分析期间的平均海面;t为潮位观测时间;f和μ为分潮的交点因子改正参数;δi为第i个分潮的角速率;M表示分潮总个数;χ为平衡潮分潮的初相角;x(t)为非天文潮位,具有随机的特性,在物理学上称为噪音;H为分潮的平均振幅;g为区时专用迟角;H和g称为分潮的调和常数[7-9]。

2.2 深度基准面计算

我国自1956年起,海道测量规范将深度基准面统一于理论最低潮面[8],理论最低潮面采用13个分潮组合潮高的极值,13个分潮中包含8个天文潮(Q1,O1,P1,K1,N2,M2,S2和K2),3个浅水分潮(M4,MS4和M6)以及2个长周期分潮(Sa,Ssa)。

目前深度基准值L的计算通常采用13个分潮取最小值,其计算公式:

式中:Lmajor为8个天文分潮叠加计算的可能出现的最低水位与平均海面的偏差;Lshallow为浅水分潮改正;Llong为长周期分潮改正。计算公式分别为

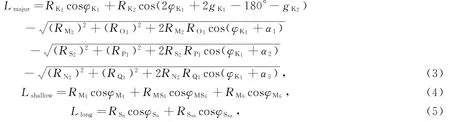
式中:α1=gK1+gO1-gM2;α2=gK1+gP1-gS2;α3=gK1+gQ1-gN2;R=fH,H,g,f为下标所对应的各分潮的调和常数和节点因数;φK1为分潮K1的相角,变化范围为0°～360°。

2.3 精度评定

1)分潮

由于多数全球潮汐模型仅提供了8个主要分潮的调和常数,因此,本文针对Q1,O1,P1,K1,N2,M2,S2,K2八个主要分潮进行精度评估,采用单分潮综合预报中误差(Root Mean Square,RMS)和多分潮综合预报误差(Root-Sum Square,RSS)评估潮汐调和常数的精度,定义公式为

精度评价指标主要由验潮站实测结果与全球潮汐模型构建的深度基准面模型值之间的最大值、最小值、平均值和中误差(σ),σ的公式如式(8)所示:

式中:N为验潮站的个数,LM,LT分别表示模型的深度基准面模型结果与验潮站的深度基准值。

3 结果分析

3.1 全球潮汐模型的精度评估

3.1.1 与卫星测高结果的对比

对卫星测高数据反演的潮高时间序列,根据式(1)进行调和分析,得到卫星测高沿迹点处8个主要分潮的调和常数。利用二次多项式插值方法提取出潮汐模型在卫星测高沿迹点处对应分潮的调和常数,根据式(6)和(7),对比卫星测高反演结果与潮汐模型结果,结果如表4所示。

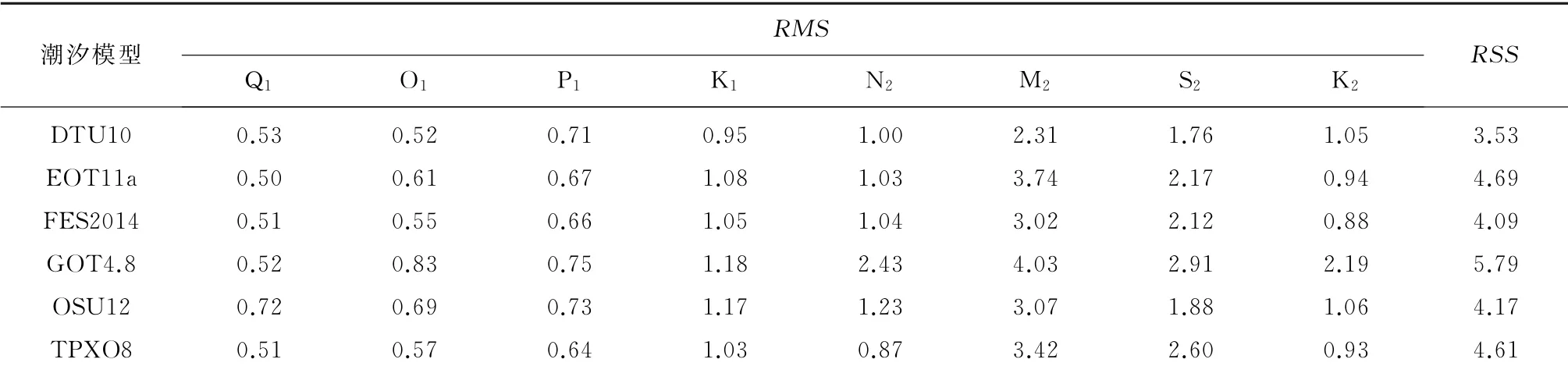
表4 卫星测高数据与潮汐模型在各分潮处RMS 和RSS 统计(cm)Table 4 RMS and RSS errors between the satellite altimetry data and the tide models(cm)

由表4可以看出,除M2分潮外,其余分潮的RMS值为0.50～2.91 cm,且6个模型之间的差异在毫米级;受M2分潮振幅较大的影响,其RMS值相对较大,为2.31～4.03 cm,其中DTU10精度最高。由各模型RSS结果可以看出,DTU10模型的精度较好,RSS值为3.53 cm,其次是FES2014模型,RSS值为4.09 cm;精度表现较差的是GOT4.8模型,其RSS值为5.79 cm。

无论是经验模型还是同化模型,与卫星测高反演结果对比,均具有较高的精度。这主要是因为在模型构建过程中两种模型均不同程度的采用了卫星测高反演结果,因此,采用卫星测高结果进行潮汐模型的精度评估可以看作为一种内符合精度的分析,为进一步分析潮汐模型在研究海域的精度情况,应采用验潮站实测结果进行精度评估。

3.1.2 与验潮站实测结果的比较

考虑到全球潮汐模型在近岸的影响因素,认为位于半封闭海域内的验潮站属于近海海域,将13个验潮站分成开阔海域与近海海域两类,开阔海域包括Khepupara,Ko Taphao Noi,Sabang和Teknaf四个验潮站,近海海域包括Charchanga,Cox's Bazaar,Keling,Khal#10,Kukup,Langkawi,Lumut,Penang和Sibolga-B九个验潮站。

对逐个验潮站长期潮位序列进行调和分析,得到主要分潮的调和常数。然后,采用二次多项式插值方法提取各个潮汐模型在验潮站点处分潮的调和常数,分别计算8个主要分潮模型结果与验潮站结果的RMS值,不同海域各分潮的对比结果如表5所示。

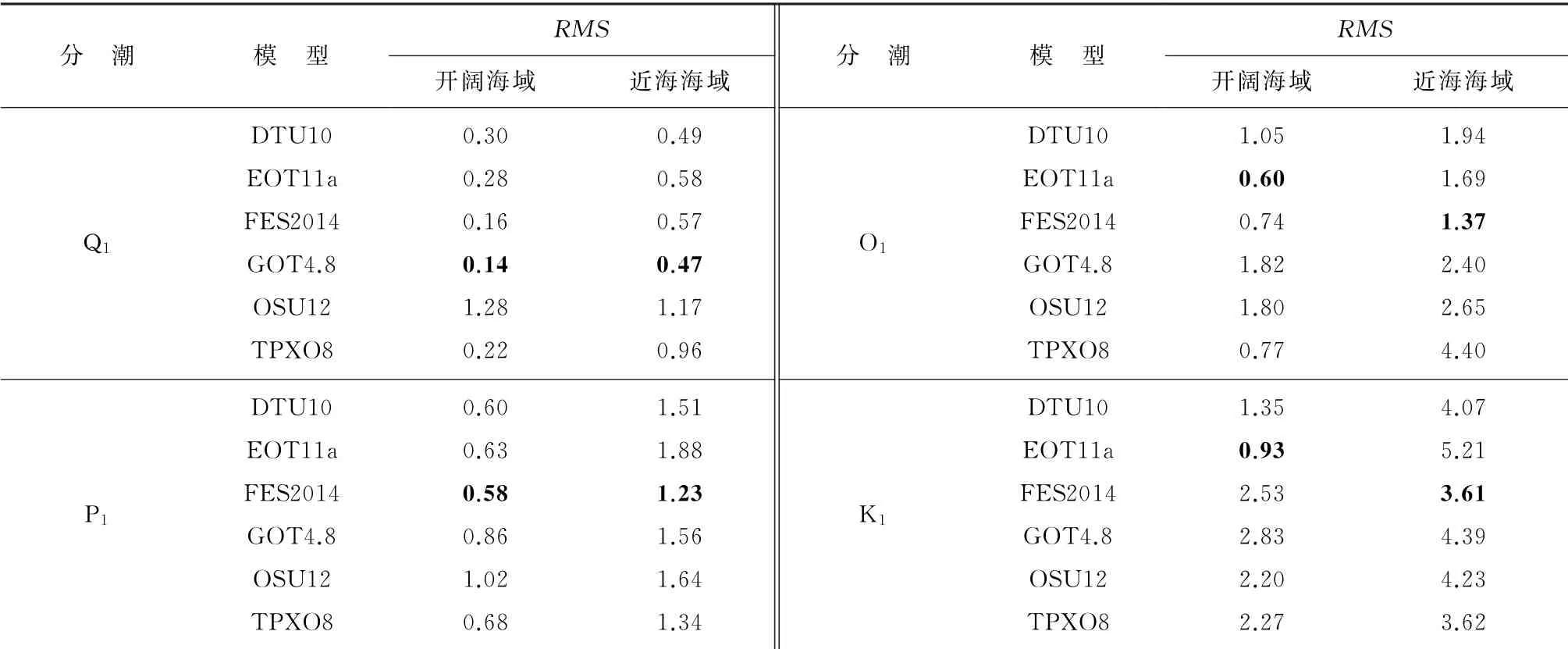
表5 潮汐模型在不同海域的各分潮RMS 的对比(cm)Table 5 Comparison of each tidal constituent RMS of tide models in different subareas(cm)

续表

由表5可知,在开阔海域,GOT4.8在Q1分潮精度最高为0.14 cm,FES2014在P1分潮处精度最高为0.58 cm,EOT11a模型在O1、K1分潮精度最高分别为0.60和0.93 cm,而N2,M2,S2,K2分潮均是DTU10模型精度最高;在近海海域,FES2014模型在O1,P1,K1,M2,S2,K2分潮处精度最高,GOT4.8在Q1分潮处精度最高为0.47 cm,OSU12在N2分潮处精度最高为4.39 cm。因此,DTU10和FES2014分别在开阔海域和近海海域的多数分潮处精度较高。为了评价多分潮综合预报误差,表6展示了潮汐模型在不同海域的8分潮的RSS的统计结果。

表6 潮汐模型在不同海域的RSS 的对比(cm)Table 6 Comparison of RSS of tide models in different subareas(cm)

由表6中可知,在开阔海域,DTU10模型的RSS值为11.98 cm,而GOT4.8模型可以达到35.10 cm,具有明显差异。在近海海域,FES2014模型的RSS值为24.04 cm,精度较差的为EOT11a模型,其RSS值为38.45 cm。因此,在深度基准面模型构建时,根据本文结果显示,在开阔海域建议采用DTU10模型;在近海海域建议采用FES2014模型。

3.2 最优深度基准面模型的构建

长周期分潮Sa和Ssa属于气象分潮,主要是由气象引起的,受周期性的风和气压的变化影响较大,因此,目前多数的全球潮汐模型并没有提供Sa和Ssa分潮调和常数。基于长周期分潮调和常数空间分布的较大尺度,本文使用卫星测高数据反演的结果构建了长周期分潮的经验模型。对于3个浅水分潮(M4,MS4和M6),本文计算了FES2014模型与卫星提取的浅水分潮改正量在13个验潮站处的差值,结果见表7,两者之间的差值最大值为1.75 cm,最小值为0.09 cm,这主要是浅水分潮振幅量级较小所致,鉴于两者差异较小,且为了构建空间分辨率一致的改正量模型,本文最终选取卫星测高结果构建的浅水改正量经验模型进行研究。

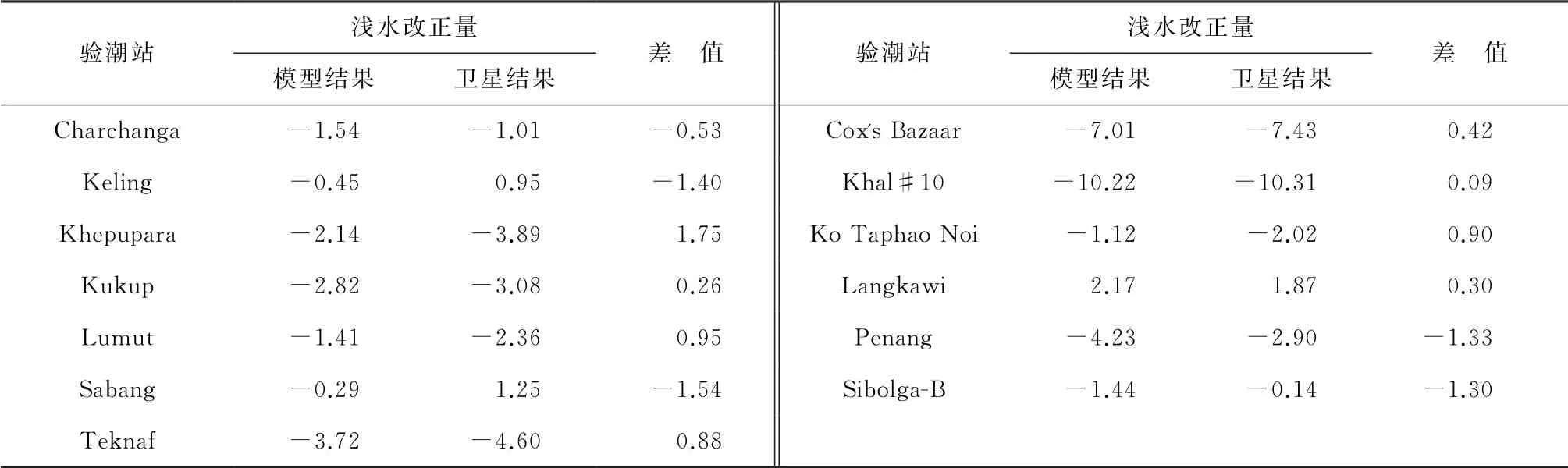
表7 模型结果与卫星测高结果在验潮站处浅水改正量的比较(cm)Table 7 Comparison between model results and satellite altimetry results in shallow water correction at tidal stations(cm)

在此基础上,构建了深度基准值确定过程中的长周期分潮改正量和浅水分潮改正量的经验模型,其数值在研究区域的空间分布如图2所示。

图2 浅水分潮改正量和长周期改正量在印度洋东部海域的分布Fig.2 The distribution of shallow water tide correction and long-period correction in the eastern Indian Ocean

根据式(2)所示,对Q1,O1,P1,K1,N2,M2,S2和K2八个天文分潮,本文提出一种最优组合模型,通过最优组合形成组合深度基准面模型以提高精度。

根据上述比较结果可知,DTU10和FES2014模型分别在开阔海域和近海海域表现为整体精度最优,但每个模型在各个分潮处RMS值表现各异,基于此,本文根据不同潮汐模型在各个分潮处的精度表现,试图提出一种组合模型进行深度基准面模型的构建。

在开阔海域,DTU10模型总体精度最优,但是,其Q1,O1,P1和K1分潮并不是精度最优的分潮,因此,构建的组合模型采用DTU10模型的N2,M2,S2和K2分潮,EOT11a模型的O1,K1分潮,GOT4.8的Q1分潮、FES2014的P1分潮及浅水分潮改正量和长周期分潮改正量进行组合,组合的模型记为DTU10-Z模型;在近海海域,FES2014模型精度最优,但是其Q1,N2分潮精度并不是最优的分潮,所以在近海海域,采用FES2014模型的O1,P1,K1,M2,S2,K2分潮、GOT4.8的Q1分潮、OSU12的N2分潮及浅水分潮改正量和长周期分潮改正量进行组合,组合的模型记为FES2014-Z模型。根据式(8),对组合模型构建的深度基准面模型进行精度评估,结果如表8所示。

表8 深度基准面模型值与验潮站结果的差值统计(cm)Table 8 Comparison between tide models and tide gauge station(cm)

如表7所示,在开阔海域,DTU10 模型的中误差为16.43 cm,组合模型DTU10-Z 模型的中误差为11.33 cm,DTU10-Z模型的精度由16.43 cm 提高到11.33 cm;在近海海域,FES2014模型的中误差为26.70 cm,组合模型FES2014-Z模型的中误差为20.95 cm,FES2014-Z模型的精度由26.70 cm 提高到20.95 cm。结果表明,组合模型的精度得到提高。

4 结 语

本文将印度洋东部海域(孟加拉湾、马六甲海峡和苏门答腊岛附近区域)内13个验潮站分成开阔海域与近海海域两类,评估了常用的6种全球潮汐模型精度。结果表明,多数潮汐模型与卫星测高反演结果精度相当;而与长期验潮站实测结果比较表明,其在开阔海域,DTU10模型8个主要分潮的RSS值为11.98 cm,表现为精度最优,在近海海域,FES2014模型RSS值为24.04 cm,精度最优,但在各分潮处RMS值精度差异,分别由DTU10和FES2014模型构建的深度基准面模型在研究海域的精度分别为16.43和26.70 cm。

本文根据潮汐模型在各分潮处的精度不同,首先构建了长周期分潮改正和浅水分潮改正的经验模型,在此基础上,提出一种组合模型进行精度最优的深度基准面模型构建。结果表明,组合模型在开阔海域和近海海域的精度分别提高至11.33和20.95 cm。对于进一步构建东印度洋海域无缝垂直基准面,由全球潮汐模型为基础构建的深度基准面模型可能无法满足精度的需求,建议在该海域构建区域潮汐模型,并结合优化的理论最低潮面算法,以及平均海平面模型、大地水准面模型,构建东印度洋海域的高精度、高分辨率的无缝垂直基准面模型。