非平稳需求下考虑碳配额的供应链选址-库存模型与算法研究
2020-05-28王旻轲张培文
吴 江,王旻轲,谭 涛,张培文
(西南财经大学统计学院,四川 成都 611130)
1 引言
近年来我国供应链行业发展迅速,但整体物流效率低、库存成本高、服务水平偏低等问题仍制约着供应链行业的发展。一方面,供应链基础设施的重复建设大幅增加了供应链网络的运营成本;另一方面,企业不断提升库存水平以应对客户需求的多样性和不确定性使得库存成本居高不下。随着国家节能减排战略的实施,低碳化经营已成为供应链企业绿色发展过程中一个不可忽视的因素之一。供应链企业的低碳形象可以增加顾客满意度与忠诚度,也可以在碳交易体系下通过交易剩余碳配额获得额外收益[1]。因此,面对变化多端的市场环境、绿色经济的迫切需求,高效、稳健的绿色供应链分销网络的选址-库存问题研究具有重要的现实意义与理论意义。
供应链选址-库存问题集成了企业战略层面的设施选址-分配决策和战术层面的库存控制,为多要素的集成问题。Daskin等[2]在传统无容量约束设施选址问题(UFLP)的基础上构建了包含选址、运输和库存等成本的非线性规划模型,通过拉格朗日松弛算法求解。Shen等[3]、Shu等[4]在Daskin等[2]的基础上提出不确定需求下的选址-库存模型,该模型参数为静态设定也未考虑决策变量的层级关系,通过列生成算法求解。Miranda和Garrido[5]研究了在平稳随机需求下考虑库存容量和订货量限制的供应链选址-库存问题,通过拉格朗日松弛和次梯度方法求解。Ozsen等[6]在Daskin等[2]和Shen等[3]的基础上构建了有容量约束和多源补货的选址-库存模型。Sourirajan等[7]研究了不确定需求下考虑库存补货提前期和安全库存的选址-库存问题,采用遗传算法求解构建的非线性整数规划模型。Park等[8]研究三级供应链选址-库存问题,认为零售商之间的需求相互独立。Shahabi等[9]在Park等[8]的模型基础上构建了零售商需求相关的选址-库存模型,通过渐近外逼算法求解。Puga ancrez[10]构建大规模的非线性选址-库存模型,提出迭代式的启发式算法来求解。Lim等[11]研究灵活供应链网络设计和库存分配问题,提出两种库存分配模式下的供应链网络最优设计方案。以上选址-库存模型大多采用(r,Q)库存策略,r为通过补货提前期内需求标准差计算的订货点,Q为在需求参数平稳假设下通过经济订货批量模型求得的最优订货量。
现实需求情景纷繁复杂,其不确定性需要多种方法构建的稳健供应链网络优化模型来应对。唐凯等[12]建立基于情景规划的随机多阶段选址-库存优化模型,通过拉格朗日松弛算法求解。黄松和杨超[13]在Daskin等[2]的基础上研究以期望销售收益最大化为目标函数的季节性商品的选址-库存模型,通过拉格朗日松弛算法求解。Amiri-Aref等[14]多源订货下的随机多阶段选址-库存混合整数规划模型,采用CPLEX优化器求解。马祖军和周愉峰[15]通过引入突发事件的发生概率构建了多情景、多阶段、需求随机下的血液战略储备库多目标选址-库存模型,设计了一种基于小生境技术的多目标NSGA-II 算法进行求解。Zahiri等[16]建立了模糊规划模型来研究医药品的供应链网络设计问题,并提出一种稳健优化方法解决参数的不确定性。以上文献大多在目标函数中用情景出现概率对参数和变量加权,即采用情景建模来构建稳健供应链优化模型,但需求参数取值仍为静态参数,不能反映出现实生活中需求的不确定性。
在考虑碳排放的供应链管理研究方面,Hugo和Pistikopoulos[17]构造了包含供应链运营成本和生命周期评估(Life Cycle Assessment)指标的混合整数规划模型,研究表明显著降低供应链运营成本不会增加对环境的负面影响。Chaabane等[18]研究了包含碳交易与供应链运营成本的混合整数规划模型,可平衡供应链运营成本和对环境的影响。Diabat和Simchi-Levi[1]提出了包含碳排放量约束的选址-库存混合整数规划模型,在不超过碳排放限额下设计并运营供应链网络。Sundarakani等[19]研究了四级供应链上各节点的碳排放类型以及各节点间碳排放的传递,为供应链的碳排放控制研究提供了依据。Wang Fan等[20]将分销中心环保投资决策变量加入供应链设计研究中,构建了包含供应链总成本和碳排放的双目标混合整数规划模型,但模型未引入碳配额参数。Elhedhli和Merrich[21]在供应链网络设计中考虑了碳排放成本,通过凹函数拟合碳排放与车辆重量的关系,利用拉格朗日松弛算法将问题分解为设施选址问题和凹背包问题。唐金环等[22]研究了包含碳配额差值和选址-路径-库存运作成本的多目标非线性整数规划模型,通过BFA-PSO组合优化算法求解。Alhaj等[23]构建了包含碳排放成本的最小化供应链选址-库存运营成本的混合整数规划模型。以上对低碳绿色供应链设计的研究大多构建最小化供应链成本和碳排放成本的双目标优化模型,并假设降低供应链成本会增加碳排放量。综上所述,现有文献对不确定性需求下低碳绿色供应链选址-库存问题的研究主要存在以下的不足:(1)虽然考虑了战略和战术层面的联合决策可以得到整体最优,但在模型构建上忽视了战略层面的选址-分配决策和战术层面的库存控制在决策层级性和作用时间跨度上的差异。(2)通常采用(r,Q)库存策略,并假设需求分布的参数为常数,缺乏研究非平稳需求下的选址-库存问题。(3)在低碳绿色供应链网络优化研究中,未见文献通过考虑碳交易背景将经济成本和环境影响的多目标问题构建为收益最大化模型。(4)在算法设计中较少考虑现实中企业可能的决策行为,没有研究选址导向和需求导向下的决策流程对决策结果的影响。
本文的创新点主要表现在:供应链企业在多期和多需求情境下,考虑碳配额、碳排放成本、多源补货、库存补充提前期和容量限制,采取(t,s,S)库存策略的三级供应链选址-库存问题,构建两阶段随机优化模型最大化企业供应链网络运营的期望收益,包括销售产品利润和交易碳配额差值的收益。针对本问题的NP-hard,本文设计三步骤分层级启发式算法,以选址导向或需求导向序贯求解为起始,对供应链企业在非平稳需求下的战略和战术层面决策问题进行求解。
2 问题描述与研究假设
2.1 问题描述
本文研究三级供应链分销网络选址-库存问题,网络节点如图1所示,产品由供应源(如:供货商)向分销中心(DC)供货,再由分销中心向下游需求点(如:零售商)派送以满足需求点不确定的市场需求。因战略决策为长期决策,备选分销中心的选址和与上下游节点的供货分配决策在第一阶段制定后将保持不变,而战术层面的库存控制,如:库存水平、订货和物流量决策需在每个计划期内制定以应对未知需求情景。综合考虑供应链运营利润与低碳合规收益,本研究最终给出最优的选址-库存策略以最大化供应链企业的期望收益。

图1 供应链网络结构
2.2 符号说明
I:供应源i集合,i∈I;
J:分销中心j集合,j∈J;
K:需求点k集合,k∈K;
T:计划期t集合,t∈T;
Ω:需求情景ξ集合,ξ∈Ω;
Xj:0-1变量,表明是否在备选地j开设分销中心;
Wij:0-1变量,表明供应源i和分销中心j是否存在供货关系;
Yjk:0-1变量,表明分销中心j和需求点k是否存在供货分配关系;

的现有库存;

的库存水平;
Ojt(ξ):0-1变量,表明需求情景ξ下第t期内分销中心j是否订货;
Qjt(ξ):需求情景ξ下第t期内分销中心j的订货量;
Lijt(ξ):需求情景ξ下第t期内供应源i向分销中心j的供货量;


2.3 研究假设
(1)需求点k在计划期t的总需求次数服从泊松分布Akt~P(λkt),单次需求数量服从正态分布Bkt~N(μkt,σkt),需求点之间、计划周期之间的需求相互独立。
(2)采用库存策略为(t,s,S),库存盘点在每个计划周期t末进行,若分销中心的库存水平小于等于s,分销中心即多源补货,总订货量为S-s。
(3)分销中心的库存补充提前期为L,分销中心在第t期末的订货量将在第t+L+1期初到货。
(4)分销中心在第t期内未能满足的需求将全部积压并形成缺货成本,积压的需求在第t+1期首先满足。
(5)供应链网络运营的碳排放成本包括分销中心开设碳排放成本和运输碳排放成本。
3 模型构建
3.1 库存策略参数表达式

(1)
(2)
根据Porteus[24]的调整报童模型,分销中心j在计划期t的S和s可构建为如下形式:
(3)
∀j,t
(4)

式(3)和式(4)右端第二项与变量Yjk存在非线性关系,通过采用Amiri-Aref等[14]提出的近似方法可得S和s的近似表达式:
(5)
∀j,t
(6)

3.2 考虑碳配额差值的随机两阶段选址-库存优化模型
针对现实生活中市场需求非平稳的情况,供应链企业收益包括销售产品的利润以及交易多余碳配额的收益,成本包括开设分销中心的固定成本、库存成本、缺货成本、采购成本、运输成本、以及开设分销中心、日常运营和运输产生的碳排放成本,本文提出的随机需求情景下两阶段选址-库存优化模型如下:
MaxR
(7)
s.t.Wij≤Xji∈I,j∈J
(8)
Yjk≤Xjj∈J,k∈K
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
Ojt(ξ)≤Xjj∈J,t∈T
(20)
Qjt(ξ)≤M·Ojt(ξ)j∈J,t∈T
(21)
(22)
Lijt(ξ)≤ψi·Wijj∈J,t∈T
(23)
Xj,Wij,Yjk,Ojt(ξ)∈{0,1}i∈I,j∈J,k∈K,t∈T
(24)
(25)


未满足供货流量只存在于有配送关系的供应链节点之间。式(20,21)表示只有开设的分销中心才能订货。式(22,23)表示分销中心可多源订货,订货量不能超过供应源的供货能力ψi。式(24,25)分别表示二分决策变量和非负连续决策变量的取值范围。
4 三步骤分层级启发式算法
本文研究大系统NP-hard问题,我们设计了三步骤分层级启发式算法进行大范围局部搜索,具有避免陷入局部最优的特点,同时结合MIP优化器的求解能力。步骤一:将3.2节的两阶段选址-库存优化模型分为战略决策子问题和战术决策子问题,按一定顺序求解子问题得到初始解。步骤二:将初始解输入模拟退火算法,寻找近似最优解。步骤三:模拟退火算法寻优达设定标准后运用GUROBI优化器的分支定界法逼近最优解。
4.1 序贯求解子问题
为保证序贯求解子问题得到的最终解在两阶段选址-库存优化模型中同样可行,可作为算法步骤二的初始解,以下所有子问题的约束条件同3.2节的模型,见式(8-25)。
4.1.1 选址导向的序贯求解
以选址为导向的企业更关注开设分销中心的固定成本、碳排放成本和建立物流配送渠道成本。因此,在选址导向的求解过程中首先最小化选址-分配产生的成本,目标函数为:
MinF(X,W,Y)=∑j∈J(fj+φεj)Xj+∑i∈I∑j∈JgijWij+∑j∈J∑k∈KljkYjk
(26)
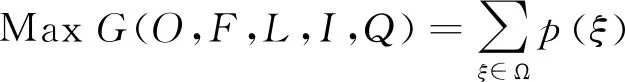
(27)
4.1.2需求导向的序贯求解

4.2 模拟退火算法
模拟退火算法能随机搜索当前解的邻域,在局部搜索的过程中以一定概率接受较差的解,从而可以跳出局部最优解,最终达到全局最优解[25]。本文的模拟退火算法如下:
(1)设定初始解:将步骤一中选址导向或需求导向的解作为模拟退火初始解X0。记Xbest=X0,X=X0,当前解的目标函数值为R(X0)。
(2)搜索邻域:在模拟退火的迭代中,根据4.3节的步骤产生邻域解Xnew。
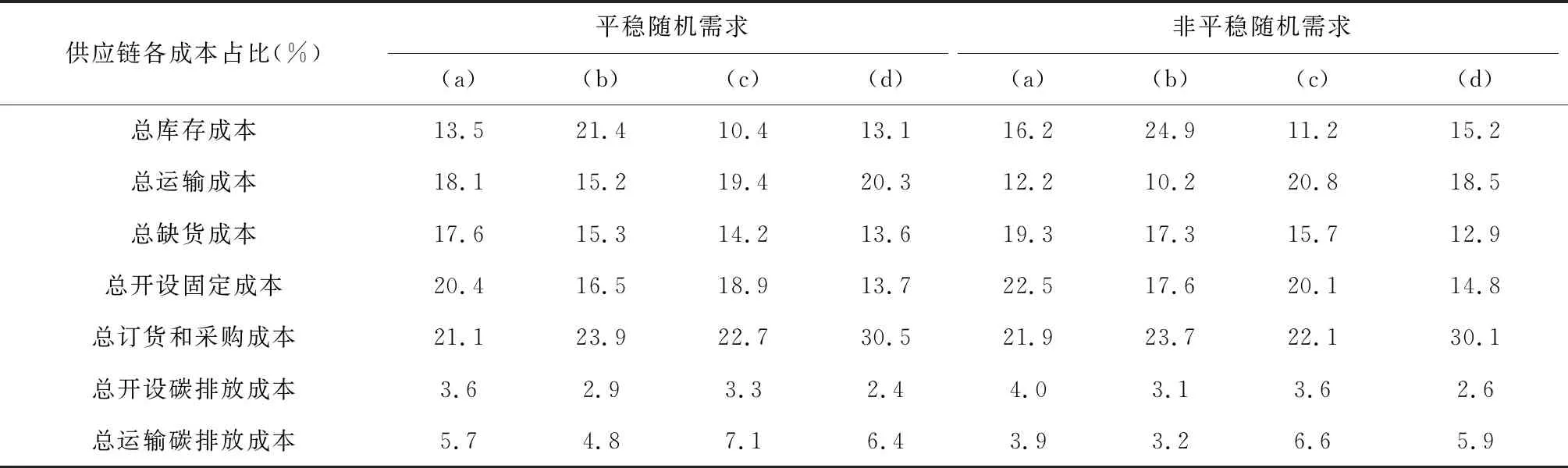
(3)随机选优:记ΔR=R(Xnew)-R(X),当前温度为T。如果Δ(R)≥0,记X=Xnew,Xbest=Xnew。如果Δ(R)<0,且U(0,1) (4)退火过程:当前温度T下的迭代次数如果没超过最大迭代次数MaxIter,回到第(2)步;如果超过MaxIter,降温到T=T×Cooling,Cooling为冷却速率。 (5)模拟退火终止:当T降低到终止温度时,停止模拟退火过程;否则回到第(2)步。 (6)后模拟退火(算法步骤三):将模拟退火算法得到的近似解作为初始解,利用GUROBI优化器的分支定界法逼近最优解。若GUROBI优化器在有限时间得到最优解,即为全局最优解;否则,通过设定求解时间限制参数TimeLimit终止求解,得到近似最优解。 在产生邻域解的过程中,将随机改变部分或所有决策变量取值。在改变部分决策变量的过程中,保持选址-分配决策变量不变,仅改变库存控制决策变量。在改变所有决策变量的过程中,先改变选址-分配决策变量,再改变库存控制决策变量。 4.3.1 选址-分配决策变量改变方法 4.3.2 库存控制决策变量改变方法 步骤1:记开设的分销中心的集合为openDC。计算每个开设的分销中心的未满足供货量和能满足供货量: (28) (29) 步骤2:开设的分销中心的现有库存和库存水平可计算为: (30) (31) 步骤4:随机选一个分销中心j∈orderDC,记其订货量Qjt(ξ)为Qorder。 步骤5:选取离该分销中心最近且SCi>0的供应源i。 步骤6:该供应源向该分销中心的供货量计算为:Lijt(ξ)=min{Qjt(ξ),SCi}。若Qorder>SCi,更新该分销中心的剩余订货量为Qorder=Qorder-Lijt(ξ),更新该供应源供货能力SCi为0,回到步骤5;若Qorder≤SCi,更新该供应源的供货能力为SCi=SCi-Lijt(ξ),并将该分销中心从orderDC移除。 步骤7:当orderDC为空,说明所有分销中心的订货量被满足,更新供应源-分销中心供货关系决策Wij,并进入步骤8;否则回到步骤4。 选取国内某供应链管理、商品批发零售企业为研究对象,对该企业在三个区域不同规模的供应链网络系统进行分析,网络节点数、节 点间距离,以及产品售价、缺货成本、库存成本等供应链运营成本见表1。 该企业以月度为基本计划周期,本文研究的计划周期为12个月。根据该企业面对的市场需求实际情况,将需求分为平稳随机需求和非平稳随机需 表1 供应链基本参数 求两种类型,假定有6和12个需求情景,需求概率分布参数取值列于表2。通过Monte Carlo模拟可得出需求情景ξ下周期t内需求点k的需求量χkt(ξ)。根据De Wolf等[26]构建厂房的材料和施工的隐含碳指标0.8-1.2吨CO2e/平方米,该企业5000m2到6700m2规模的分销中心的开设固定碳排放量εj服从[6000,8000]吨CO2e区间的均匀分布;根据Reich-Weiser等[27],运输碳排放系数e被估计服从[0.0006,0.0008]吨CO2e/吨-千米区间的均匀分布;根据Arikan等[28],商品在分销中心库存调配碳排放量θjk服从[0.005,0.008]吨CO2e/吨区间的均匀分布。碳价格φ为欧盟碳排放交易系统(EUETS)2018年碳价格10欧元/吨(折合75元/吨),供应链网络碳配额Φcap为150000吨。 表2 需求的概率分布参数 5.2.1 三步骤分层级启发式算法有效性分析 建立6个供应链网络规模,每个规模产生6个随机需求算例。首先运用GUROBI 8.0优化器根据3.2节的优化模型求解所有算例,求解时间限制参数TimeLimit设为3小时,优化差距参数MIPGap设为5%。然后用本文提出的三步骤分层级启发式算法求解所有算例,步骤一用GUROBI8.0求解子问题得初始解,步骤二用Python编程实现模拟退火算法,步骤三用GUROBI8.0求解3.2节的混合整数规划逼近最优解。 GUROBI优化器和三步骤启发式算法的平均求解能力和平均求解时间如表3所示,GUROBI分支定界法的优化差距为最优上界(UB)与有效下界(LB)的差值,并最终表示为有效下界的百分比形式,即(UB-LB)/LB×100%。三步骤启发式算法目标函数值提升比例为(Z-LB)/LB×100%,Z为三步骤启发式算法的最优解目标函数值。从不同规模的求解结果来看,(1)GUROBI的分支定界法在求解小规模算例时能在较短的时间内得到最优解,但随着算例规模的变大,分支定界算法的优化差距逐渐变大,最大达到12.87%。本文提出的三步骤启发式算法在各网络规模的求解中都不差于分支定界算法,平均优化提升比例为2.84%。(2)在计算时间方面,GUROBI的分支定界法在求解小规模算例时,计算速度略好于三步骤启发式算法,因为三步骤启发式算法中的模拟退火过程将尽可能的搜索解空间得到近似最优解直到设定最终温度。(3)通过对比不同规模的求解结果可以看出,需求情景数Ω|对GUROBI优化差距影响最大,因为需求情景数的增加使得问题的决策变量和约束条件都成倍增加,极大增加了问题的规模。 表3 算法求解有效性 5.2.2 序贯求解模式决策制定差异性分析 选址导向序贯求解和需求导向序贯求解在数值算例中计算出的平均供应链各成本的占比如表4所示。(1)在平稳随机需求下,相较于需求导向序贯求解方式,选址导向序贯求解方式的总开设固定成本和总开设碳排放成本占比较低分别为17.4%和3.1%,但总库存成本、总运输成本和总缺货成本占比较高分别为16.2%、19.4%和17.8%。(2)需求导向序贯求解方式会大幅增加总开设固定成本和总开设碳排放成本占比分别为34.8%、6.1%,降低总库存成本、总运输成本和总缺货成本占比分别为11.5%、15.3%和7.4%。(3)在非平稳随机需求下,选址导向和需求导向的成本占比差异仍然与平稳随机需求下的结果一致。以上结果说明两种子问题序贯求解模式在决策制定上存在不同侧重点,当碳排放监管政策着重于降低分销机构设立所产生的碳排放时,或企业拟建分销中心的监管区域的厂房建设碳税较高时,企业倾向于选择选址导向序贯求解来降低相应的成本,若运输碳排放碳税较高时,企业倾向于选择需求导向求解方式。 表4 不同序贯求解模式下供应链各成本占比 5.2.3 各求解方法下的供应链总成本分析 相同的供应链网络规模和参数设置下,不同求解方法计算出的总成本和各成本占比情况如图2所示。(1)无论在平稳还是非平稳随机需求下,三步骤分层级启发式算法得到的决策产生最少的成本,进一步说明三步骤分层级启发式算法在决策制定上的有效性,而仅仅序贯求解战略和战术层面子问题只能产生次优解。(2)需求导向的序贯求解比选址导向的序贯求解产生较少的成本,说明本文研究的供应链企业可认为是需求导向的。(3)相较于平稳随机需求,非平稳随机需求下的供应链运营会产生更多的成本,主要表现为开设分销中心固定成本、库存成本以及缺货成本的增加。可见,供应链企业在决策制定时应意识到战略决策和战术层面决策存在的内在联系,若单一考虑一个层次的决策问题只能得到次优结果,并增大运营成本。 图2 不同求解方式下供应链各成本占比 5.2.4 选址-库存决策敏感性分析 由开设分销中心固定成本、开设碳排放量、单位库存成本和单位缺货成本组成的四种成本结构如表5所示。各供应链网络规模在平稳和非平稳随机需求下与在不同成本结构下的平均开设分销中心数量如表6所示。(1)当开设固定成本和开设碳排放较高时,如(a)和(c)成本结构下,相较于(b)和(d)的低开设固定成本和低开设碳排放,供应链网络将少开设最高两个分销中心以降低开设分销中心带来的高成本。(2)当库存成本和缺货成本较高时,如(a)和(b)成本结构下,相较于(c)和(d)的低库存成本和低缺货成本,供应链网络倾向于增加开设一个分销中心以改善分销中心不足难以满足需求的情况。(3)需求的不确定程度会影响分销中心的开设数量,在同样的供应链网络规模和成本结构下,非平稳随机需求时的分销中心开设数量会比平稳随机需求的分销中心开设数量多一到两个,以弥补需求不确定性导致服务水平的降低。 各供应链网络规模在平稳和非平稳随机需求下和在不同成本结构下的平均供应链各成本占比如表7所示。(1)总库存成本占比随单位库存成本的降 表5 供应链成本结构 表6 不同供应链网络规模、需求类型、成本结构下的分销中心开设数量 表7 不同需求类型、成本结构下的供应链成本占比 低而减少,随开设分销中心固定成本的降低而增加。例如,当单位库存成本从(a)成本结构降低到(c)成本结构时,平稳随机需求下总库存成本占比从13.5%降低至10.4%。当开设固定成本/开设碳排放从(a)成本结构降低到为(b)成本结构时,平稳随机需求下总库存成本占比从13.5%增加到21.4%。(2)随着分销中心开设固定成本的降低,总运输成本和总缺货成本的占比相应减少。例如,当开设固定成本/开设碳排放成本从(a)成本结构降低为(b)成本结构时,平稳随机需求下总运输成本占比从18.1%减少到15.2%,总缺货成本占比从17.6%减少到15.3%;类似的各成本占比关系也可见于非平稳随机需求。这主要是因为当分销中心的开设固定成本降低后,将会开设更多的分销中心,带来更多的总库存成本,进而总运输成本和总缺货成本相应减少。(3)从各成本占比可以看出,非平稳随机需求下总库存成本、总缺货成本占比都有所放大,这可理解为较难找到合适的订货量、期末库存量来满足不确定需求;非平稳随机需求下总开设固定成本普遍增大,是因为需要增加开设分销中心以应对更为波动的需求。 假设该企业碳配额在120000吨到260000吨之间变动,从而得到该区间内在非平稳需求下的碳配额差值与供应链运营总收益曲线,如图3所示。可以看出,随着碳配额的增加,(1)碳配额差值逐渐下降变负,表明碳配额的剩余逐渐增加;(2)随着碳配额剩余的增加,企业总收益呈线性上升趋势,因为碳价格和碳交易机制的引入,企业可以将多余的碳排放配额在碳交易市场中转化为企业的额外收益。可见,虽然碳配额会一定程度限制企业运营活动,但允许碳配额交易可使企业灵活选择运营决策,通过合理运营达到节能减排的同时又能通过碳交易保证企业的经济效益。但政策性碳配额不会无限度增加,因此采取何种碳配额和碳价格水平取决于排放达标目标与企业经济效益的平衡。 图3 基于碳配额的供应链运营总收益和碳配额差值敏感性分析 本文研究供应链企业在多期、多需求情境下,考虑碳配额、碳排放成本、多源补货、库存补充提前期和容量限制的三级供应链选址-库存问题。根据决策变量的层级性,构建了随机两阶段优化模型,最大化供应链网络的期望收益,包括销售产品的利润和交易碳配额差值的收益。采用(t,s,S)库存策略作为分销中心的库存控制策略,通过调整的报童模型和线性近似方法得到了最优库存参数s、S的表达式,并将其引入约束条件从而起到在模型中优化库存控制决策变量的目的。针对问题的NP-hard属性,本文设计了三步骤分层级启发式算法,算法包括子问题序贯求解、模拟退火随机寻优和分支定界法逼近最优解。最后对我国某供应链管理企业的分销网络结构和相关数据进行算例分析,验证了三步骤分层级启发式算法的有效性,研究了两种子问题序贯求解模式在决策制定上的差异性,得到了以下管理启示:供应链管理中的战略和战术层面联合决策存在必要性,分离战略、战术层面决策只能带来次优结果,且增大运营成本;当需求非平稳时,供应链网络倾向于增加开设分销中心以弥补需求不确定性导致服务水平的降低;当缺货成本较高时,供应链网络同样会增加开设分销中心以降低缺货产生的惩罚成本;碳配额交易政策鼓励企业通过合理运营达到节能减排,并因此获得额外收益,而采取何种碳配额和碳价格水平取决于排放达标目标与企业经济效益。 现有研究还可以进一步拓展,首先可以考虑企业的低碳行为对顾客忠诚度的影响,从而研究顾客的低碳偏好下的绿色供应链选址-库存问题。其次,绿色可持续供应链管理不仅仅体现在供应链设计和物流上的节能减排,还体现在构建逆向供应链对废旧物品的回收再制造方面,因此可以研究多渠道的闭环供应链分销网络设计问题。第三,本文给出了一种较优的启发式算法,但当算例规模较大,尤其当需求情景数量较大时,算法的运行时间还需进一步提升,更高效的算法还有待进一步研究。4.3 邻域解产生方法

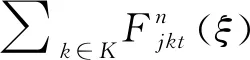



5 算例分析
5.1 参数取值
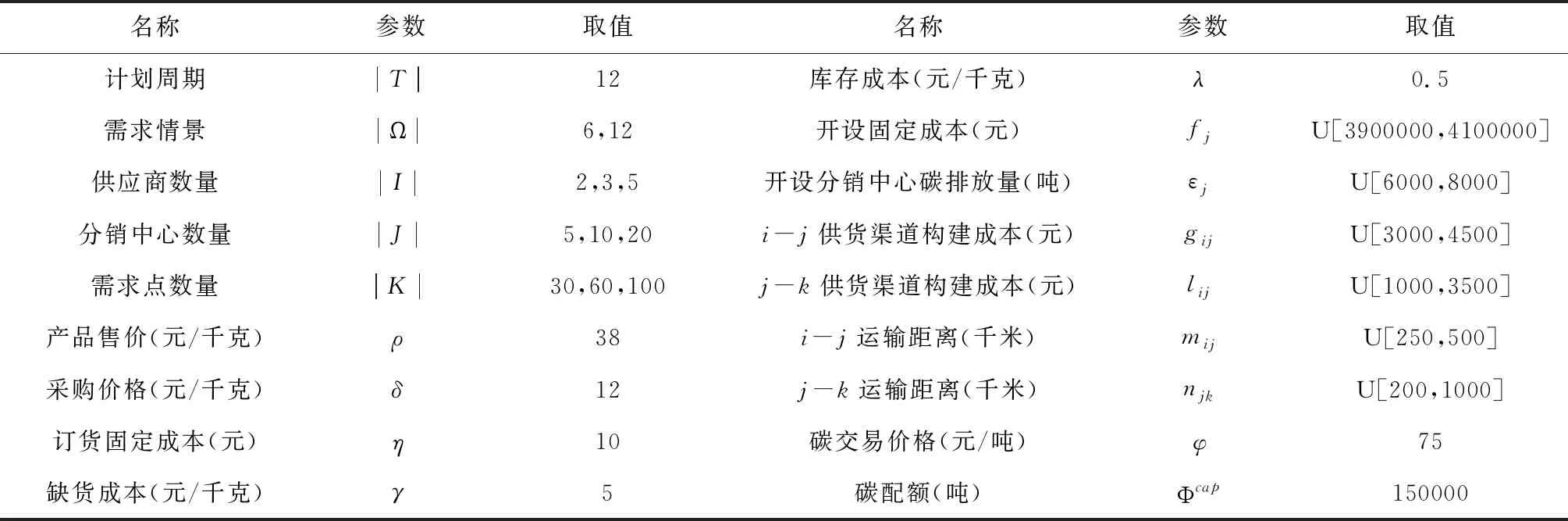

5.2 算例结果分析
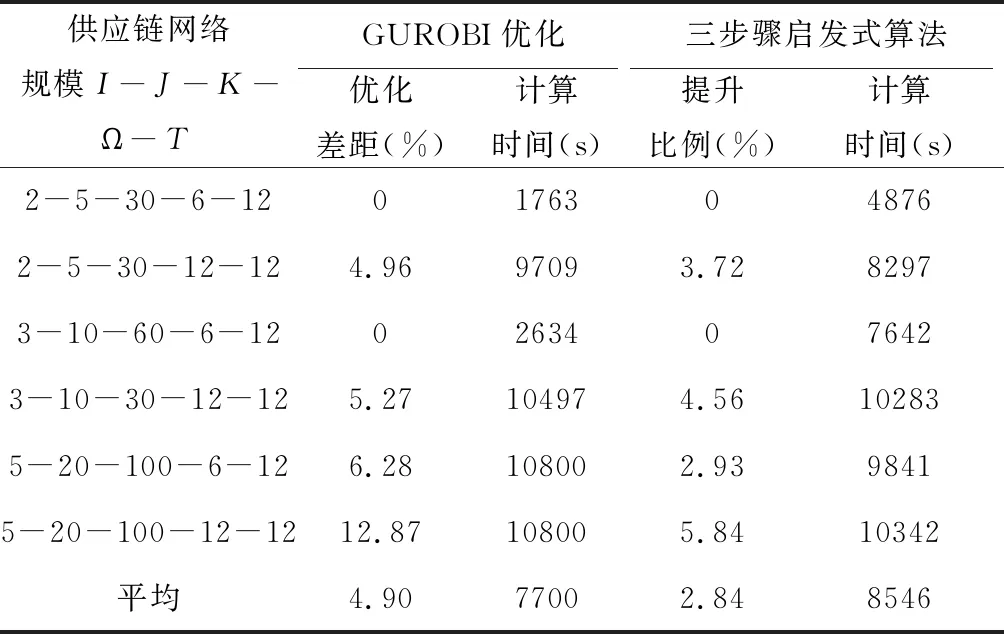
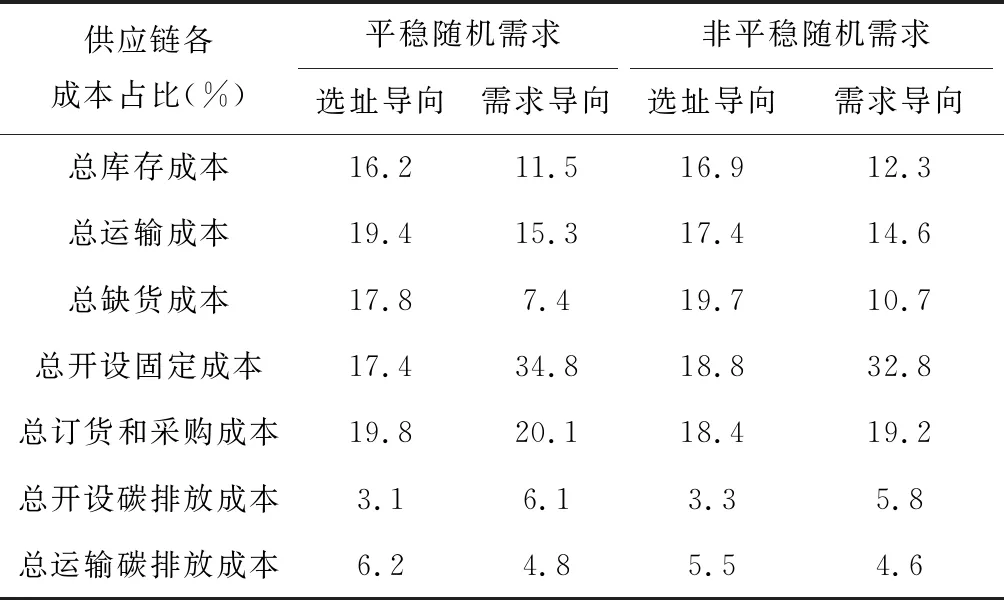




6 结语
