西安市用水需求量的多元线性回归预测

孙爱民

摘要：本文分析了西安市用水需求量的影响因素，选取了6个变量，收集了西安市2004年-2018年的全年用水总量和6个变量的数据建立了用水需求量与6个变量的多元线性回归模型。经检验，模型具有较高的拟合优度和整体显著性，但有个别变量的系数的线性显著性较低，为此运用SPSS建立了多元线性逐步回归模型。经检验，模型可用来对西安市的用水量进行模拟及预测。最后运用所建立的多元线性逐步回归模型对西安市2019-2022全年用水总量进行了预测。

Abstract： This paper analyzes the influencing factors of water demand in Xi'an， selects six variables， collects the data of total water consumption and six variables from 2004 to 2018 in Xi'an， and establishes a multiple linear regression model of water demand and six variables. After testing， the model has a high goodness of fit and overall significance， but the linear significance of coefficients with individual variables is low. Therefore， a multiple linear stepwise regression model is established by SPSS. After testing， the model can be used to simulate and predict the water consumption of Xi'an city. Finally， the multi linear step-by-step model is used to predict the total water consumption of Xi'an in 2019-2022.

关键词：用水需求量;多元线性回归;SPSS;预测

0  引言

西安市人均占有水資源仅相当于全国平均的11.6%，远低于国际平均水平，属于严重缺水型城市。随着国家中心城市的建设，人口的膨胀，经济的进一步增长，对水资源的需求量进一步加大，使得本就用水紧张的矛盾进一步加剧，严重影响了西安市建设国中心城市的进程。为了确保西安市的用水需求量，合理规划分配水资源，为用水量提供参考依据，分析用水需求量的主要影响因素，进而准确预测用水需求量具有重要的现实意义。

用水需求量的主要预测方法有多元线性回归模型和多元非线性回归模型、时间序列分析模型、灰色预测模型，神经网络模型等[1-6]。本文分析了西安市用水需求量的影响因素，选取了6个变量，收集了西安市2004年-2018年的全年用水总量和6个变量的数据建立了用水需求量与6个变量的多元线性回归模型，进而运用SPSS建立了多元线性逐步回归模型对西安市2019-2022全年用水总量进行预测。

1  多元线性回归模型

1.1 多元线性回归模型原理

1.2 多元线性回归模型的检验

多元线性回归模型的检验有：拟合优度检验、方程总体的显著性检验和变量的显著性检验。

1.2.1 拟合优度检验

拟合优度检验主要是检验方程的总体拟合情况，其原理是通过将总离差平方和分解为回归平方和加剩余平方和，进而用回归平方和与总离差平方和的比值即可决定系数的大小，来反映方程的总体拟合情况。

1.2.2 方程总体的显著性检验

方程总体的显著性检验即检验模型中被解释变量与解释变量之间的线性关系在总体上是否显著。

以上模型的参数的估计及检验可通过SPSS软件计算。

2  用水量的多元线性回归模型

2.1 变量的选取及数据获取

记西安市全年用水总量为Y，城市人口数量为X1，地区生产总值为X2，固定资产投资额为X3，生产运营用水量X4，居民家庭用水量X5，年末供水管道总长度X6。选取2004-2018年的相关数据，见表1，数据来源于《西安市统计年检》。

2.2 多元线性回归模型

分别作出全年用水总量与各影响变量的散点图，见图1。从图1可看出全年用水总量与各影响变量大致呈线性关系趋势，因此可建立全年用水总量与各影响变量的多元线性回归模型。运用SPSS进行计算，得模型回归方程为

2.2.1 拟合优度检验

由SPSS运算结果知模型的可决系数R2=0.988，调整的可决系数R2=0.980，方程的拟合优度非常高。

2.2.2 回归方程的显著性检验

由表2可知，F=114.232，给定显著性水平α=0.05，查表可得临界值F0.05（6，8）=3.58，F>F0.05（6，8），回归方程的总体线性关系显著。

2.2.3 回归方程的变量系数的显著性检验

SPSS返回的回归方程的变量系数的显著性t检验结果见表3。给定显著性水平α=0.05，查表可得临界值t0.025（8）=2.3060，由表3可知，t4>t0.025（8），其余的t统计量值小于临界值，因此，除过变量X4外，其余变量对Y的解释作用不显著，需要对自变量进行删减后，重新建立模型。

2.3 多元线性逐步回归模型

2.3.1 逐步回归方程的拟合优度检验

SPSS返回的可决系数R2=0.986，调整的可决系数R2=0.984，方程的拟合优度非常好。

2.3.2 逐步回歸方程总体的显著性检验

SPSS返回的逐步回归方程显著性F检验结果见表4。

由表4可知，F=435.057，给定显著性水平α=0.05，查表可得临界值F0.05（2，12）=3.89，F>F0.05（2，12），回归方程的总体线性关系显著。

2.3.3 逐步回归方程的变量系数的显著性检验

给定显著性水平α=0.05，查表可得临界值t0.025（12）=2.1788，检验统计量的值为t4=11.017，t5=8.101，t4>t0.025（12），t5>t0.025（12），因此变量X4，X5对Y的解释作用显著。

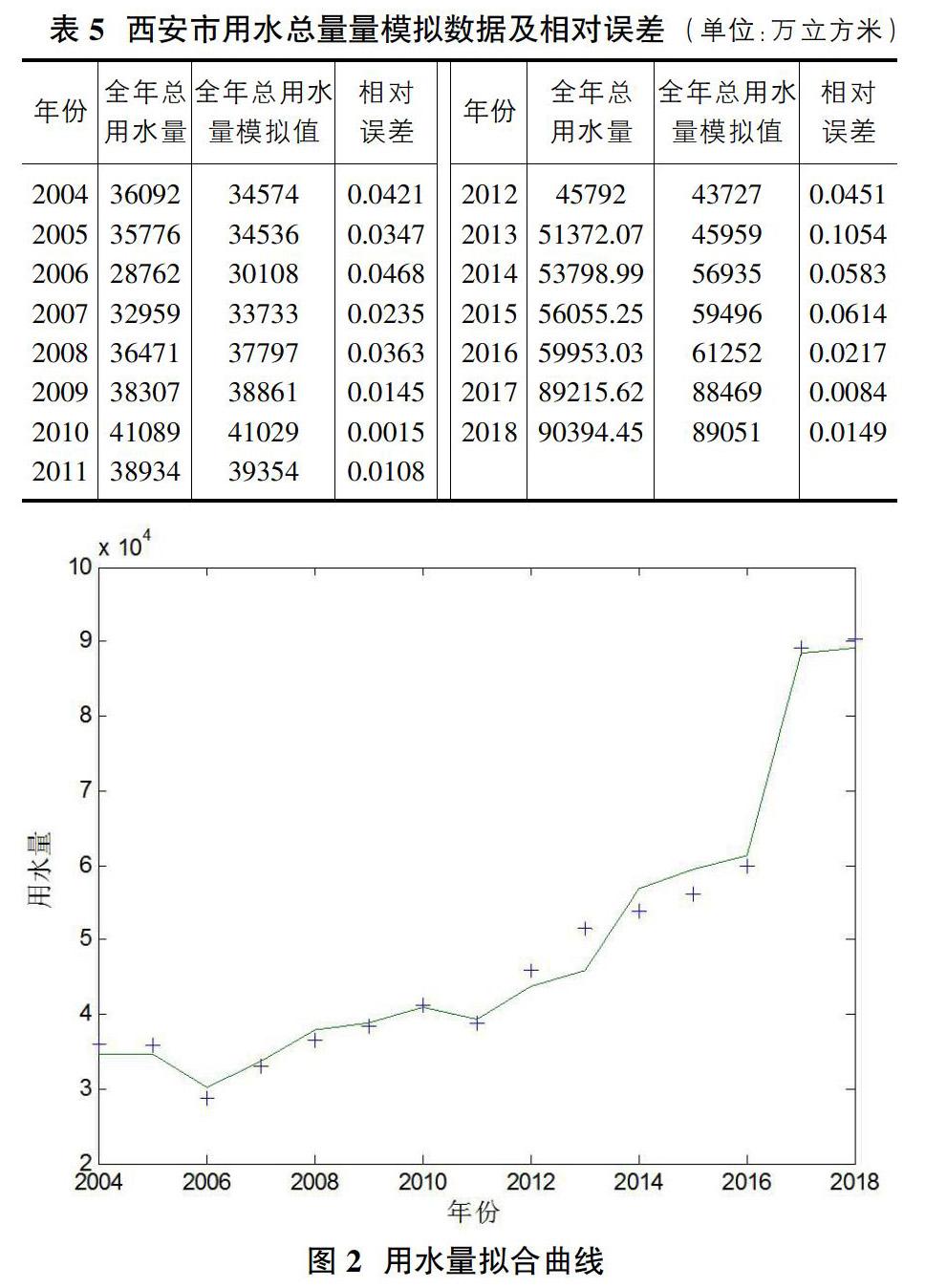
2.3.4 西安市2004年-2018年全年用水总量的模拟

逐步回归方程经过各项检验均符合要求，可用来对西安市的2004年-2018年全年用水总量进行模拟。模拟结果见表5，拟合曲线图见图2。由表5及图2可知模拟的效果非常好。

3  西安市2019-2022年全年用水量预测

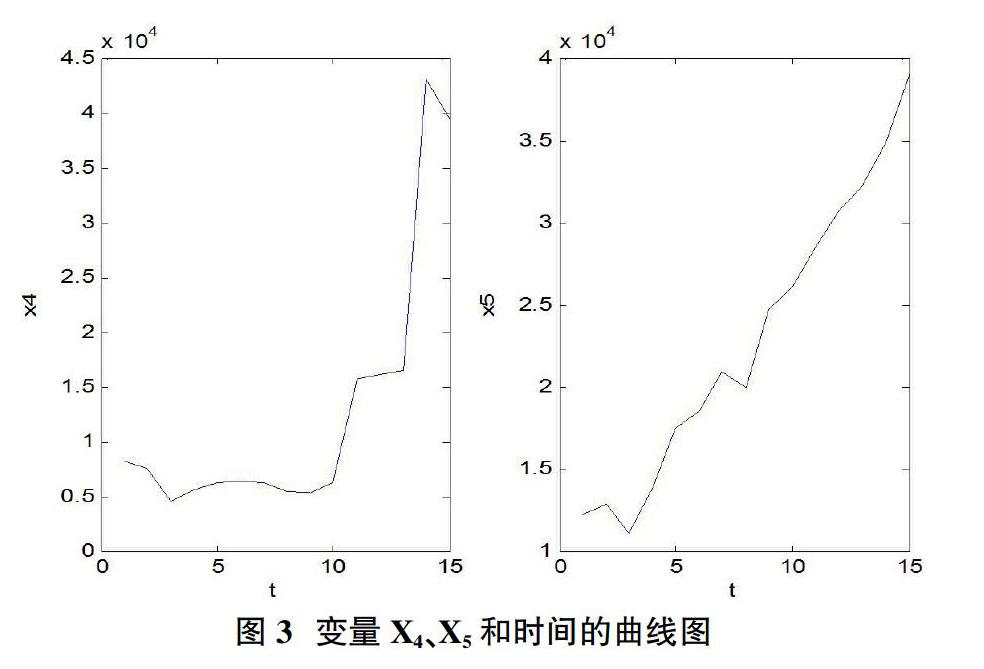
用逐步回归方程（2）来预测2019年-2022年的全年用水量需要知道变量X4和变量X5在2019年-2022的数据。为了得到2019年-2022年的变量X4和变量X5的数据，需要分别建立变量X4、X5和时间的拟合方程。

记2004年的时间t=1，则2004年-2018年对应t的值从t=1到t=15。以时间为横轴，表1中变量X4、X5的数据为纵轴，分别作出变量X4、X5和时间的曲线图，如图3所示。

分别计算（3）、（4）在t=16，t=17，t=18，t=19的值，得变量X4，X5在预测年份的值，进而由（1）式计算出全年用水量Y在预测年份的值，计算结果见表6。

由表6看出，2019-2022年西安市全年用水总量预测值依次为95940万立方米、106130万立方米、117080万立方米、128800万立方米。

4  结束语

本文通过构建多元线性逐步回归模型对西安市2019年-2022年全年的用水总量进行了预测。根据预测结果，到2022年西安市的全年用水总量将达到128800万立方米，为此西安市应进一步优化水资源配置，防止供水紧张，确保西安市经济社会发展的需要。

参考文献：

[1]张雄，党志良，张贤洪，马丁.城市用水量预测模型综合研究[J].水资源与水工程学报，2005，16（4）：24-28.

[2]周鹏飞，卢泽雨.基于SPSS多元线性回归模型在城市用水量的预测[J].水利科技与经济，2018，24（5）：6-10.

[3]刘治学，张鑫，王颖华.包头市市区居民生活用水量预测分析[J].水资源与水工程学报，2012，23（5）：67-70.

[4]谢敏萍，王志良，王得利.基于灰关联分析的多元线性回归模型在城市年需水量预测中的应用[J].华北水利水电学院学报，2007，28（6）：10-12.

[5]孙丽芹，常安定，位龙虎，等.基于GM（1，1）一逐步回归模型的用水量预测[J].统计与决策，2016（20）：95-97.

[6]黄胜.灰色系统与多元逐步回归耦合模型[J].节水灌溉，2007（5）：38-40.