基于风险度和灰色理论的电梯安全评价及应用

杜自豪，王 强，吴琳琳，朱 凯，徐晓萌，袁昌明

(中国计量大学质量与安全工程学院，杭州 310018)

近年来，随着高层建筑的增多，电梯的使用量及数量大大增加，截至2018年底，中国电梯的数量已达627.83万台[1]，电梯作为与人们日常生活关系密切的交通工具之一，其重要性不言而喻，电梯作为一种特种设备，其发生故障后造成的事故严重性较大，目前因电梯故障导致的事故伤亡案例不断发生，因此开展电梯的安全评价工作具有重要的意义。

目前对电梯的安全检查主要是定期的检验，传统的评价方法只能定性检测电梯系统的安全状况，对电梯部件的检测也只是给定一个标准判断是否合格，这对于电梯系统的具体好坏程度没有一个明确的指导，所以如何将定性的评价转化为定量的评价是目前电梯评价工作中的重点。Park等[2]通过检查电梯每个部件安全状况，来量化电梯的风险水平；丁思娴等[3]应用层次分析法(AHP)确定各个指标的权重，通过建立灰色关联矩阵，实现对电梯的评价；万林等[4]采用AHP-CRITIC综合法，得到指标的综合权重，结合模糊综合评价方法，实现对电梯的评价；陈兆芳等[5]引入信息熵来计算指标的权重系数，结合灰色关联法，实现对电梯的评价；张广明等[6]结合了模糊层次分析法和人工神经网络法，用于对电梯的风险评价；任馨[7]研究了人员风险伤害事件的发生概率以及后果严重程度，从而构建了一种电梯风险评价模型；李中兴等[8]将预先危险性分析法和故障类型和影响分析法相结合，实现对电梯的评价；庆光蔚等[9]将AHP和模糊综合安全评价法相结合，用于对电梯的风险评价。当前对电梯的评估方法中，部分采用层次分析法确定权重，但其包含了专家不可避免的主观意见，部分采用熵权法确定权重，其未考虑到被评估指标本身的重要程度；而当两者权重组合的时候，只是单纯相加；对电梯安全状况进行评价时，选取的评价方法未考虑到电梯的模糊性和不确定性，且缺乏对电梯安全状况的动态修正。

鉴于此，将电梯评价指标按照严重度和可能性等两方面进行详细划分；同时结合了AHP法和熵权法，从主观和客观两方面来确定权重，并且引入了距离函数法和最小相对信息熵原理确定出权重组合，改进了权重以减少确定权重时带来的误差，在运用灰色理论的基础上引入风险度理论对电梯的风险值进行修正，通过判断电梯系统的风险等级，更加准确地判断电梯所处的安全状态。

1 改进权重法

1.1 AHP

AHP是美国运筹学家莎蒂提出的一种多层次权重分析决策方法[10-11]。

基本步骤如下。

(1)构造判断矩阵。首先建立层次评价体系结构，将系统分为3个层次：目标层、准则层和指标层。

(2)构造判断矩阵。采用1～9级标度法来构造判断矩阵，对指标因子之间进行两两比较，构建出判断矩阵An=[aij]n×n，其中aij表示i元素和j元素的比较结果，n表示判断矩阵中指标个数。

(1)

(4)计算权重向量W′i：

(2)

(5)计算判断矩阵的最大特征根λmax：

(3)

式中：Ani表示判断矩阵An的第i个行向量；W′表示权重向量集合。

1.2 熵权法

熵权法通过指标所提供的信息量来计算指标权重，信息熵越小，其权重越大，信息熵越大，其权重越小[13]。

基本步骤如下。

(1)建立决策矩阵。假如有m个参与评价的对象，有n个评价指标，用xij表示第i个评价对象对第j个指标的评价值[14]，则构成的决策矩阵为X=(xij)m×n(i=1,2,…，m；j=1,2,…,n)。

(2)决策矩阵标准化：

(4)

式(4)中：fij表示第i个评价对象的第j个指标经标准化处理后的值，由其组成的标准化决策矩阵为f=(fij)m×n。

(3)计算第i个指标输出的熵Hi:

(5)

(4)计算第i个指标的权重W″i：

(6)

1.3 组合赋权

运用最小相对信息熵原理和距离函数法分别来计算AHP和熵权法的组合值，然后取两种组合值的平均值作为最终的权重。

令AHP确定的权重集合为W′i，熵权法确定的权重集合为W″i，(i=1,2,…,n)。

1.3.1 距离函数法

通过式(7)计算出分配系数α、β和组合后的权重值，其中Wai为距离函数法求得的权重组合。

(7)

1.3.2 最小相对信息熵原理

(8)

式(8)中：Wbi为最小相对信息熵原理求得的权重组合。

1.3.3 算术平均值

2 基于风险度和灰色理论的电梯评价模型

2.1 建立电梯风险度指标

将电梯按照严重度和可能性两方面进行详细的指标划分，如图1所示。

图1 电梯风险度指标

2.2 建立评价样本矩阵

设共有P位专家对电梯指标中的各因子进行打分，由其构成的评价样本矩阵为[15]

(9)

式(9)中:vij表示第j个专家对因子vi的打分结果。

2.3 确定评价灰类

采用专家打分法将电梯风险等级划分为4个等级，即评价灰类e为4个，分别是P1、P2、P3、P4，对应为差、中、良、优，对应分值为0～60、60～80、80～90、90～100，则白化权函数q为4个，建立基于中心点的三角白化权函数[16]，相应的白化权函数分别为f1(x)、f2(x)、f3(x)、f4(x)。其中：

(10)

(11)

(12)

(13)

2.4 划分评价等级

由评价灰类个数可知，将电梯系统风险评价等级分为4个等级，相对的评分标准及对策见表1。

2.5 计算灰色评价系数

2.6 计算灰色评价权向量

对于vi，指标层对应第e个评价灰类的评价权数为rije，即rije=xije/xij，记指标层对应各灰类的灰色评价权向量为rij，即rij=(rij1,rij2,…,rijq)。

2.7 计算灰色评价权矩阵

将系统中所有指标层对应各灰类的灰色评价权向量进行综合，可得到指标层灰色评价权矩阵Rs(s=1,2,…,n)。

(14)

表1 电梯系统风险评价等级标准及对策

2.8 准则层的综合评价

将指标层灰色评价权矩阵Rs与指标层权重Ws相结合获得一级评价结果，记为Ds，就有Ds=WsRs；由Ds可知准则层的灰色评价权矩阵R=(D1,D2,…,Ds)T，结合准则层权重W，可得二级评价结果，结果记为D，就有D=WR。

2.9 目标层的综合评价

根据划分的灰类分值，得到向量C=(C1,C2,…,Cg)，然后确定电梯事故严重度的综合评价值，记为Y，即Y=DCT，同理求出电梯事故可能性的综合评价值Y′。

2.10 风险修正

分别求出电梯事故严重度和可能性的综合评价值，通过电梯事故可能性的综合评价值来修正电梯的风险值，具体修正值见表2。

表2 电梯风险的修正值

图3 电梯事故严重度评价指标

2.11 计算电梯风险值

将电梯事故的严重度综合评价值与电梯事故的可能性综合评价值的修正值相结合来评价电梯的安全状况，即Q=Yf，根据划分的风险等级标准，从而可得到电梯系统的风险等级。

3 案例分析

下面针对某乘客电梯展开具体评价工作，该电梯已使用13 a，载荷1 000 kg，额定速度1.75 m/s，楼层为5层5站。从电梯事故可能性和严重度等2个方面建立电梯的评价指标体系，如图2、图3所示。

图2 电梯事故可能性评价指标

3.1 求权重

3.1.1 AHP求权重

建立评价指标集，根据上述的指标确定电梯系统的准则层指标集合，A=(A1,A2,A3,A4,A5,A6,A7,A8)，其中A1的指标层集合为(A11,A12,A13,A14,A15,A16,A17,A18)，Aij表示为准则层Ai的第j个指标层，同理可得其余指标层集合。

首先根据AHP求出各准则层和目标层的权重，以准则层为例做具体分析，根据公式求出W′1=(0.253 7,0.049 7,0.072 3,0.068 7,0.078 8,0.107 6,0.139 5,0.229 7)，检验判断矩阵的一致性，通过判断矩阵求得CI=0.044 0，并求出CR=0.031 2<0.1符合要求，同理可得其余权重。

3.1.2 熵权法求权重

邀请10名由电梯的研究专家、电梯使用者、电梯管理者、电梯开发商及电梯监管单位组成的专家组，按照指标1～9重要性程度的标准度，分别对构造的指标进行打分，以A11为例做具体分析，利用式(4)对各指标数据进行标准化处理，然后再用式(5)、式(6)计算各指标的熵及熵权，计算得出H1=0.994 1，W″1=0.036 8，同理可计算其余指标的权重。

3.1.3 组合赋权法求权重

通过式(7)可计算出距离函数法中组合系数α=0.62,β=0.38(因实际评价中AHP法考虑到指标的安全状况，故分配系数时令α为较大值)，通过式(8)计算的详细权重及通过取平均值后的权重组合最终值如表3所示。

表3 电梯的权重组合

3.2 计算灰色评价向量

5位专家对电梯风险打分值如表4所示；以A11为例具体分析，计算电梯系统的灰色评价系数和灰色评价向量，如表5所示。

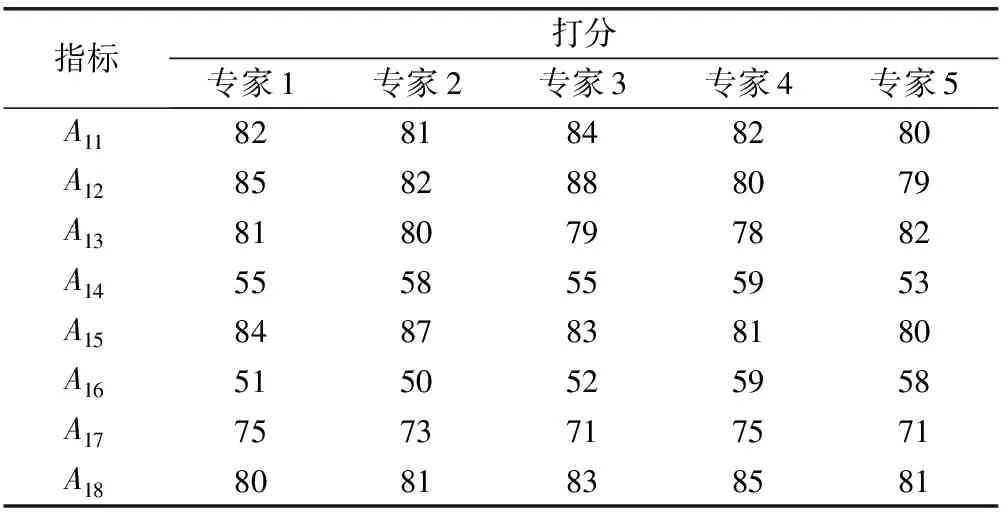
表4 电梯风险分值

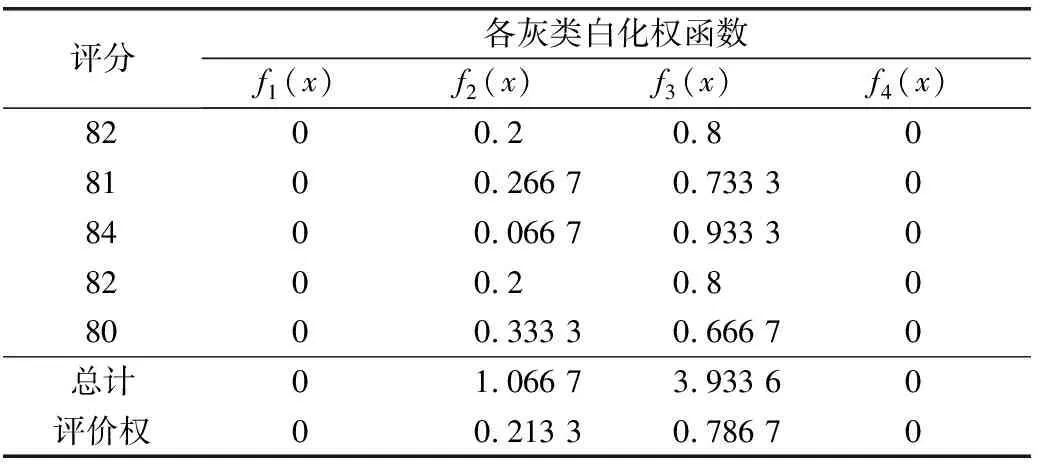
表5 A11灰色评价系数

可得A11灰色评价向量A11=(0,0.213 3,0.786 7,0)，同理可得其余灰色评价向量，分别为A12=(0,0.186 7,0.753 3,0.060 0)；A13=(0,0.333 3,0.666 7,0)；A14=(0.350 0,0.650 0,0,0)；A15=(0,0.160 0,0.800,0.040 0)；A16=(0.400 0,0.600 0,0,0)；A17=(0,0.800 0,0.200 0,0)；A18=(0,0.200 0,0.800 0,0)。

则A1的灰色评价矩阵为

(15)

同理可得其他灰色评价矩阵。

3.3 综合评价

计算电梯事故严重度评价向量：D1=W1×R1=(0.061 9,0.339 9,0.587 6,0.005 2)；D2=W2×R2=(0,0.335 4,0.664 5,0)；D3=W3×R3=(0.148 7,0.500 3,0.350 9,0)；D4=W4×R4=(0.410 1,0.589 9,0,0)；D5=W5×R5=(0.121 3,0.487 6,0.350 1,0.041)；D6=W6×R6=(0,0.620 0,0.380 0,0)；D7=W7×R7=(0.050 0,0.350 0,0.500 0,0.100 0)；D8=W8×R8=(0.200 0,0.500 0,0.300 0,0)。则：D=W×R=(0.215 7,0.071 1,0.091 9,0.069 2,0.069 5,0.086 0,0.183 8,0.212 8)×

同理可知，电梯事故可能性评价向量D′=W×R=(0.141 0,0.301 0,0.433 7,0.124 3)。

3.4 风险值修正

由于电梯事故可能性评价向量为D′=(0.141 0,0.301 0,0.433 7,0.124 3)，根据划分的灰类分可知C=(30,70,85,95)，可以确定电梯事故可能性评价值Y′，Y′=D×CT=73.973 0根据划分的风险修正值可知，修正系数f为0.9；电梯事故严重度目标层评价值Y=D×CT=72.136 7，则修正后的电梯风险值为Q=0.9×72.366 5=65.923，故电梯风险等级为II级，急需采取措施以降低乘用风险，通过建立对比试验可知，未建立风险度理论得到的电梯风险为58.732 1，仅考虑电梯部件因素而得到的电梯风险为72.136 7，修正后的电梯风险值处于两者之间，即58.732 1≤65.923≤72.136 7，经分析可知因未建立风险度理论时放大了“人、环境、管理”的影响因子，而仅考虑电梯部件因素时减小了“人、环境、管理”的影响因子，从而证明运用风险度理论修正法能准确反映电梯的安全状况，而且实际评估过程中发现电梯管理和维保未跟进到位，此评价结果与该电梯实际情况等相吻合。

4 结论

(1)采用主客观两种权重计算方法，保证了权重的准确性，同时又融入了最小相对信息熵原理和距离函数法来确定权重组合，减小确定权重组合时带来的误差。

(2)对电梯从严重度和可能性等两方面建立了多方位的评价模型，进行多层次的分析，引入了风险度理论对电梯的风险进行了修正，并进行了对比试验，综合考虑未建立风险度理论而得到的电梯风险和仅考虑电梯部件因素而得到的电梯风险之间的分值大小，从而证明风险度理论修正法能准确地反映出电梯的安全状况，以便及时做出相应的处理措施。