基于修正因子的雾天可变限速控制交通流模型

2020-05-25孙长乐高宏岩

科学技术与工程 2020年10期

孙长乐, 高宏岩

(山东科技大学电气与自动化工程学院，青岛 266590)

雾天天气加剧了高速公路系统的复杂性、不确定性和随机性，不仅降低了交通效率，而且加大了交通事故发生率[1-2]。由于高速公路主线可变限速控制通过对路段限速使得交通流更加均匀、稳定，进而改善交通安全[3-5]、缓解交通拥堵[6-8]，所以主线可变限速控制已经成为治理雾天高速公路交通问题的重要途径[9-13]。

中外专家对雾天高速公路可变限速控制问题进行深入研究，取得了许多重要成果，如基于K近邻算法预测实时速度与能见度的可变限速控制[14]，基于传感器技术的雾天自动报警系统[15]，基于交通数据信息融合的智能交通系统[16]，基于模糊聚类分析对雾天进行等级划分的可变限速控制[17]和基于道路状态的模糊可变限速控制[18]等。上述中外文献表明，雾天高速公路可变限速控制研究日趋成熟，正在逐步降低雾天天气对高速公路系统的影响。但现有研究成果中交通流模型很少考虑道路因素与雾天因素对于高速公路的实时影响，即交通流模型的在线自调整。

现首先基于Takagi-Sugeno(T-S)模型以雾天条件下高速公路曲面半径与实时能见度为输入变量，得到为输出变量的雾天修正因子，进而构建含有雾天修正因子与可变限速因素的交通流模型。本文提出的基于修正因子的雾天可变限速控制交通流模型，综合考虑道路因素与雾天因素对于高速公路可变限速控制的影响，以期提高雾天可变限速作用下交通流模型精度，在实际应用中具有一定的价值。

1 雾天可变限速控制下交通流模型

1.1 T-S模型理论

雾天可变限速控制作用下的高速公路是一个具有不确定性、复杂性、随机性等特点的非线性系统，而T-S模型是非线性复杂系统模糊建模的一种经典模糊动态模型，因此，采用T-S模型对高速公路系统建模。

对于T-S模型，假设xi(i=1，2，…,M)是第i个输入变量，其中M是输入变量的数量，Al(xi),l=1，2，…，L)是输入变量xi的模糊子集，其中L是模糊规则的数量。T-S模型中第l条模糊规则用以下IF-THEN形式表示：

(1)

假设μl(xi)是输入变量xi对应模糊子集Al(xi)的隶属度，μl是第l条模糊规则的真值，计算方式为

μl=min[μl(x1),μl(x2),μl(x3),…,μl(xM)]

(2)

或者

μl=μl(x1)μl(x2)…μl(xM)

(3)

T-S模型最终输出值可以用解析式(4)表示。

(4)

1.2 宏观交通流模型

雾天可变限速控制宏观交通流模型不仅考虑速度限制对于高速公路特性的影响，还将雾天天气对于高速公路特性的影响考虑在内，正常天气下的可变限速交通流模型难以适用，因此，采用T-S模型提出一种基于雾天修正因子的可变限速交通流模型。

高速公路能见度与曲面半径是雾天天气下影响高速公路运行的两大重要因素,因此将高速公路实时能见度与曲面半径分别作为T-S模型的输入变量,雾天修正因子cf为T-S模型的输出变量。因此，雾天修正因子可以通过T-S模型根据高速公路能见度与曲面半径在线实时调整，进而实现雾天可变限速交通流模型在线自调整。本文提出的雾天可变限速交通流模型如下。

(5)

qi(k)=ρi(k)vi(k)λi

(6)

vi(k+1)=[1-Bi(1-cf)][vi(k)+

(7)

V[ρi(k)]=vfbi(k){1-[ρi(k)/(ρjam{1+

Ci[1-bi(k)]}]}δ]m

(8)

式中：T为采样周期；λi是路段i的车道数；vi(k)、ρi(k)分别是路段i在k时刻的平均速度、平均密度；qi(k)是路段i在k时刻流量；ui(k)是即将进入路段i的入口匝道流量；vf、ρjam和Δi分别是自由流速度、阻塞密度和路段i长度，m、τ、γ、θ、δ、Ai、Bi和Ci是代表雾天可变限速作用下高速公路特性的常数变量；bi是路段i的限速比率；cf是雾天修正因子。

式(5)、式(7)表明相比于正常天气，雾天高速公路主流密度与速度会随着雾天修正因子的变化进行线性变化，式(8)表明可变限速作用下高速公路速度与密度关系的变化，其中自由流速度会变为限制速度，阻塞密度会随着限速比率的变化而进行线性变化。

1.3 雾天修正因子调整

将道路能见度与曲面半径作为T-S模型的输入变量，雾天修正因子作为T-S模型输出变量。假设k时刻的高速公路能见度与曲面半径为s(k)、c(k),A(s)、B(s)分别为输入变量s(k)、c(k)的模糊集合。根据专家知识，每个输入模糊集合都预先定义了两个模糊子集。输入模糊集合与输入变量的论域均为[-1,1]。

假设输入变量s(k)、c(k)的实际物理域分别为[s1,s2]、[c1,c2],通过平均值sm、cm与量化因子Ks、Kc对输入变量测量值进行论域归一化，归一化后论域均为[-1,1]。论域归一化过程如下：

sm=(s1+s2)/2,cm=(c1+c2)/2

(9)

Ks=1/(s2-sm),Kc=1/(c2-cm)

(10)

A(s)=Ks[s(k)-sm],A(c)=Kc[c(k)-cm]

(11)

归一化后的输入模糊集合隶属度函数如图1所示。

T-S模型模糊规则中输入变量组合共有4种，如表1所示。

图1 输入模糊集合隶属度函数图

表1 模糊规则中输入变量组合

T-S模型中第l条模糊规则用以下IF-THEN形式表示：

(12)

(13)

本文提出的T-S模型有4条模糊规则，每条模糊规则结论部有3个需要优化调整的参数，所以T-S模型共有12个需要优化调整的参数。包含m、τ、γ、θ、δ、Ai、Bi和Ci高速公路特性参数在内，本文提出的雾天可变限速交通流模型共有20个参数需要优化调整。因此，雾天可变限速交通流建模问题就转化为参数寻优问题。

1.4 灰狼优化算法

灰狼优化算法是一种基于迭代的群体智能进化类算法，算法结构简单、参数较少、易于实现,因此采用灰狼优化算法对交通流模型参数进行优化调整。算法基本原理：灰狼群体中的每一匹狼都代表一组潜在解，狼群中适应度值最佳的三匹狼分别命名为α狼、β狼和δ狼，其余狼群均称为ω狼。在狼群迭代过程中根据适应度函数计算每一匹狼的适应度值，基于适应度值选出狼群中的α狼、β狼和δ狼，根据α狼、β狼和δ狼的位置调整ω狼的位置，逐渐向最优值靠近，直至达到控制要求或最大迭代次数，α狼的位置便是最优解。灰狼种群位置调整过程可以用如下解析式表示。

Di=|CiXp(t)-Xi(t)|

(14)

Xi(t+1)=Xi(t)-AiDi

(15)

Ai=2ar1-a

(16)

Ci=2r2

(17)

式中：Di是灰狼i与猎物(最优解)的距离,Xi是灰狼i的位置，Ai和Ci是常量系数，a是收敛因子，r1和r2是0～1的随机数。

由于Xp(最优解)未知，灰狼优化算法中种群个体的位置调整受α狼、β狼和δ狼的领导进行位置调整，所以实际中种群中个体位置更新公式如下：

Dα=|C1Xα(t)-Xi(t)|

(18)

Dβ=|C2Xβ(t)-Xi(t)|

(19)

Dδ=|C3Xδ(t)-Xi(t)|

(20)

X1=Xα(t)-A1Dα

(21)

X2=Xβ(t)-A2Dβ

(22)

X3=Xδ(t)-A3Dδ

(23)

Xi(t+1)=(X1+X2+X3)/3

(24)

式中：Dα、Dβ和Dδ分别代表第t次迭代时灰狼i与α狼、β狼和δ狼的距离，Xα、Xβ和Xδ分别代表α狼、β狼和δ狼的位置，Xi(t)是第t次迭代时灰狼i的位置。

适应度函数的选取直接影响到灰狼优化算法对模型参数优化的快速性与最优性。交通流量、密度和速度是交通流模型的三大重要因素，采用速度与密度的平均绝对百分比误差为适应度函数，而速度与密度之积等于流量，所以本文提出的适应度函数充分表达了交通流模型的特性，满足交通流模型参数优化要求。适应度函数表示为

(25)

式(25)中：ρo(k)代表k时刻交通流模型密度；ρi(k)代表k时刻实际交通密度；vo(k)代表k时刻交通流模型速度；vi(k)代表k时刻实际交通速度。

交通流模型参数优化程序框图如图2所示，灰狼优化算法参数配置如表2所示。

图2 灰狼优化算法程序框图

表2 灰狼优化算法参数配置

2 仿真实验

2.1 仿真设置

为验证文中所提交通流模型的有效性，首先使用VISSIM软件获取雾天高速公路可变限速控制下的交通数据，然后将数据导入MATLAB进行交通流仿真。以一段两车道并带有一个入口匝道的高速公路为仿真对象，将高速公路均匀划分为5段，每个路段长度均为640 m，入口匝道长度为400 m。高速公路仿真如图3所示。

路段3为建模路段，仿真时间从1:00 am—23:40 pm，仿真步长T=10 s，路段2流量和入口匝道流量如图4所示。实验仿真环境设置：能见度为150 m，曲面半径为1 500 m，能见度与曲面半径的实际物理域分别为[100 m,200 m]、[500 m,1 500 m]，式(9)～式(11)中，sm=150,cm=1 000,Ks=0.02，Kc=0.002。

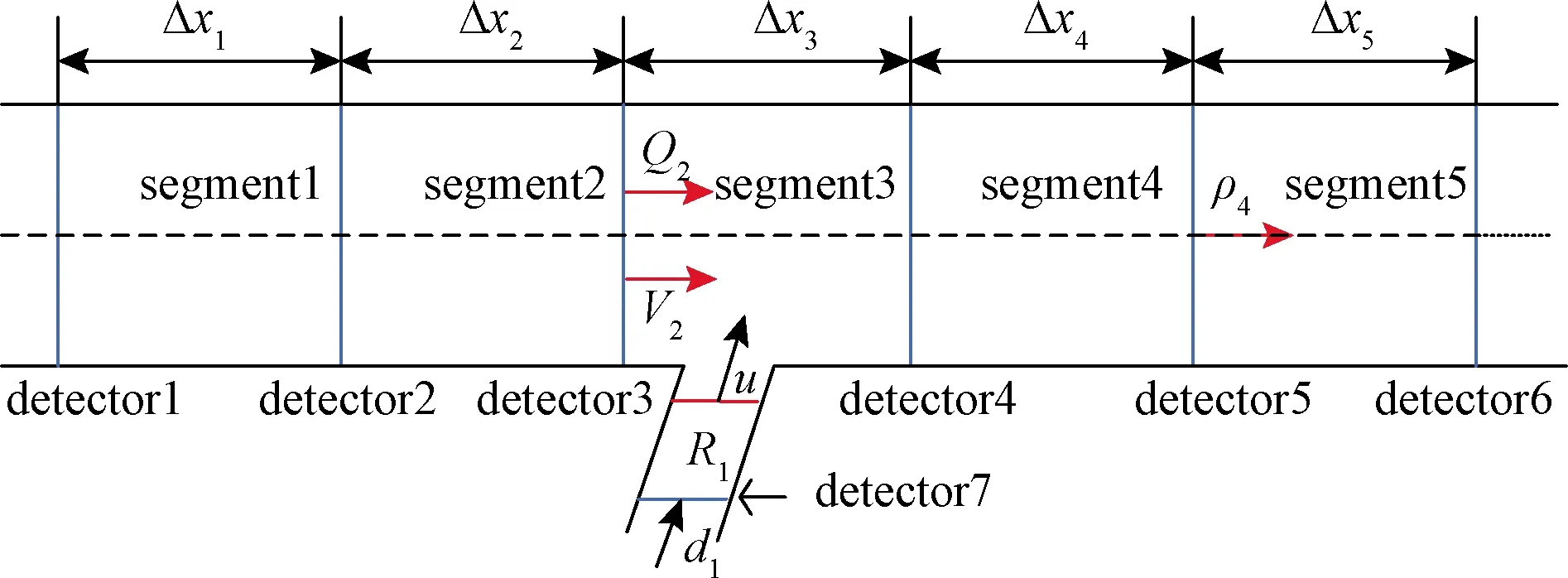
图3 仿真路段示意图

图4 交通数据图

2.2 仿真结果与分析

为验证本文提出交通流模型的有效性与可靠性，构建了雾天天气下高速公路在限速值85 km/h与75 km/h两种仿真场景，每个场景分别进行一般可变限速交通流模型与本文提出交通流模型的仿真对比。仿真对象为雾天可变限速作用下的同一路段，用速度与密度的平均绝对百分比误差评价模型的准确性，仿真结果如图5、图6所示。

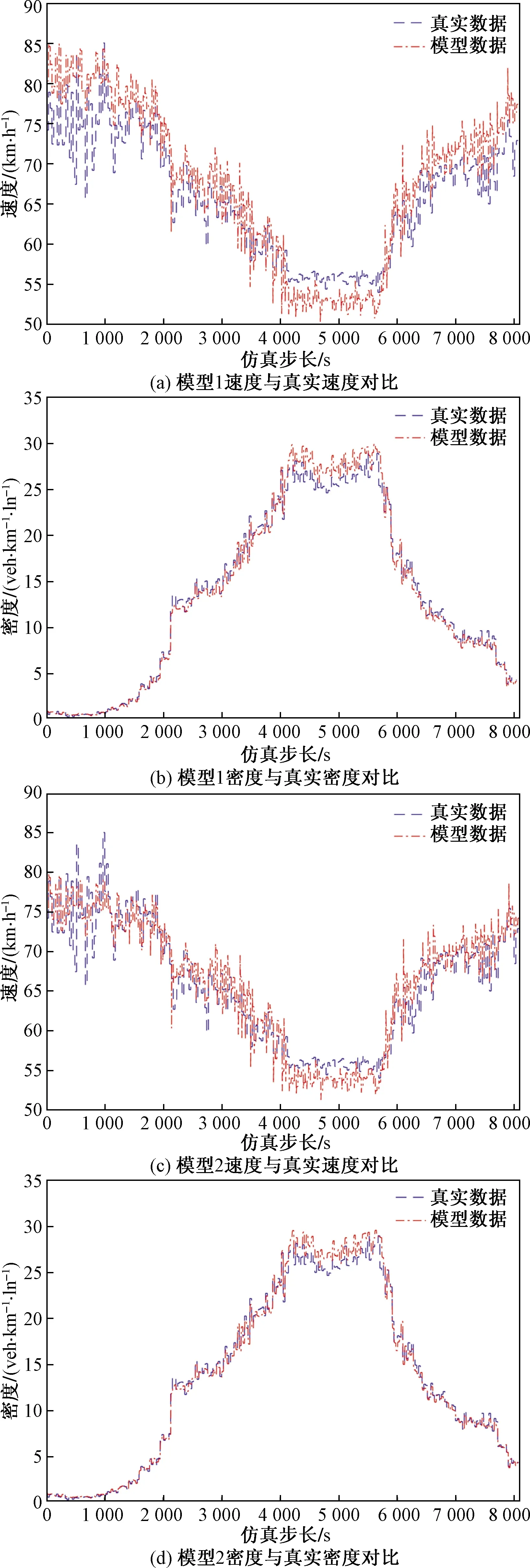
图5 场景1仿真效果对比图

图5为限速值为85 km/h场景的仿真结果，模型1为一般可变限速交通流模型，模型2为本文提出的交通流模型。由图5分析可得，一般可变限速模型的速度与密度的绝对百分比误差分别为4.72%和6.21%，本文提出交通流模型的速度与密度的绝对百分比误差分别为2.76%和5.56%，速度辨识精度提升了41.5%,密度辨识精度提升了10.5%。图6为限速值75 km/h场景的仿真结果，一般可变限速模型的速度与密度的绝对百分比误差分别为3.23%和5.77%，本文提出交通流模型的速度与密度的绝对百分比误差分别为2.43%和5.43%，速度辨识精度提升了24.7%,密度辨识精度提升了5.89%。综上分析，本文提出的交通流模型能更加准确描绘雾天可变限速控制条件下高速公路的特性。