永磁同步电机常见故障建模与仿真研究

王小强，苏建徽

(合肥工业大学 电气与自动化工程学院，合肥 230009)

0 引 言

永磁同步电机(以下简称PMSM)运行可靠、控制灵活、效率高惯性低、输出转矩高，结构也简单，在电动汽车、航天等领域应用广泛。

近年来，出现了电机模拟器[1]的概念，专门用于模拟电机及其负载特性，它能够模拟与电机相同的端口电气特性，等效电机驱动器功率负载。其中，为测试电机驱动器在故障状态下的性能指标，需要获得能够模拟出PMSM常见故障的电机模型。

PMSM的数学模型在三种坐标系下各有优缺点。自然(a,b,c)坐标系下的模型适用性广泛；而同步旋转(d,q)坐标系下的模型完成了解耦，从而较自然坐标系下的模型容易不少[2]；静止(α，β)坐标系下，电机模型也实现了一定程度的解耦，且变换过程不需要坐标变换角，这在实际运用中也能节省一些DSP资源[1]。本文将分别在三种坐标系下进行了PMSM故障数学模型的推导及对比研究，以适应不同场合应用。

研究PMSM故障一般的模拟方法主要有两种[3]：一种是用有限元分析法(FEA)建立故障模型，另一种则是在PMSM数学模型基础上借助MATLAB/Simulink仿真平台研究。文献[4]对三相对称短路稳态特性进行了数学理论推导，通过二维有限元法和实验分析了永磁磁链、极对数、直流电感等电机本体参数对三相短路特性的交叉影响，但尚未从第二种方法来研究三相对称短路故障。PMSM定子匝间短路故障也可以采用有限元分析法建立模型，但通过采用有限元建模对PMSM故障进行仿真，虽然精度高，但效率太低，计算速度慢，难以施加控制策略和工况[4]。为克服上述缺陷，采用集中参数的数学模型在MATLAB/Simulink上仿真是一种有效的方法。在对自然(a,b,c)坐标系下定子匝间短路故障建模时：文献[5]对内置式PMSM进行了建模分析，由于表贴式PMSM电感较内置式PMSM简单，其模型可以进一步简化；文献[4]研究表贴式PMSM，寻求将模型建得十分精确，在计算电机电感时引入泄露因子δbf而使得模型变得较为复杂，需要进一步改进。在对同步旋转(d,q)坐标系下定子匝间短路故障建模时：文献[6]研究了五相PMSM，三相PMSM需进一步推导；文献[7]在对三相PMSM数学模型推导时未包含故障特征变量-短路电流if；文献[7]在计算if时需同时获得正常电机和故障电机的三相电压，使得电机模块翻倍而变得庞杂，需要进一步改进。文献[8]对自然(a,b,c)坐标系下三相PMSM开路故障进行了数学建模，但未进行有限元或者Simulink建模仿真以验证模型的正确性。在静止(α,β)坐标系下对PMSM的匝间短路故障和开路故障的数学模型研究较少，还需要进行进一步的理论推导。

为弥补上述研究的不足，本文重新推导了在自然坐标系、旋转坐标系和静止坐标系下三种故障状态下PMSM的数学模型，并在MATLAB/Simulink环境下进行了建模和对比仿真研究。

1 PMSM数学模型

三相PMSM由三相绕组及铁心构成，电枢绕组常以Y型连接，在转子结构上，PMSM用永磁体取代电励磁，省去了励磁线圈、滑环和电枢。

为便于分析，作以下假设：

(1) 忽略电机铁心的饱和影响；

(2) 永磁材料的电导率为零；

(3) 电机的电流为对称的三相正弦波电流；

(4) 不计电机的涡流和磁滞损耗。

在自然(a，b，c)坐标系下PMSM定子电压方程：

(1)

电磁转矩方程[9]：

(2)

式中:Uabc，Rabc，Iabc分别为三相绕组的相电压、相电阻和相电流；ψabc为三相绕组的磁链；Te为电磁转矩，p为极对数。在下面矩阵变量中，Ra=Rb=Rc=Rs为定子绕组电阻，ψf为永磁体磁链的值，L为电机自感，M为电机互感。

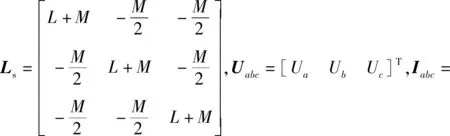
利用经典Park变换，可得在同步旋转(d,q)坐标系下的数学模型，定子电压方程：

(3)

电磁转矩方程：

(4)

式中:ud,uq为定子电压；R为定子绕组电阻；id,iq为定子电流；p表示微分算子；Ld,Lq为d,q轴等效电感；Te为电磁转矩；p为极对数；ψf为永磁体磁链。

利用Clarke变换，可得PMSM静止(α,β)坐标系下定子电压方程如下：

[(Ld-Lq)(ωeid-piq)+ωeψf]·

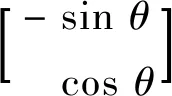
(5)

电磁转矩方程：

(6)

其中磁链方程：

式中:Uα，Uβ分别是PMSM在静止坐标系下定子电压；iα，iβ为定子电流；p表示微分算子；Rs为定子绕组电阻；Te为电磁转矩；p为极对数；ωe为电角速度；ψα，ψβ为永磁体磁链。

另外，PMSM运动方程：

(7)

转速、机械角速度、电角速度、角度公式：

(8)

ωe=pωm

(9)

(10)

式中：n为电机转速；ωm为电机的机械角速度；TL为负载转矩；ωe为电角速度；θ为转子位置角；J为转动惯量；B为阻尼系数。

2 PMSM三相短路故障下建模仿真

2.1 三相短路下数学模型

当PMSM莫明地发生三相对称短路时，产生的暂态冲击电流可能导致转轴与绕组端部的严重机械应力损伤，还有永磁体的不可逆去磁。但三相短路也可主动作为保护动作来应用，比如运行过程中其它故障原因导致电机失控，可以主动采取三相对称短路措施，隔离供电源保护电机，并且三相短路产生的制动转矩也将迫使电机减速至稳定。图1为PMSM三相短路示意图。

图1 PMSM三相短路示意图

三相对称短路稳态时，约束条件为定子三相电压突降为零，故在自然(a,b,c)坐标系下定子电压方程：

(11)

在同步旋转(d,q)坐标系下定子电压方程：

(12)

在静止(α,β)坐标系下定子电压方程：

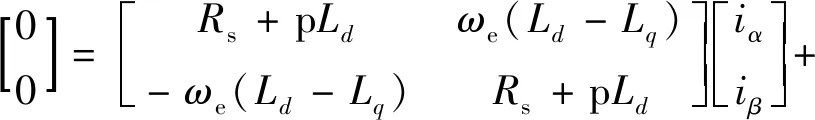
[(Ld-Lq)(ωeid-piq)+ωeψf]·

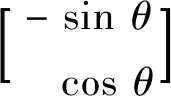
(13)

2.2 仿真验证

借助MATLAB/Simulink仿真平台搭建PMSM在故障状态下仿真模型，以验证以上参数模型的有效性和正确性，将之代入基于闭环速度和电流控制的简单三相PMSM矢量控制系统中，其中转速环是由PI调节器构成，电流环由电流滞环控制器构成，如图2所示。

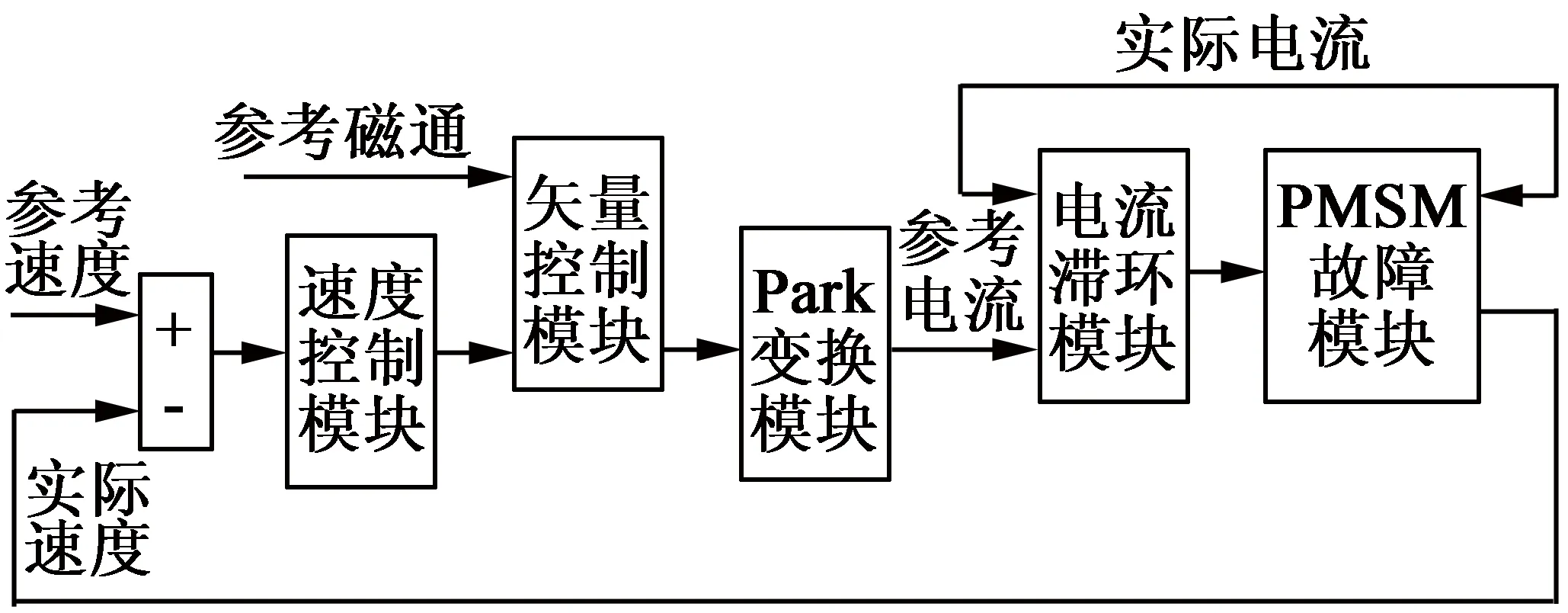
图2 PMSM矢量控制框图

用于仿真的电机主要参数如下：运行速度1 000 r/min，母线直流电压Udc=300 V，参考转速n=1 000 r/ min，极对数p=3，定子电阻Rs=1.5Ω，相自感L=1.725 mH，相互感M=0.028 mH，转动惯量J=0. 003 6 kg·m2，阻尼系数B=0.001 N·m·s。仿真条件设置：初始时刻负载转矩TL=5 N·m，在t=0.05 s时设置三相对称短路故障，获得的仿真波形如图3～图5所示。

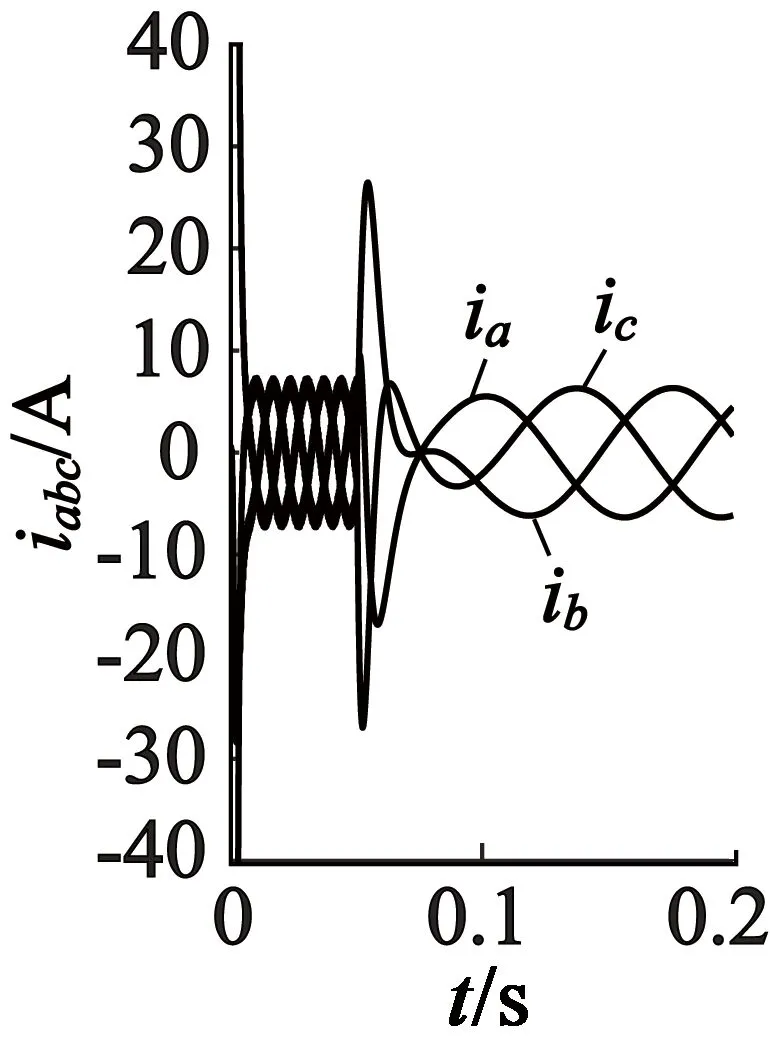
(a) a,b,c坐标系

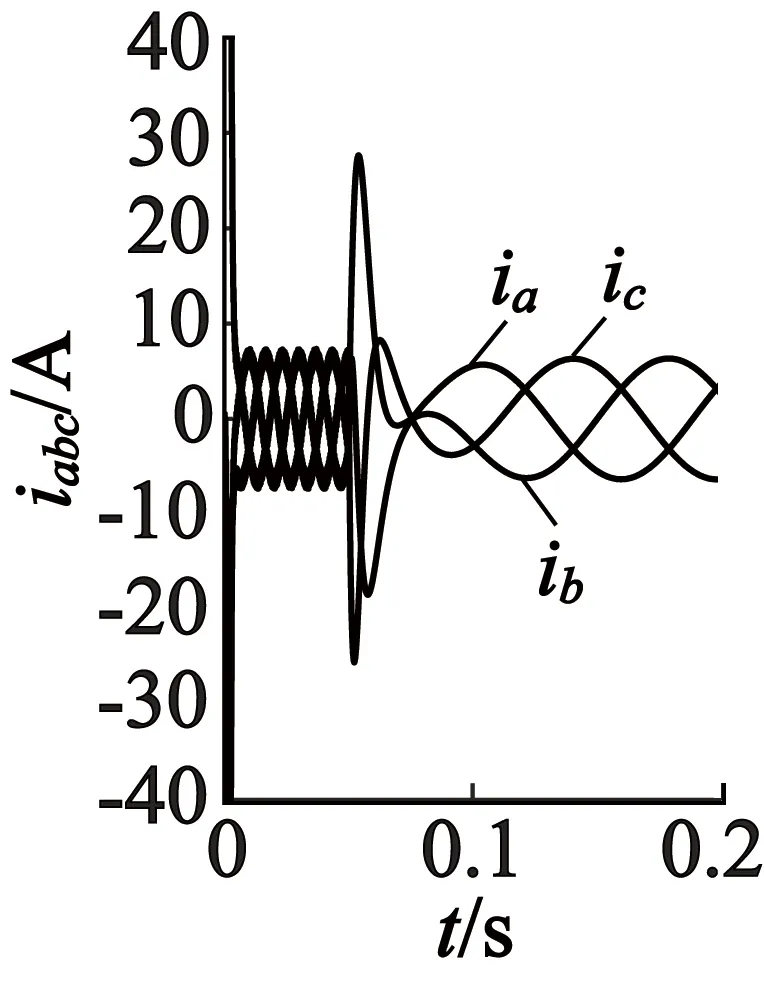
(b) d,q坐标系

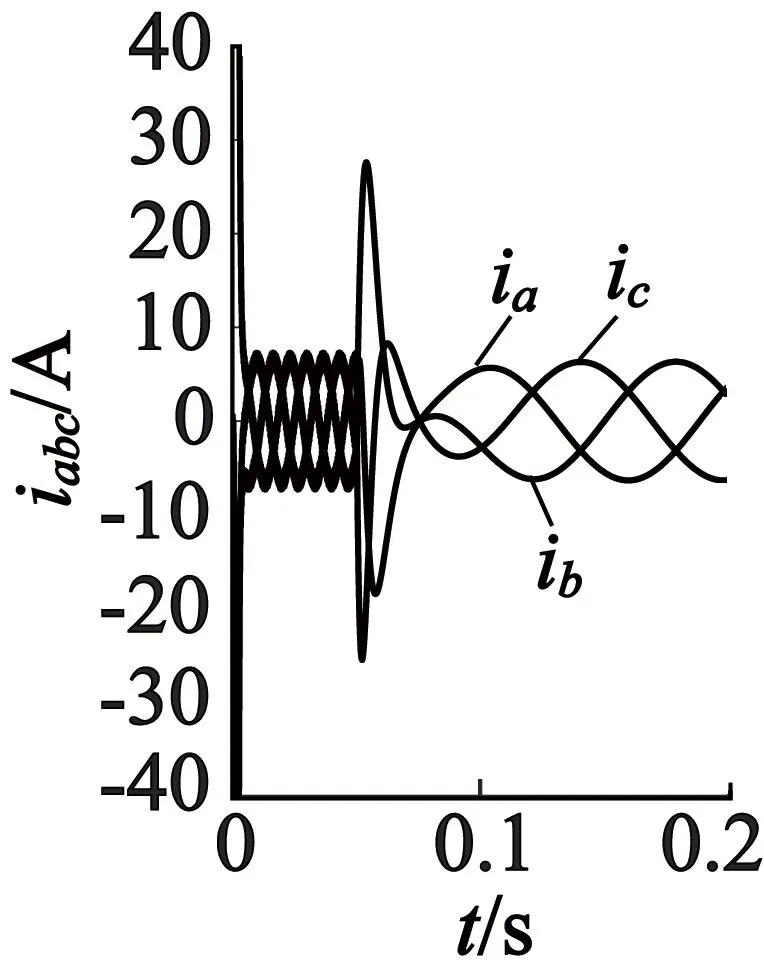
(c) α，β坐标系

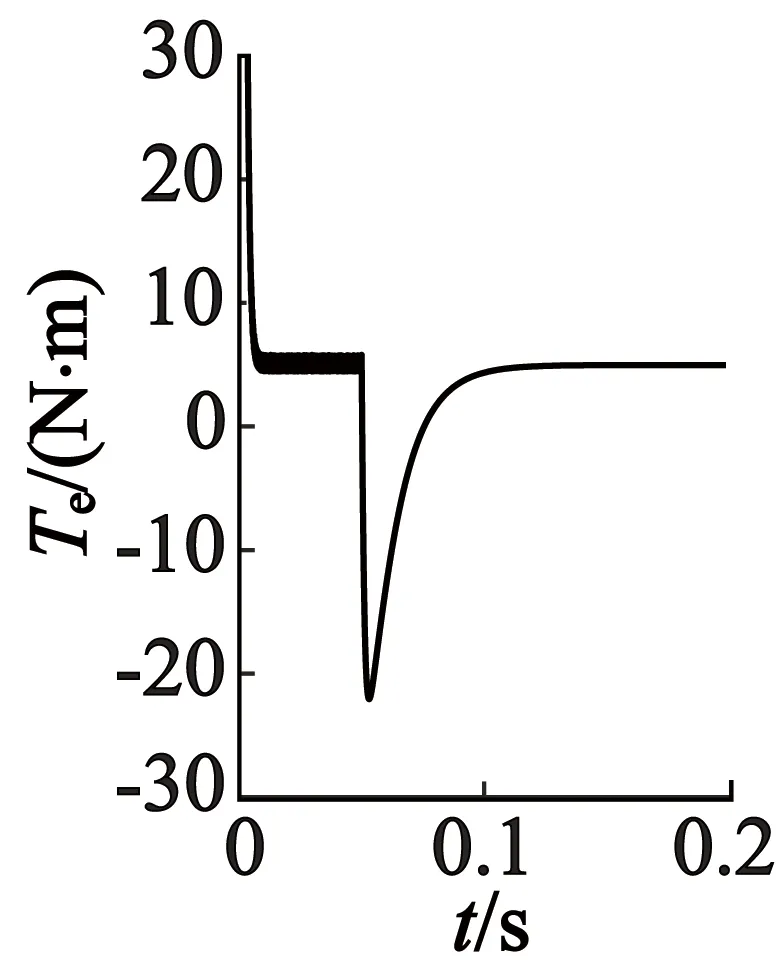
(a) a,b,c坐标系

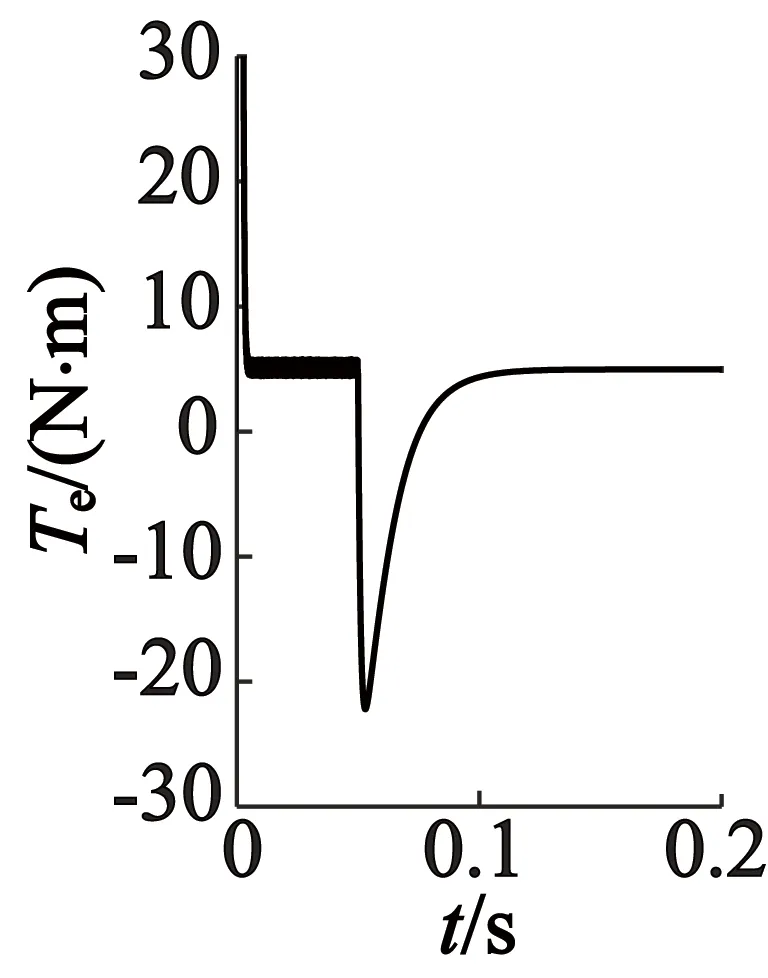
(b) d,q坐标系

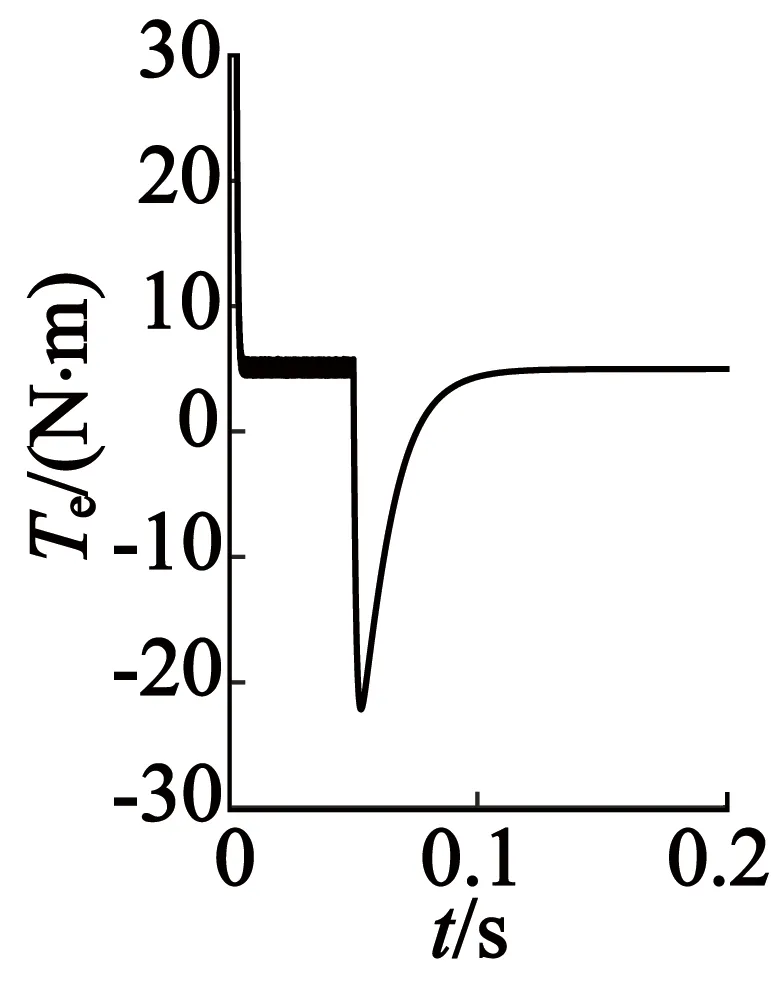
(c) α，β坐标系

(a) a,b,c坐标系

(b) d,q坐标系

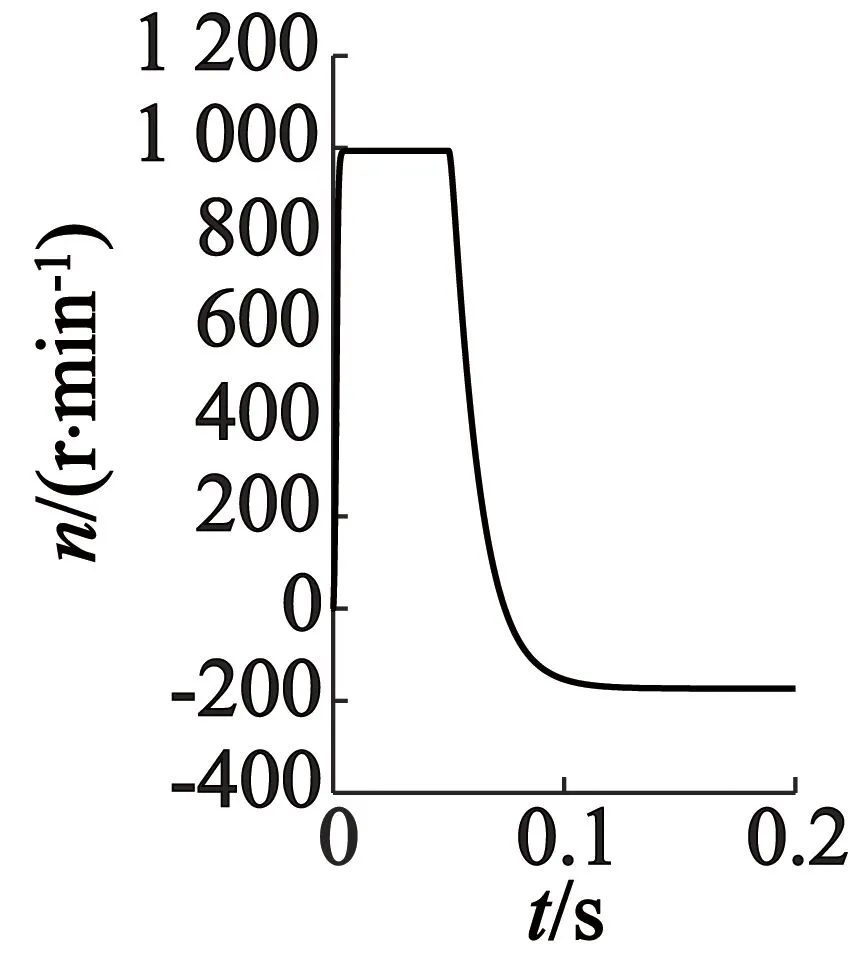
(c) α，β坐标系

由图3～图5可以看出，PMSM正常和故障时三种坐标下的电机三相电流、转矩及转速都十分接近。另外从波形可知，在0.05 s发生故障时，出现的瞬态三相电流及转矩都比稳态时大得多，此时出现的过电流是因为定子电压突降为零，导致定子磁链空间矢量变化率也降为零，因为定子磁链不能突变，在系统中产生定子磁链直流分量，进一步引起电机的过电流，之后电流回归稳态，转速也因三相短路产生的制动转矩在不断下降至稳定。

3 PMSM匝间短路故障下建模仿真

PMSM定子绕组匝间短路故障常常是因为绝缘损坏导致，此后也许还会引起更严重的损坏。假设PMSM发生A相匝间短路故障，n为短路匝数，N为故障相总匝数，rf为短路电阻，Rf为短路匝内电阻，R为相电阻，则故障示意图如图6所示。

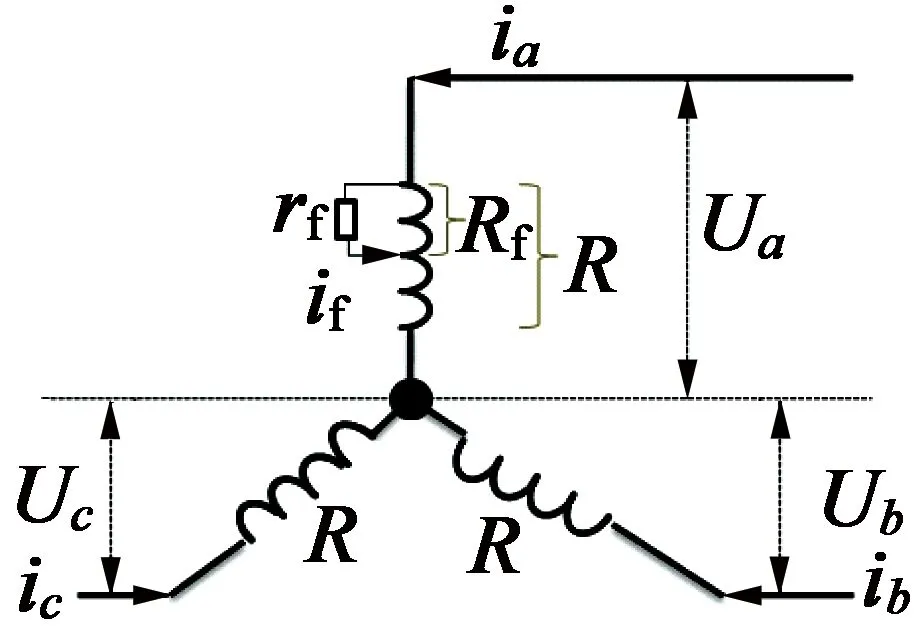
图6 PMSM A相匝间短路示意图

3.1 匝间短路故障在a,b,c坐标系下数学模型

与正常PMSM相比，发生匝间短路故障时电路中增加了故障环，假定用k表征故障的严重程度，通过分析，可得定子电压方程：

(14)

其中各变量的含义分别如下：

Rb=(1-k)Rs

Rf=k(Rs+rf)

ψabcf=LsfIabcf+ψfFabcf(θ)

3.2 匝间短路故障在d,q坐标系下数学模型

不考虑电机磁场饱和，当PMSM发生A相匝间短路故障时，PMSM在匝间短路故障情况下的电压方程式(1)可表示[10]：

(15)

当永磁同步电机A相发生故障时：

自然(a,b,c)坐标系变换到静止(α,β)坐标系的坐标变换为Clarke 变换；Park变换则是将静止(α,β)坐标系转化成同步旋转坐标系的变换。可通过Clarke/Park变换实现电机定子电压方程从自然(a,b,c)坐标系到旋转(d,q)坐标下的坐标变换：

Xdq=T(θ)Xabc

其中变换矩阵T(θ)：

定子电压方程(15)经过上述变换后：

(16)

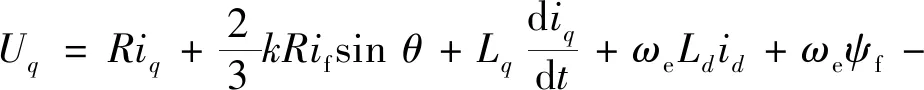
(17)

短路电流部分[11]计算公式：

而由d,q坐标系变换到a,b,c坐标系变换有：

Ua=Udcosθ-Uqsinθ

故可得：

(18)

3.3 匝间短路故障在α,β坐标系下数学模型

可通过Clarke变换实现的电机从自然(a,b,c)坐标系到静止(α,β)坐标下的坐标变换，与在同步旋转坐标下变换相似，当PMSM发生A相匝间短路故障时，可将式(15)由a,b,c坐标系变换为α,β坐标系：

Xαβ=X(θ)Xabc

其变换矩阵X(θ)：

(19)

对于表贴式PMSM，Ld=Lq，定子电压方程式(15)经过上述变换后：

(20)

(21)

短路电流部分等式：

而由反Clarke变换有：

Ua=Uα

故可得：

(22)

3.4 仿真验证

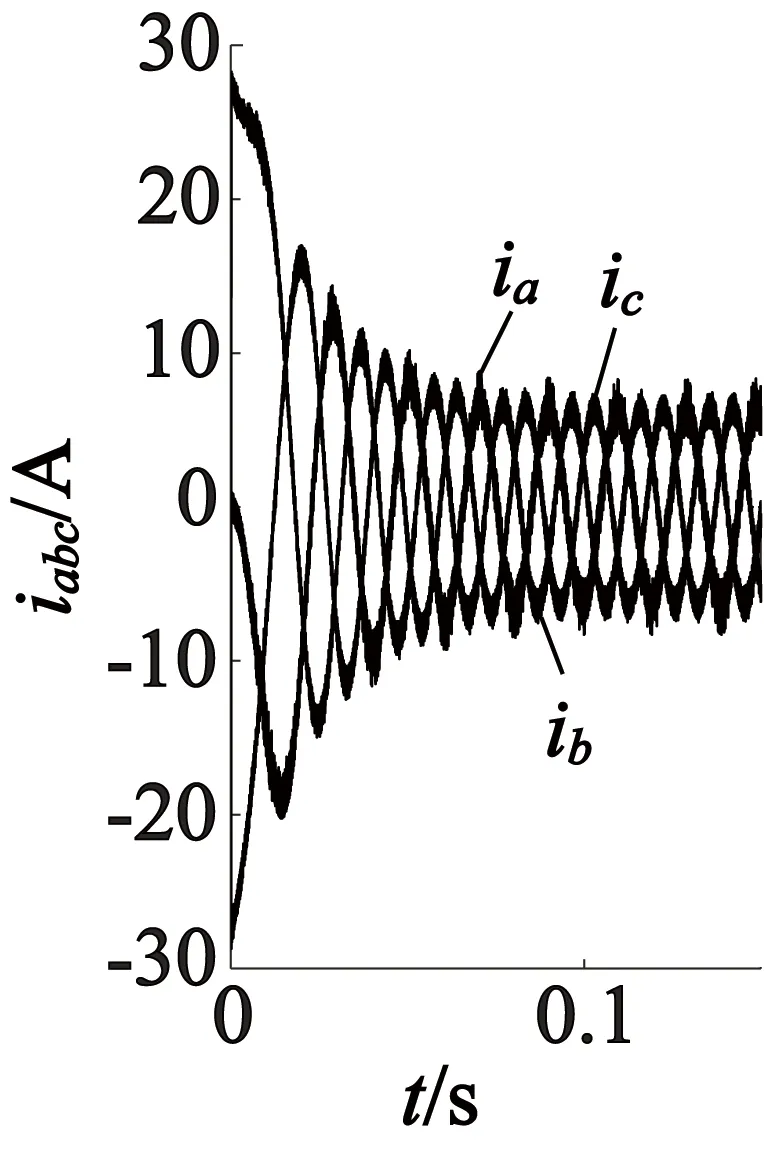
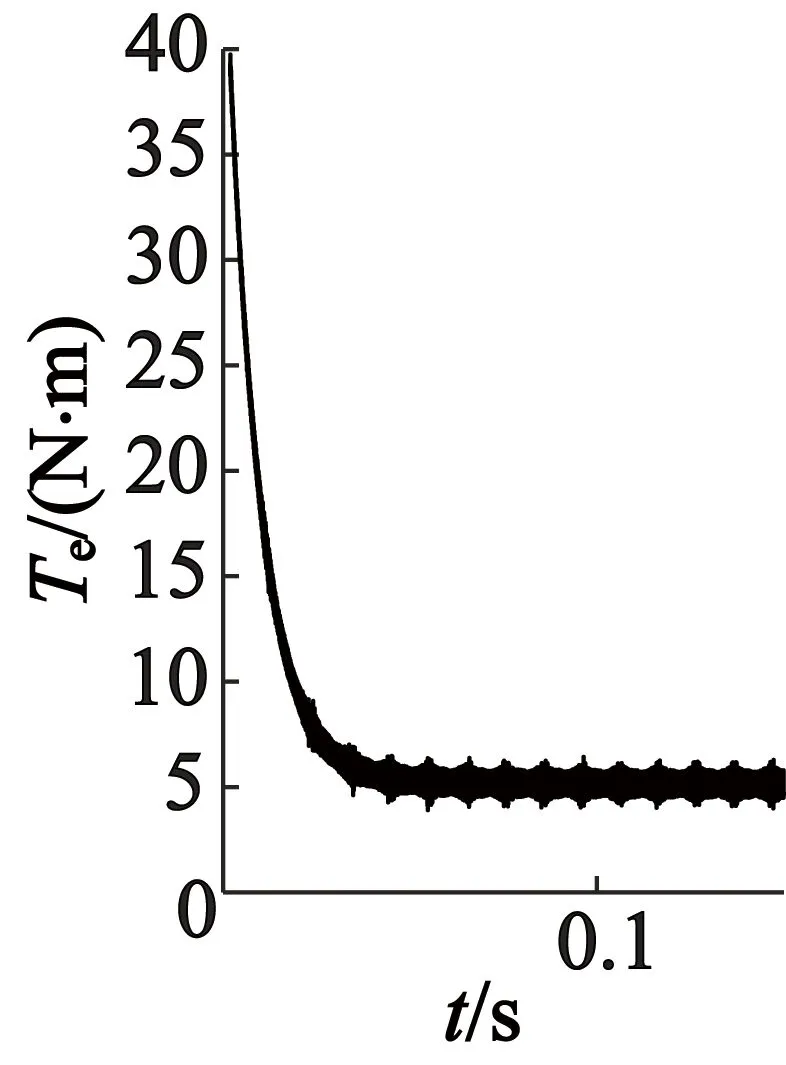
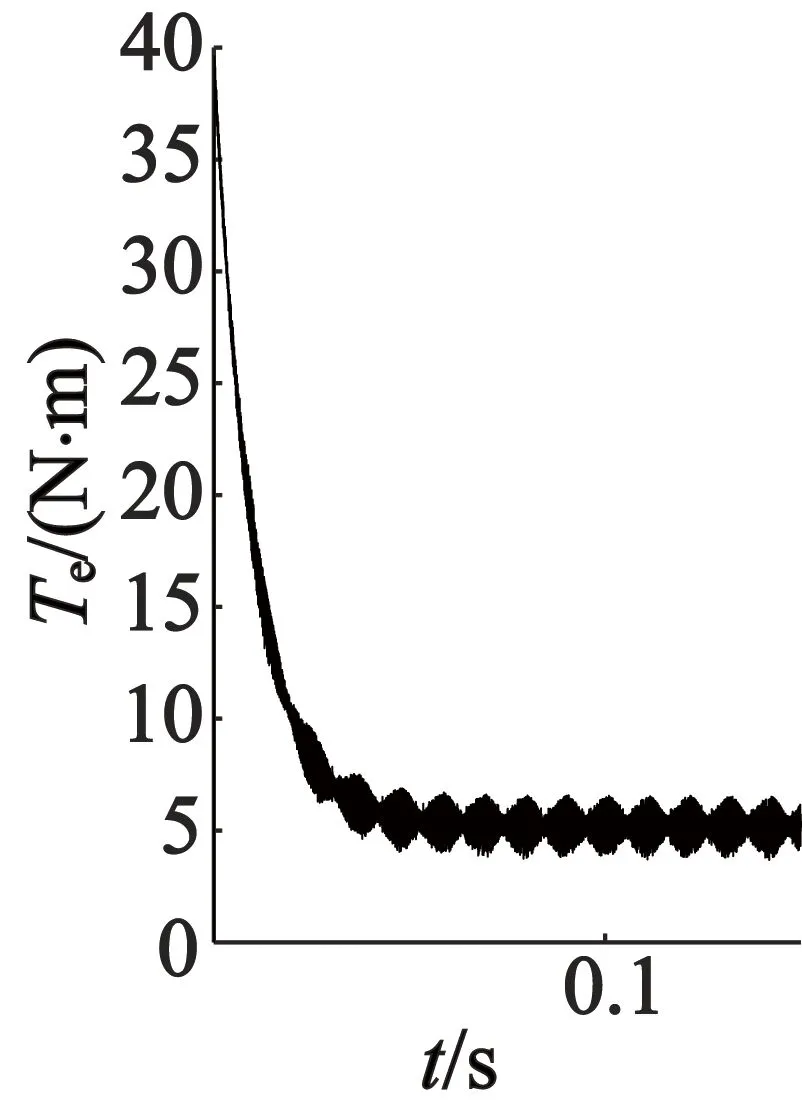
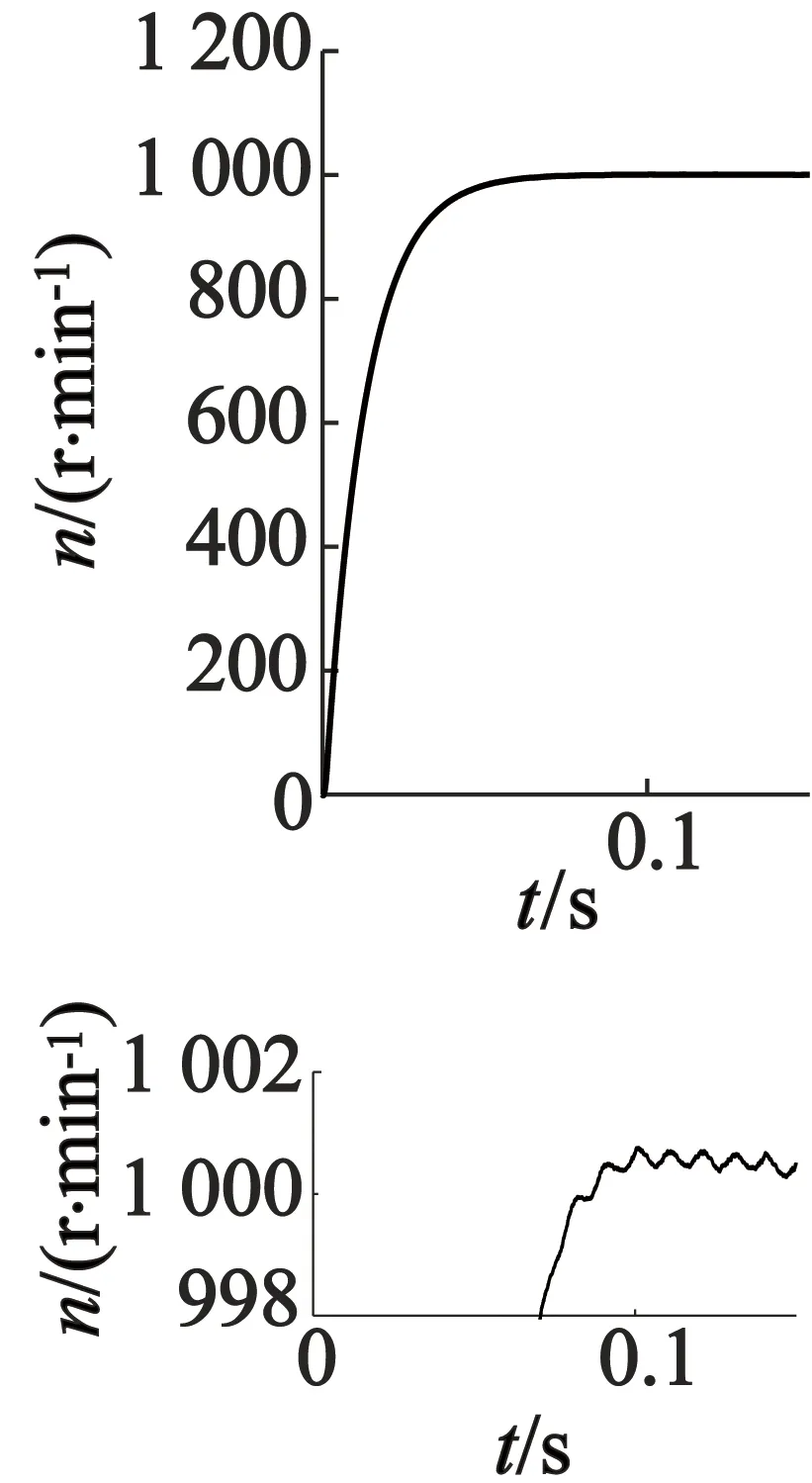
在上述同一PMSM的参数下，仿真条件设置：匝间短路故障系数k=0.3，初始时刻负载转矩TL=5 N·m，获得仿真波形，如图7～图9所示。

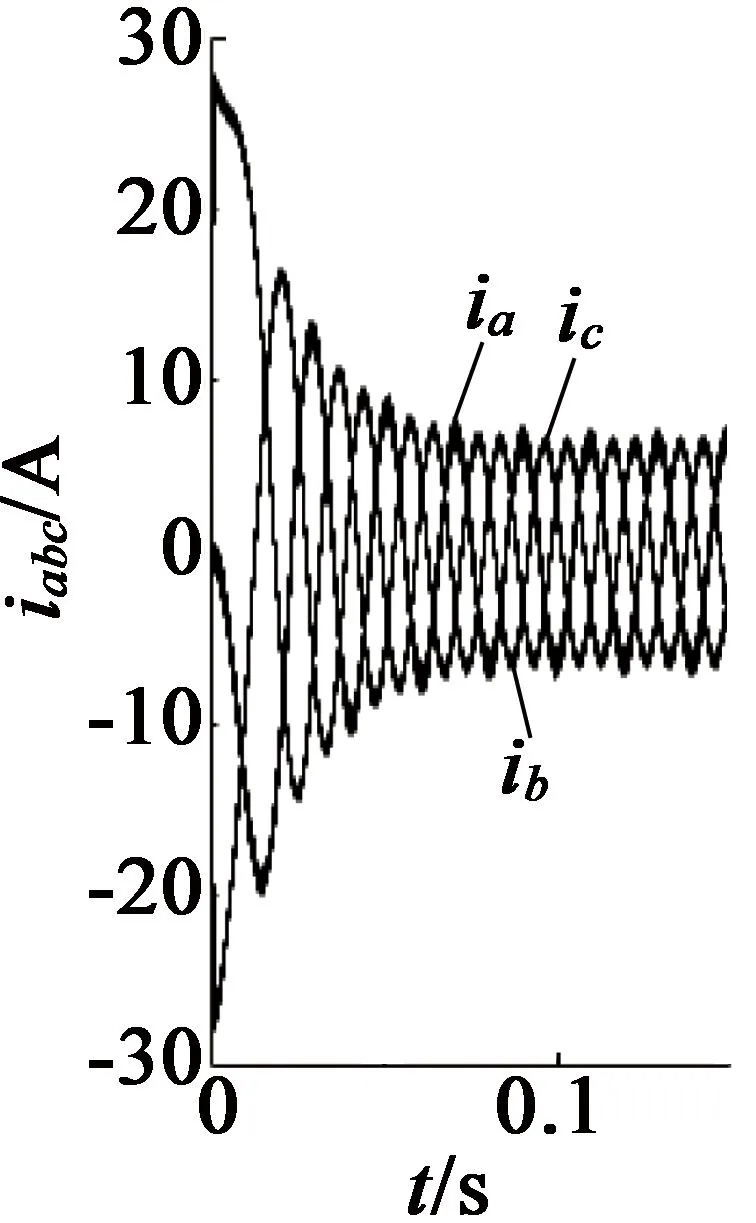
(a) a,b,c坐标系

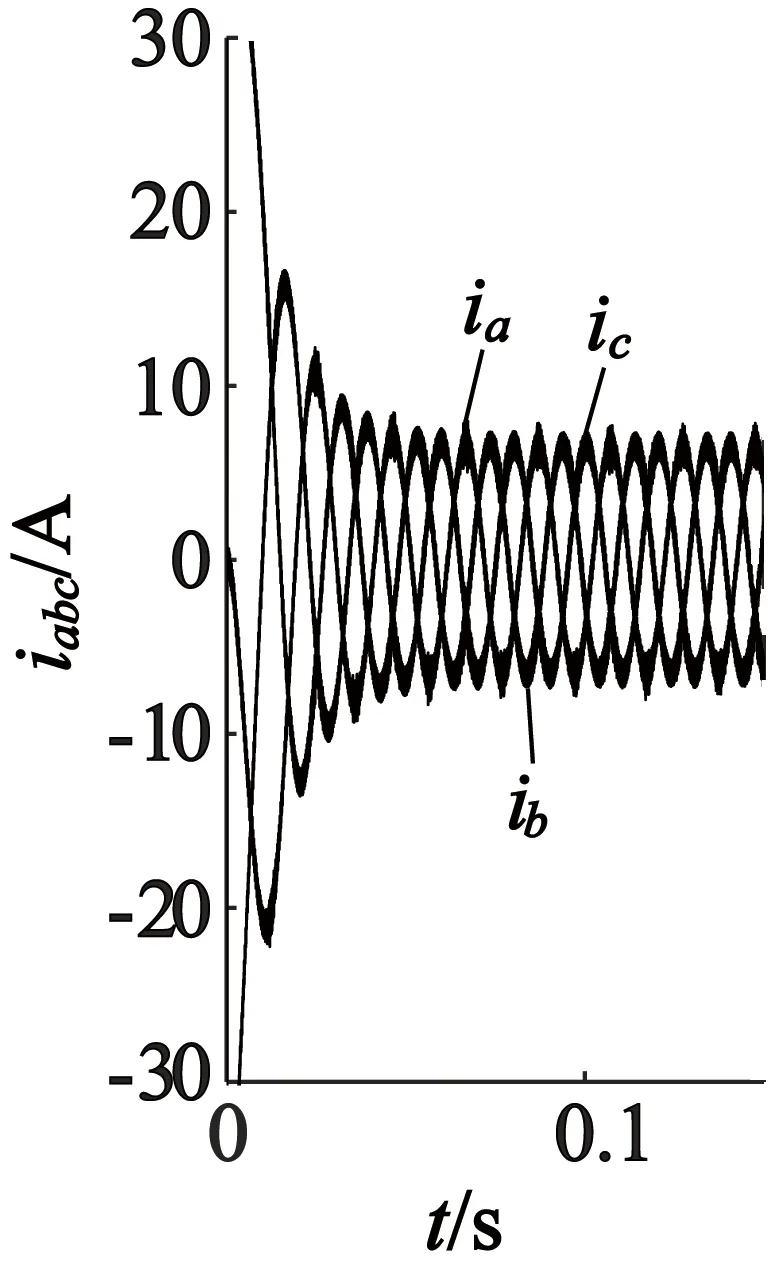
(b) d,q坐标系

(c) α，β坐标系

(a) a,b,c坐标系

(b) d,q坐标系

(c) α，β坐标系

(a) a,b,c坐标系

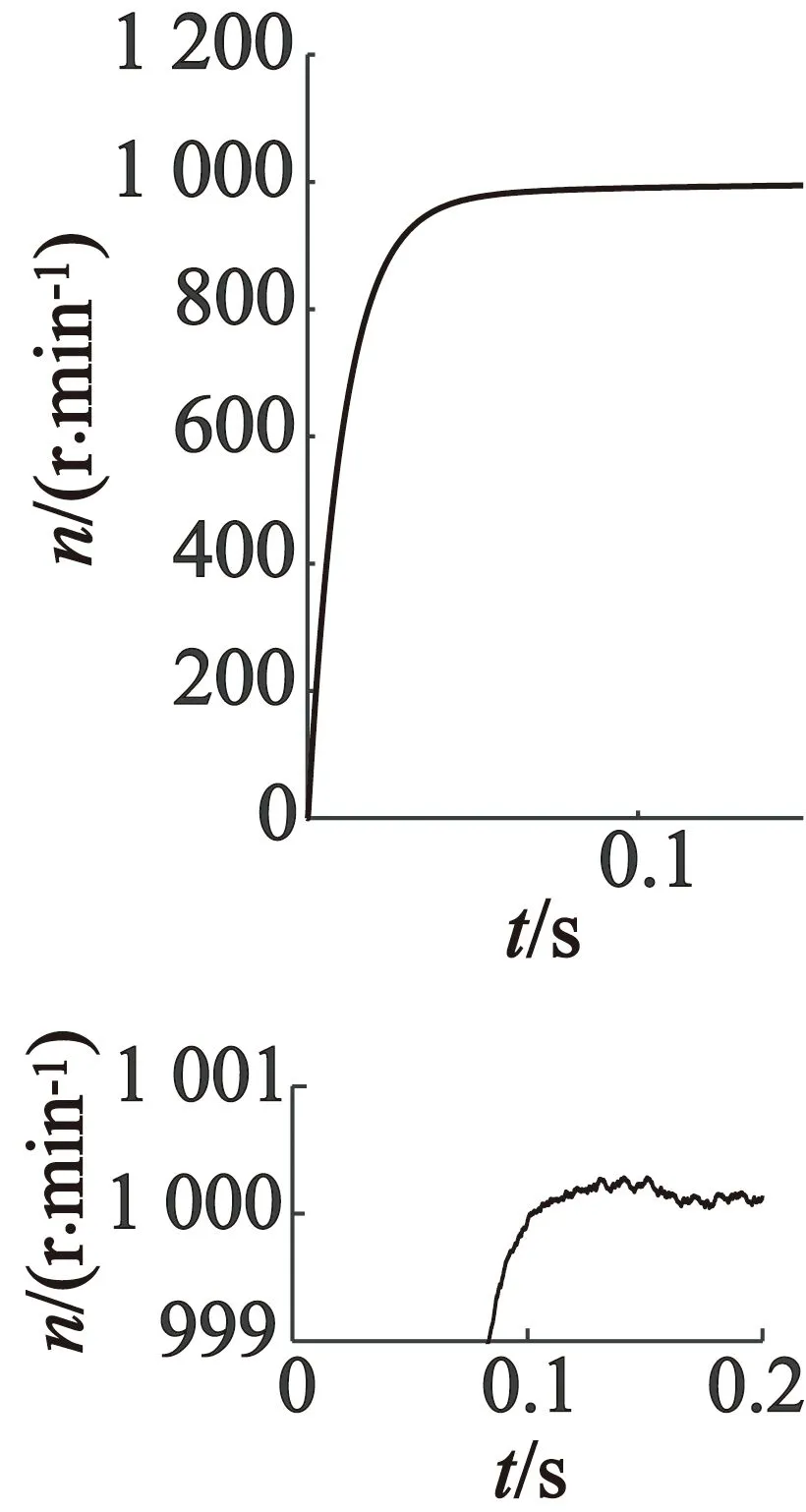
(b) d,q坐标系

(c) α，β坐标系

从以上仿真结果可以观察到：发生匝间短路故障时PMSM在三种坐标下的仿真波形很接近，不过通过PI调节器实现的电流闭环跟踪控制，难以消除电流跟踪误差， 因此三种坐标下的波形并不能完全一致[1]；在匝间短路故障时，故障A相电流幅值较其它两相更大[12]，这是由于绕组不对称，导致A相电流比其它两相电流有更为明显增大的高次谐波成分；电磁转矩和转速也产生了谐波成分，出现了小幅度波动。

4 PMSM开路故障下建模仿真

开路故障也是一种常见的电机故障。焊接不良，绕组短路，接地故障等都可以导致电机绕组开路。电机A相发生开路故障示意图如图10所示。

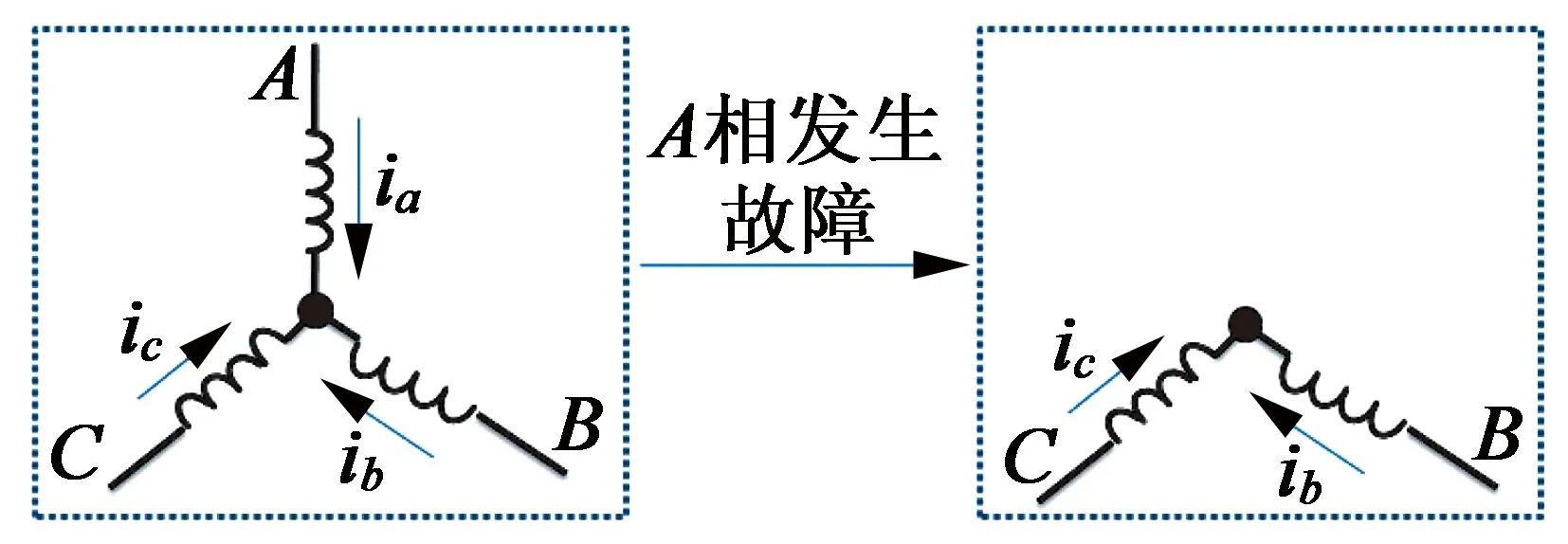
图10 PMSM A相开路故障示意图

4.1 开路故障在a,b,c坐标系下数学模型

假设定子绕组A相发生开路故障，则A相电压Ua=0[13]，三相电流不再对称[8,14]，A相电流由于电流传感器出现轻微偏差,导致ia=iΔ不为0，但十分接近0，通常认为ia=0，电流方程满足如下表达式：

(23)

故障时可代入定子电压方程：

(24)

式中:Ua，Ub与Uc分别为三相电压；ia，ib与ic为三相电流；Ra=Rb=Rc=Rs为定子绕组电阻；ψf为永磁体磁链值。

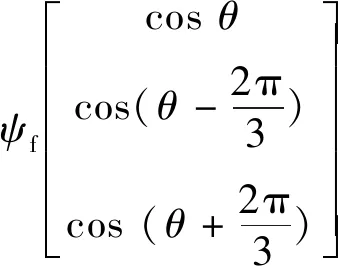
4.2 开路故障在d,q坐标系下数学模型

假定定子绕组A相发生开路故障，则通常认为ia=0。根据从同步旋转d,q坐标系到自然a,b,c坐标系的变换：

可得:

ia=0=idcosθ-iqsinθ

(25)

根据Clarke 变换：

得：

Uβ=Udsinθ+Uqcosθ

(26)

将d,q坐标系下的定子电压方程式(3)代入式(26)，则有：

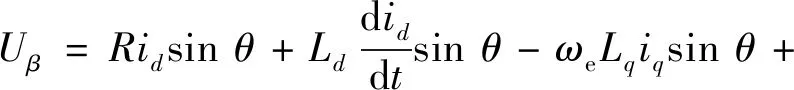
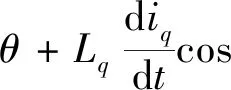
(27)

为了消除计算电流id，iq时出现在分母中的sinθ，cosθ引起的奇异点，引入两个辅助变量ρ和ξ，并令：

(28)

(29)

由式(25)可得：ρ=ξ，再将式(28)、式(29)代入式(27)，此时Uβ可用ρ变量表示，求解辅助变量ρ得：

(30)

求出ρ后，根据式(28)可得定子电流id，iq有：

(31)

此后即可顺利求出电机中角速度、转矩、转速等其它变量，建立PMSM开路故障的电机模型。

4.3 开路故障在α,β坐标系下数学模型

为不失一般性和利于计算求解，假定PMSM定子绕组C相发生开路故障，其实对于单相开路而言假定C相或A相发生开路故障等效，则C相电压Uc=0，且此时通常认为ic=0。根据反Clarke变换：

可得：

化简得：

(32)

根据Clarke变换：

PMSM静止坐标系下的定子电压方程式如下，对于表贴式PMSM而言,Ld=Lq，可进一步简化：

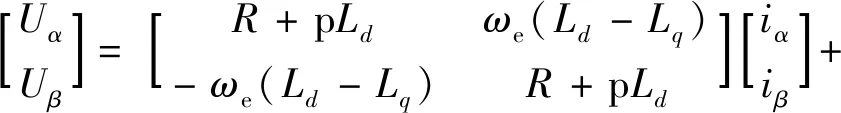
[(Ld-Lq)(ωeid-piq)+ωeψf]·

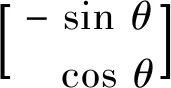
简化后代入可得：

(33)

在得到iβ后，利用式(32)可得iα，后可顺利求出电机中其它变量，获得α,β坐标系下电机开路故障时电机模型。

4.4 仿真验证

在上述同一PMSM的参数下，仿真条件设置：负载转矩TL=5 N·m，t=0.05 s时设置PMSM单相开路故障，获得仿真波形,如图11～图13所示。

(a) a,b,c坐标系

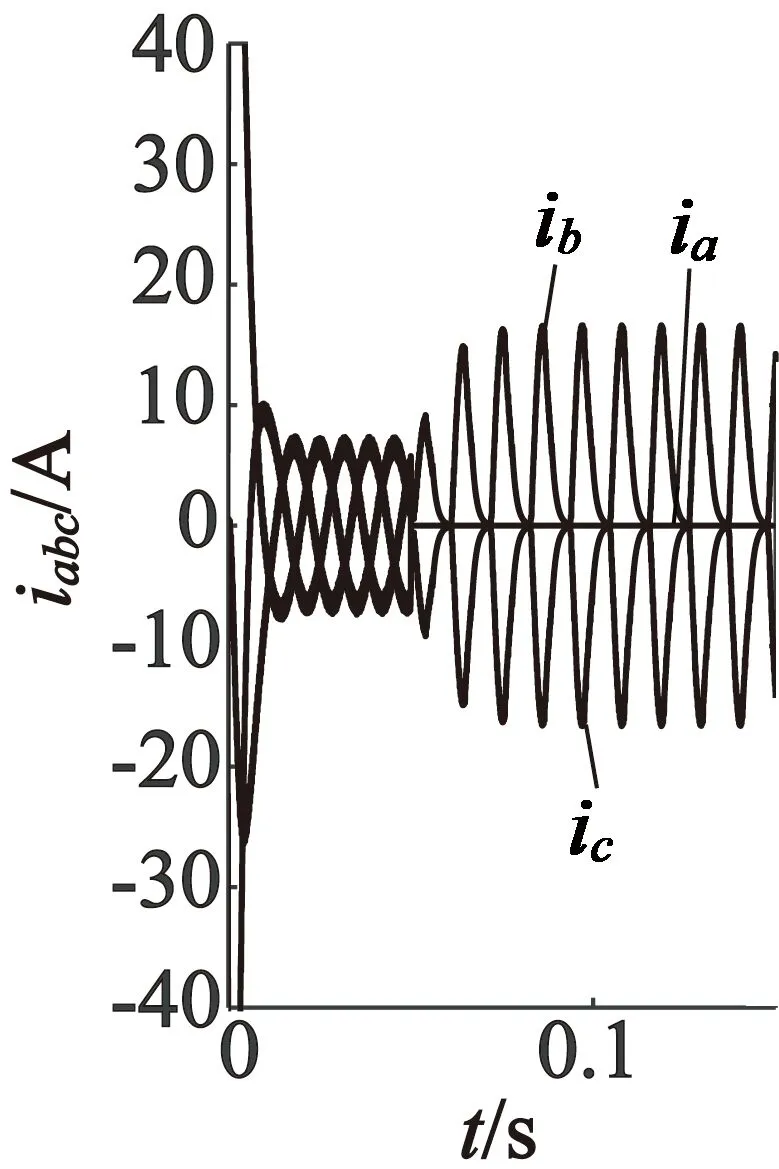
(b) d,q坐标系

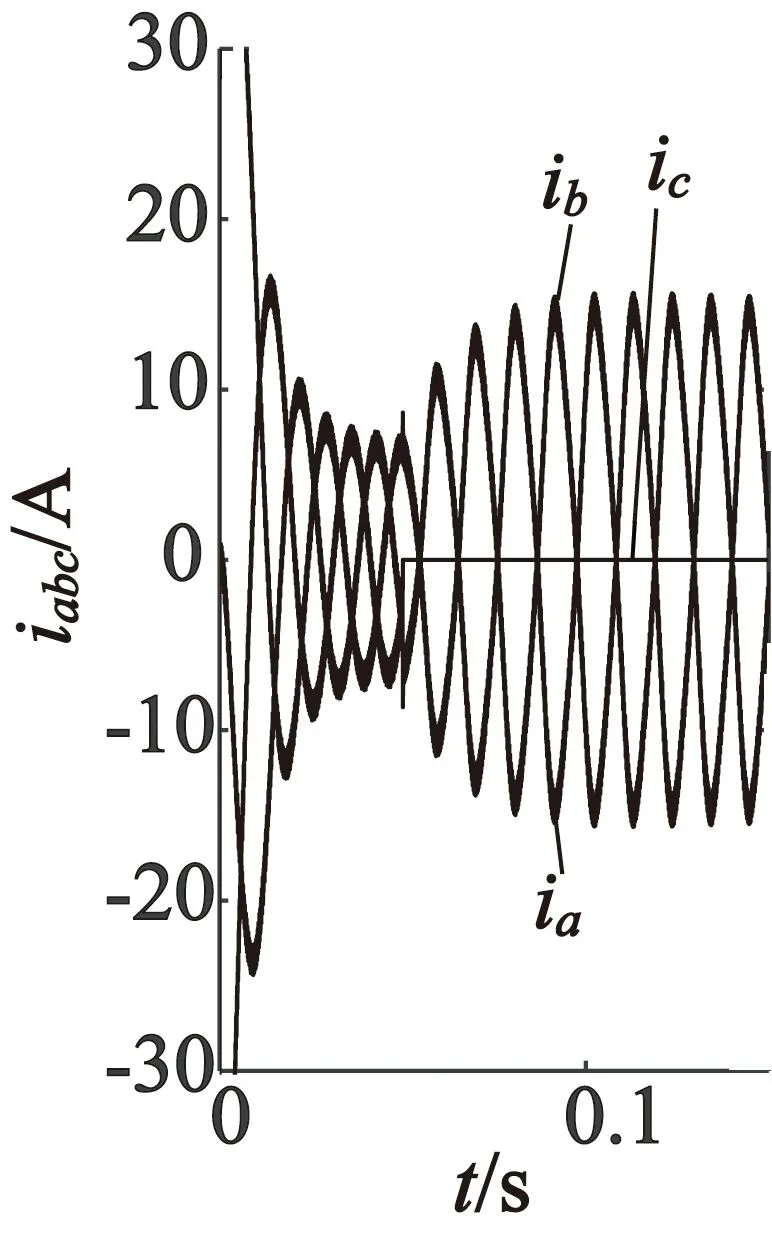
(c) α，β坐标系

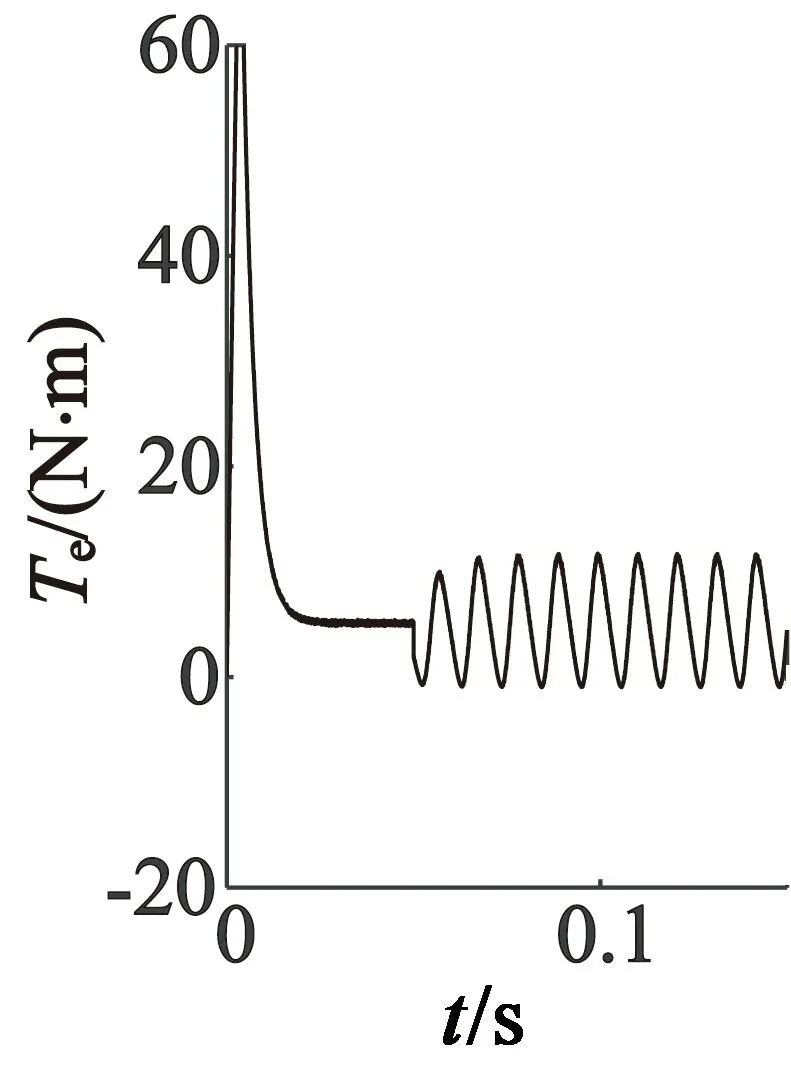
(a) a,b,c坐标系

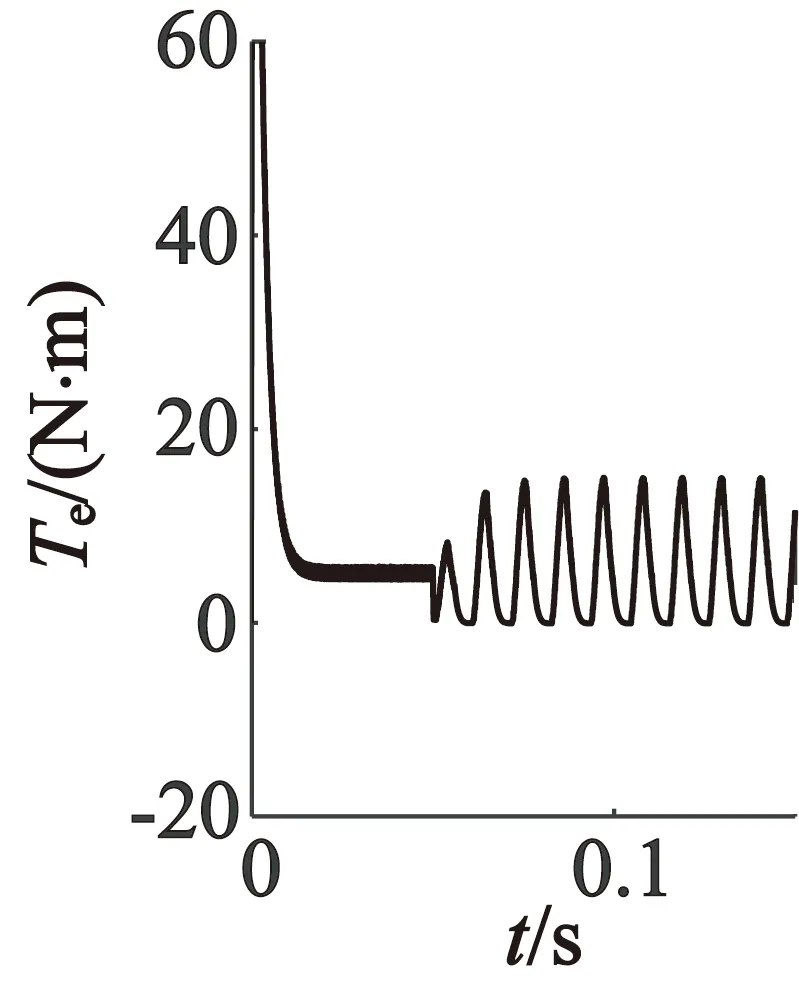
(b) d,q坐标系

(c) α，β坐标系

(a) a,b,c坐标系

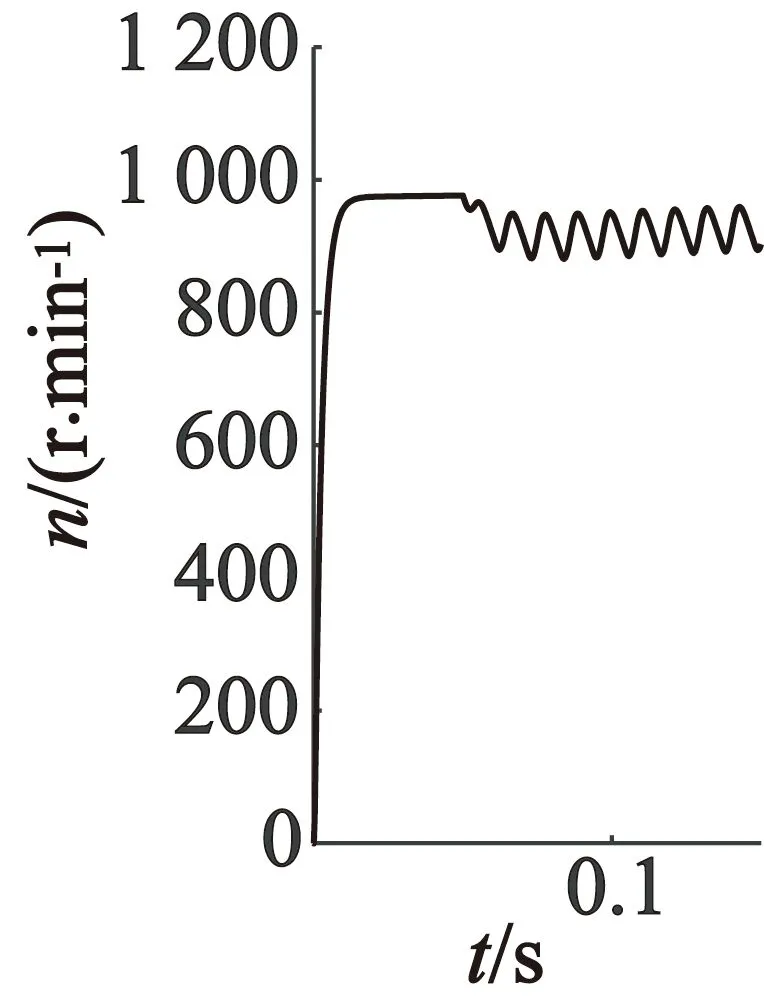
(b) d,q坐标系

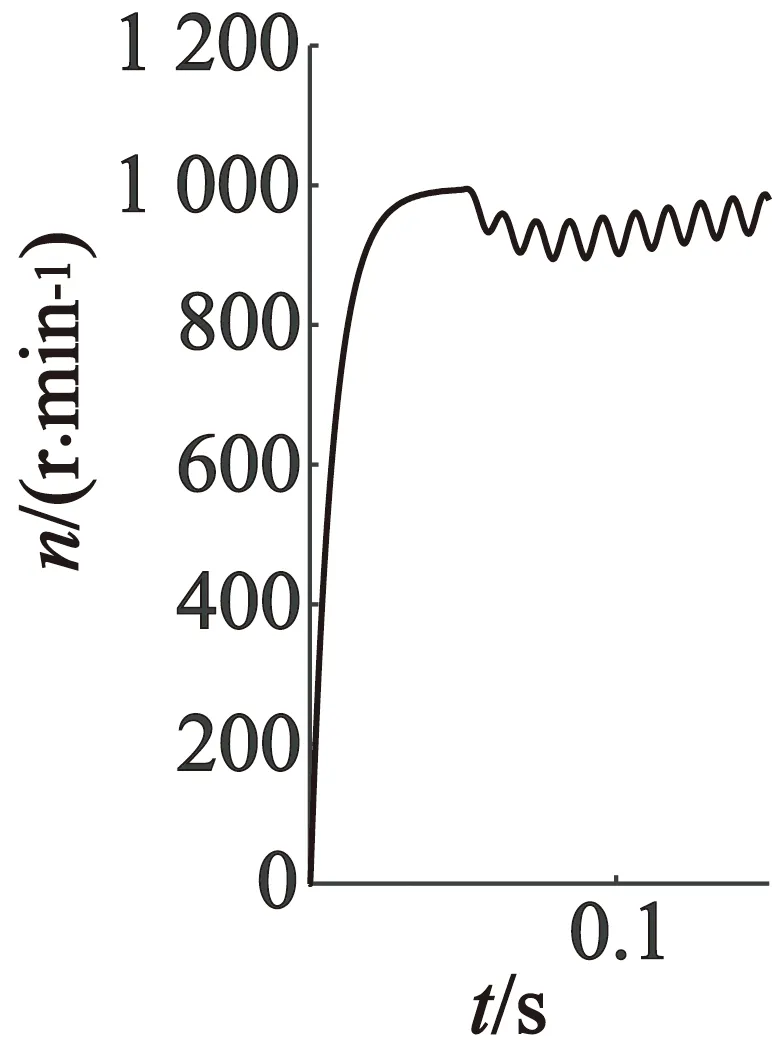
(c) α，β坐标系

从以上仿真结果可以看出，当PMSM发生单相绕组开路故障时，三种坐标系下的波形很接近。与正常运行时的0～0.05 s时间段相比，故障时三相电流的幅值比正常时幅值要大，并且此时PMSM的电磁转矩和转速都产生了较大脉动。这是由于当某相电流突变为零时，这相磁动势同样是零，而定子电流合成的磁势将会由圆形变成椭圆形，由此生成的椭圆形磁链将会生成接近电机转速频率的转矩脉动。

5 结 语

本文围绕PMSM三种常见故障，在三种坐标系下重新推导了数学参数模型，并采用MATLAB/Simulink建模仿真的方法来验证。仿真结果表明，三种坐标系下的PMSM故障下的波形很接近；同时获得了PMSM在三相对称短路故障，匝间短路故障和开路故障的故障特征信息，可作为故障诊断、故障容错和状态监测的研究基础。

本文在三种坐标系下都建立了PMSM的电机模型，能够满足在不同场合选择合适的数学模型，也为PMSM模拟器系统提供了可供选择的常见故障的电机模型，以此来测试电机驱动器在常见故障状态下的性能指标。