基于RSSI平均跳距路损的DV-Hop定位算法

周向，邹学玉 (长江大学电子信息学院，湖北 荆州 434023)

随着互联网技术的不断发展，室内无线定位技术在生活中的应用越来越广泛，例如大型商场、地下停车场等室内场景，这些地方人口相对集中，对人员、物品等位置信息有较高的需求。已知的定位技术，比如全球定位系统[1]和北斗卫星导航系统[2]，在室内定位精度上已经无法满足人们的需求，于是很多学者开展了关于室内无线定位技术的研究。经典的定位算法有基于测距的定位算法和基于非测距的定位算法[3]2大类。基于测距的定位方法有到达时间(time of arrival,TOA)[4]、到达时间差(time difference of arrival,TDOA)[5]、到达角度(angle of arrival,AOA)[5]和信号接收强度(received signal strength Indication,RSSI)[6～8]等。目前使用RSSI测距定位的算法较多，该技术主要使用radio frequency(RF)信号，根据接收信号强度值计算信号的传播损耗，按照相应传播损耗模型将传播损耗值转化为距离。这类方法具有较好的定位效果，但硬件成本高，能耗大。基于非测距的定位方法有质心法(centroid method)[7]、距离向量法(distance vector hop,DV-Hop)[9]、无定型算法(amorphous)[10]、近似三角形内点测试法(approximate point-in-triangulation test,APIT)[11]及凸规划法[12]等。这类方法能节省硬件成本，但定位精度不高。

针对上述2大类测距方法的优缺点，部分学者提出了多种改进方案：李凤超等[13]研究了一种无线传感器网络中改进的DV-Hop定位算法，该方法采用设置跳数阈值，并对跳数进行加权来求平均跳距，在一定程度上提高了定位精度；方旺盛等[14]结合DV-Hop与RSSI测距方法，提出设定一个基准值RSSIbasic，结合DV-Hop中每一跳的RSSI值来求出两者比值，以此作为跳数的方法；刘三阳等[15]利用信标节点的平均跳距误差，对未知节点与信标节点之间的距离进行了修正；Feng Xin等[16]给出了一种以RSSImax为参考对象的比值改进方案并由此提出了HCRDV-Hop算法；Omar等[17]提出了Hybrid DV-Hop算法，该算法主要是利用RSSI值把未知节点升级为信标节点，并循环优化位置信息。

上述方案在一定程度上提高了未知节点的定位精度，但依然存在一些问题，如跳距加权系数分母可能为0；以路损比作为跳数无法表征路损值与距离的非线性特性；DV-Hop全局平均跳距不能准确反映局部平均跳距。针对上述问题，笔者提出了基于RSSI平均跳距路损DV-Hop定位算法(average hop distance’s path loss DV-Hop，ADLDV-Hop)：首先改进跳距加权系数计算方法避免其分母为0；然后，对不同信标节点构造相应的估计平均跳距节点集，以提高局部范围的平均跳距准确性；最后，以平均跳距路损值为基准折合实际单跳路损值为非整跳数，以期减小节点间距估计误差。

1 无线信号传播损耗模型

基于RSSI的测距定位是获取无线网络节点位置信息的重要手段，常用的无线信号传播损耗模型[6]为：

(1)

式中:d为发射点与接收点之间的距离,m；PL(d)为阅读器收到距离为d时标签的RSSI值,dBm；d0为基准距离，通常为1m；PT为信号发射功率,dBm；pL(d0)为基准距离RSSI值,dBm；η为标量,表示路径损耗指数，一般取2～4；xσ为均值为0、方差为σ2的高斯噪声，4≤σ2≤10[19]。

某个节点i传播距离为d时的路损值记为：

(2)

在实际信号传播过程中，无线信号强度会随传输距离的增加而衰减，导致测量的RSSI值的相对误差增大，因此去掉信号较小的RSSI值，可以在一定范围上提高定位精度。以2.4GHz频段的无线信号传播RSSI值的ADAWifi测量数据为例[20]，对所采集数据拟合，得到RSSI值与距离的关系，结果如图1所示。

图1中包括了线性插值拟合折线和对数拟合曲线。由于RSSI值易受环境因素的影响，且该影响并不随着距离改变而变化，所以线性插值拟合折线会出现波动起伏；另外该折线反映了距离越远，RSSI值越小这一整体趋势。对原始数据使用最小二乘法进行对数拟合得到对数拟合曲线，该曲线验证了RSSI值与距离之间的对数关系。由于RSSI值是反映实际距离的信号强度数值，所以误差较小的RSSI值可以使距离的计算更精确。由于较小的信号强度不易被检测，会导致相对误差增大，因此，不使用RSSI较小的值计算距离可以提高定位精度，在笔者算法ADLDV-Hop中只取单跳的路损值作为测距依据。

2 DV-Hop算法基本原理

DV-Hop基本原理是通过计算信标节点两两之间的距离，然后信标节点将携带的信息传播给其它相邻节点，并在传播过程中记录不同信标节点之间的最小跳数[12～14]。该算法主要由距离矢量和节点之间的最小跳数来估计平均每跳距离，进而估计信标节点和待定位节点之间的距离。当某待定位节点得到至少3组到信标节点的距离信息时，使用三角形法或最小二乘法求出该节点的估计坐标。通过这种方法，可以利用少量的信标节点，求得较多的待定位节点坐标，并且定位范围较广。

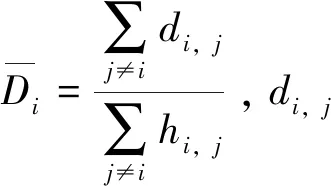
由于节点在平面上随机分布，不同节点之间跳数、跳距存在较大的差异性，导致实际坐标与利用DV-Hop算法估计的坐标之间有较大的误差。为解决算法中跳距方差过大使得定位误差较大问题，引入非整数跳数(即节点之间的跳数可以为非整数，如1.22数值)来降低定位误差。

3 ADLDV-Hop算法

3.1 跳数阈值

当两信标节点之间距离一定时，跳数值越高，表明传播路径越曲折，对平均跳距的影响越大。因此，去除不合理的跳数，能够有效的提高定位精度。对于信标节点i来说，最大跳数:

(3)

式中:R为节点通信半径,m；hi,max为最大跳数,保留2位小数。

3.2 平均跳距

3.2.1 平均跳距加权

在DV-Hop算法中，跳数与信标节点的通信半径具有强相关性，通信半径R越大，节点间的最小跳数越小。李凤超等提出的一种平均跳距加权方法采用式(4)对跳数进行加权[13]：

(4)

式中：wi,j为权重系数,1；m为参与以信标节点i为中心的平均跳距计算的其他信标节点总数,个。

3.2.2 平均跳距节点集构造法

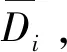
下面以图2为例说明平均跳距节点集构造法，并由此计算平均跳距。已知信标节点i,j1,j2,j3,j4,j5,j6，未知节点q1,q2,q3，节点通信半径R，其中j6为距离i最远的信标节点(距离2R)。得出最大跳数hi,max=2.00。

从图2中可以得到以下信息：j1,j3在通信半径内，i到j1,j3的最小跳数为1跳；i到j2的最小跳数为1跳，由于j2不在i及其有关节点的可达半径R内，则j2不参与i的平均跳距计算；j4在i的通信半径R外，但在j3的通信半径内(j3可与i节点通信)，因此j4最小跳数为2；j5,j6都在i的通信半径外，j5到i的最小跳数为2，j6到i的最小跳数为3，大于所设定阈值2.00，舍去j6。综合上述信息求平均跳距得：

(5)

3.3 节点间距离估计

节点间距离估计分覆盖与否2种情况。

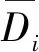
(6)

假设信标节点i(这里的i也可为未知节点)与覆盖的未知节点q之间的路损值pi,q(di,q)(简记为pi,q)，已知i，q之间的估计距离为d=Di,q，考虑随机噪声xσ均值为0，则由式(2)可得Di,q应满足：

(7)

则实际跳数为：

(8)

2)信标节点i不覆盖未知节点q但连通可达。若i到未知节点q之间存在多个不同传播路径，则Di,q取所有路径中的累加距离的最小值。具体方法如下：取节点i到未知节点q的每条可达路径上的相邻节点间的单跳路损值，若路径l(l=1,2,…,L)为i-j1-j2-…-jn-q(其中j1,j2,…,jn为未知节点),则路径l上每条链路的路损值为pi,j1,pj1,j2,…,pjn-1,jn,pjn,q，由式(6)计算每条链路距离，路径l的估值距离为：

(9)

3.4 未知节点坐标估计

设未知节点q与n(n≥3)个信标节点连通，，若n个信标节点的坐标分别为(x1,y1),(x2,y2),…,(xn,yn)，由式(8)或式(9)估算未知节点q到n个信标节点之间的距离分别为d1,q,d2,q,…,dn,q，用最小二乘法[18]求出未知节点q的坐标(xq,yq)。设待定位节点坐标为(xq,yq)，误差值为Vi，可列出误差方程如下：

(10)

令(X0，Y0)，(∂x，∂y)为待定位坐标的近似值与修正值。现设定X0=x1,Y0=y1，利用泰勒级数将式(8)线性化得到：

(11)

式(11)可以写作：

(12)

根据最小二乘法，即残差向量V和权矩阵A满足VΤAV为最小的条件下，求取未知数的最佳估值。 如当V=O时有最小平方差时，求解方程(18)得X=-(ATA)-1(ATL)，未知节点的坐标(xq,yq)为(x1+∂x,y1+∂y)。

3.5 ADLDV-Hop算法流程

算法流程图如图3所示。

4 算法仿真及数据分析

使用软件MATLAB2017b进行结果仿真。仿真模型为100m×100m区域大小。发射功率为40mW，信噪比为10dB，取RSSI噪声为xσ～N(0,4)[19]，假设信标节点和未知节点通信半径都为R。试验次数为50次，试验结果取其平均值。定义定位精度[14]评价指标为相对定位误差：

(13)

仿真分为2组进行：第1组与经典的DV-Hop算法和RSSI值测距定位算法进行对比，第2组与文献[15]中的BRDV-Hop算法和文献[17]的Hybrid DV-Hop算法进行对比。每组算法分别从节点通信半径、信标节点比例、节点总数3个方面进行对比分析，每次改变其中的单一变量。

4.1 ADLDV-Hop算法与其他算法的数据对比分析

选取空旷地区的路径损耗指数η=2,信噪比为10dB。

1)未知节点总数加上信标节点总数为100个，节点通信半径R=30m，信标节点比例在5%～45%范围内改变。图4反映了随着信标节点比例不断升高的过程中5种定位算法的相对定位误差逐渐减小这一整体趋势。当信标节点比例在5%～10%之间变化时5种对比算法的相对定位误差都高于30%，缺乏实际的定位意义；当信标节点比例在10%～40%之间变化时，5种算法定位精度提高明显，其中ADLDV-Hop算法相对于DV-Hop、RSSI测距定位、BRDV-Hop和HCRDV-Hop算法，其相对定位误差上分别减小了约10%、8%、7%、5%；在信标节点与节点总数比例在5%～45%范围内改变时ADLDV-Hop算法的定位精度优于其他4种算法。另外，从图4中可以看出，当信标节点比例高于40%时，信标节点比例增加所引起的定位精度提高趋于饱和，此时依靠增加信标节点比例来降低相对定位误差的性价比较低。

2)未知节点加上信标节点总数为100个，其中信标节点20个，未知节点80个，改变节点通信半径R。从图5中可以看出，当信标节点总数和节点比例一定时，增加节点通信半径，ADLDV-Hop算法相对于DV-Hop、RSSI测距定位、BRDV-Hop和HCRDV-Hop算法，其相对定位误差上分别最大减小提高了17.2%、13.3%、8.2%和7.6%；随着通信半径在10～40m的范围内增大，DV-Hop、RSSI测距定位、BRDV-Hop算法的相对定位误差下降趋势缓慢，而HCRDV-Hop和ADLDV-Hop算法的相对定位误差下降较为显著；通信半径从10m增至40m时，ADLDV-Hop算法的相对定位误差减小了6.6%，优于BRDV-Hop和HRCDV-Hop算法的相对定位误差减小值3.8%和3.2%。结果表明，在满足一定信噪比的情况下，ADLDV-Hop算法在节点通信半径增大时有利于提高定位精度。

3)保持信标节点与未知节点例为2∶8，且节点的通信半径为R=20m，节点总数在100～400个范围内变化。在通信半径R=20m的情况下，增加节点总数时保持信标节点比例不变，从图6中可以看出，ADLDV-Hop算法相对于DV-Hop、RSSI值测距定位、BRDV-Hop和HCRDV-Hop算法，其相对定位误差分别最大减小了11.2%、10.6%、6.2%和4.1%；随着节点总数的增加，5种算法相对定位误差均逐渐减小；当节点总数数量增加到3倍时，ADLDV-Hop算法的相对定位误差从28.0%下降到18.6%，BRDV-Hop算法的相对定位误差从32.0%下降到24.4%，HRCDV-Hop算法的相对定位误差从32.0%下降到22.5%。结果表明，依赖节点总数数量增加来提高定位精度需要付出较大代价，性价比不高。

4.2 不同信噪比和不同路径损耗指数对ADLDV-Hop算法相对定位误差的影响

1)保持节点总数为100个，信标节点与未知节点比例为2∶8，路径损耗指数η=2。对不同信噪比情况下的相对定位误差进行分析仿真试验，结果如图7所示。从图7中可以看出，在信噪比为5dB时，ADLDV-Hop算法相对定位误差为30.4%，随着信噪比的增大，相对定位误差逐渐减小；当信噪比为30dB时相对定位误差减小到5.1%；由此表明，信噪比增加，有利于ADLDV-Hop算法定位精度的提升。

2)保持节点总数为200，信标节点与未知节点比例为2∶8，信噪比为10dB。选取不同的路径损耗指数η，对3种算法(HCRDV-Hop算法、BRDV-Hop算法和ADLDV-Hop算法)进行仿真试验，结果如图8所示。从图8中可以看出，在路径损耗指数η取值范围内，随着路径损耗指数在2～4之间逐渐增加，3种算法相对定位误差都逐渐增加，但ADLDV-Hop算法相较于BRDV-Hop和HCRDV-Hop算法具有更高的定位精度。结果表明，路径损耗指数越高，ADLDV-Hop算法定位精度下降，但在相同条件下的定位精度优于BRDV-Hop和HCRDV-Hop算法。

5 结语

笔者提出的ADLDV-Hop算法，通过改进跳距加权系数，解决了可能出现跳距系数无限大的情况；针对不同的信标节点计算其平均跳距，克服节点分布不均匀带来对定位精度的影响；后以平均跳距及其参考路损折合实际路损来估算节点间距，增加了估计距离的准确性。相对于HVRDV-Hop和BRDV-Hop算法，在相同条件下，ADLDV-Hop算法进一步提高了定位精度；同时，增加节点通信半径和信噪比有利于提高定位精度。