高自然伽马致密砂岩储层参数解释模型
——以鄂尔多斯盆地大牛地气田D区为例
2020-05-25刘绪钢中国石化华北油气分公司采气一厂河南郑州450006
刘绪钢 (中国石化华北油气分公司采气一厂,河南 郑州 450006)
马先林 陕西省油气井及储层渗流与岩石力学重点实验室(西安石油大学) 西安石油大学石油工程学院,陕西 西安 710065)
复杂致密岩性体的勘探开发是当前油气领域的前沿问题,该类储层测井解释理论与处理技术也一直是石油地球物理学家们关注和探索的焦点[1~3]。鄂尔多斯盆地上古生界二叠系砂岩储层中均发现相对高自然伽马致密砂岩储层,具有可观的天然气储量和产能。该类砂岩储层常被误认为是泥质地层,因此其储层参数的测井计算方法应区别于常规砂岩储层[4,5]。下面,笔者以鄂尔多斯盆地大牛地气田D区为研究对象,充分利用已完钻井的测井、录井、测试、试气等资料开展综合研究,建立了一套适合大牛地气田上古生界高自然伽马致密砂岩储层泥质体积分数、物性参数的计算方法。
1 区域地质特征
大牛地气田位于鄂尔多斯盆地东北部(见图1),主要目的层为下二叠统太原组(P1t)、山西组(P1s)、下石盒子组(P1h)。晚古生代,碎屑物源主要来自盆地北部阴山山脉。P1t储层岩性为灰白-灰色中厚层状含砾石英砂岩、岩屑石英砂岩与黑色-深灰色泥岩、煤层,夹少量深灰色泥岩-微晶灰岩、生物碎屑灰岩;P1s储层岩性主要为中-粗粒岩屑砂岩,少量中-粗粒岩屑石英砂岩;P1h储层岩性为浅灰绿含砾粗-中砂岩,细砂岩夹棕褐及灰绿色泥岩,粉砂质泥岩和少量碳质泥岩,偶见煤线及砂质凝灰岩。研究区目的层储层致密砂岩测井曲线特征表现为自然伽马相对较高,高自然伽马致密砂岩储层与常规储层测井响应特征不同。高自然伽马致密砂岩具有相对高自然伽马、中-高声波时差、中-低电阻率的测井响应特征[6~8]。
2 储层参数测井解释模型
在测井资料标准化及岩心归位的基础上,根据岩心分析、岩电试验及地层水分析资料,分层位建立储层参数精细解释模型,包括泥质体积分数、孔隙度、渗透率及含水饱和度模型。
2.1 泥质体积分数
泥质体积分数反映地层岩性,与有效孔隙度、渗透率、含水饱和度、束缚水饱和度等储层参数密切相关[9~11]。研究区目的层存在钍含量较高的砂岩,直接用自然伽马曲线计算,其泥质体积分数较高,似为泥岩,而自然伽马能谱测井、录井、岩心分析及薄片资料均证实其为砂岩(见图2),且中子孔隙度、密度、声波时差三孔隙度曲线和电阻率曲线均显示无泥岩。自然伽马或无铀伽马曲线计算结果已不能真实反映地层泥质体积分数,因此,笔者提出自然伽马-中子孔隙度联合法计算泥质体积分数:
(1)
(2)
式中:φ(sh)为泥质体积分数,%;CGCUR为与地层年代有关的经验系数,新地层取3.7,老地层取2;Rlog为自然伽马或中子孔隙度读数;Gmax、Gmin为自然伽马或中子孔隙度相应曲线的最大值和最小值。
图2为B井泥质体积分数计算结果对比图,自然伽马-中子孔隙度联合法计算的泥质体积分数明显优于利用常规自然伽马计算的泥质体积分数。图3为自然伽马-中子孔隙度联合法计算的泥质体积分数与试验分析黏土体积分数结果对比图,自然伽马-中子孔隙度联合法计算的泥质体积分数极大地提高了计算精度。
2.2 孔隙度
研究区目的层P1t、P1s、P1h储层以石英砂岩、岩屑石英砂岩、岩屑砂岩为主,同时存在含灰质砂岩,已不是传统意义上的砂岩,而是多种岩性混积的复杂岩性体。计算储层孔隙度的关键在于如何确定复杂混积砂岩的骨架参数值。
首先,利用岩心资料刻度测井资料,由岩心分析密度确定各层位混积砂岩骨架密度和声波时差;因各层位砂岩岩性不同,再结合岩性即可确定相应砂岩骨架参数值。各层位不同岩性砂岩骨架参数如表1所示。
确定各层位不同岩性砂岩骨架参数值后,即可应用体积模型计算储层砂岩孔隙度φ:

(3)
(4)
(5)
式中:φs为声波时差计算出的孔隙度,1;φD为密度孔隙度,1;Δt为声波时差,μs/m;Δtma、Δtf分别为岩石骨架、地层流体声波时差,μs/m;CP为声波压实校正系数,可利用岩心分析孔隙度与声波计算孔隙度求得,1;ρma、ρf分别为岩石骨架、地层流体密度,g/cm3;ρ为目的层密度,g/cm3;ρsh为泥岩密度,g/cm3。
图4为岩心物性分析与测井计算的孔隙度、渗透率结果对比图,分析表明,体积模型法计算的孔隙度与岩心分析孔隙度较为符合。原孔隙度计算模型采用的是纯砂岩骨架参数值,而新模型是根据不同岩性采用不同骨架参数值。图5为测井计算孔隙度与岩心分析孔隙度模计算结果对比图,分析可知,新模型计算精度大大高于原模型计算精度。
2.3 渗透率
根据岩心分析数据,分层系建立孔隙度-渗透率的相关关系,得到P1t、P1s、P1h储层渗透率模型(见表2)。测井计算渗透率参数与岩心分析渗透率结果较为符合。该次渗透率参数解释精度较已往大幅度提高。
2.4 含水饱和度
分析大牛地气田D区及邻区上古生界储层物性及孔隙结构条件,储层属含少量泥质、中等孔隙、以粒间孔和粒内溶孔为主的孔隙型储层。因此,选用阿尔奇饱和度模型计算含水饱和度:
(6)
式中:Sw为含水饱和度,1;ρt为地层电阻率,Ω·m;ρw为地层水电阻率,Ω·m;φ为孔隙度,1;a、b、m、n为与岩性及孔喉结构有关的岩电参数。
根据试气及生产实际状况,确定含气饱和度(Sg)界限。气层:Sg≥50%;差气层:50%>Sg≥35%;含气层:Sg<35%。
2.4.1 岩电参数
由岩电试验分析结果,得到各层位岩电参数如表3所示。
2.4.2 地层水电阻率
地层水电阻率计算公式如下[12~14]:
ρwN≈0.0123+
式中:CwN 为24℃或75℃时地层水总矿化度, mg/L(NaCl);ρwN为24℃或75℃时地层水电阻率,Ω·m;t为地层温度,℃ 。

表2 各层位渗透率相关关系
注:P1t1、P1t2为太原组一段、二段;K为渗透率,mD。
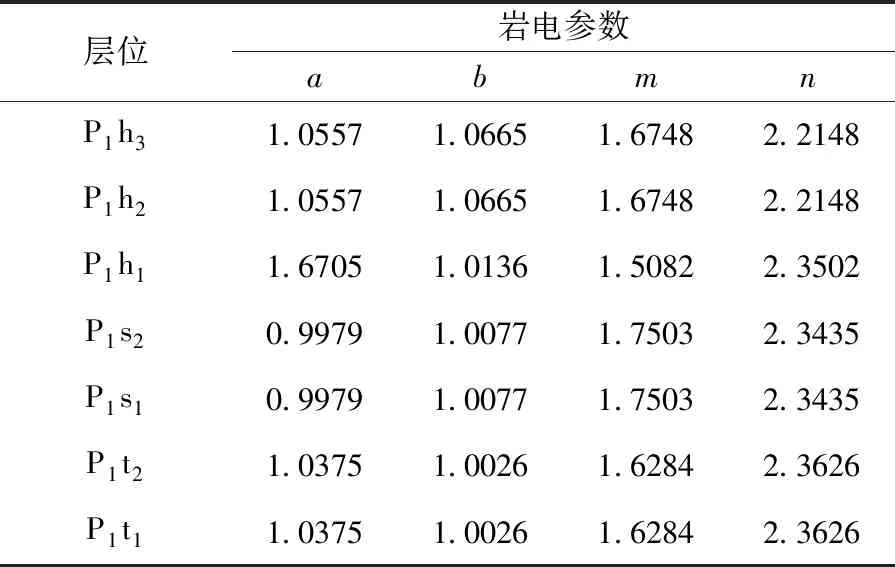
表3 岩电参数a、m、b、n取值表
选取测试返排率大于100%的储层反推地层水电阻率,根据地层水分析数据确定各层位的地层水电阻率,P1h3、P1h2、P1h1、P1s2、P1s1、P1t的ρw分别为0.144、0.132、0.131、0.132、0.099、0.071Ω·m。该地层水计算方法解决了前期因地层水变化大引起的地层水电阻率多变问题。将地层水电阻率代入式(6),即可计算含水饱和度。
B井一次解释与笔者研究解释结果的对比情况如图6所示。对比2次含水饱和度解释结果,该次含水饱和度研究解释结果与产能测试匹配更好,解释结果得到了测试结果的验证。
3 解释结果验证
由前述测井资料处理及参数计算,结合测试资料总结研究区各层位的测井解释标准如表4所示。
根据所建立的解释标准和储层参数解释模型,对D区225口井储层参数重新进行计算,并确定解释结论。经岩性分析验证,该次研究所建立的分层位、分岩性的优化解释模型较以往的解释模型有较大
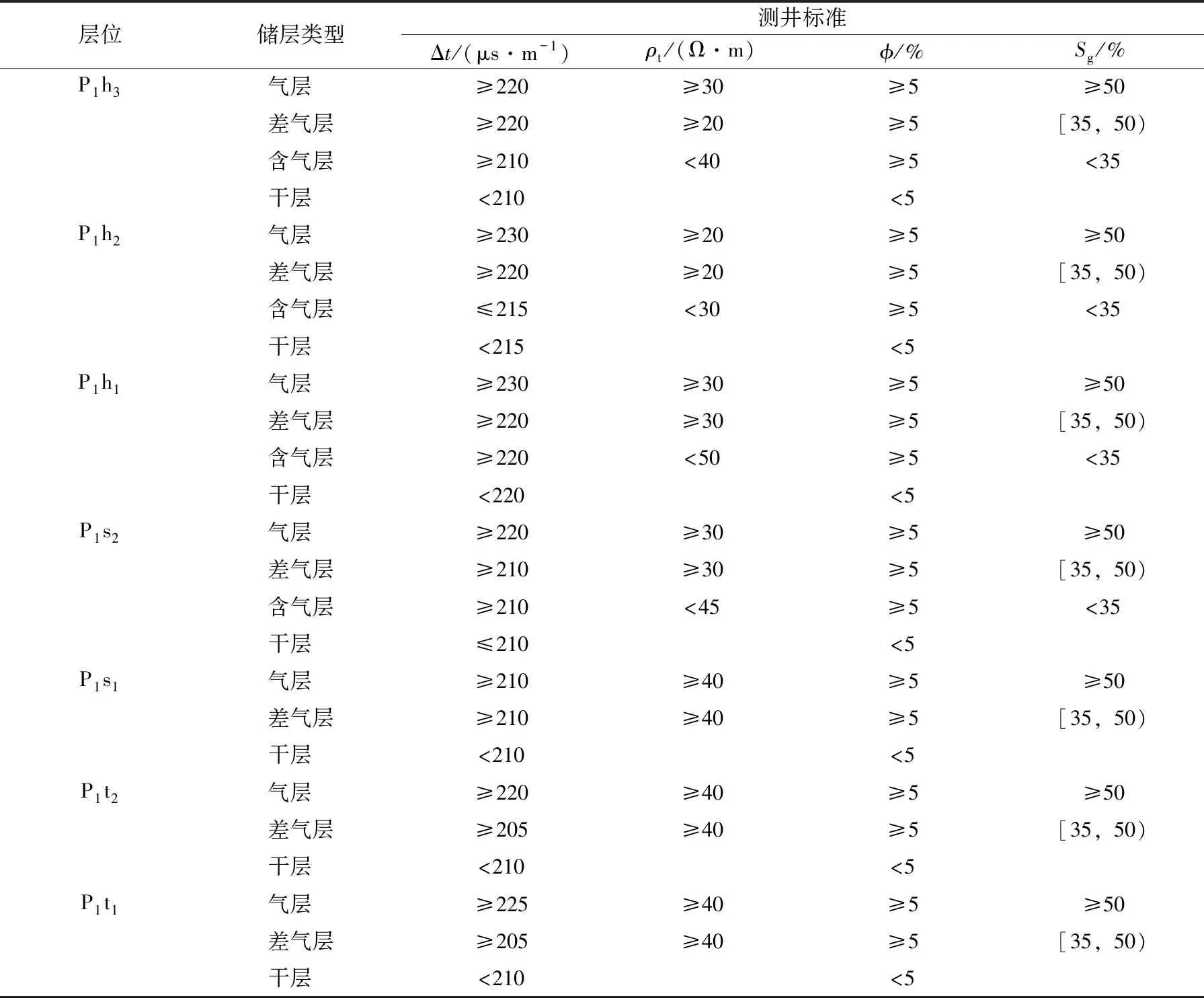
表4 各层位测井解释标准
改进,其解释成果得到试气资料的验证。典型井B井二次解释结果如图6所示。分析图6,25(4)、25(6)层原解释结果为非储层,新模型处理解释结果为储层,计算的孔隙度、渗透率参数与岩心分析结果较为符合;25(1)、25(5)、25(7)层原解释结果差气层,新模型处理解释结果为气层,与测试结果(日产气量0.8782×104m3,日产水量0.97m3)符合。该段储层测井二次解释成果见表5。
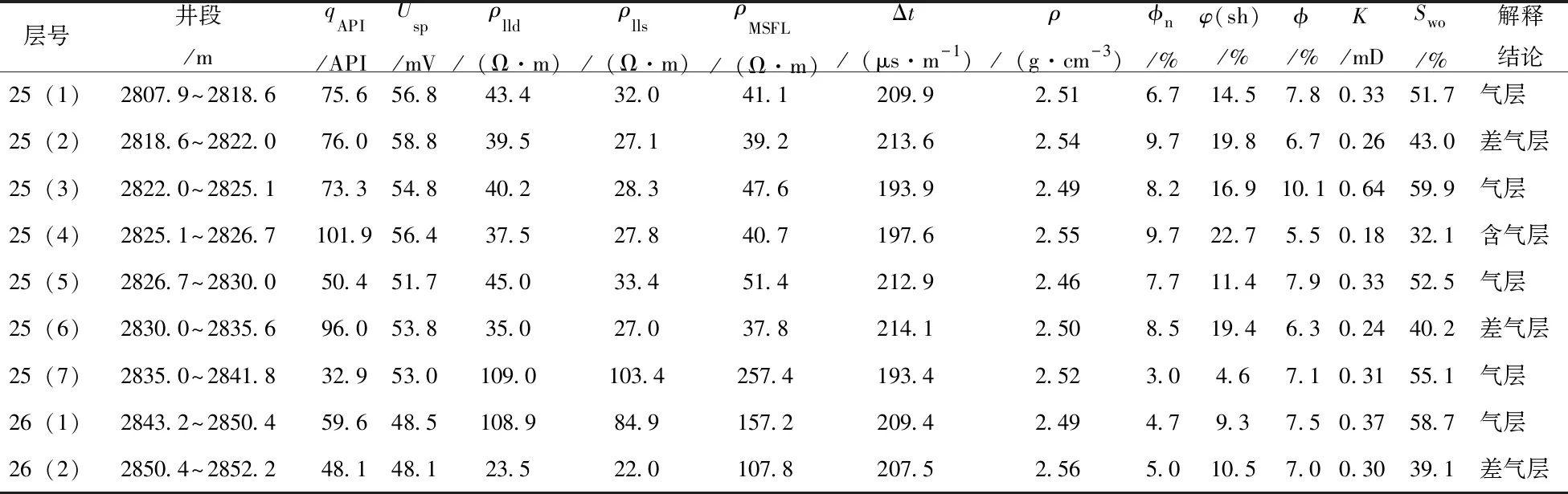
表5 B井二次解释成果表
注:qAPI为自然伽马;Usp为自然电位;ρlls、ρlld分别为浅侧向电阻率、深侧向电阻率;ρMSFL为微球形聚焦电阻率;φn为中子孔隙度;Swo为原始含水饱和度。
4 结论
1)提出适合大牛地气田高自然伽马致密砂岩储层的泥质体积分数计算方法,即自然伽马-中子孔隙度联合法。
2)在确定不同岩性砂岩骨架取值的基础上,建立各层组岩石体积计算方法,优化出孔隙度的体积模型计算方法,进而建立渗透率参数解释模型。
3)根据岩电试验分析成果,确定岩电参数。结合地层水分析资料,分层组确定地层水电阻率,建立不同层组的流体解释标准,建立饱和度参数解释模型。
