高速公路基本路段饱和度与交通事故关系研究

吴晓峰 童刚 孔晨晨 张沛

1. 公安部交通管理科学研究所 2. 陕西省公安厅交警总队

引言

近年来，随着经济快速发展，机动车数量增加迅猛，高速公路交通事故频发，而目前对高速公路交通事故的研究集中在事故本身，例如分析事故原因、车辆安全性、环境等，从交通流角度来分析的研究还不多。本文基于交通流饱和度（即V/C，交通量与通行能力的比值）这个反映交通状况的重要参数来分析其与交通事故的关系，探讨交通负荷对交通事故的影响。

一、现有研究分析

国外研究交通量或V/C与事故率关系有正相关或U型关系，国内研究V/C与事故率主要为U形关系。由于国外在事故及通行能力计算等方面与我国有所不同，因此成果不适用我国实际情况；另外国内外都研究宏观交通量或V/C与事故率的关系，未研究短时交通流波动与事故发生的关系。因此本文基于国内交通流实际，从中观角度针对每起事故发生前短时交通饱和度进行分析，采用反映事故发生可能性的频率和概率做为对象进行研究。

二、研究对象与分析方法

（一）研究对象

本文采用对交通流运行具有重要意义的高速公路基本路段作为研究对象，如图1所示。

选择无锡交警支队高速一大队所辖沪宁高速公路（G2京沪高速、G42沪蓉高速无锡段）基本路段进行研究，路段位于平原，长度为45km，双向8车道，道路平直，车道宽3.75m，设计车速120km/h，道路条件为理想条件。以基本路段主线卡口作为起点，至下一个交织区或匝道为终点的路段作为分析对象。具体路段如表1所示。

?

（二）数据来源

1. 交通事故数据

交通事故数据来自无锡市交警支队事故系统，选择2019年1～6月发生在表1中基本路段的事故信息，并选择与交通量关系较大的车辆间相撞事故数据进行针对性分析。

2. 交通流数据

采用基本路段上主线卡口的过车数据，主要包括车道、方向、号牌号码等，时间段为事故对应的时间段。

（三）计算方法

1. 通行能力计算

本文采用实际机动车通行能力，选取的数据对应天气状况为良好，单向N条车道通行能力用下式计算：CP= CB·N·fW· fHV· fP， 式中：CP为 实际通行能力（辆/h）；CB为基本通行能力（pcu/h）；N是单向车道数；fW为车道宽度和侧向净空对通行能力的修正系数，车道宽3.75m，中央分隔带宽3m，两侧有紧急停车带，取fW= 0.97；fHV是交通组成修正系数；fP为驾驶人修正系数，此处取1；基本通行能力取2200 pcu/h/车道；N取4；fHV用下式计算：fHV= [1+PHV( EHV-1)]-1，式中，PHV为大型车交通量占总交通量的百分比（%）；EHV为大型车换算成小客车的车辆换算系数。

习主席指出，没有网络安全，就没有国家安全。网络安全关乎国计民生，更关乎战争胜负。未来战争，兵马未动，信息先行。信息化战争条件下，网络攻防行动更是贯穿整个战争的始末。新形势下，省军区系统在后备力量调整改革过程中，紧跟时代发展，挖掘地方信息科技潜力，组建民兵网络信息分队，在近几年一些重大活动安保行动中发挥了重要作用。目前，民兵网军这支新质新锐后备力量队伍虽然已经初步建成，但是仍然面临较多的问题和矛盾，需要进一步研究和规范。

2. 事故频率和概率计算

事故频率以V/C值进行统计，首先计算每个事故发生前15分钟（该时间段车辆能通过这些路段）的V/C值，然后对这些V/C值进行分组，落在不同组中的事故次数为该组事故频数，事故频数与事故总数比值为事故频率，用来表征事故出现次数的相对多少。事故频率F表示为：F = N/S，式中，N为分组事故频数，S为事故总数。

将事故发生前15分钟V/C频数与所有V/C频数之比作为该V/C值发生事故的概率，记为P。P表示为：P = N/M，式中，N为分组事故频数，M为分组V/C总频数。

三、数据分析

（一）事故频率分析

通过对四条高速公路基本路段的事故频率和V/C值进行计算，并采用Gauss模型进行曲线拟合，得出分析结果如图2所示，可以看出V/C值与事故频率总体呈正态分布，拟合相关系数R2为0.9，并可以得出w为0.38，中心点xc对应的V/C值为0.67，在该V/C值下事故频率最高。

可以看出，事故频率处于高位的主要区间集中分布在xc-w/2（0.48）至xc+w/2（0.86）（落在该区间概率为68%），是事故频率正态分布的基区（主体和重点）。此外xc-1.96＊w/2至xc+1.96＊w/2（概率为95%）和xc-2.58＊w/2至xc+2.58＊w/2（概率为99%）则包含负区和正区。

需指出的是，当V/C小于xc-2.58＊w/2=0.2（如图3中红圈部分所示）时，V/C从不足0.1至0.2，事故频率有一个明显下降过程；而当V/C大于xc+2.58＊w/2=1.1时，事故频率快速降低至较低位置，直至趋于0。以下从安全角度分析交通流状态演变与V/C及事故频率关系，如图4所示。

1. 自由流状态（A-B段）

当V/C很小时，车辆间距大、干扰小、车速高，受行车视距、易疲劳时段等影响遇到异常情况时容易发生交通事故，随着交通量增长，V/C开始增大，车辆间距变小并开始有干扰，车速降低，驾驶人警惕性增强，事故频率下降，但总体处于较低水平。

当交通量继续增大时，车辆开始出现跟随前车行驶情形，形成稳定车流，超车需求和可能性开始增加，但减少的车辆间距又增加了车辆碰撞机会，因此与超车有关的事故开始增加，事故频率较车流量小时有明显上升。

3. 不稳定流状态（C-D段）

交通量进一步增大，虽仍有超车空间，但空间实际上已经较小，车速快速降低，形成不稳定流，此时超车需求大量增加，冲突点也快速增多，事故频率快速增大。当车辆间距达到最不适合超车距离时，事故频率达到最高，此后随着车辆间距进一步减小已不太容易超车，冲突次数开始下降，事故频率也开始下降，但事故频率仍处于高位。

4. 饱和流状态（D-E段）

当交通量增加到使车辆的间距大大减小、难以超车时，形成饱和交通流。由于饱和交通流的平均车速低、密度大，车辆变道和超车的机会大大减少，事故频率快速降低。

5. 阻塞流状态（E-F段）

当交通量增加至产生交通阻塞时，车辆只能尾随前车缓慢前行，事故频率减少，车辆停止时事故频率趋于零。

（二）事故概率分析

根据事故概率的计算方法统计指定时间段的事故概率分布，如图5所示。

由图5可以看出，事故概率的分布趋势特征与事故频率相似，在V/C值在0.2左右时，事故概率先是呈下降趋势，此时处于自由流状态，当V/C值逐渐增大时，事故概率呈上升趋势，V/C值未到0.5左右时，事故概率总体较小，当V/C值从0.5开始事故概率快速上升，至0.7时事故概率最高，然后开始下降，至0.9时仍处于高位，但当V/C值超过0.9时，事故概率呈快速下降趋势，当超过1.2时，事故概率趋于0，事故概率与频率的区间分布基本保持一致。

（三）结果分析

将本文研究结果与吉小进等人“高速公路基本路段V/C比与事故率的关系”研究成果（以下简称为“原成果”）进行比较分析，原成果“V/C与事故率呈U形关系，V/C为0.68时事故率最低”与本文“V/C与事故频率呈正态分布关系，V/C为0.67时事故频率最高”结论不一致，分析原因主要为：（1）统计对象差异。原成果V/C中通行能力采用计算出的某固定值，非动态值，而本文采用事故发生前交通量与当时通行能力之比；原成果采用的事故率是宏观数据，而本文采用的事故频率基于事故发生前饱和度和相应事故发生次数，是中观数据。（2）统计方式差异。原成果V/C采用一天24小时交通量与通行能力之比，事故率按年交通量和年交通事故再换算到小时进行计算，而本文采用事故发生前短时饱和度，事故频率为基于该短时饱和度的频率分布。

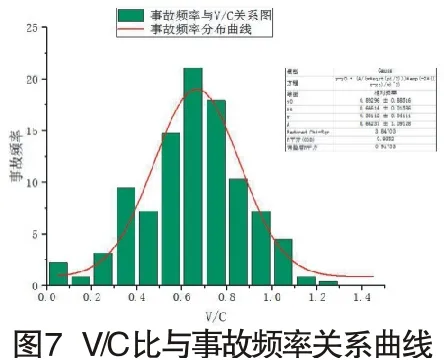
另外，从图6（原成果）、图7（本文）的结论图可以看出，原成果数据总体变化平稳，拟合度不高，也因源数据较为宏观，而本文数据变化趋势性更显著，具有较强针对性。

（四）方法应用

以G2京沪高速苏州交界处（由东向西）基本路段为例，笔者分别统计了各时段的大车、小车交通量，计算了V/C值，得出结果如图8所示。

相应的，笔者对一天24小时的大小车交通量和大小车比例分布进行了统计，如图9和图10所示。

可以看出，0时至7时大车比例相对较高，且存在较大的波动，范围为0.14至0.22之间，该时间段小车交通量在1500辆/小时以下，8时开始大车比例开始下降至0.1，至21时大车比例处于较稳定状态，维持在0.11至0.14之间，针对关注的9至11时、16至18时段，大车比例范围为0.11至0.12之间，取均值0.115，然后取V/C值0.67代入V/C值计算公式，得出大车交通量约为475辆/小时，小车交通量约为3665辆/小时。

四、结语

本文利用沪宁高速公路部分路段事故和交通流数据，计算V/C值和相应事故频率和概率，拟合出关系曲线模型，得出当V/C值为0.67时事故频率达到最高，分析出事故频率较高的V/C分布区间为0.48至0.86，事故概率与事故频率特征一致。需指出，本文得出的“V/C值为0.67时事故频率达到最高”等结论是基于沪宁高速公路四条基本路段，不具有普适性，其他高速公路可采用本文技术方法进行计算分析获取相应结果。本文研究成果可作为交通事故预防的一项分析指标，为交通管理部门制定安全管控措施提供有益参考。