桥架定型弯通满足电力电缆合规敷设相关参数研究

江期洪

(中铁建设集团有限公司 北京 100040)

1 引言

桥架作为电力电缆敷设的常用载体被广泛应用于建筑电气工程中，在桥架改变路由、改变位置的部位会设置不同的桥架定型弯通[1]，以满足桥架的连接通畅。桥架作为电力电缆的载体需要满足几大功能：(1)满足电力电缆承载要求；(2)满足电力电缆的合规通过，其中包括截面和弯曲半径要求；(3)提供对电力电缆的机械及防火保护。

本文针对桥架定型弯通满足电力电缆合规敷设的相关参数展开分析及计算研究，以期能对桥架定型弯通的工程设计和施工应用提供研究依据和帮助。

2 电力电缆敷设和桥架选择的规范依据

《电缆线路施工及验收规范》[2]第5.1.7条对电缆的最小弯曲半径有明确的规定，见表1；《低压配电设计规范》[3]第7.6.14条：“电缆在托盘和梯架内敷设时，电缆总截面积与托盘和梯架横断面面积之比，电力电缆不应大于40%，控制电缆应不大于50%”；《电缆线路施工及验收规范》第4.2.8条：“电缆桥架转弯处的转弯半径，应不小于该桥架上的电缆最小允许弯曲半径的最大者”；《电力工程电缆设计标准》[4]第5.1.4(3)条：“除交流系统用单芯电缆情况外，电力电缆相互间宜有1倍电缆外径的空隙”；《民用建筑电气设计规范》[5]第8.12.7条：“在电缆托盘上可以无间距敷设电缆，电缆在托盘内横断面的填充率，电力电缆应不大于40%，控制电缆应不大于50%”。

表1 电缆最小弯曲半径(常用电缆类型节选)

在桥架选型阶段，按照规范规定，首先根据敷设电缆数量、外径及间隙选择桥架的宽度和高度，然后复核电缆总截面与桥架横截面面积比是否满足要求，如果不满足需进行调整并重新复核。但按此条件选择的桥架是否能满足电力电缆通过桥架弯通时的电缆最小弯曲半径要求，目前国内还没有相关论述和研究。

工程中应用的各类桥架定型弯通都可以由水平弯通和竖向弯通两种基本型衍生组合出来，因此首选水平弯通和竖向弯通开展研究。

3 桥架水平定型弯通满足电缆合规通过的参数分析及数学模型

为突出主要研究对象，在分析前做以下合理约定：(1)电缆单层排布；(2)弯曲后电缆外径d和直线状态下外径一致；(3)电缆之间在最不利点处间隙为δ；(4)电缆均按90°转角过弯，直线段桥架内电缆的敷设排列应顺直、整齐[6]，不拧绞，见图1。

不规范的电缆敷设方式不在本文研究范围，过度的弯曲会折伤电缆[7]。

3.1 桥架水平定型弯通的相关参数

图1中的标注方法为目前国内桥架厂家常见的尺寸标注方式[8]，其中L为水平弯通长度，b为桥架宽度。但仅靠这两项参数无法确定W值，W是影响水平定型弯通电缆通过能力的重要参数，将其标注为桥架弯通的弯曲宽度。

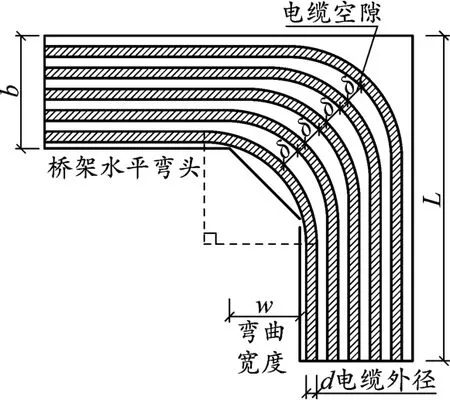
图1 规范的电缆敷设方式

3.2 单根电缆通过水平定型弯通分析

电缆最小允许弯曲半径Rmin可根据电缆类型按照式1确定。

式中，d为电缆实际外径；t为规范允许电缆最小弯曲倍数，按电缆类型查询表1确定。

如果Rmin≤W，电缆从内侧紧贴桥架侧边弯曲敷设即满足要求(见图2a)，此时弯通的W值对电缆过弯能力无任何限制；如果Rmin＞W，电缆最靠近内侧的过弯状态如图2b，此时电缆过弯后与桥架直线段内侧有一间隙，此间隙大小由W值和Rmin值决定，W值对电缆过弯有限制。

图2 单根电缆过弯分析

随着d值增大Rmin值也增大，单根电缆过弯的最大极限状态见图3。此时桥架水平弯通只能合规通过单根电缆，d值达到允许最大值dmax。

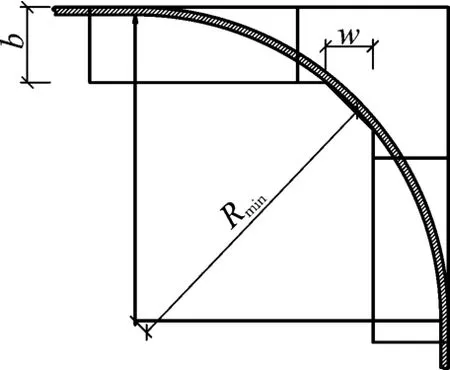
图3 单根电缆过弯极限状态(Rmin达到最大)

通过图3分析计算，可推导出以下公式：

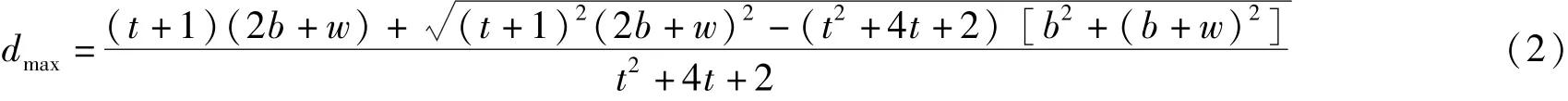
式中，dmax为合规通过最大电缆外径。从公式可以看出，针对特定的电缆，t是固定值，则dmax的大小取决于b和w，且随着b和w值的增大dmax也随之增大。

3.3 多根电缆通过水平定型弯通现状分析

根据单根电缆的理论分析，越粗的电缆布置在弯通弯曲外侧，越细的电缆布置在弯曲内侧，能在满足电缆弯曲半径要求的条件下最大限度利用桥架空间。

工程实际情况是电缆的数量、选型、截面和排布由配电设计决定，电缆敷设路由要根据其起始和终端在整个配电系统的走向合理布置，尽量排列整齐并减少交叉[9]。因此实际工程中不可能单纯按照电缆的外径来进行电缆优化排布，而是需要根据电缆的配电路由最佳排布来确定桥架定型弯通的合适参数。根据本文第2章节分析，设计通过电缆选型和截面明确桥架尺寸(包括宽度和高度)，因此桥架定型弯通的b值已经确定。目前所缺的是对定型弯通W值的研究，一方面不能判断能合规通过直线段的电缆排布是否能合规通过定型弯通；另一方面也没有针对给定的电缆排布，计算出能满足合规通过定型弯通最小W值的方法。

3.4 桥架水平定型弯通满足电缆合规通过的数学模型

基于前述分析，本文建立了一种数学模型和分析方法，能够针对给定的电缆排布利用迭代分析法解决以上两个问题。

已知电缆的类型t(可确定)、外径d、数量N、排布、水平定型弯通的b值、在过弯最不利点(弯通中轴线上)的电缆预留间隙值δ(自行设定合理值)及电缆规范允许最小弯曲半径Rmin。

从桥架弯曲内侧的第1根电缆开始，由内向外分析计算，找出每1根电缆的实际最优排布弯曲半径R，保证其既满足不小于Rmin，又能保证整体的电缆排布(包括电缆间隙)占用桥架宽度最小。

首先根据实际情况合理设定W初始值。

(1)步骤1：首根电缆R1与α1的确定

针对弯曲内侧的第1根电缆，根据单根电缆过弯的原理分析，可针对电缆外径的不同取值范围分成以下三种情况，得出电缆的R1与α1(第1根电缆与桥架内侧的间隙值)。

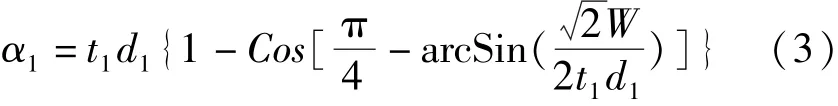
③如d1＞dmax(按公式2计算)，该W值下不能通过1根电缆，W值需要调大。

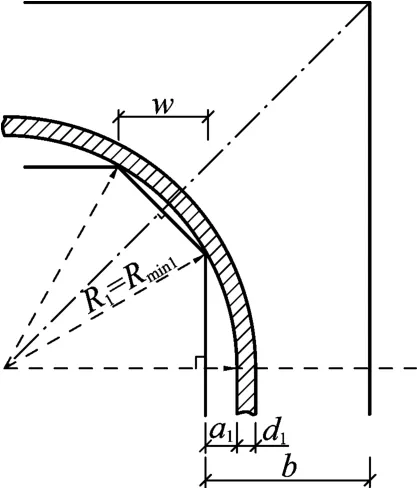
图4 首根电缆计算简图

(2)步骤 2：第 2根电缆R2与α2的确定

①针对第2根电缆，比较其Rmin2值与第1根电缆R1+d1+δ1值的大小。

如Rmin2≤(R1+d1+δ1)，则第2根电缆R2=R1+d1+δ1，α2=δ1( 见 图5a)；如Rmin2＞(R1+d1+δ1)，则第2根电缆在保证最不利点δ1值的基础上采用Rmin2值过弯，此时第2根电缆R2=Rmin2，见图5b。

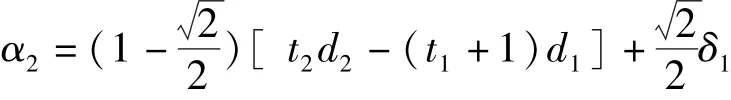
②比较(d1+d2+α1+α2)与桥架宽度b值大小，如(d1+d2+α1+α2)≤b，则：

如电缆设定数量大于2，进入下一步，如电缆设定数量为2，判定该W值能满足电缆合规过弯，且有b-(d1+d2+α1+α2)的余量；如(d1+d2+α1+α2) ＞b，则该W值不能满足电缆合规过弯，W值需重设。

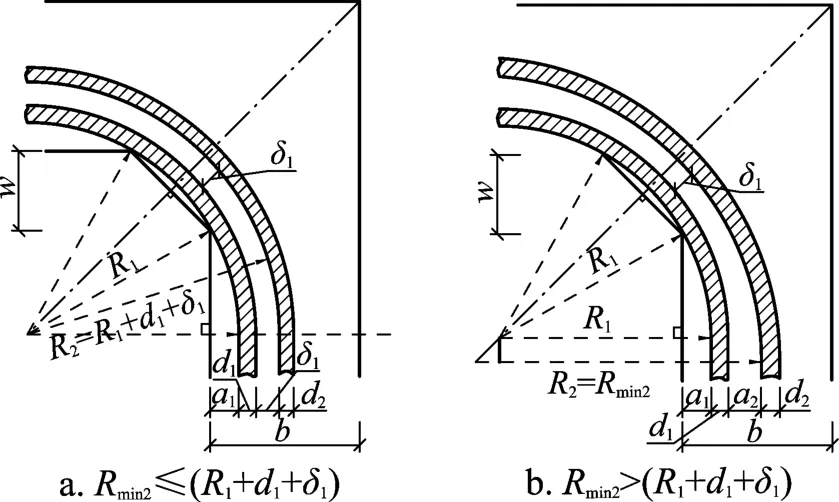
图5 第2根电缆计算简图

(3)步骤n：参数计算(n≥2，n为已知的电缆数量)

同第2步方法，针对第n根电缆不断进行迭代分析，最后计算出αn值。

①针对第n根电缆，比较其Rminn值与第n-1根电缆Rn-1+dn-1+δn-1值的大小，如Rminn≤(Rn-1+dn-1+δn-1)，则第n根电缆Rn=Rn-1+dn-1+δn-1，αn=δn-1；如Rminn＞ (Rn-1+dn-1+δn-1)，则第n根电缆采用Rminn值过弯，Rn=Rminn。

如当前n值未达到设定电缆数量N，进入下一步，如当前n值已达到设定电缆数量N，则判定该W值能满足电缆合规过弯，且有的余量；如＞b则该W值不能满足电缆合规过弯，W值需重新设定。

通过以上数学模型分析，针对任何给定电缆排布，设定一个W值即可得出该W值能否满足电缆合规过弯的结论，同时也能获得余量参数。利用该数学模型再结合数学迭代分析，应用软件编写计算程序[11]，能针对给定电缆排布和桥架宽度自动计算出满足电缆合规过弯的弯通最小W值(见图6)。

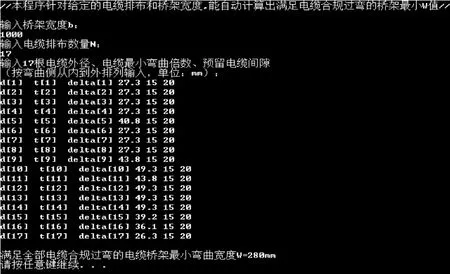
图6 利用软件分析计算桥架弯通最小W值

4 桥架竖向定型弯通满足电缆合规通过的相关参数研究

多根电缆通过竖向定型弯通的情况相对简单，此时桥架宽度和W值不在一个维度，只需考虑最不利情况，即单根最粗电缆能合规过弯，则其他电缆就都能满足。

将单根电缆通过水平定型弯通的水平弯通看做为竖向弯通，b值调整为h值，图3为竖向电缆过弯的极限状态，可推导出公式：

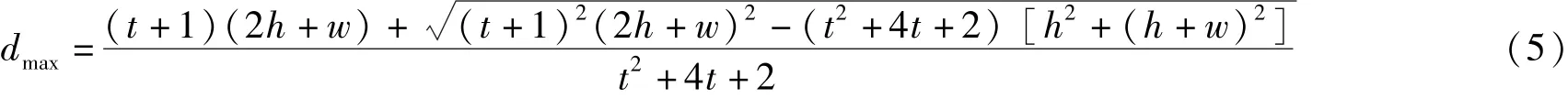
式中，dmax为合规通过最大电缆外径；t为电缆最小弯曲倍数；h为桥架高度；W为弯曲宽度。

dmax、h、w3个参数知道其中2个即可以求出第3个，dmax的值取决于h和w值的大小。

工程中其他桥架定型弯通都可以转化成水平弯通或竖向弯通的组合应用以上分析予以解决。

5 结束语

(1)对于确定类型的单根电缆，桥架水平定型弯通的电缆合规通过能力取决于桥架宽度b、弯曲宽度w参数。

(2)对于确定类型的多根电缆，桥架水平定型弯通的电缆合规通过能力取决于桥架宽度b、弯曲宽度w、电缆间最小间距δ、电缆排布等参数。

(3)通过本文建立的数学模型，能针对设计好的水平电缆排布方案和桥架定型弯通参数验算其是否能满足电缆合规过弯的要求；也能针对设计好的电缆排布方案和直线段桥架参数，给出桥架定型弯通满足电缆合规通过的最小弯曲宽度值。

(4)对于确定类型的电缆，桥架竖向定型弯通的电缆合规通过能力取决于桥架高度h、弯曲宽度w参数。可以通过其中最粗的电缆来验算电缆合规通过能力或求出桥架定型弯通满足电缆合规通过的最小弯曲宽度值。

(5)桥架定型弯通是整个桥架应用于电力电缆敷设中的薄弱环节。在实际工程桥架弯通选型定货前[12]，必须要验算桥架弯通的弯曲宽度值W能否满足电缆合规通过，尤其要重视变配电室、设备机房、强电竖井等大电缆敷设多且集中部位的桥架定型弯通W值的审核，如验算桥架厂家常规W值不能满足合规敷设要求，要根据验算结果要求厂家对W值予以调整，以确保电缆合规通过桥架定型弯通。