Numerical simulation of dynamic large deformation and fracture damage for solid armature in electromagnetic railgun
2020-05-23QinghuaLinBaomingLi
Qing-hua Lin, Bao-ming Li
National Key Laboratory of Transient Physics, Nanjing University of Science and Technology, P. O. Box, 210094, Nanjing, PR China
Keywords:Electromagnetic railgun Solid armature Fracture Explicit finite element Numerical simulation
ABSTRACT The design of solid armature of railgun should take full account of its operating conditions and material properties because the armature is subjected to dynamic loading conditions and experiences a complicated electrical, thermal and mechanical process in the interior ballistic cycle. In this paper present, we first introduced a multi-physical field model of railgun, followed by several examples to investigate the launching process. Especially, we used the explicit finite element method, in which material nonlinearity and geometric nonlinearity were accounted,to investigate the deform behaviors of solid armature. The results show that the dynamic mechanical process of armature is dependent on the armature geometry, material and exciting electric current. By the numerical simulation, the understanding of the fracture mechanism of solid armature was deepened.
1. Introduction
The electromagnetic railgun technology utilizes a high electric current of several mega-amperes to produce the Lorentz force and propel the projectile. Over the past few decades, researches have been focused mainly on the solid armature railgun that achieves the conversion from electric energy to kinetic energy by a sliding solid conductor [1].
Although the solid armature serves as a key component during the interior ballistic cycle,it is only a parasitic mass for the launch package. The solid armature should be as light as possible. However, over-light armature often has insufficient structural strength and is prone to large deformation or even fracture. Broken armatures were often seen in the high-speed videos of launching experiments. Moreover, the recovered armatures present severe distortion or fracture sometimes, as shown in Fig. 1. These phenomena suggest that the structure design was inappropriate, or that launching parameters exceed the armature's carrying capacity.
The large deformation and fracture inside the bore may lead to the failure of launching, even damage the bore materials and reduce the bore life. Moreover, the large deformation and fracture of the solid armature after it leaves the muzzle and before it is completely separated with the projectile, may disturb the flight of the projectile and increase its dispersion.Therefore,it is necessary to understand the deformation and fracture mechanisms of solid armature.
During the launching process of a railgun, the rail damage and armature damage are always associated. The mechanisms of rail damage including the gouging, grooving and arc transition have been researched extensively [2-5]. In the armature aspect, the melting and wear are the two major kinds of damage.F.Stefani[6-7]investigated the current melt-wave erosion of the solid armature and found that the armature contact surface experienced a fast heating and melting process. R. Merrill [8] proposed a turbulent melt-lubrication model to describe the surface wear of the armature. In addition, T. J. Watt [9-11] conducted experimental and computational investigations on the melting and cracking in the throat region of C-Shaped solid armatures. He attributed the armature damage to the magnetic saw effect.
Generally, it is thought that the armature damage is related to the material behaviors at the condition of rapid heating,high-speed impact and excessive force.In order to describe these details during the launching cycle, some computation software for railgun's multi-physical field were developed. D. Rodger [12] used the general 2D and 3D electromagnetic and heat transfer program (called MEGA)in some railgun simulations.Kuo-Ta Hsieh[13-14]analyzed the startup behavior in a “C-Shaped” armature using linked EMAP3D/DYNA3D finite element codes.H.Shatoff[15]developed a moving armature railgun code (called HERB) for coupled electromagnetic, thermal and structural fields using the general purpose code ANSYS as the underlying computational engine.Similar multiphysical field programs also included RGUN3D, EFFE, and others[16-19]. At present, LS-DYNA [20] is one of the few commercial software that have the capability to solve the railgun's coupled multi-physical field problem.

Fig.1. Photos of damaged armature.
Over the years we have been committed to develop the 3D transient multi-physical field model for railgun [21]. In order to make calculation more flexible in dealing with some key issues such as data exchange between fields,mesh deformation,element failure, contact and impact, we wrote a FORTRAN source code program for the coupled electromagnetic, thermal and structural fields. In this paper present, we utilized this multi-physical field solver to simulate the launching process, investigate the dynamic deformation behaviors, and explore the fracture damage mechanism of solid armature.
2. Models
The computation model is composed of three parts, which are the electromagnetic field model,thermal field model and structural field model. The computational regions of rails and armature are discretized by hexahedral elements,and each physical field shares the same mesh. The electromagnetic field is solved by the finiteelement/boundary-element coupling scheme, the thermal field is solved by the implicit finite element scheme, and the structural field is solved by the explicit finite element scheme. Furthermore,material nonlinearity is considered to model the complex mechanical behavior of solid armature.
2.1. Multi-physical field model
The electromagnetic field is described by the magnetic diffusion equations. With the assumptions that the thermal conductivity is isotropic and the railgun boundary is adiabatic, the thermal field model is simplified as a three-dimensional unsteady heat conduction problem. The ohmic heating source of thermal field is a function of the electric current density and electrical conductivity. The model of structural field is described by three equations,that is the mass conservation, momentum conservation and energy conservation, respectively. The Lorentz force density from the results of electromagnetic field is added to the structural field as body force.Detailed governing equations of the multi-physical field can be found in Ref. [21].
2.2. Material model
We chose the Johnson-cook material model [22]because it can not only account for the effects of elastic-plastic, temperature and strain rate,but also contains a damage model.
2.2.1. Constitutive equation
The yield stress is written as
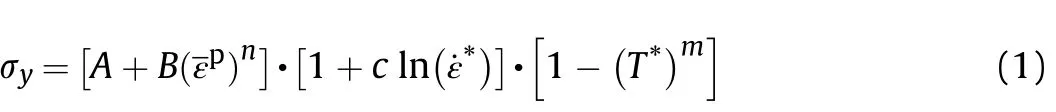
whereA,B,c,nandmare material constants,is the effective plastic strain,is the non-dimensional strain rate, andT* is the homologous temperature.
2.2.2. Damage model
The strain at fracture εfis given by
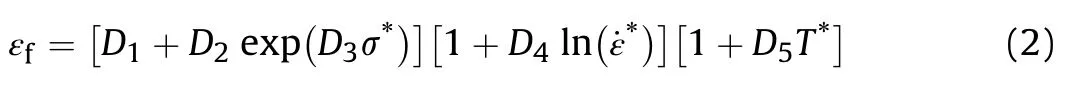
where,σ*is the ratio of pressure divided by effective stress,D1~D5are the damage parameters.
Fracture occurs when the damage parameterDexceeds the value of 1. The evolution of the damage parameter is given by

where the summation is performed over all time steps in the analysis.
2.2.3. Equation of state
The equation of state (EOS) is used to describe the relations of pressure,volume and internal energy.There are two EOS model in our computing program, which are linear polynomial model and Gruneisen model.
The linear polynomial EOS is linear in internal energy, the pressure is expressed as
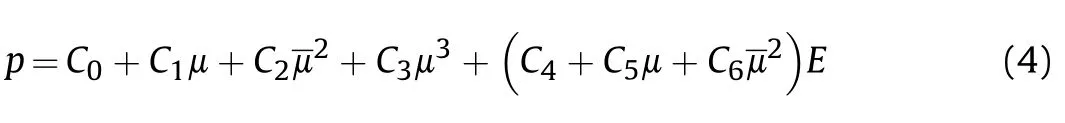
whereEis the internal energy,μ is the excess compression,andis the tension-limited excess compression. In our simulation, Eq. (4)served as the EOS for aluminum alloy 6061-T6, and the coefficients are:C0=0,C1=74.2 GPa,C2=60.5 GPa,C3=36.5 GPa,C4=1.97,C5=C6=0.
The Gruneisen EOS with cubic shock velocity-particle velocity defines pressure for compressed materials (μ > 0) as
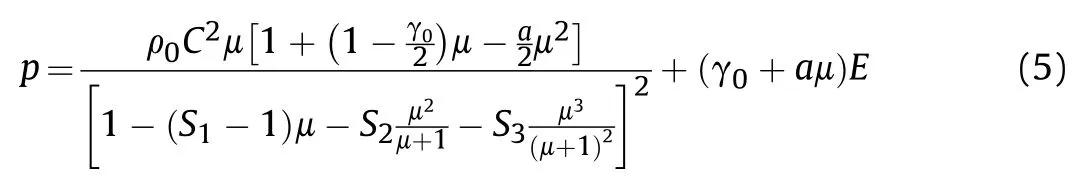
whereCis the intercept of the shock velocity vs. particle velocity(vs-vp)curve,S1,S2,andS3are the coefficients of the slope of thevsvpcurve, γ0is the Gruneisen coefficient, andais the first order volume correction to γ0.
In our simulation,Gruneisen model was used to aluminum alloy 7075-T6, and the parameters are: ρ0=2700 kg/m3,C=5386 m/s,S1=1.339,S2=S3=0,γ0=1.97,a=0.
The other material parameters of aluminum alloy 6061 and 7075 are listed in Tables 1 and 2 [23-25].

Table 1 Parameters of Johnson-cook strength model for Al 6061-T6 and 7075-T6.
3. Results and discussion
We conducted numerical simulations for the multi-physical fields of railgun. This section starts with a comparison of two examples with the same geometry and different material models.Then,the effects of exciting electric current,armature material,and railgun geometry on the deformation and fracture of armature were investigated.
3.1. Mechanical behaviors of armature with linear and nonlinear material model
The in-bore processes of a solid armature were calculated with the same model geometry, exciting electric current, as well as the different material models.The armature material is Al 6061,and the material models are elastic and Johnson-cook elastic-plastic respectively.In the elastic model,the Young's modulus is 68.9 GPa and the Poisson ratio is 0.33. The waveform of exciting electric current is the one labeled as “1.0” in Fig. 7.
We selected an element to plot its stress histories and a node to plot its displacements.As shown in Fig.2,the element is marked as H1,which is located at the throat of the C-shape armature.The node is located at the outer surface of the armature arm.The armature is of a length of 50 mm,a width of 50 mm,and a thickness of 30 mm.The rail is of a length of 3 m,a width of 56 mm, and a thickness of 20 mm.
Fig. 3 shows the stress histories of element H1. In the elastic example, the element stress reaches about 700 MPa at the time of 1.10 ms. Such high a stress is obviously impossible for real aluminum material. Moreover, the stress of elastic example presents an attenuated oscillation. The stress history of the elasticplastic example is quite different from that of the elastic one after 0.90 ms, and the magnitude of the elastic-plastic example before 0.90 ms is also lower than that of the elastic example.
The x-directional displacements of node N1 are plotted in Fig.4.This node experiences different dynamic processes after 0.90 ms.These two examples indicate that the material model plays a key role in the numerical simulation of dynamic launching process of railgun.
Besides the local mechanical behaviors,the material models also affect the motion behaviors of armature as a whole.Fig.5 shows the x-directional displacements of the armature's mass center. It is found that the armatures swing at the x direction, and their amplitudes present an increasing trend.
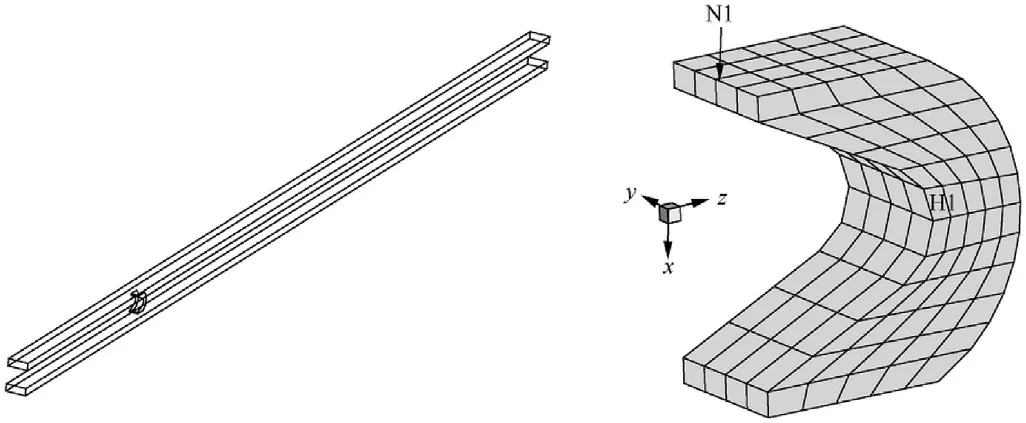
Fig. 2. Model of railgun and mesh of armature.
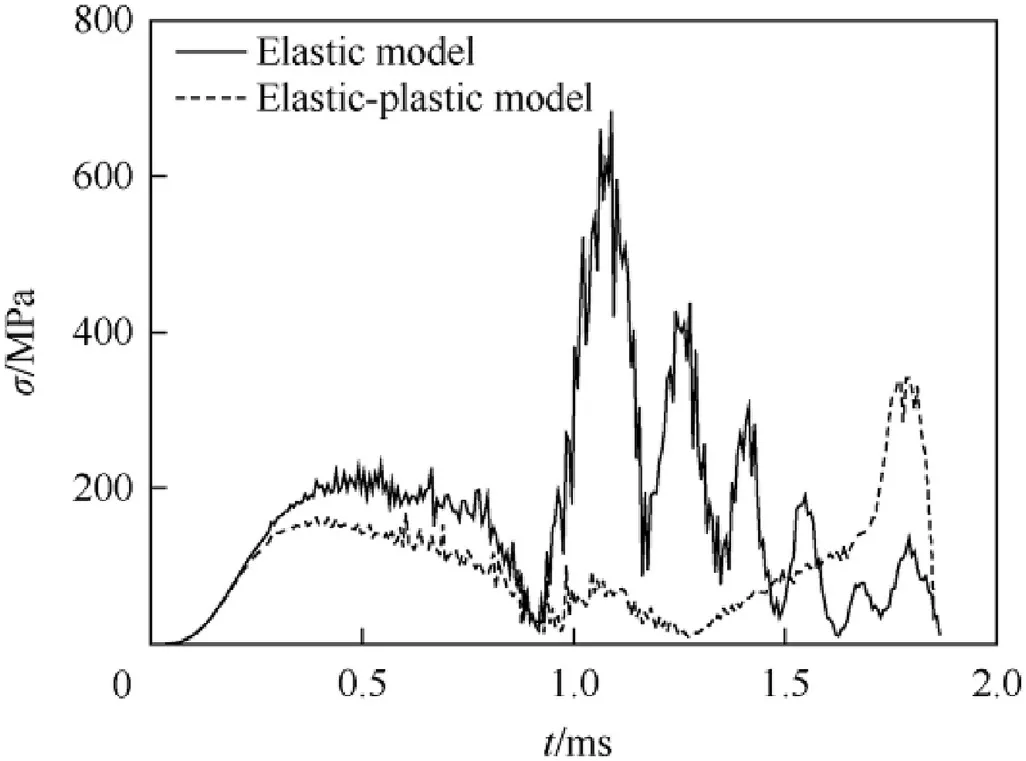
Fig. 3. Stress histories of element H1.
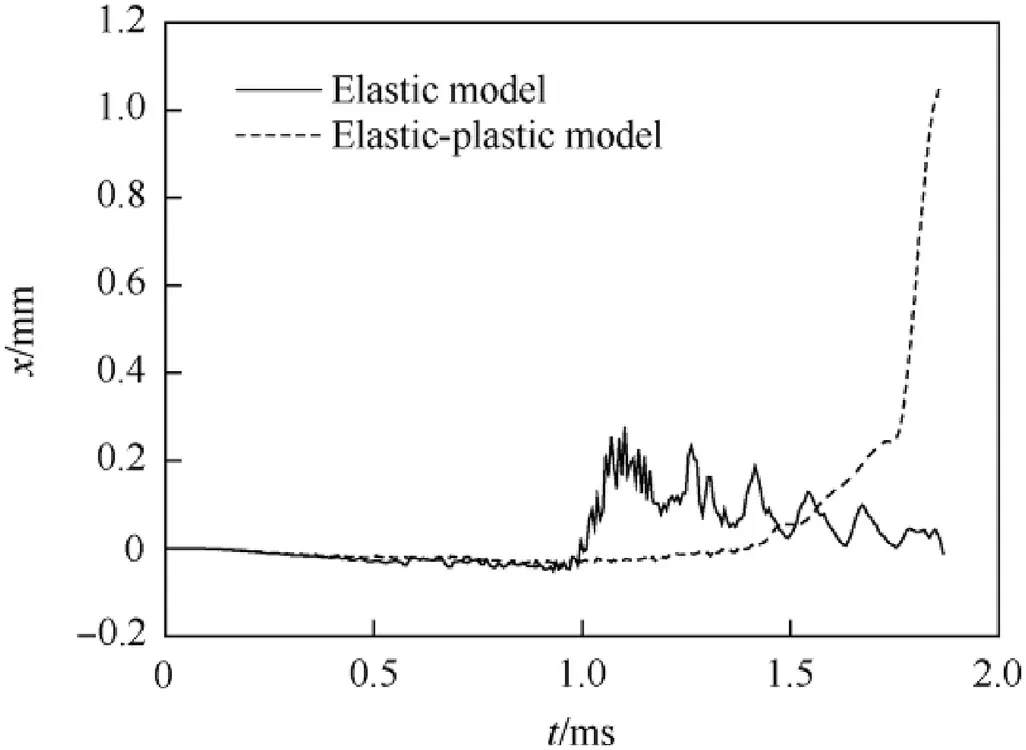
Fig. 4. Comparison of x-directional displacements of node N1.
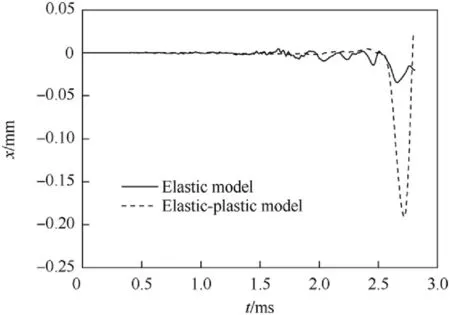
Fig. 5. Comparison of x-directional displacements of the armature's mass center.
It is well known that the dynamic response of the rails is induced by a moving magnetic pressure during launch of projectiles [26]. The deformation of rails acts directly on the armature through the rail-armature contact surface.Therefore,the local and global displacement fluctuations of armature are most likely caused by the rail deformation.Despite the different material models of armature, we found that the dynamic responses of rails were similar. Fig. 6 only shows the results of nonlinear material model case. The x-directional displacements of nodes at the centerline of the rail surface fluctuate during the launching cycle.Their amplitudes are smaller than that of the armature.
3.2. Deformation and fracture of armature at different exciting electric currents
Using the same model as Fig. 2, we calculated the launching processes with different electric current curves. Taken the bottom curve as the benchmark,the numbers in Fig.7 represent the fold of the magnitude of the electric current curve.
The armature is made of Al 6061-T6, and the material model is Johnson-cook.We carried out the calculation for two stages,which were the in-bore process and the free flight process of armature.
With the increase of electric current, we found that some elements successively failed outside the bore and inside the bore. In Fig.7,the muzzle time is marked by dotted line,the time of element failure inside the bore is labeled by the symbol“★”,and the time of element failure outside the bore is labeled by “·”. Fig. 7 indicates that the higher the electric current, the earlier the element failure occurs.
3.2.1. Deformation and fracture of armature outside bore
The motion of the armature was tracked after it was shot out the muzzle. For the example of 1.2-fold electric current, the time sequences of the armature shape are plotted in Fig. 8. It can be seen that the armature arms are experiencing an expanding and contracting process.The swings of arms may be related to the release of elastic strain energy at the situation that the constraint of the rails to the solid armature is abruptly removed.
In the example of 1.4-fold electric current,it was found that the armature fractured outside the bore.Fig.9 shows the process of the armature's deformation and fracture. The armature keeps normal shape when it just leaves the muzzle at 1.76 ms.Then,the armature arms expand outward and the armature is severely deformed.High stress region appears in the armature throat at 2.36 ms. Element failure occurs at 2.46 ms, and the armature fractures from the throat.
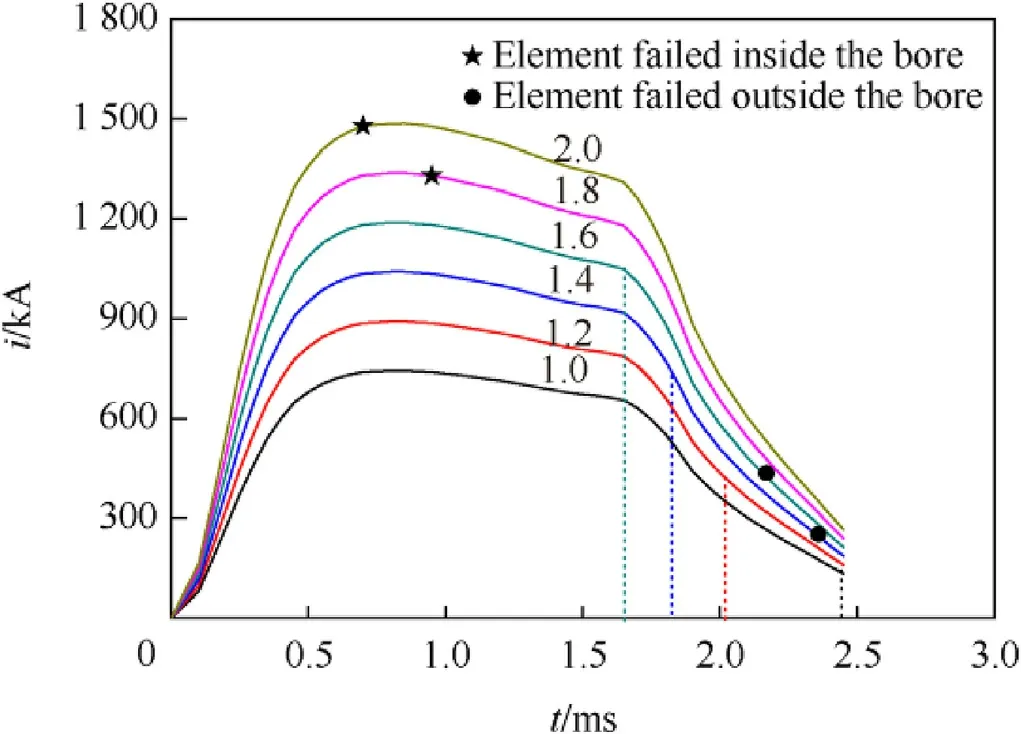
Fig. 7. Element failure time of Al 6061 armature at different electric currents.
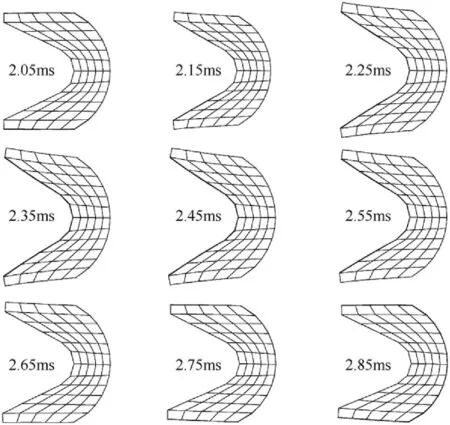
Fig. 8. Geometries of the armature after leaving the muzzle.
In reality,a high tensile stress at the throat of the armature due to the large deformation should cause cracks first,and then leads to fracture. Although the detailed generation and evolution of cracks can not be simulated by the finite element method, the fracture model based on the element failure can predict the location and condition of the damage. This is enough for armature design.
3.2.2. Deformation and element failure of armature inside the bore
When the armature was drove by the 1.8-fold electric current in Fig. 7, element failure occurred inside the bore. Stress contours of the armature are shown in Fig. 10. At 0.70 ms, the current curve reaches peak value.Although the maximum stress of the armature is 340 MPa and has exceeded the 6061's yield strength,there is no obvious deformation. At 0.95 ms, the stress at the armature throat reaches 420 MPa, large deformation appears and element failure occurs. The element fails latter than the peak-value time of the electric current curve, which suggests that the occurrence of armature damage has time effect. It is likely to be related to the histories of temperature rise and plastic deformation.
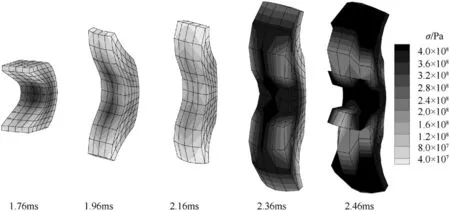
Fig. 9. Process of armature deformation and fracture.
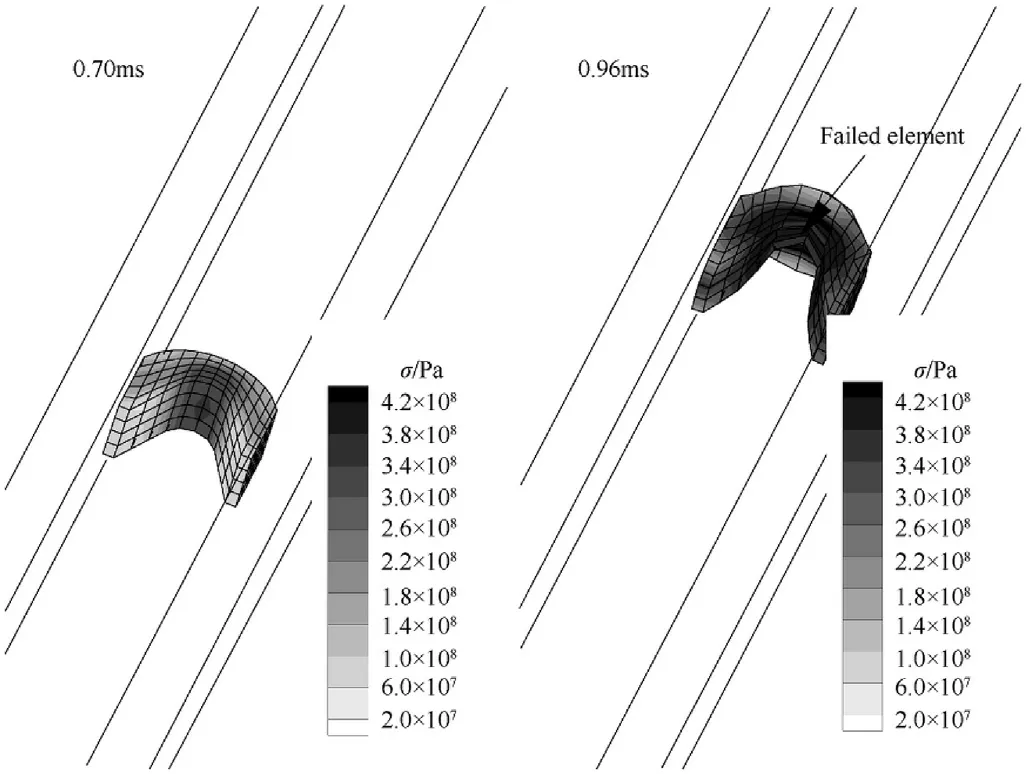
Fig.10. Stress contours of armature driven by the 1.8-fold electric current.
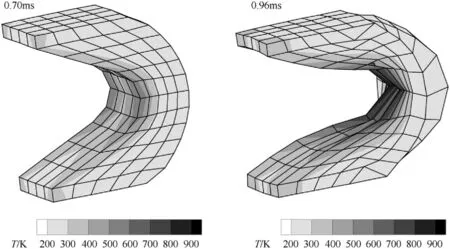
Fig.11. Temperature contours of armature driven by the 1.8-fold electric current.
In addition,it is found that when the armature is damaged,the stress is higher than the yield strength. This suggests that the armature can also work well within a certain range of plastic deformation.If the deformation of armature is only designed in the elastic range, the current carrying capacity of armature may be underestimated.
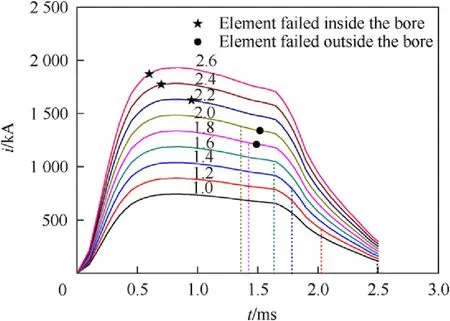
Fig.12. Element failure time of Al 7075 armature at different electric currents.
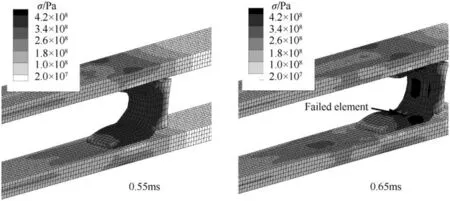
Fig.13. Stress contours of railgun with a different armature geometry.
Fig.11 shows the temperature contours at 0.70 ms and 0.96 ms.The temperature rises rapidly under the action of high electric current. The temperature of the armature throat at 0.96 ms has reached about 900 K,and is very close to the melting point listed in Table 1. At such a high temperature, occurrences of strength reduction and element failure are inevitable.
3.3. Effect of armature material
For the Al 7075, similar calculations as Fig. 7 were conducted.The time of element failure are shown in Fig. 12. It is found that 7075 is of higher current carrying capacity than 6061.This is due to the higher yield strength of Al 7075.
3.4. Effect of armature geometry
In above examples, all of the fractures occur at the throat of armature.Actually,the location of the fracture is also dependent on the armature geometry.As shown in Fig.13 in which the armature geometry is different, the element failure occurs at the root of the armature arm.
4. Conclusion
Some issues about the armature's deformation and fracture were investigated in this paper. The major conclusions were summarized as following:
(1) The large plastic deformation inside the bore and the release of elastic strain energy outside the bore are the two major mechanisms of armature fracture.
(2) The deformation and fracture of armature are affected by the material, geometry and exciting electric current.
(3) It is permissible for the armature to undergo a certain range of plastic deformation during the launching cycle.
The multi-physical fields modeling and simulation provided a deeper understanding on the armature's mechanical behavior.
杂志排行
Defence Technology的其它文章
- A comparison of the ballistic behaviour of conventionally sintered and additively manufactured alumina
- Effect of operating temperature on aged single lap bonded joints
- Investigation on energy output structure of explosives near-ground explosion
- Characteristics structure analysis on debris cloud in the hypervelocity impact of disk projectile on thin plate
- A fast-running method for blast load prediction shielding by a protective barrier
- Coating processes towards selective laser sintering of energetic material composites
