Hexapod多自由度微激励系统的振动时域波形控制

刘 璇，黄 海，郑 琰

0 引 言

由各种内外部因素造成的振动激扰源，导致在轨航天器不可避免地长期处于微振动状态[1].对高精度航天器而言，这种量级为mg的微振动环境效应仍会影响有效载荷的指向稳定性、成像质量、姿态稳定度[2-3].且实际振动环境大部分是多轴向的[4].对此，王海强等研制了六自由度运动可控的Hexapod多自由度微激励系统[5]，以开展航天器有效载荷地面微振动环境试验.并提出高频自适应正弦振动控制方法[6]，实现了20～300 Hz加速度正弦定频和扫频振动控制，时域误差小于10%.但采用此方法，从20 Hz逆向正弦扫频，14.5 Hz之后响应波动变大，并最终在13.5 Hz发散.故周世骥提出了基于位移反馈的自适应正弦振动控制[7]跟踪5～15 Hz低频加速度，但时域误差大于30%.根据遥感系列卫星力学环境测量数据[8-9]得知，微振动的类型主要为正弦，频率范围为零点几赫兹至几百赫兹.因此，为使得Hexapod多自由度微激励系统能对低频微振动工况进行高精度模拟，有必要研究快速精确稳定跟踪低频定频正弦加速度的控制方法.

振动试验系统采用的自适应逆控制、幅值相位控制等基于最小均方(LMS)自适应滤波器的控制方法，当被控对象相位滞后较大时，控制过程中超调和震荡严重，最终导致控制发散[10].这也是现有高频自适应控制方法无法稳定精确跟踪低频正弦加速度的原因，而基于位移反馈的自适应正弦振动控制的精度较低，还是应直接对加速度进行控制.离线迭代控制就具有对非最小相位系统或延迟系统进行稳定补偿控制的优点[11-12].它是一种基于频域逆模型的前馈控制，由Cryer[13]提出，并应用于四通道道路仿真器的时域波形跟踪，不过需要多次迭代使得输出信号满足精度要求，较耗时[14].所以，加快离线迭代控制的收敛，能更好地发挥离线迭代的优势，改善低频波形跟踪性能.

为加快离线迭代控制的收敛，改善波形跟踪性能，国内外研究者主要从以下两个方面提出多种改进方法.一方面提高阻抗矩阵的精度，Cornelis[15]针对弱耦合多轴液压振动台，采用优化的激励信号提高辨识精度和自适应建模更新阻抗矩阵.杨志东等[16]应用准牛顿优化算法修正系统阻抗函数，实现单轴液压振动台正弦扫频.另一方面引入实时反馈控制，Cuyper[17]提出基于离线迭代控制和H∞反馈控制器的复合控制方法，对单轴振动台开展了验证实验，但设计多输入多输出系统的反馈控制器太复杂，不适用.Tang等[18]提出复合改进内模控制的离线迭代控制，改善了液压地震模拟振动台的波形跟踪性能.在以上文献中，所提的改进方法都只局限适用于弱耦合或非耦合系统，当前未针对强耦合、非线性在部分频段较强的振动试验系统提出改进方法，并进行实验验证.

基于此，要实现强耦合、非线性在低频段较强的Hexapod多自由度微激励系统的低频振动时域波形控制，快速高精度跟踪低频定频正弦加速度，本文基于传统离线迭代控制方法，结合激励系统低频段特性，提出一种复合超前校正、多倍频陷波滤波器的改进离线迭代控制方法，并证明该方法的收敛性质.最后，基于激励系统，进行多组低频定频正弦加速度跟踪实验，对比传统离线迭代控制方法，验证该改进方法具有收敛快、控制精度高的优越性，对比自适应正弦振动控制方法，验证该改进方法能扩宽符合精度要求的加速度控制频带下限.

1 微激励系统控制问题描述

Hexapod多自由度微激励系统包括振动台机械系统、工业控制计算机、功率放大器、控制器软件等.其中，Hexapod构型振动台如图1所示.

图1 Hexapod构型振动台

该振动台由上下平台、音圈电机作动腿、虎克铰、空气弹簧以及辅助支撑组成.采用6-PUS六杆并联机构，下平台固定，通过6个杆/腿的伸缩运动，上平台产生可控的三维空间线位移和角位移运动，加速度传感器布置在上平台，位移传感器安装于各作动腿.

图2为现有基于Hexapod多自由度微激励系统的高频自适应正弦振动控制方法[6](accADC)，是一种实时前馈控制.借助系统辨识获得系统逆模型Z(f),并串联此逆模型实现解耦，然后基于自适应控制器，完成对广义控制对象H(f)Z(f)的加速度振动控制.

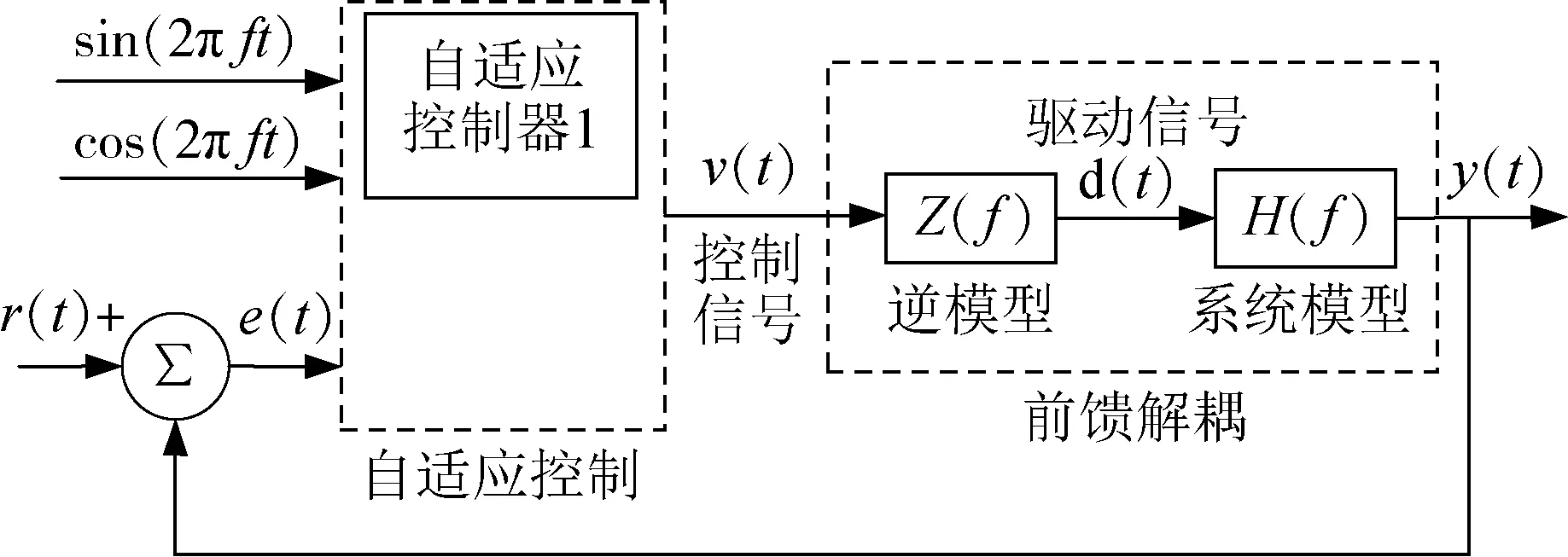
图2 高频自适应正弦振动控制

(1)

式中，I6为六维单位矩阵.

那么，广义被控对象存在如下关系:

H(f)Z(f)=I6+ΔH(f)

(2)

采用上述高频自适应正弦振动控制方法，以20 Hz为起点，逆向扫频，X向正弦扫频响应信号如图3所示.由图3可知，14.5～20 Hz控制精度高，响应的幅值误差范围在1～2 mg，时域误差小于20%，满足精度要求.14.5 Hz之后响应波动剧烈，超调严重.由频率范围为13.93～13.95 Hz的响应放大图也可知，随着频率减小，响应不断变大，误差也不断变大.自适应控制变得不稳定，并最终在13.5 Hz发散，无法继续稳定精确地跟踪低频正弦加速度信号.此时，满足精度要求的加速度控制频带下限为14.5 Hz.

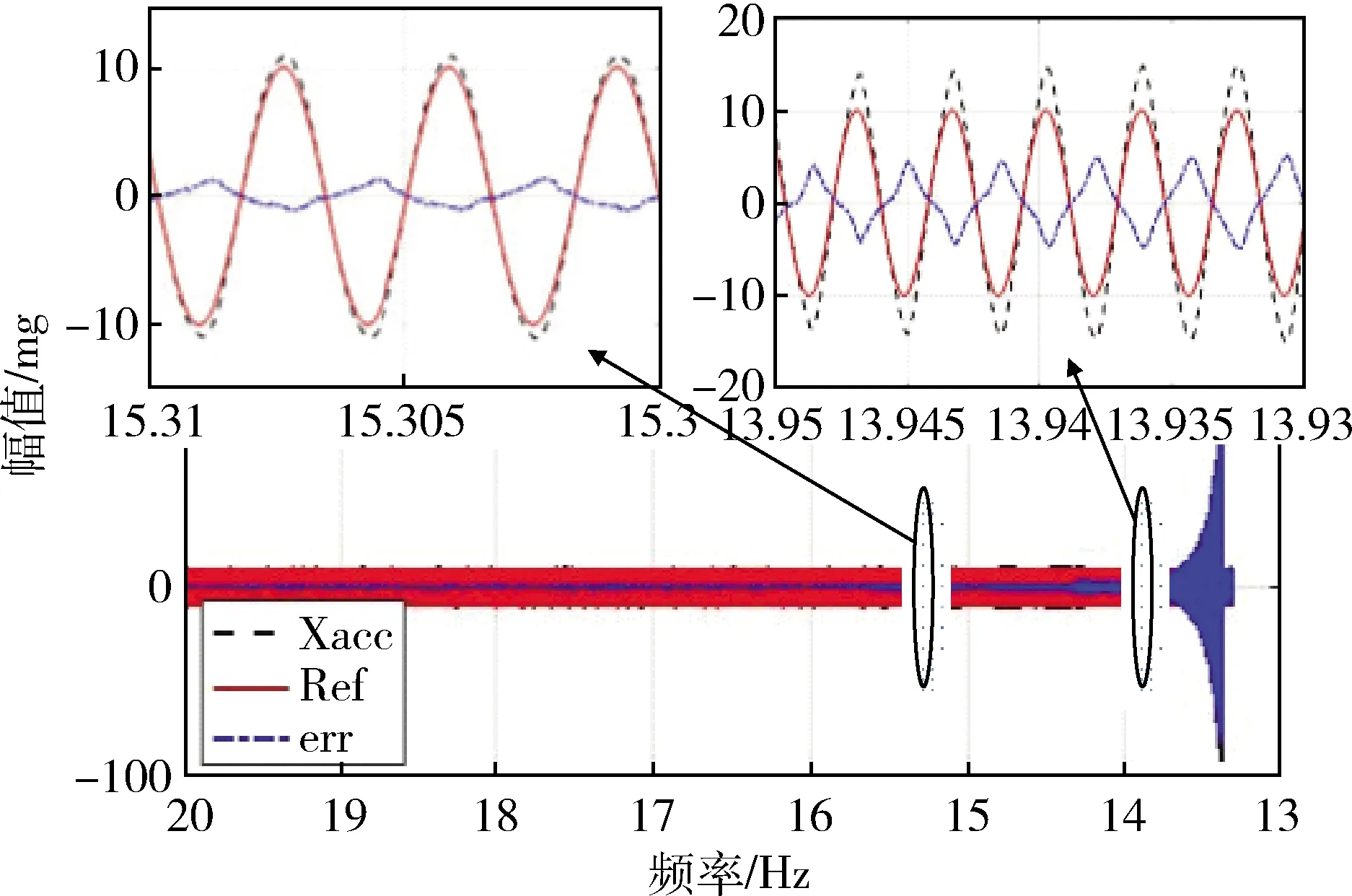
图3 X向逆向正弦扫频响应信号

从而采用图4基于位移反馈的自适应正弦振动控制方法[7]继续跟踪低频加速度.上平台六自由度加速度期望信号位置反解得各作动腿位移指令r(t),然后基于自适应控制器和超前校正环节得到作动腿的驱动信号，完成微激励系统的位移振动控制，由加速度传感器采集数据获得各自由度的加速度响应.

考虑到加速度传感器的低频频响特性，采用该基于位移反馈的自适应正弦振动控制方法，正向正弦扫频跟踪5～15 Hz低频正弦加速度，X向加速度响应如图5所示.由图5中的放大图可知，响应的幅值误差大于3 mg，时域误差大于30%，不满足精度要求.这是因为正弦位移与加速度的换算关系与频率平方成正比，随着频率变化，较小的位移误差对应的加速度时域误差会被放大.另外，位置反解矩阵随着频率变化，也存在误差.所以直接控制加速度，才能保证高精度地跟踪低频加速度，这就需要研究多自由度微激励系统低频段的特性.

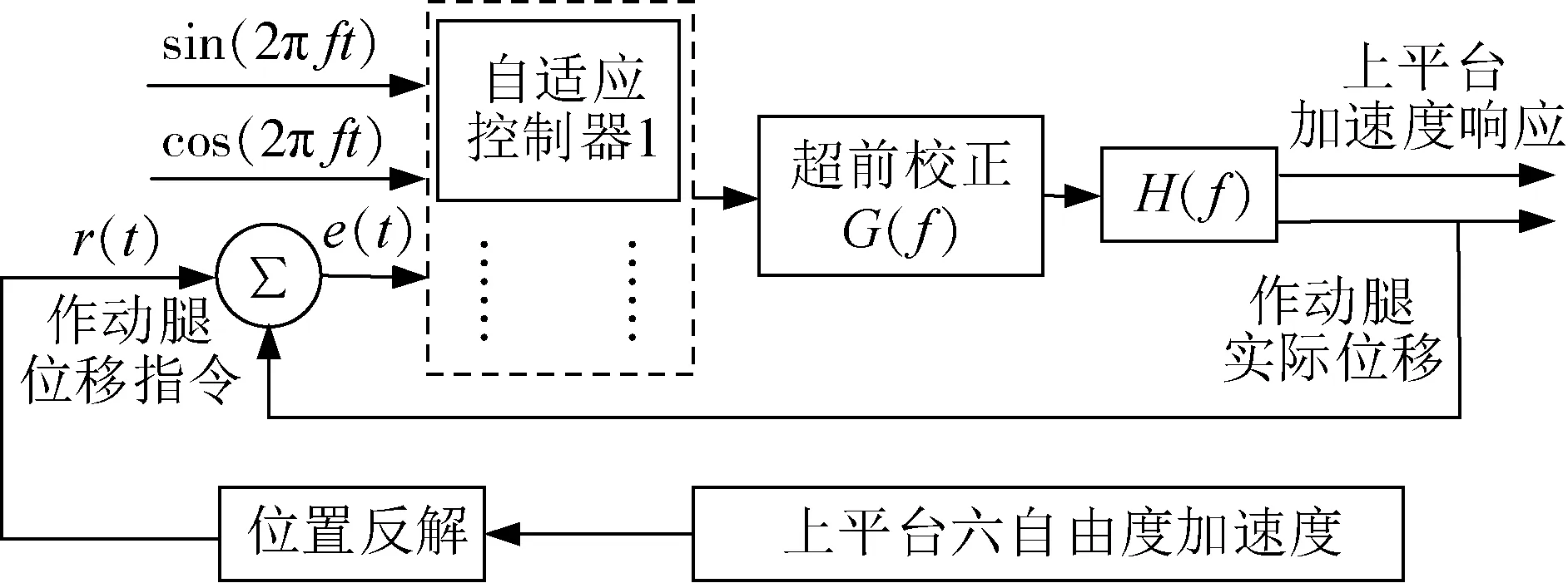
图4 基于位移反馈的自适应正弦振动控制

图5 X向正向正弦扫频响应信号

故从5～14.5 Hz频率段内选取多个频点，串联逆模型进行大量开环正弦振动实验，发现加速度响应均出现多倍频谐波和较大的相位滞后.因此，在这一低频段，Hexapod多自由度微激励系统具有较强的非线性，辨识模型只是实际系统模型的线性近似，模型误差造成响应出现相位滞后，即广义被控对象是一个相位延迟系统，最终导致高频自适应正弦振动控制方法发散，无法继续高精度稳定跟踪低频正弦加速度信号.

由于离线迭代控制方法可以进行非最小相位系统或延迟系统的补偿控制，且有很好的稳定性，这是自适应控制等实时前馈控制方法很难做到的.因此，基于离线迭代控制方法设计控制器，能实现快速高精度跟踪低频定频正弦加速度，完成Hexapod多自由度微激励系统的振动时域波形控制.

2 控制器设计

2.1 传统离线迭代控制

传统离线迭代控制的原理[17]如图6所示，实线表示实时控制，虚线表示离线控制.其中，R(f)为正弦加速度目标信号向量，Dk(f)为第k次迭代的驱动信号向量，Ek(f)为第k次迭代的误差信号向量，Yk(f)为第k次迭代的加速度响应信号向量，Dk+1(f)为第k+1次迭代的驱动信号向量，Yk+1(f)为第k+1次迭代的加速度响应信号向量，ΔDk(f)为第k+1次迭代的修正信号向量.

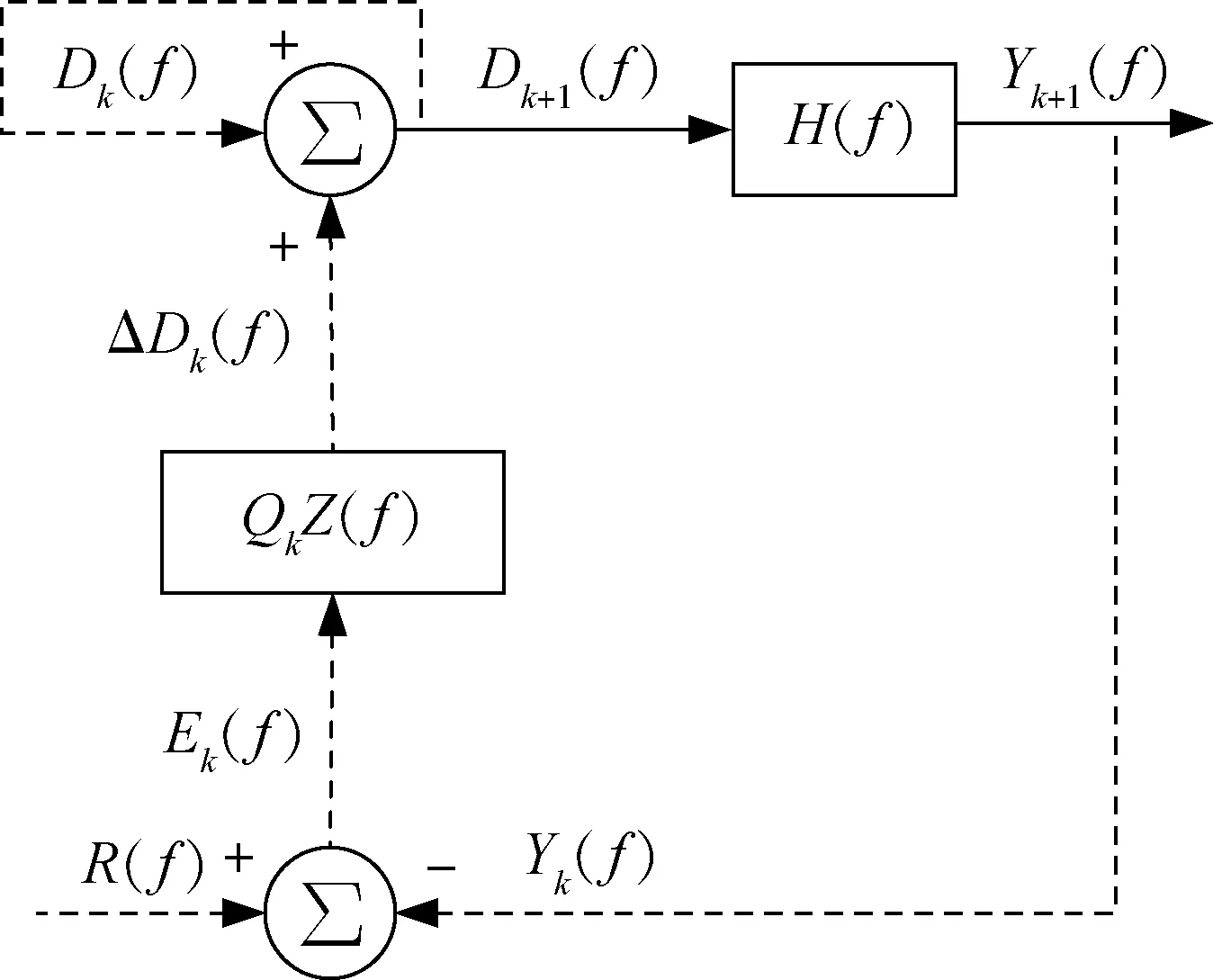
图6 传统离线迭代控制原理图

驱动信号更新公式为

Dk+1(f)=Dk(f)+ΔDk(f)

=Dk(f)+QkZ(f)Ek(f)

(3)

Qk对角线上所有元素相等，即Qk=αkI.其中，αk为迭代增益.则式(3)简化为

Dk+1(f)=Dk(f)+αkZ(f)Ek(f)

(4)

将第k+1次驱动信号输入给系统，误差信号为

Ek+1(f)=R(f)-Yk+1(f)=R(f)-H(f)Dk+1(f)

(5)

将式(2)、式(4)代入式(5)，可得

Ek+1(f)=[I6-αk(I6+ΔH(f))]Ek(f)

(6)

离线迭代控制收敛，则要满足

‖I6-αk(I6+ΔH(f)‖<1

(7)

2.2 改进离线迭代控制

Hexapod多自由度微激励系统耦合度高、非线性在低频段较强、被控对象相位滞后角过大，当采用传统离线迭代控制方法跟踪低频正弦加速度时，为保证收敛，一般选取小迭代增益，这就需多次迭代才能达到指定的控制精度，不仅耗时，而且可能破坏试验负载.因此，提出一种改进离线迭代控制方法，加快激励系统响应信号的相移补偿，从而加快低频振动控制的收敛，并改善低频波形跟踪性能，原理如图7所示.

图7中，基于传统离线迭代控制，对每个控制支路，串联相同的超前校正环节Gc补偿系统相位；串联相同的多倍频陷波滤波器Gd,衰减Dk+1(f)中的多倍频成分，去除Yk(f)中多倍频谐波引入的非线性干扰.

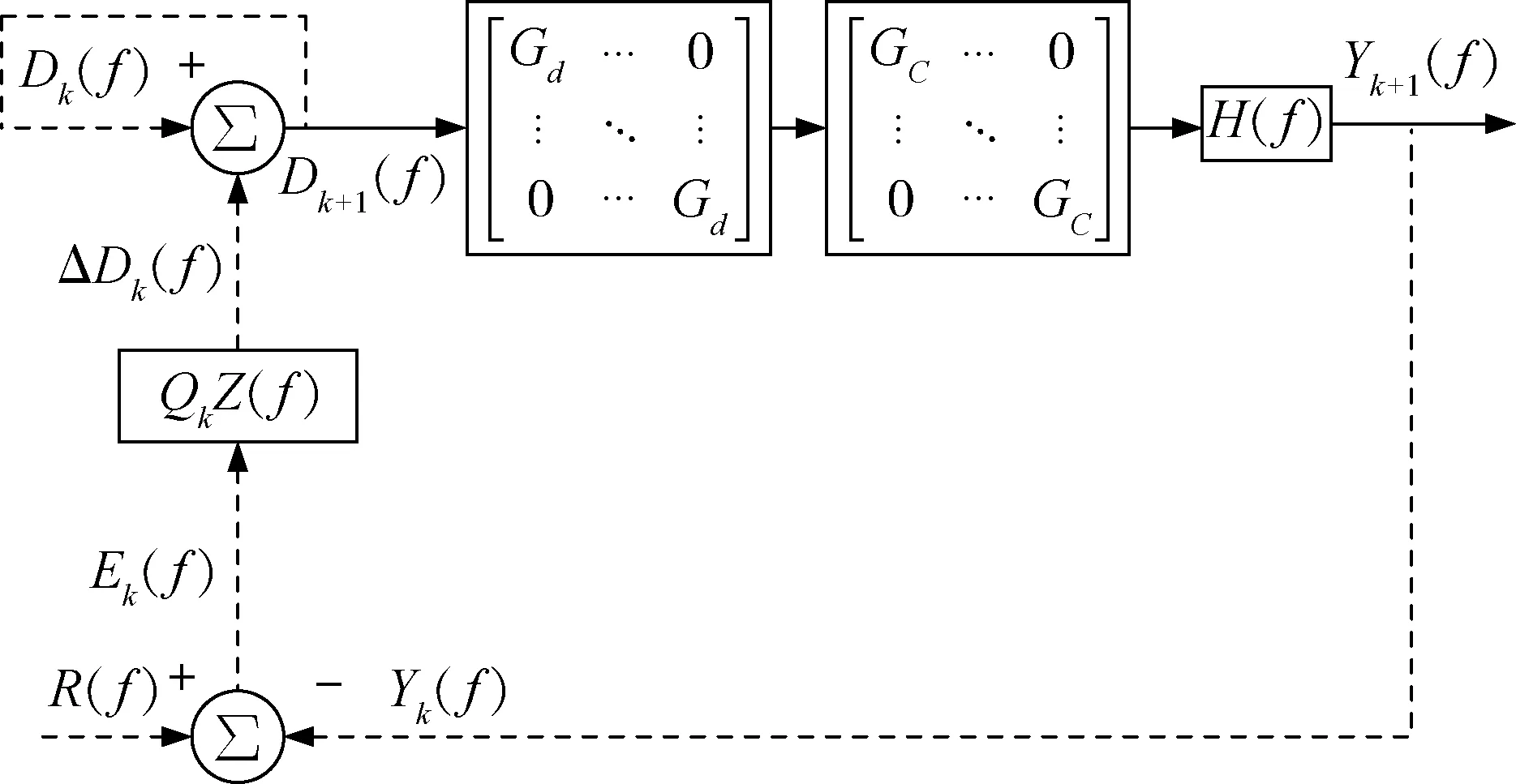
图7 改进离线迭代控制原理图

2.2.1 超前校正设计

被控对象相位滞后过大，影响控制效果，因此需要对被控对象进行超前校正.经典超前校正环节的传递函数[19]具有如下结构:

(8)

超前校正主要用来提供正相位，补偿低频段的激励系统模型误差.最大超前相角为

(9)

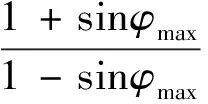
2.2.2 多倍频陷波滤波器设计

陷波滤波器只衰减陷波中心频率处的幅值，对其他频率几乎没有影响.常用陷波滤波器传递函数[19]为

(10)

式中，f0为中心频率，ξ为陷波深度，l为陷波宽度.加速度响应中的多倍频谐波会造成驱动信号包含多倍频成分，确定这3个重要参数的过程为：频域处理初次响应，分析主要谐波，确定n个中心频率；多倍频成分经过陷波器后衰减为原来的ξ，确定陷波深度；目标信号频率范围为5～14.5 Hz，其倍频较接近基频，选取较小的陷波宽度才能保证不会削减基频.

最后，多倍频陷波器传递函数表示为

Gd=

(11)

此多倍频陷波器不会改变基频的幅值和相位，且对多倍频成分具有很好的幅值衰减效果.

2.2.3 收敛性证明

改进离线迭代控制第k+1次误差信号为

Ek+1(f)=R(f)-H(f)W(f)Dk+1(f)

(12)

当目标信号为5～14.5 Hz内的正弦加速度时，超前校正与多倍频陷波器串联，其频响函数表示为

W(f)=ejβ(f)I6

(13)

β(f)为相频特性，表示对原系统补偿的相位.代入式(2)、(4)得到

Ek+1(f)=[I6-αkejβ(f)(I6+ΔH(f))]Ek(f)

(14)

针对已知频率的正弦加速度目标信号，该频率的模型误差简化表示为相位延迟，于是得到

I6-αkejβ(f)(I6+ΔH(f))=

(15)

其中，θij≥β(f)≥0°(i,j=1,2,…,6).

复数坐标系中，αkmiiejβ(f)-jθii与点(1,0)的距离比αkmiie-jθii与点(1,0)的距离小.式(15)对角线各元素满足

|1-αkmiiejβ(f)-jθii|<|1-αkmiie-jθii|

(16)

传统离线迭代控制的收敛条件用F范数表示，则

‖I6-αkejβ(f)(I6+ΔH(f))‖F<

‖I6-αk(I6+ΔH(f))‖F<1

(17)

式(17)表明，当传统离线迭代控制收敛时，即式7成立时，改进离线迭代控制一定收敛.对于相同的控制精度，改进离线迭代控制需要的迭代次数更少，收敛更快.这是因为每一次迭代后，其跟踪误差都小于传统离线迭代控制的.所以，改进离线迭代控制比传统离线迭代控制更具优越性.

3 振动时域波形控制实验

为证明所提方法的有效性，基于Hexapod多自由度微激励系统，开展加速度振动时域波形控制实验.分别采用高频自适应正弦振动控制方法、基于位移反馈的自适应正弦振动控制方法、传统离线迭代控制方法、改进离线迭代控制方法跟踪低频给定正弦加速度.

工况1.目标信号为Z向20 mg的14.5 Hz正弦波，分别采用上述4种控制方法跟踪.两种离线迭代控制方法迭代3次后，所得响应及其时域误差分别与两种自适应控制方法的结果对比，如图8所示.

由图8看出，两种离线迭代控制、高频自适应控制的响应都能很好地拟合目标信号，三者的时域误差都小于20%.在一个波形周期内，不仅改进方法的时域误差基本小于传统方法的，而且改进方法的最大时域误差小于高频自适应控制的，但基于位移反馈的自适应控制方法的最大时域误差却大于30%.

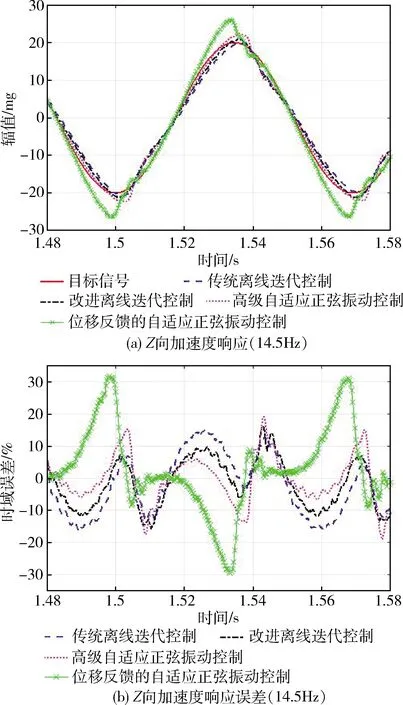
图8 Z向实验结果(14.5 Hz)

第k次实验的相对均方根误差(RRMSE)如下式所示，可用于衡量上述控制方法的控制精度，N表示采集的加速度目标信号和响应信号的长度.

(18)

上述控制方法均采集10 s响应信号，高频自适应控制所得响应的RRMSE为11.23%，基于位移反馈的自适应控制的RRMSE为17.8087%，传统方法迭代3次所得响应的RRMSE为13.71%，改进方法迭代3次所得响应的RRMSE为11.36%.说明改进离线迭代控制和高频自适应控制的控制精度不相上下，且都比传统方法、基于位移反馈的自适应控制的控制精度高.

两种离线迭代控制方法在迭代修正过程中，随着迭代次数增加，响应的RRMSE变化如图9所示，黑色点化线为改进方法，蓝色虚线为传统方法，第0次迭代为第1次实验.由图9可得，每一次迭代，改进方法的RRMSE都比传统方法的小.对于相同的控制精度，改进方法需要的迭代次数更少，这与式17所得结论一致.总而言之，相比传统方法，改进方法不仅加快收敛速度，而且提高控制精度，改善波形跟踪性能.因此，改进方法能保证低频正弦加速度的跟踪精度，从而实现高精度振动时域波形控制.

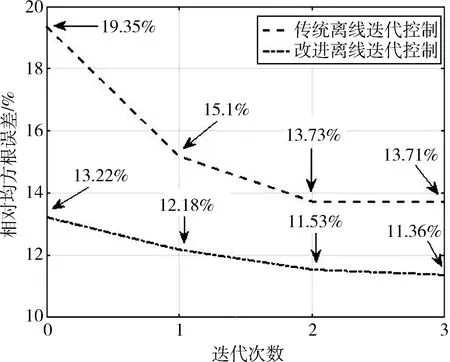
图9 Z向响应信号的相对均方根误差(14.5 Hz)

工况2.高频自适应正弦振动控制方法已无法稳定跟踪10 Hz正弦加速度，故采用基于位移反馈的自适应正弦振动控制方法.不过两种离线迭代控制方法却都能稳定地跟踪Z向20 mg的10 Hz正弦波，前3次实验的响应信号如图10所示.

由图10可看出，迭代修正使得响应信号相对目标信号不断前移，相位滞后角不断减小，说明离线迭代控制可以对延迟系统进行补偿，且具有很好的稳定性.对比两种离线迭代方法的第3次实验结果，可知改进方法明显改善响应波形，说明多倍频陷波滤波器能有效衰减驱动信号中的多倍频成分.分别对比两种离线迭代控制方法的3次实验结果可知，超前校正能有效补偿系统相位，改善离线迭代控制性能，使得改进方法提高波形跟踪精度.

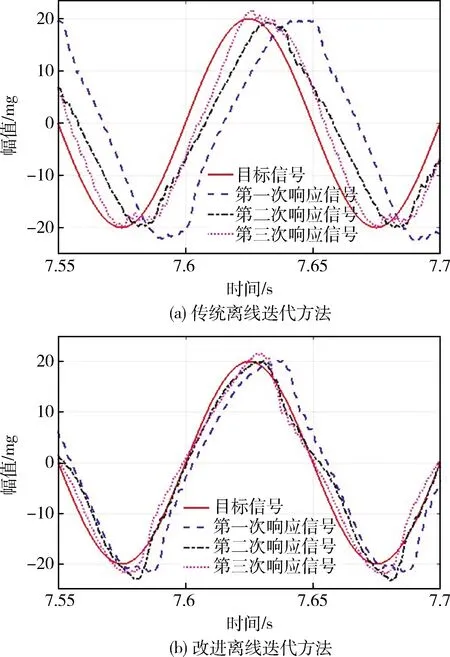
图10 Z向迭代响应(10 Hz)

两种离线迭代控制收敛稳定所得响应，基于位移反馈的自适应控制方法所得Z向加速度响应，对比目标信号及其时域误差如图11所示.由图11可看出，改进方法一个周期内的时域误差基本小于20%，但基于位移反馈的自适应控制方法的最大时域误差高达30%，传统方法的最大时域误差高达35%.而且改进方法的RRMSE为12.66%，基于位移反馈的自适应控制方法的RRMSE为18.02%，传统方法的RRMSE为30.15%.显然改进方法控制精度最高.

工况3.采用改进离线迭代控制、基于位移反馈的自适应控制分别跟踪Z向20 mg的8 Hz正弦波.改进离线迭代控制的最终波形跟踪结果，基于位移反馈的自适应控制所得Z向加速度响应，对比目标信号及其时域误差如图12.由图12可看出，改进方法的响应与目标信号拟合效果很好，一个周期内的时域误差均小于20%，但基于位移反馈的自适应控制的最大时域误差为35%.而且改进方法的RRMSE为17.44%，基于位移反馈的自适应控制的RRMSE为22.18%.可得，改进方法对加速度振动时域波形的控制精度更高.

图11 Z向实验结果(10 Hz)

综上所述，对比自适应正弦振动控制方法，该改进离线迭代控制方法可以将符合精度要求的加速度控制频带下限由14.5 Hz扩宽至8 Hz.

4 结 论

(1)在传统离线迭代控制的基础上，提出一种复合超前校正、多倍频陷波滤波器的改进离线迭代控制，从理论上阐述了其收敛性质，并给出超前校正、多倍频陷波滤波器参数选取过程.

(2)基于Hexapod多自由度微激励系统进行低频给定正弦加速度振动时域波形的控制.由实验结果知，对比传统离线迭代控制，改进方法收敛更快、控制精度更高；对比现有自适应正弦振动控制，其将符合精度要求的加速度控制频带下限由14.5 Hz扩宽至8 Hz.实验结果证明，文中所提方法具有工程应用价值.不过，当目标信号为不同频率的正弦加速度时，响应的主要谐波成分不同，改进离线迭代控制方法中多倍频陷波滤波器的中心频率等参数需重新选取，较繁琐.

图12 Z向实验结果(8 Hz)