让数学走进孩子心里
2020-05-22翁志坚
翁志坚


摘 要:越来越多的教育者认识到,教育要从孩子的最近发展区出发,从孩子身边的事例开始,有效沟通小学数学与生活的联系,让孩子体验数学的严谨与趣味、抽象与直观、枯燥与生动、高雅与通俗,真正让数学走进孩子的心里,与之产生共鸣,才能高效地将数学知识内化为数学文化。
关键词:沟通;联系;体验
建构主义学习理论认为:学习是学习者本身主动的建构活动,学习的内容来自于一定的情境,在真实情境下发生的学习才是最有效的,他可以促使学生从原有的知识和经验正迁移到要学习的知识之中。
在学生的数学学习中,我们要寻找存在于生活中的数学原始问题,再展开探究,进而体现“生活——数学——生活”的知识建构过程。强调数学的“生活味”并非要否定数学的“数学味”,而是要在一个更高的层面上将“数学味”和“生活味”进行有效地融合,最终使“生活味”为“数学味”服务。正如郑毓信教授指出:我们所努力追求的绝对不是由“学校数学”向“日常数学”形式上的简单“回归”,而应该是这两者在更高层次上的自然融合。
一、沟通小学数学与生活的联系,体验数学的严谨与趣味
逻辑性和抽象性是数学学科的本质,在小学阶段特别是低段的学生,正处于由具体形象思维过渡到抽象逻辑思维的一个关键阶段。我们要努力让小学数学课堂洋溢着趣味性,只有让学生对所学的内容产生兴趣,才可以全身心的爱学、乐学、会学、喜学。
小学数学课堂教学有三重境:最低境界是“讲清楚”,其次是“在讲清楚的基础上能讲出趣味”,最高境界是“严谨性与趣味性兼备,定向思维与发散性思维并重”。如果说严谨是一种好品质,那么能够在在严谨中发现趣味,在严谨当中带点趣味就更加完美了。
案例:奇偶性规律
在课堂上,对于这版块的知识,我们还是抡着三板斧:习题演练——发现规律——应用规律,更多的孩子是通过死记硬背来掌握所谓的规律。为此,我利用钉钉群直播和朵朵一家通过连麦《猜数游戏》作了一个大胆的尝试:
首先,我让家长给每个孩子发两张小纸片,让孩子在小纸片上随意写两个数字,不能同时写奇数或者同时写偶数!
接着,要求孩子把右手的数字乘2,左手的数字乘3,然后把左手右手的乘积相加,算好了就把得数默默记在心里不要说出来。
最后,我又叫孩子根据最后算出的得数是奇数的站到家长的左手边,得数是偶数站在家长的右手边。朵朵和甜甜站到了家长的左边,多多和点点站到了家长的右边。“朵朵,甜甜,你们左手都是奇数,多多,点点,你们的左手都是偶数!是不是?”通过连麦,我对着孩子说道。
家长和小伙伴们听的一头雾水,我继续说道“不要着急,实践出真知,我们来亲自算一算,就能明白了,就先依照朵朵的数字重新算一遍吧。”
朵朵左手是1,右手是2,左手乘3即:1×3=3,其实就是奇数×奇数=奇数!
右手乘2的即:2×2=4,其实就是偶数×偶数=偶数!
最后两和相加,就是奇数+偶数=奇数
简单而有趣的一个猜数游戏,就把乘加中涉及的6条规律活生生的展现出来当我说出猜中孩子手中数字奇偶的原因时,小朋友们恍然大悟,原来神奇“魔术”竟然是数学规律啊,原来数学也是这么的有趣啊!
相信,经历过这么有趣而又富有数学味的游戏之后,孩子们对奇偶性的规律一定会有了刻骨铭心的记忆。
课堂,是学生学习知识,提升能力的关键场合,是师生教与学的交融时间,学生的注意力自始至终都要高度聚焦在老师所引导的内容上。我们要在整个课堂进行的时刻,让严谨性在快乐和趣味的氛围中,长时间的萦绕在课堂。
二、沟通小学数学与生活的联系,体验数学的抽象与直观
应用动态数学教学,沟通数学与生活的联系,唤醒或者还原题目的生活味,必将使抽象数学教学的面貌焕然一新。使数学变得更形象、更直观、更易于理解;同时赋予数学趣味性,显得更好玩、更富有吸引力,最终吸引更多的学生喜欢上数学,增强学好数学的信心与决心,达到改变学生“谈数色变”的尴尬局面。艺术是感性的,而数学是思维的体操,是理性的。在整个学习过程中,数学的知识更需要理解与内化,数学的学习方法的优劣直接决定着效率的高低。
A案例:有趣的间隔
在二上《数学广角—搭配》的配套练习里,有这样一道题目对于车票,处于城乡结合部的孩子,认识比较匮乏,更何况需要有“间隔”知识的渗透,为此,在教学本课之前,我特意组织了一次以“认识间隔”为主题的实践活动:
周三下午数学活动课,我组织本班的孩子一起去逛校园,面对着校园小道的一排景观灯,我提出:“大家请看,这条小道上的景观灯,两根灯杆之间的距离是一样的,那假如我们从出口的这根景观灯杆走到下一根景观灯杆的这段距离需要13秒,我们出口的这根景观灯杆为1,国旗前面那根景观灯杆就是3,车库门口边上那根景观灯杆就是7,从我们出口出发到国旗前面和车库门口各需要多少时间?
传来一阵嘈杂的尖叫:“这还不简单,3个13相加和7个13相加喽!”
我又微笑地摇了摇头:“从出口的这根景观灯杆到国旗前面那根景观灯杆一共有几根?从出口的这根景观灯杆到车库门口那根景观灯杆一共有几根?你再想一想。”
“哦,从出口的这根景观灯杆到国旗前面那根景观灯杆一共有3根,第一根到第二根是13秒,第二根到第三根是13秒。我知道了,从出口的这根景观灯杆到国旗前面那根景观灯杆一共要26秒。”
“对,那从出口的这根景观灯杆到车库门口那根景观灯杆一共有几根?要走多少时间?”我接着问。
“要走6段路,”孩子們很快答道,“每段需要13秒,走到车库门口就需要:
13+13+13+13+13+13=78(秒)。”
孩子们真的懂了吗?
“前后有7根景观灯杆,为什么只要走6段路呢?”我又追问了一句。
孩子们异口同声地回答:“因为第一根就是起点,不用再走一段!”
通过这次的实践课,让孩子们收益多多,对“间隔”的认识十分深刻,再一次体验到生活到处藏着数学,相信孩子们如果以后碰到这样的问题,一定会去认真思考和实践!
B案例:《认识时间》
在教学《认识时间》内容之前,我对学生进行了简单的调查,发现大多数孩子对于指针式的手表接触很少,唯一的一点认识,也是在一年级数学课堂上接触的:认识整时。为此,我在教学这个内容之前,先给学生布置了一个课前诊学作业:
画出一天中,你最喜欢的一个时间的钟面,并画出你那时候在干什么!
课堂回放:
(一)复习钟面,整时回顾
结合学生作业:请说出这些同学标的钟面,对不对,没标的,说出是几时?
师:那如果不是整时,分针没有指向12时,生活中我们可以怎么来描述时间呢?
带着这个问题我们一起进入今天的学习——认识时间。
(二)探讨新知,突破知识重难点。
1.感知1时=60分
(1)认时间,看清钟面上的时针和分针很重要。
(2)大格和小格
(3)师:我们让分针动起来,现在是8时1分,继续走是? 8时3分,分钟从12走过了几个小格?8时5分,分针从12到刻度1走过了几小格?(5小格)是多少分?
(4)我们来看看分针走了一圈,走了几小格?是几分?(60小格60分)时针怎样呢?(走了1大格,从8走到了9)时针走了1大格是1时。你知道1时和60分之间有什么关系呢?(板书:60分=1时)一起来说一说。
2.初探认时间的方法
(1)尝试看几时几分
师:结合作业,现在你能看出这几个钟面的时间吗?你是怎么看出来的?
(2)出示学生错误的作品
师:下面我们重点来研究这两个钟面。
师:这些钟面的时针、分针或者时间写的对不对?
3.小结看几时几分的方法
师:看过了这么多钟面,现在请同学来小结一下,怎么来看几时几分呢?
先看时针再看分针。(板书)时针过了几就是几时多,过了8是(8时多),过了9是(9时多)。(板书)分针从12起走了多少个小格,就是多少分。
师:现在你们知道怎样来看钟面了吗?和同桌说一说。抽生说。
从作业中发现,孩子们画的钟面不是很标准,特别半时、整时、满5分之外的时间,但这些并不影响学生对钟面认识的思考。由于面对是身边同学或者是自己的作品,在交流时,很多孩子显出了极大的兴趣,对钟面的特性掌握的非常到位。
这样的诊学作业设计,有效地支撑数学课堂教学,结合社会,联系生活,架设出数学与生活的桥梁,为发展孩子的能力,展开个性学习打开了通道。
总之,需要教师长期有意识地培养、帮助学生理解并掌握数学语言。在课堂上,我们可以根据学生的年龄特点和认知规律,充分提供时空,发挥直观实物的作用,引导学生在对比中尝试用数学的语言去表达;让学生多动手动脑、多说、多画、多想;在操作中学会从数学的角度去思考,在想象中学会用数学的思维去拓展。通过观察、分析、推理、判断、表达等数学活动,完善对数学知识的理解,真正地掌握数学语言。
三、沟通小学数学与生活的联系,体验数学的枯燥与生动
一段时间以来,数学留在多数人心里的感觉是:枯燥的计算+刻板的公式+不能直接应用的远离现实生活的应用题。数学一度被简化为一系列浮在生活之上的一种纯符号的逻辑演绎,数学太抽象、不易理解,导致学生怕学,甚至厌学。面对着形形色色的课程改革,如何才能有效的实施课堂教学?
案例:一万有多大?一千米有多远?
对于这些抽象的大概念、远离学生生活实际并不为人们常用的知识,单凭在课堂上的讲解与分析,显得苍白无力。为了使这些知识变得生动,变得有趣,假期中,我给孩子留了几个作业:
家长传回来的作业,不断地给我以惊喜:
1、雷雅欣和彭怡燃的“感受1千米”的活动
在家长的帮助下,彭怡燃的测量步骤,写得井井有条,相信这次活动中,她一定会对数学的生动有了切身的体会。
2、郑加城和谢博轩的“感受1万大小”的活动
亲身经历过的知识,更容易转化为骨子里的文化,相信1千米的概念,已经在这些孩子的脑海里扎根;1万到底有多大,孩子的潜意识已经有了丰富的表象。
一直以来,教师是在数学的层面上教数学,家长是在生活的层面上辅导数学,我们教师要积极同家长协作,借以丰富的实践活动,向大多数同学认为枯燥无味的数学挑战,使学生在实践活动中感受数学的魅力,爱上数学、乐学数学,从而丰富学生的表象,进而发展学生的数学逻辑思维,优化学生的思维品质。
四、沟通小学数学与生活的联系,体验数学的高雅与通俗
数学是一门具有抽象、概括特点的,研究空间形式和数量关系的独特学科,如何把抽象的、深奥的高雅数学变得鲜活、形象、直观易于学习者接受的通俗数学,变得“好玩”,是每位数学教师的追求。作为教师,我们很有必要在传授知识的同时,要注意搭建数学与生活的桥梁,让学生在实践活动中体验数学给我们的生活带来的惊喜与便捷,以增强学生进一步研究数学的兴趣。
《烙饼问题》案例:数学能让我们的生活变的更美好!
(一)问题导入:在厨房里有一只平底锅,锅一次最多只能放入两块牛排,每块牛排要煎两面,第一面3分钟(包括給牛排“翻身”的时间),第二面由于牛排已经受热,只要2分钟(包括给牛排“翻身”的时间)。煎好3块牛排,至少要多少时间呢?
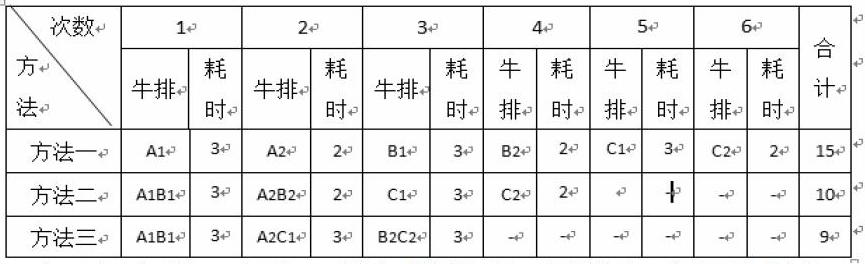
(二)讨论:问题好像很简单!如果一块一块地煎,要15分钟;如果先煎烤2块,再煎第3块,3块牛排只要10分钟就可以煎好
(三)质疑:我们可以发现第三、四次锅里只有一块牛排,还可以放一块牛排,还可以好好利用起来!假如把三块牛排的煎烤顺序调整一下会更省时间
由于第二次放入了第三块生牛排,考虑到如果在2分钟时先取出第一块牛排,再给第三块牛排煎烤1分钟,那樣会多耗时半分钟,干脆就连续煎烤3分钟好了;第三次放入的虽然都是反面,由于第一块牛排取出来冷却了,所以也需要3分钟才可以熟。这样三次,锅里一直都有两块牛排,算了一下,9分钟,还是能节省一分钟!理想是这样的:
(四)实践:事实又是怎样的呢?同学们难以抑制内心的喜悦,回家马上把自己的发现付诸于行动!
(五)再讨论:第二天,程铱同学反馈她的困惑:第一次3分钟煎烤,顺利结束!在准备第二次煎烤时出了点小意外:给牛排翻个身还是方便的,关键是把那个半生的牛排取出来装盘子里候着,就显得有点麻烦!终于等到了第三次煎烤,她费了好大的劲才把那个盘子里半生的牛排再装到锅里进行第三次煎烤!结束时,她看了一下时间:11分钟!
面对着这尴尬的结果,她十分不解地问我:“为什么我做到了让锅里面始终有两块牛排,明明是9分钟,怎么结果却适得其反,时间用得更多呢?”我笑着说:“你看一下你的操作视频,你煎烤的时间确实是节省了1分钟,但是把半生的牛排拿出来和放回去的时候,却比平时多花了2分钟!”原来现实是这样的:
(六)新问题:我轻轻地说:“考虑问题的时候,不能只从一个角度(煎烤牛排的时间)思考,要结合其他相关因素进行分析,合理的方法用在合适的地方,才是好方法!”
……
数学方法千变万化,生搬硬套地使用,往往会适得其反!只有根据实际情况,选择合理的方法,才能实现策略的最优化!或许,这是孩子们这次煎牛排最好的收获!
没有哪一门课程能像数学这样让人绞尽脑汁又不讨好。哈代告诉我们:学好数学多少得有点兴趣,还得动点脑筋,否则苦不堪言,谁还有心情欣赏它的美呢?
不过,当你真正喜欢上数学,迷上数学,走进数学的话,那就好了,你的生活就是数学的生活,你的数学就是生活中的数学!
参考文献
[1] 王乐.爱的浇灌,使孩子健康成长.《新课程.小学》2018年第08期
[2] 朱伟 于嘉.知识传授·精神培育·人格塑造的三位一体——文化人类学视域下的大学生人格培养. 《成才之路》2008年22期
[3] 周正英. 关注每一个孩子的成长——小学班主任工作浅谈. 《好家长》2017年46期
