某长大缓倾顺层边坡支护效果的离心实验研究

郭永春， 冷景岩， 施金江， 杨军杰

(1.西南交通大学 地球科学与环境工程学院， 四川 成都 610031；2.中国铁路设计集团有限公司， 天津 300251；3.中铁四院集团 南宁勘察设计院有限公司， 广西 南宁 530003)

长大缓倾顺层边坡是指边坡坡长大于100 m[1]，岩层倾角在15°～20°甚至更低缓的顺层边坡[2]，由于岩层倾角较小，坡高相对不高，一般情况下该类边坡处于稳定状态，但在降雨、施工、地震等扰动的情况下会出现失稳。根据笔者的调查，在西南红层地区分布有大量的长大缓倾顺层边坡，近年来普遍出现了由于各种诱发因素导致的滑动现象，已经成为西南红层地区的区域性边坡问题，长大缓倾顺层边坡问题应引起重视。

国内外对缓倾顺层边坡的支护治理已有不少的研究成果，赵建军等[3]认为缓倾顺层边坡中下部是影响稳定性的关键块体，对关键块体进行强支护可以达到保证边坡安全的效果；陈静曦等[4]对某缓倾边坡进行了滑坡推力计算，提出了削坡减荷的治理方案；王文亚[5]提出了对缓倾顺层岩质边坡采用对拉锚索挡墙支护形式，并采用“双控法”确保施工精度；毛明等[6]对某缓倾边坡进行预应力锚杆加固处理，并通过数值模拟验证了方法的可行性。这些治理措施大都只是针对于坡长较短的缓倾边坡，对于坡长更长，推力更大的长大缓倾顺层边坡并不适用，而双排抗滑桩是加固大型滑坡的常用工程技术[7-9]，但在长大缓倾顺层边坡治理方面的理论研究还十分有限。

不同于自重应力下的静力模型实验，离心模型实验能够通过离心加速度的变化，使实验模型达到与原型相同的应力水平，较好地模拟原型应力状态下坡体的变形特征[10]。近年来，离心模型实验在常规边坡分析中的应用日益广泛，但在长大缓倾顺层边坡中鲜有研究。

某铁路长大缓倾顺层边坡在路堑开挖时出现了滑动破坏现象，为保证铁路路基安全，拟采用双排桩进行支护治理。为深入研究双排桩对该长大缓倾顺层边坡的控制效果，在地质调查和稳定性分析的基础上，拟采用离心模型实验进行深入研究，为工程安全提供参考。

1 离心实验设计

1.1 地质背景

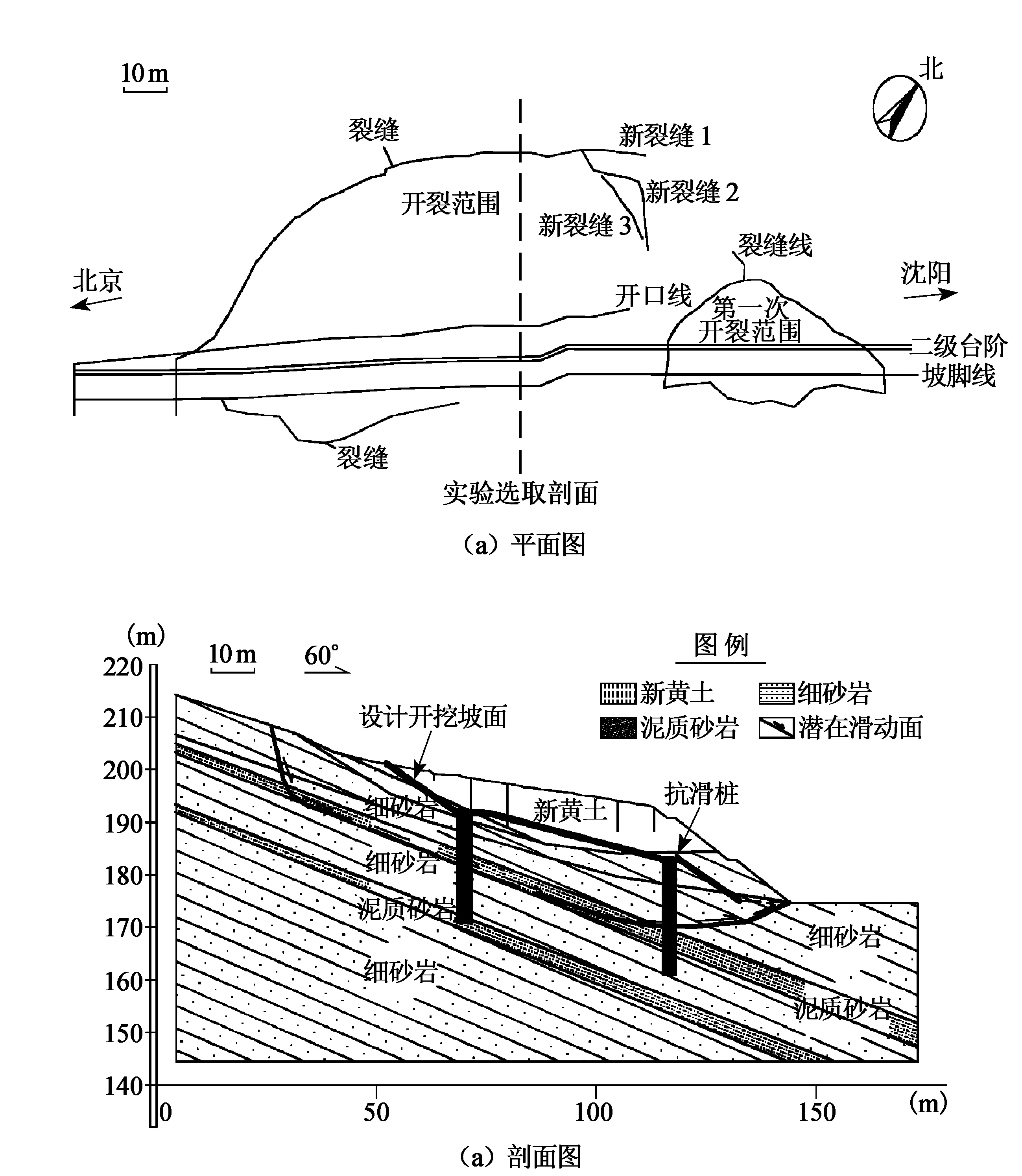
图1 边坡地质剖面

边坡位于某客运专线路基段，该段地层上部覆盖新黄土，下伏侏罗系中统土城子组细砂岩、泥质砂岩，节理裂隙发育，岩体破碎。由于工程需要，开挖边坡坡脚，加上连续强降雨，泥岩夹层软化，边坡发生滑动破坏，采用的治理方案是削坡减荷和双排矩形抗滑桩对其进行加固，边坡地质平面图和剖面图如图1所示。

1.2 离心实验方案

根据研究目的，首先是模拟没有进行支护时，边坡开挖失稳机理，以下简称为“无支护边坡模型”。然后在无支护边坡模型的基础上，增加双排抗滑桩，研究边坡支护控制效果，以下简称为“双排桩支护边坡模型”。两个实验方案相互衔接，模拟实际的工程施工过程。

1.3 模型相似参数

实验采用西南交通大学离心实验室TLJ-2土工离心机，离心机的主要技术指标见表1。

表1 离心机主要技术指标

受模型箱的规格和容重限制，确定几何相似比n模∶n实=1∶180，模型几何参数如表2所示。

表2 滑坡模型与原型尺寸

为实现等应力模拟，模型与原型不但要满足几何相似，还要在各个对应点的应力、应变满足相似关系，故取应力相似比为1。

边坡滑床基岩原型为岩性较好的细砂岩，模型选用200号水泥砂浆模拟，具有足够的强度和刚度，防止其在实验中发生变形，保证滑体沿着既定的滑带下滑。边坡滑体原型为风化破碎的细砂岩，模型材料选用与原型密度、弹性模量相似的细砂岩，实际边坡中，砂岩为中厚层砂岩，根据几何相似比，需要切割成厚度为3 mm的薄片。滑带原型为泥质砂岩，模型材料根据粘聚力和内摩擦角相似关系，选用不同的相似材料[12]进行配比，确定配比方案为粘土∶水∶黄油∶细砂=6∶1∶1.9∶1.35，该模型土的粘聚力c=2 kPa，内摩擦角φ=14.25°，可作为滑带的相似材料。

模型桩主要承担桩后岩体推力，发生弯曲变形，故模型桩的抗弯刚度作为选取相似材料的主要考虑因素。根据抗弯刚度相似原理，实验采用铝合金材料，其厚度为1 mm，根据几何比尺制成相应的尺寸，模型桩参数见表3。

表3 抗滑桩实验原型和模型尺寸

1.4 模型制作与实验过程

1.4.1 无支护边坡模型

根据相似比确定的模型尺寸，在模型箱体内壁绘制滑坡的形状；在底部和侧壁铺设一层塑料薄膜，保护模型箱在实验过程中不被刮损破坏；固定好外侧挡板，将调制好的200号水泥砂浆逐步倒入模型箱内，填筑滑床，磨平，夯实，直到设计标高，等待水泥砂浆凝结，在凝结过程中要注意喷水养护。按照确定的配比方案制作滑带土材料，按照原状土的密度将等重量的材料铺设在滑面上，分层铺设，层之间刮毛，确保滑带土材料贴合，完整。按照绘制的形状，将切割好的砂岩薄片堆砌成滑体。在滑体前沿铺设一层塑料薄膜和报纸，倒入水泥砂浆，制作反压水泥块。实验中通过移走反压块的方式模拟现场开挖。实验采用WYDC-10L型位移计，模型制作完毕后，将位移计布置在相应位置，监测坡体位移，如图2所示。

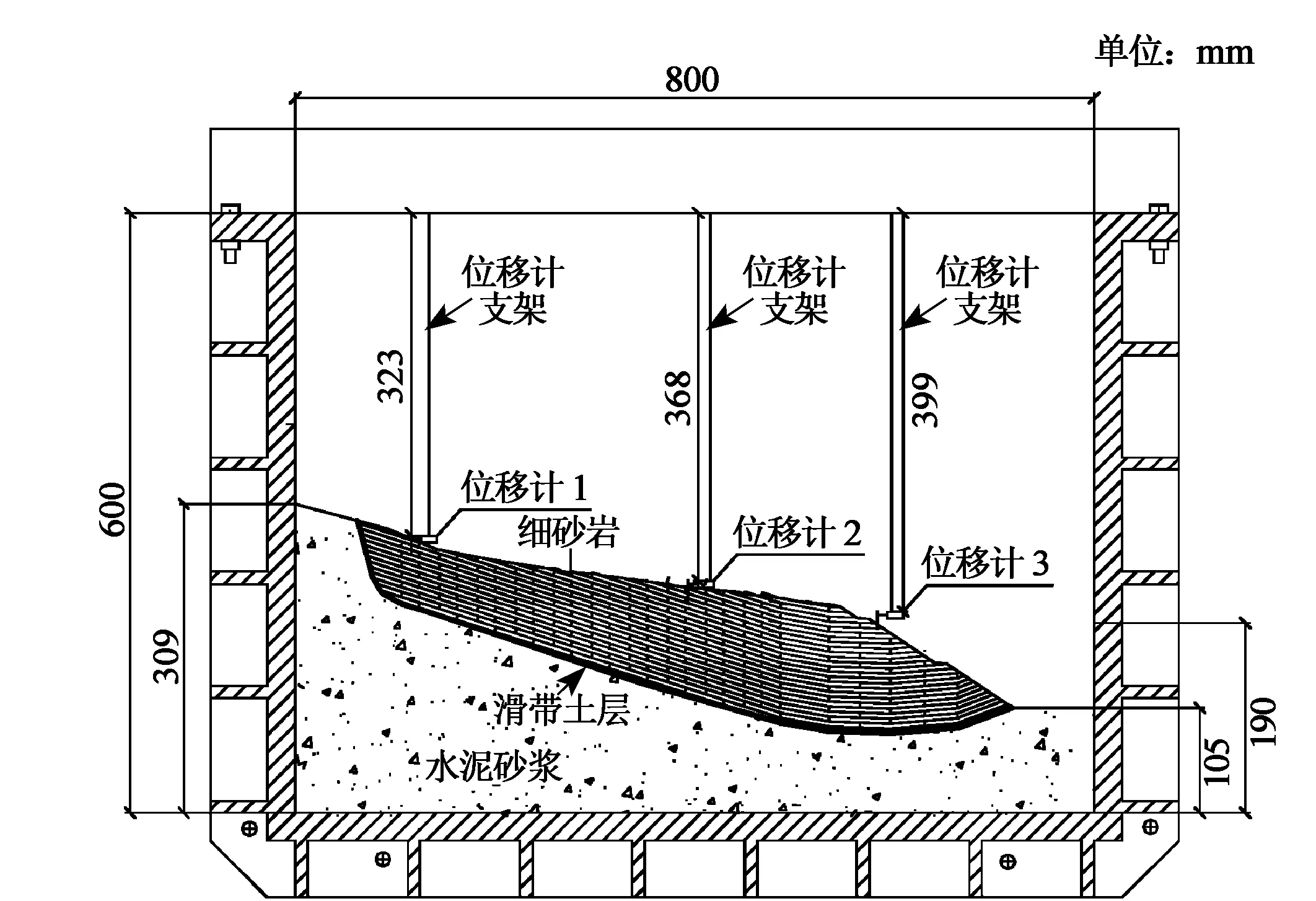
图2 无支护边坡模型示意图

1.4.2 双排桩支护模型

无支护边坡模型实验结束后，在滑床的对应位置，切割凹槽，布置模型桩，并用与滑床配比一致的水泥砂浆填补缝隙，等待至固结，其余步骤同无支护边坡模型，如图3所示。由于尺寸限制，在模型桩管内侧布置了3对应变片，分别粘贴在模型桩的上、中、下3处，确保应变测试分别位于滑动面的上下两侧。应变片主要粘贴在铝合金管内壁两侧，导线从上端引出。在埋入滑床内部时，注意应变片用硅胶保护，防潮。

在边坡模型侧壁绘制2 cm×2 cm的网格(图4)，并在坡面设置4条水泥条带(图5)，条带上设置刻度，用以监测坡面裂隙。无支护边坡模型与双排桩支护模型采用相同的实验加载过程，步骤如下：(1)离心机提供30g离心加速度预压，预压时间为30 min；(2)待测试原件数据稳定，移去反压水泥块，离心机提供165g离心加速度，稳定后维持60 min；(3)关闭离心机，将离心速度降至0。

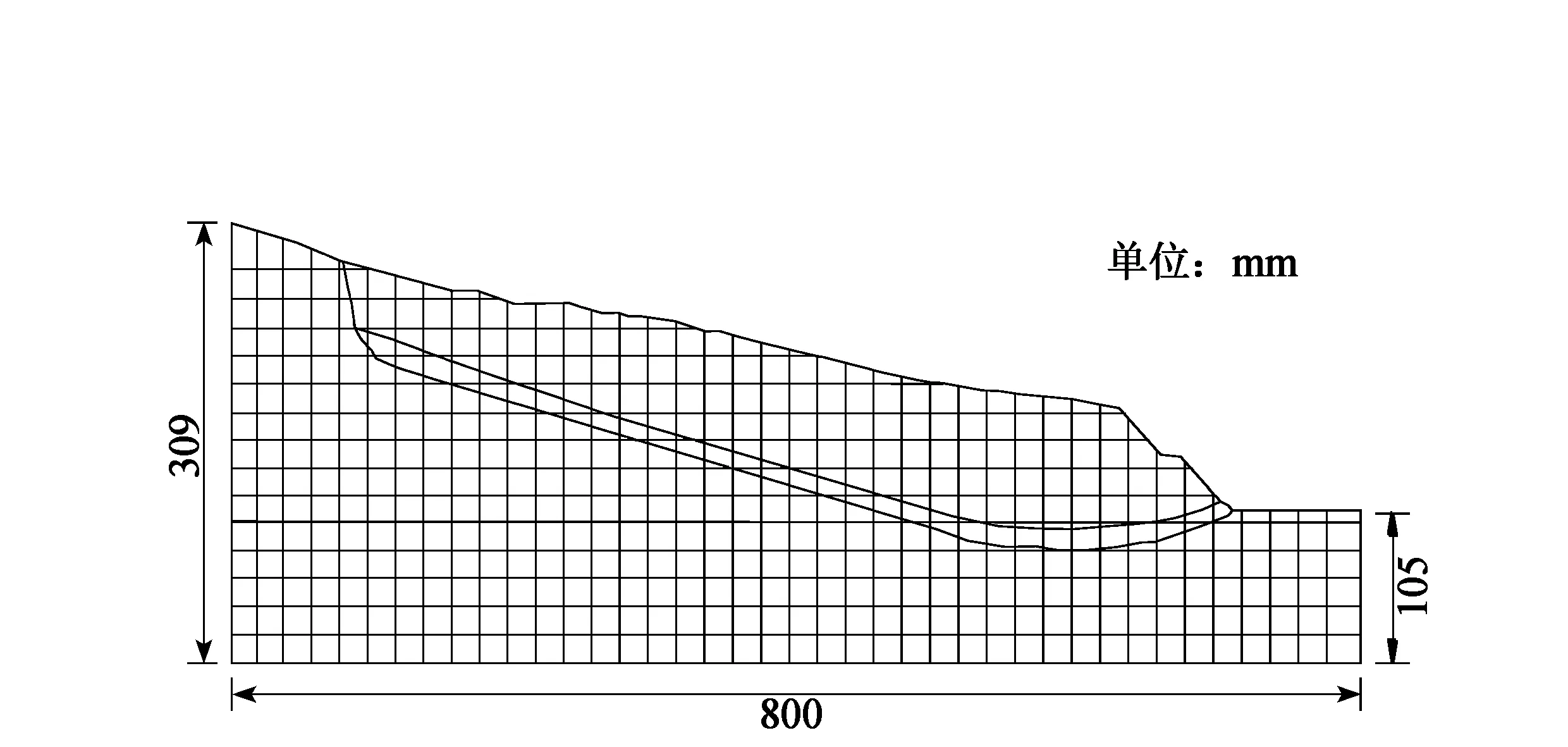
图4 边坡模型侧壁网格

图5 坡面裂隙监测条带

2 离心实验主要成果

2.1 坡面位移

2.1.1 无支护边坡模型

无支护边坡坡面位移随时间变化曲线如图6所示，为了对比，采用数值模拟软件模拟了离心实验模型对应监测点的数值模拟结果(如图6中的理论曲线所示)。图6结果表明，无支护边坡坡面位移随着加载时间和离心加速度的增大而增大，并随着离心加速度阶梯式的加载方式而出现阶梯式的形状。离心加速度在30g匀速转动时，坡面位移最大为0.24 mm；当离心加速度增加到165g时，位移为1.33 mm；当模型在离心加速度165g稳定运转7 min后，坡面位移达到最大，为3.9 mm。根据相似比，实际中位移为0.70 m。

2.1.2 双排桩支护模型

双排桩支护边坡坡面位移曲线如图7所示。当离心加速度达到设计值165g时，坡面位移稳定在0.04 mm，按照几何比例尺计算，对应实际坡面位移为7.2 mm。

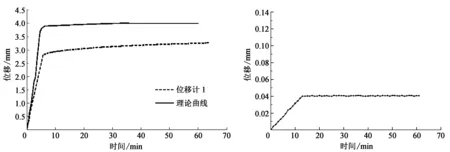
图6 无支护边坡坡面位移曲线 图7 双排桩支护边坡坡面位移曲线

2.2 桩身弯矩

2.2.1 桩身弯矩随深度变化趋势

根据桩身变形数据，计算桩身弯矩变化曲线如图8所示。桩顶、滑带附近、桩底部实验计算弯矩分别为77.5、11 080.8、142.284 kN·m；后排桩桩顶、滑带附近、桩底部实验计算弯矩分别为184.27、26 443.33、52.13 kN·m。利用理正软件计算得到抗滑桩弯矩图(图9)，对比离心实验弯矩分布趋势与理论弯矩分布趋势，说明了实验测试结果的合理性。实验结果说明设置的抗滑桩充分发挥了控制边坡变形的作用，保证了边坡的整体稳定性。

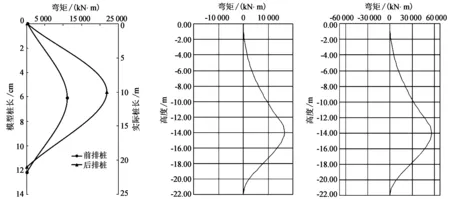
图8 测试断面的平均弯矩随桩深的变化 (a) 前排桩 (b) 后排桩 图9 理正软件计算桩身弯矩图

2.2.2 桩身弯矩随时间的变化

根据应变片数据，计算得到对应位置的桩身应力。根据公式对滑面处后排桩进行分析，绘制了该截面后排桩的弯矩-时间关系曲线(图10)。可以看出，后排桩滑面处桩身应力随着离心加速度的增大而增大，并在165g时达到最大值0.003 8 kN·m。根据弯矩相似计算，对应的弯矩为22 161.6 kN·m，而计算值为26 443.336 kN·m，实验值与对应截面的弯矩计算值对应较好。

从前排桩滑面处桩身弯矩-时间关系曲线(图11)可以看出，在离心加速度加载到165g时，应力最大达到0.001 9 kN·m，并且保持稳定。通过相似比换算，对应的弯矩为11 080.8 kN·m，而理论计算值为13 099.224 kN·m，实验值与对应截面的弯矩计算值符合程度较好。

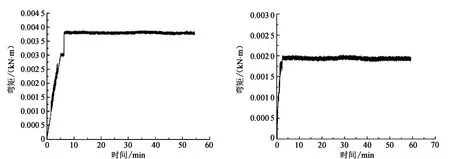
图10 后排桩身弯矩随时间变化曲线 图11 前排桩身弯矩随时间变化曲线

前排和后排抗滑桩桩身弯矩变化趋势表明，在持续边坡荷载的作用下，抗滑桩有效发挥了抑制边坡变形的作用，保证了边坡的稳定性。

2.3 坡面裂隙和侧面网格变形

2.3.1 无支护边坡模型

2.3.1.1 边坡坡面裂隙分布

实验前水泥条带完整，无裂隙，实验后4条水泥条带后部都有两条明显的裂隙，裂隙主要产生在坡体的后部和前部。在坡体后部，有两条贯通整个模型横向的裂隙，缝隙宽约为0.5 mm。裂隙统计如表4所示，说明边坡坡体产生了整体滑移变形。

表4 观测条带上裂隙分布情况

2.3.1.2 边坡侧面网格变形

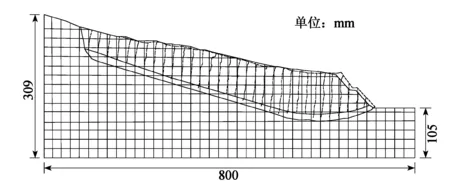
图12 无支护边坡侧壁网格变化

在实验过程中，在模型的剖面方向绘制了均匀的2 cm×2 cm观测网格，观测坡体整体变形规律。对比实验前后模型侧面的网格对应位置的变化，绘制出前后坡体不同位置的位移变化如图12所示，图中实线表示实验前网格线，虚线表示实验后网格线。从图中可以看出，开挖后，边坡侧面网格变形最大处约为12 mm，说明无支护边坡坡体产生了较为显著的变形破坏，降雨入渗和边坡开挖诱发了边坡活动。

2.3.2 双排桩支护模型

2.3.2.1 双排桩支护后边坡坡面裂隙分布

离心模型实验时，在坡面设置了4条水泥条带，监测坡体表面在失稳变形过程中，裂隙发生和发展规律。实验后观察，双排桩支护边坡坡面只有4条裂隙，是坡面出现的局部裂缝。

2.3.2.2 边坡支护后剖面变形

观测结果表明，双排桩支护模型剖面网格线几乎没有变形，说明在削坡卸荷和双排抗滑桩治理后，能有效控制边坡变形，该边坡处于稳定状态，说明双排桩治理边坡是有效的。

3 结果分析与讨论

3.1 对长大缓倾顺层边坡问题的讨论

对于长大缓倾顺层边坡，在一般概念中，边坡是基本稳定的，尤其是边坡坡度低于20°，甚至是15°以下的缓倾顺层边坡。然而，无支护边坡模型和双排桩支护边坡模型的离心实验结果表明，长大缓倾顺层边坡在适当的条件下，如降雨、工程开挖等因素诱发下，是可能产生活动的。实验研究结果与已有研究结论是一致的。

3.2 双排桩支护效果评价

离心实验结果表明，双排桩支护前，边坡坡面最大位移达到3.25 mm，设置双排抗滑桩支护后，边坡坡面位移最大为0.04 mm，有抗滑桩支护后的坡面位移减小了3.21 mm，即支护后坡面最大位移量降低了约98%，说明双排桩支护措施有效地控制了边坡的变形。

通过边坡坡面变形、桩身变形、坡体位移、桩身弯矩等实验数据的对比分析，充分说明该边坡的下滑力作用到了桩身上。且抗滑桩承受土体荷载后，桩土相互作用维持了边坡的稳定，双排桩对边坡变形起到了较好的控制作用。

3.3 离心实验方法在长大缓倾顺层边坡研究中的应用评价

通过两组长大缓倾顺层边坡离心模型实验，较好地模拟了长大缓倾顺层边坡开挖失稳、支护治理整个施工过程，有效获取了边坡坡体变形、位移、弯矩等坡面裂隙信息，尤其是边坡坡体剖面变形信息、桩身变形信息。这些信息与地质勘察、理论分析阶段的资料相互验证，互相补充，丰富了对边坡进行分析研究的基础数据，为深化长大缓倾顺层边坡的研究提供了有效的方法。

4 主要结论与建议

通过离心模型实验，模拟了对长大缓倾顺层边坡开挖支护过程，重点进行了无支护边坡模型和双排桩支护模型的实验研究，主要得出以下结论和建议：

(1)通过精心设计，离心实验方法可以获得较为丰富的实验数据，是研究长大缓倾顺层边坡问题的有效方法；

(2)长大缓倾顺层边坡在开挖、降雨等诱发因素作用下是可能发生活动的，在工程建设中应引起重视；

(3)双排桩支护措施有效控制了边坡变形，该措施是适用于长大缓倾顺层边坡的。