有关隐圆及一线三等角题型解题
2020-05-22
中学的学习在同学们的学习生涯中是非常重要的阶段,这个阶段的数学学习尤为重要,为了提高同学们的数学学习效率,本文就有关隐圆及一线三等角题型展开探讨,希望能为同学们的学习提供一定的帮助。
一、隐圆
几何最值问题是中学数学的难点之一,而隐圆问题是常见的一类题型,此类题目常常出现在填空最后一题或压轴最后一问,是作为难点拉开分值的问题。同学们在学习时要重视这一问题,要掌握这个模型的重点知识。

图1

图2
如图1 所示,圆外一点P连接圆心与圆交于A,B两点,则P到圆上最近与最远的距离分别为PB和PA。如图2 所示,CH垂直于AB时,CH为圆上点到AB的最大距离。米勒最大张角问题:如图3 所示,点A,B为OM边的两个定点,点C是ON边上的动点,当C在切点处时,∠ACB最大。
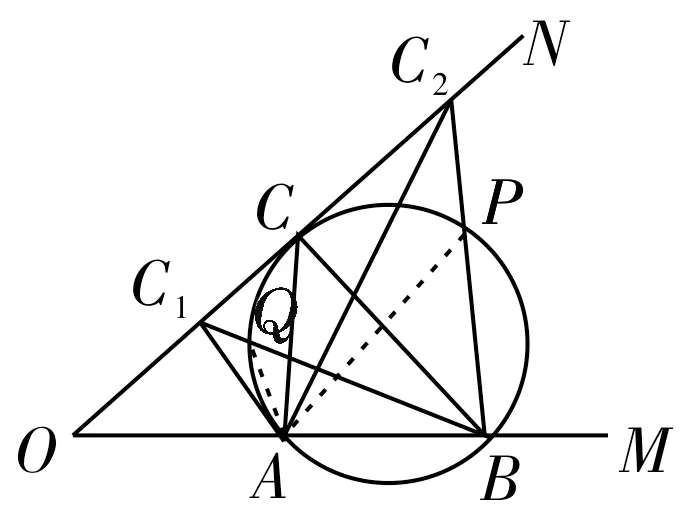
图3
(一)定点定长
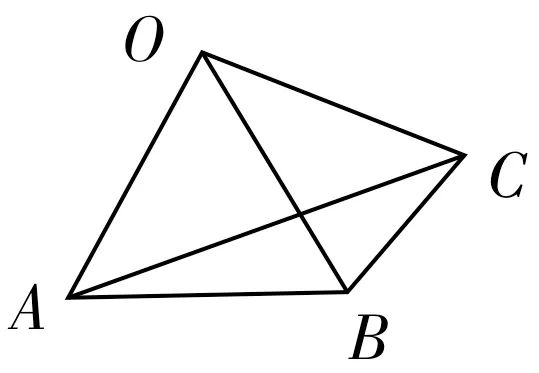
图4
例1如图4 所示,在四边形OABC中,AB=OA=OB=OC,则∠ACB=____度。
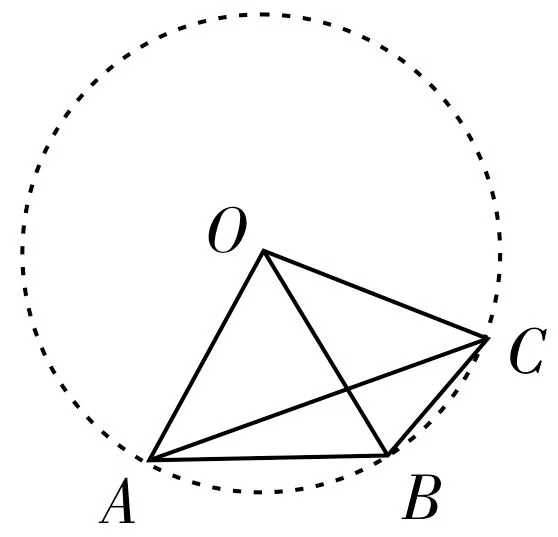
图5
分析:由题意可知A,B,C三点到O点的长度相等,由此想到“定点定长存隐圆”。那么A,B,C三点就在以O为圆心、OA为半径的圆上(如图5所示),此时问题就很容易解决了。
(二)定弦定角
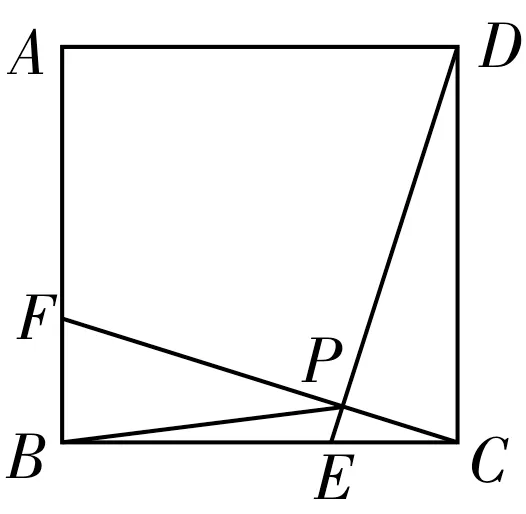
图6
例2如图6 所示,在正方形ABCD中,点E,F是AB与BC上的两个动点,CE=BF,连接DE与CF相较于点P。连接BP,则BP的最小值是_____。
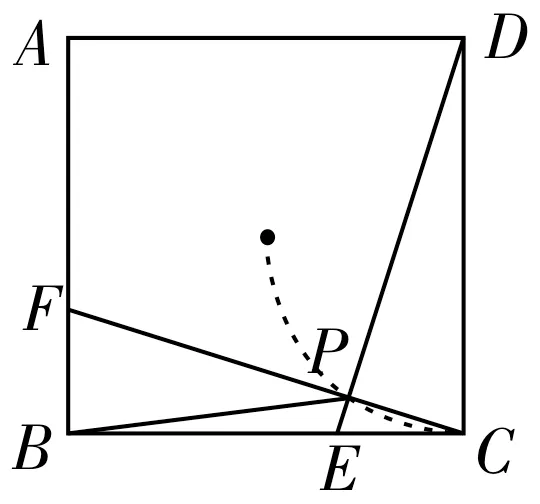
图7
分析:根据题意不难判断△ECD≌△FBC,可得CF垂直于DE。我们发现不论E、F两点如何运动,∠CPD始终是直角,并且∠CPD所对的边CD固定(如图7所示)。
二、一线三等角
1.一线三等角的类型。

图8
(1)同侧型,如图8所示。
(2)穿越型,如图9所示。
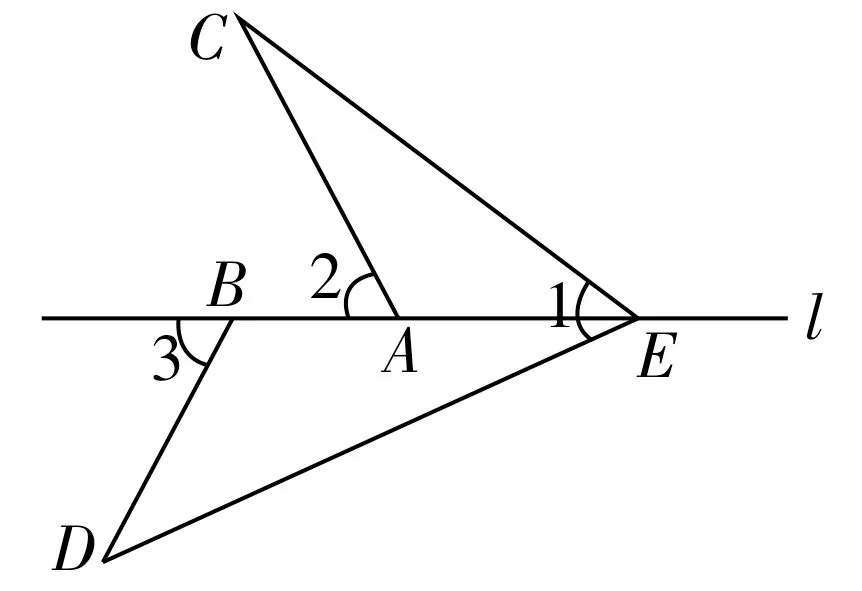
图9
2.一线三等角的应用。
(1)主要有三种状态:一是只有一线三等角的情况;二是先给出一线二等角,不用一等角;三是直线上只有一个角。
(2)建立一线三等角的步骤,首先是找角,其次是找线也就是定线,最后便是构相似,如图10所示。

图10

图11
例3如图11所示,在等腰直角三角形ABC中,∠BAC=90°,D为AB上一点,连接CD,P为CD上一点,∠BPD=45°,若CP=6,△ACD的面积为18,则线段DB的长为____。
分析:解答此题需要先从点A作AE⊥CD,然后在CE上取一点F,使∠AFE=45°(图略),所以△AFC∽△CPB,由此得出在等腰Rt△AEF中,AE=3,根据S△ACD=18,可以推出CD=12,那么△BDP∽△CDB,得出BD2=PD·CD,最终求得
