基于ARIMA-BP组合模型的房地产价格预测方法研究

尤豫心　陈继红

摘要：针对使用单一预测模型存在数据特征提取不充分，预测精度不高的问题，提出了一种基于ARIMA-BP组合模型的房地产价格预测方法。结合ARIMA模型处理线性问题的优势以及BP神经网络模型在非线性问题上的优势，利用误差方差加权平均训练法训练出最佳权重的组合并建立组合模型对某市区房地产价格和趋势预测进行实证分析。理论分析和实验结果表明，所提两者的组合模型有效解决了不能充分提取数据特征，预测精度不理想的问题，比单一预测模型能获得更准确的预测效果。

关键词：房地产价格;ARIMA模型;BP神经网络模型;组合模型;趋势预测

中图分类号：TP391文献标识码：A

文章编号：1009-3044（2020）09-0264-06

1 引言

当今时代，房地产业是我国国民经济的支柱型产业，它在国民经济中具有高度的产业关联度，是推动整个国家国民经济发展、加速实现工业化和城市化的主导力量。房地产业持续健康有序的发展在国家经济的运作、政治的建筑、人民生活水平的改善中占据举足轻重的地位。然而，由于影响房地产发展的因素多种多样，例如，社会状况、人口密度、房地产价格政策、税收政策、城市发展规划、宏观经济状况、物价状况、居民收入状况、自然因素和区域因素等都对房地产的发展有着不同程度的影响，致使房地产市场发展不成熟，部分城市存在严重的区域差异问题，严重影响我国经济的突飞猛进以及进入世界强国的步伐。因此，基于数据挖掘技术探索出一套实用的预测方案研究房地产价格的变化趋势迫在眉睫。面对海量的房地产数据，如何分析挖掘出有价值的数据，如何通过大量数据揭示一种新的关系、趋势和模式成为一个研究热点。

文献[1]结合AR模型良好的模型辨识能力和神经网络良好的非线性映射能力以及遗传算法的全局最优能力，改进算法并建立IGA-NARLMBP预测模型用来预测都江堰上游来水。

文献[2]利用时间序列分析方法，以时间序列的平均值、标准差、ACF系数、PACF系数及AIC值、BIC值等参数与模型的评价准则，建立陕西省GDP时间序列模型，预测未来6年的经济发展。

文献[3]基于具有代表性的ARIMA模型与BP神经网络模型建立了针对某餐饮020企业的组合模型，并分别对整体、商家、城市三种企业不同的预测场景进行了模型的实现与验证。

除此之外，文献[4]采用时间序列AR模型进行震动趋势预测，通过ARIMA模型的平稳化处理，将非平稳的序列平稳化，模型参数估计使用了参数估计无偏、精度高的最小二乘法，验证结果表明AR模型能夠很好地拟合振动信号时间序列，达到了理想的预测精度。文献[5]提出了组合预测的思想，将参与组合的各种预测结果通过合适的方法进行组合，取其精华，弃其糟粕，获取最优预测结果。

目前，组合预测理论已经证明：多种预测模型的组合在一定的条件下能更有效地改善模型的拟合能力和提高预测精度[6]。将统计方法的代表ARIMA模型与人工智能方法BP神经网络有机结合，充分发挥二者的优势，建立房地产价格预测模型，研究房价的变化趋势并对房价进行预测，有助于房地产行业有序发展。

2 房地产价格预测模型

2.1 ARIMA模型

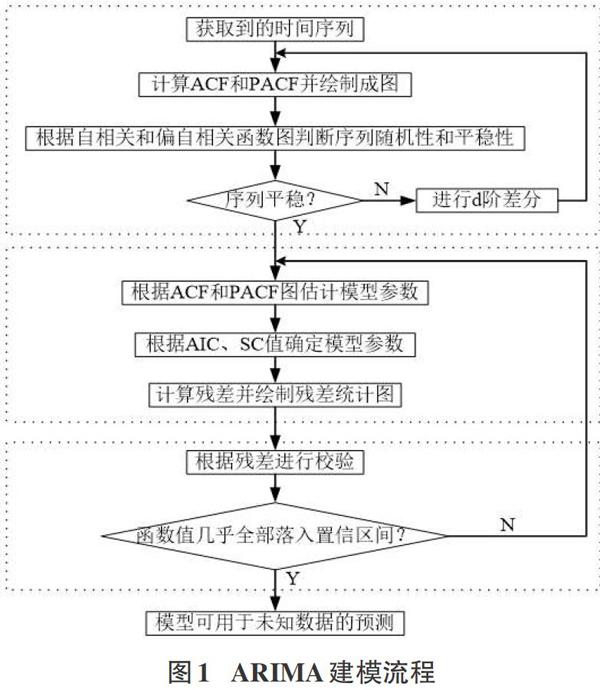
时间序列模型是一种重要的现代统计分析方法，广泛应用于自然领域、社会领域和科学研究等。作为一种重要的时间序列模型，差分自回归移动平均模型（ Autoregressive IntegratedMoving Average Model，ARIMA），得到了广泛的应用[7，8]。它是由Box等[9]提出的一种时间序列建模方法，主要由三部分组成，分别为AR（P）自回归模型、MA（q）模型、ARMA（p，q）模型，模型建模步骤简单，其变量主要借助内生而不依赖于其他外生变量，但在建模前必须要求序列具备平稳性与随机性特征。基于ARI-MA模型的房地产价格趋势预测方法的建模主要涉及四个步骤：数据的平稳化处理，序列平稳化，模型的识别与定阶，模型的校验，具体流程如图1所示。

在模型的识别与定阶阶段，重点在于根据自相关与偏自相关函数的拖尾、截尾情况来确定具体需建立哪种模型最为合适，具体的模型识别规则参照表1。

2.2 BP神经网络模型

大数据时代，人工智能方法在预测、关系拟合、分类等领域已广泛应用。对于非线性系统，神经网络具有通过学习逼近任意非线性映射的能力，将神经网络应用于非线性系统的辨识和预测，可以不受非线性模型的限制。

自1982年Hopfield发表了关于自反馈神经网络的文章[10]以及Rumelhart等人发表了专著PDP[11]以来，研究神经网络的热潮便在世界范围内掀起。随后，BP神经网络在1986年由Ru-melhart和McCelland为首的科学小组提出，是一种按照误差逆向传播算法训练的多层前馈网络，由1个输入层、若干隐含层和1个输出层构成[12]。同层的神经元之间并无关联，异层的神经元之间则前向连接。BP神经网络拓扑结构如图2所示。

在整个BP中，重要的是两个环节，第一环节是信号实现从输入层到输出层的前向传播，另一部分是在输出层未得到期望输出时，误差信号则会继续沿着原来的网络连接路线返回并通过不断修改各层之间的权值以得到最终的期望误差。目前，BP神经网络在函数逼近、系统辨识与预测、分类以及数据压缩等方面均发挥着不可替代的作用，成为人工智能领域的热门[13]。

BP神经网络作为人工智能领域的代表，具有较强的非线性映射能力，能够以任意精度逼近任何非线性连续函数;良好的自学习和自适应能力，便于将学习内容记忆到网络的权值中去;良好的泛化能力与容错能力，有益于将学习成果应用于新知识。当然，BP算法也有其固有的缺点[l4]，算法容易陷入局部极值导致网络训练失败、算法存在预测能力与训练能力矛盾问题，有时训练达到某种极限后，训练能力虽然提高了，预测能力反而会下降，导致过拟合现象。一般情况下，BP神经网络建模过程为：

（1）网络初始化，即给输入变量，各连接权值等分别赋予一个数据归一化变换，将数据映射为[-1，1]内的随机数，并设定好相关参数，误差函数、精度值以及最大的学习次数等[15]。随后，取样本序列作为输入，并选出合适的激活函数，一般Sigmoid函数较为常用，公式为：

（2）信号利用激活函数沿着网络正向传递，分别得到隐含层和输出层的输出以及损失函数的期望值，损失函数计算公式为：

其中0表示参数集合，y表示真实值，y表示预测值，1/n表示总误差的平均值。

（3）若输出结果未达到期望误差，则误差信号在网络中反向传播，并根据误差不断更新网络中的权值和偏置项。

（4）重复以上2-3步，直到最大学习次数用完或者损失函数小于事先给定的阈值，此时网络中的各参数即为模型最佳参数，则模型训练结束，可用于实时预测。

2.3 组合模型

各个单项预测模型的方法和原理各不相同，不同预测模型挖掘信息的角度也不同，它们之间的关系不是相互冲突的，而是相互关联，互相补充的[16]。在实际预测中，如果因为某项模型预测误差偏大而丢弃，则会导致该项模型所能挖掘出的有用信息缺失，造成更大的误差。多项研究证明，将多个单项预测模型选择性结合形成组合模型，更能有效降低预测误差，提高模型精度，进而提出组合模型的概念。

组合模型是提高模型预测精度的最佳方法之一，可依据特定的方法对各种子模型预测精度效果进行权衡、分配权重，基于预测精度高的模型权重大，预测精度小的模型权重小的原则，选取合适的权重判定方法对组合模型进行验证对最终的预测效果至关重要。常用的组合模型判定方法有以下三种：

1）等权平均法：即将各子模型的权重平均化，各子模型权重相等，权重总和为1。公式为：

通过组合模型的创建，综合多种单项预测模型的结果，可为数据的预测和分析提供更精准的预测方法，得到更为系统、全面的预测效果。

3 模型应用

作为江苏长江经济带的重要组成部分，南通集“黄金海岸”和“黄金水道”优势于一体，具有巨大的发展潜力。本文选取南通市某区2013年01月至2017年12月，共计60个月的数据用于建立模型，2018年01月至02月的数据为校验数据，验证模型的精确度。以此为例，阐述预测过程。

3.1 ARIMA模型建立

1）数据清洗

借助SQL Sever平台提取2013-2017年房地产每月销售均价，对其进行数据清洗工作，剔除保障性限价房、安置房、车库等特殊房源數据，利用SPSS工具对一些离群点进行数据转换，使其在一定程度上接近正常值，尽可能减少对预测结果的影响。

2）序列平稳化处理

对于时间序列的平稳性处理与判定，本文案例基于两种数据分析工具，采用两种方法进行判定。初步采用SPSS 23.0工具绘制时间序列的自相关与偏自相关函数图进行判定，若序列平稳，则不做处理，若不平稳，则通过差分平稳化，本文案例通过一阶差分后的自相关与偏自相关函数如图3所示：

由上图可知当K>3时，自相关函数图都落人置信区间，且逐渐趋向于0，证明序列具备平稳性和随机性，验证了差分次数的正确性。

为了再次验证其准确性，基于Eviewsl0.0工具，对上述差分次数后的时间序列进行单位根校验，校验结果如图4所示：

由一阶差分后的单位根校验结果图可知，在1%，5%和10%的显著性水平下，检验统计量均小于相应的DW临界值，从而拒绝H0，再次验证序列的平稳性与随机性，可用于模型的识别与定阶。

3）模型识别与定阶

ARIMA模型的建立涉及参数的估计与阶数的确定，可基于计算时间序列yt的自相关与偏自相关函数，即观察上述图3，并根据模型识别规则来确定，借助Eviewsl0.0工具所计算出模型参数估计如图5所示：

4）模型校验

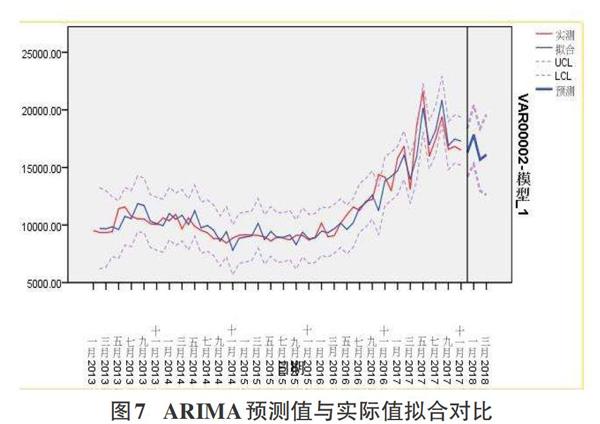
传统的模型检验为DW统计量检验，使用该检验方法需满足三个条件：一阶自相关、回归中有截距项、回归因子无滞后项[7]。而本文案例采用观察残差自相关函数图的结果以及最终ARIMA模型拟合图进行校验，校验结果如图6、7所示。

由上图可知，残差序列几乎全部落人置信区间，验证了数据序列为白噪声，即通过检验。月均价实际值与模型预测值达到了很好地拟合，再次验证模型通过校验。

3.2 BP神经网络模型建立

1）数据预处理

BP神经网络收集到的数据与网络模型算法要求的数据具备一致性，在建模之前，需对数据进行归一化处理，借助MAT-LAB的Mapminmax函数实现，函数负责将矩阵的每一行数据压缩到[-1，l]。基于数据挖掘技术可得到月均价时间序列x0， X1， X2，…，Xk， Xk+l， Xk+2，"，Xk+i，将XO， X1，X2，…，Xk作为训练样本用于建立模型，Xk+1，Xk+2，…，Xk+1作为测试样本用于验证模型的准确性。房价数据具备波动性，每个月不断地更新变化，选取距离当下日期越近的数据用于建模，模型对未来预测准确性的影响力度越大。本文案例中，为了充分利用数据，不断使新数据覆盖旧数据，选取每相邻三个月的数据预测下一个月的数据，如对2018年01月的数据进行预测，则选取2017年10月、11月、12月的数据用于训练。

2）网络参数设计

（1）输入层与输出层节点设置

本文案例中，选取的策略是以近邻三个月的数据预测下一个月的数据，即可确定输入层节点数为3，输出层节点数为1。

（2）隐含层节点的设置

隐含层节点数的选择直接影响神经网络模型的各项性能指标。根据众多研究学者的研究经验可得公式来确定具体的节点数：h=√m+n+a，其中，h代表隐含层的节点数，m、n代表输入层与输出层节点个数，a为1-10之间的调节常数，具体的h值可以通过实验进行试探性的确定。

（3）训练函数的确定

BP中的训练函数直接影响BP算法的预测结果，负责调解权值和阈值，以使整体误差最小化。具体选取的训练函数可以根据数据的特征以及经验试探性来确定。

（4）学习速率的确定

在BP神经网络中，学习速率的选择直接影响算法迭代效率。本文案例选取的学习速率为0.01。

（5）期望误差值

BP中的期望誤差值可以根据每次训练的结果对比来确定。通过多次实验研究对比，本文案例的期望误差值选取为0.001。

在数据预处理与建模思路确定以后，便可基于MATLAB环境搭建BP神经网络结构预测模型，建立的BP神经网络训练图及均方误差图如图8、9所示。

依据图8、9可知，本案例采取Levenberg- Marquardt算法，算法训练迭代次数达到113次时，均方误差已达到期望误差，训练结束，最终BP训练出的月均价拟合如图10所示。

由拟合图可以看出，网络输出房价与实际房价达到了较好的拟合效果。通过研究分析，自2013年01月至2017年12月，不同月份之间的月均价上下波动，但总体的房地产价格走势呈现上升趋势，由前期48个月的缓慢上升，到后期12个月的迅速上升趋势，可总结出2017年的房价较其他几年数据呈现极端性，这可能是因为国家经济宏观调控、城市规划变动或其他因素所致，对于房地产的趋势预测来说，是一个值得额外关注的重点，更值得引起相关部门的关注。

综合图7和图10中ARIMA和BP神经网络拟合结果可以看出，ARIMA模型很好的提取了数据的线性特征，模型预测出的房价趋势与实际房价具备一致性，但对于个别区间的极值，未能准确拟合。而通过BP神经网络的多次训练，除了预测趋势一致外，实际值与预测值达到了高于ARIMA模型的拟合效果，几乎全部拟合。

3.3 组合模型建立及校验

通过实例分析可知，ARIMA模型能够更好地提取出房地产数据之间的线性特征部分，而BP神经网络模型则最大限度地发挥了数据之间的非线性优势，因此，根据组合模型的相关理论，将二者结合建立组合模型效果更为有效。为了保持数据集的一致性，选取南通市近60个月的房价数据进行建模。基于组合模型现有的权重判定理论，通过多次实验对比分析，本文案例在原有误差方差加权平均法的基础上进行改进，采用误差方差加权平均训练法对模型进行权重判定，建立ARIMA-BP并联组合模型，对房价进行预测分析。建模具体思想为将ARI-MA模型和BP神经网络模型的训练拟合值作为组合模型的输入向量，依据ARIMA模型与BP神经网络模型的预测结果计算误差方差，再对其进行排序，随后基于单一模型权重与误差方差成反比原理赋予权重，并通过多次训练对比，不断调整权重参数，训练组合模型，以实现ARIMA-BP并联组合模型的建立。组合模型为：

f（x）=w1 V1（X）+w2V2（X）

（12）

其中，wi为第i种模型的权重，V1 （X）、V2 （X）分别为ARI-MA模型和BP神经网络模型在x时间下的预测值。实验结果显示，ARIMA模型的误差方差较大，预测精度相对较小，而BP神经网络模型的误差方差较小，预测精度较大，且本文案例仅涉及两种单项预测模型，故按照误差方差加权平均法原则以及多次的实验训练对比分析，借助Lingo软件平台，利用两种单项预测模型的房价拟合值，最终计算得到组合模型的权重分别为0.33和0.67。

依据模型各项评价指标理论基础，本文案例中用来验证模型精度的指标如下：

平均绝对百分比误差（MAPE）：

其中，yi表示真实值，yi表示预测值，n为单一模型的个数。

基于以上三种方法得到的各单项模型与组合模型拟合及预测对比结果如表2和表3所示：

从实验结果可以看出，基于误差方差加权平均训练法的组合模型具有较高的预测精度，在训练数据集一致的情况下，ARIMA模型的评价指标较大，平均绝对百分比误差为10%，BP神经网络模型次之，且精度明显得以提高，而两者的组合模型指标又有了进一步的改善，为8.0%，显示组合模型效果最佳。 本文在研究了近60个月份房地产价格的变化趋势下，为了再次验证组合模型的实用性，对2006年-2020年南通市崇川区商品住宅的销售价格进行了预测分析，选取2006年-2018年的数据为训练集，2019、2020年的数据为测试集，预测结果如图11所示。

由图11实验结果可知，随着年份的更新迭代，崇川区的房价整体呈现增长趋势，自2006至2011年增长趋势较为平稳，在2011年呈现局部极大值，随后四年有缓慢下降趋势，过程较为平缓，但在2017年和2018年出现急剧增长，波动较大，这与国家政策的宏观调控以及人们日常的刚需紧密相关。基于对三种模型的比较分析，可以明显看出三种模型的预测系列线与崇川区年均价系列线基本拟合，其中，组合模型几乎完全拟合，达到了最为理想的效果，验证了组合模型的实用性与优越性。

4 结束语

利用各种单项模型建立组合模型实现对房地产价格的预测研究是一种有效的方法，具有较高的理论与实践价值。本文介绍的基于误差方差加权平均训练法的ARIMA-BP并联组合模型实现了对房地产价格的精确预测效果，模型可靠，易于实现，具有一定的应用价值。

本文建立的模型也存在一些不足，以下几个方面有待进一步的改进：

（1） BP神经网络易使算法陷入局部极值，致使最终训练失败。本文所论述的组合模型对BP神经网络模型分配了较大的权重，可能会因此带来弊端，影响预测效果，是需要进一步改善的地方。

（2）房地产价格的影响因素众多，本文所做的各项研究均是基于时间序列预测方法进行的，未将影响房价变化的各种因素考虑在内，可能会使预测的结果较为片面，这需要进一步的扩展研究。

（3）数据集的数量多，参考的依据范围大，对于模型预测的结果说服力度更强，本文所选取的数据集在数量上有所欠缺，这也需要在后期的研究中做出改进。

目前，组合模型的研究遍布于统计学、计算机学、大数据领域。综合多个单项预测模型优缺点建立组合模型的研究方向已得到一定的进展。随着研究的深入，組合模型将具备更好的可用性与优越性，应用的领域空间必将得到进一步拓展。

参考文献：

[1]罗凤曼.时间序列预测模型及其算法研究[D].成都：四川大学，2006.

[2]魏宁.时间序列分析方法研究及其在陕西省GDP预测中的应用[D].杨凌：西北农林科技大学，2010.

[3]施佳.基于ARIMA-BP组合模型的某餐饮0：0企业订单预测研究[D].北京：北京交通大学，2018.

[4]徐峰，王志芳，王宝圣.AR模型应用于振动信号趋势预测的研究[J].清华大学学报（自然科学版），1999，39（4）.

[5] Bates J M，Granger C W J.The combination of forecasts[J].Jour-nal of the Operational Research Society， 1969，20（4）：451-468.

[6]秦大建，李志蜀.基于神经网络的时间序列组合预测模型研究及应用[J].计算机应用，2006，26（S1）：129-131.

[7] Zhang G.Time series forecasting using a hybrid ARIMA and neural network modeI[J].Neurocomputing， 2003，50：159-175.

[8] Contreras J，Espinola R，Nogales F J，et al-ARIMA models topredict next-day electricity prices[Jl. IEEE Transactions onPower Systems， 2003，18（3）：1014-1020.

[9] BOX G E P，JENKINS G M.Time Series Analysis， Forecast-ing and ControI[Ml. San Francisco： Holden day， 1970.

[10] Hopfield J J.Neural networks andphysical systems with emer-gent collective computational abilities.[Jl. PROCEEDINGS OFTHE NATIONAL ACADEMY OF SCIENCES OF THE UNIT-ED STATES OF AMERICA，1982，79：2554-2558.

[11] Rumelhart D E，McClelland J L，.Parallel distributed process-ing[M].The MIT Press， 1986.

[12]陈基纯，王枫.房地产价格时间序列预测的BP神经网络方 法[J].统计与决策，2008（14）：42-43. [13]李萍，曾令可，税安泽，等，基于MATLAB的BP神经网络预测系统的设计[J].计算机应用与软件，2008，25 （4）：149-150，184.

[14]杨晓帆，陈廷槐.人工神经网络固有的优点和缺点[J].计算机科学，1994，21（2）：23-26.

[15]樊振宇.BP神经网络模型与学习算法[J].软件导刊，2011，10（7）：66-68.

[16]闫海霞.灰色组合预测方法在粮食产量中的应用[D].西安：西安理工大学，2009.

[17] Berkhin P.A Survey of Clustering Data Mining Techniques[J]. Grouping Multidimensional Data， 2006， 43（1）：25-71.

【通联编辑：梁书】

基金项目：国家自然科学基金自助项目（61872263）

作者简介：尤豫心（1996-），女，河南南阳人，硕士研究生，研究方向为数据挖掘;陈继红（1966-），男，江苏南通人，硕士研究生，副教授，研究方向为数据挖掘。