缺失值条件下基于LSTM单特征输入的短波频率预测研究

尚教凯　贺寅　徐池　徐铭

摘要：研究中发现，将短波远程通信中两点间的可用频率作为单特征输入，利用长短期记忆人工神经网络（ISTM）可以实现对未来几天短波频率进行预测。该文对输入的样本数据存在缺失值条件下的情况进行分析，最终得到缺失值条件下该方法的应用策略，对远程短波通信保障具有重要意义。

关键词：频率预测;LSTM;缺失值

中图分类号：TP319 文献标识码：A

文章编号：1009-3044（2020）09-0251-04

1 引言

短波通信一直是海上远程通信不可缺少的手段。科学技术的不断进步推动着短波通信向着建链速度更迅捷、数据传输容量更大的方向发展，但实现准确的短波通信频率预测是制约着远程短波通信质量提升的关键问题。

现有的ITS-HF系列短波频率预测软件虽然能够实现复杂链路程序化，但该系列预测软件的输入条件过于苛刻，且局限性较强，在实际海上通信过程中的效果并不好。而短波频率作为典型的非线性时间序列，有很多学者基于模糊小波、神经网络、混沌理論等算法对时间序列预测开展研究，任淑婷采用模糊小波神经网络方法对短波频率进行预测，预测值与实际值的相对误差在9%左右，但工程实现难度较大。

根据深度学习擅长提取非线性时间序列数据特征的特点，通过时间半年，间隔一小时的频率样本数据对长短期记忆人工神经网络（ ISTM）进行训练，实现了对未来约20天每小时为间隔的点对点短波远程通信频率预测。在实际应用过程中，收集样本数据过程中存在出现数据缺失的可能，这种情况就不能满足预测模型对样本数据中时间间隔为一小时的训练需求，那么出现这种缺失值时，该模型是否还能实现频率预测？缺失比例是否对预测结果产生影响？

为进一步明确基于LSTM实现频率预测方法对样本数据的需求，本文对样本数据存在缺失值的情况进行分析。

2 LSTM模型

3 缺失值处理

数据收集过程中出现缺失值存在以下几个原因，一是没有历史经历，未积累过相关资源;二是有历史经历，资源积累过程中因为设备原因出现缺少丢失，比如数据未存储成功、设备故障导致某些数据未收集或者未传递到数据库中;三是出现奇异样本，不适合被调用，处理过程中被删除。

缺失值的处理办法包括填充和删除，而填充的方法包括：

1）当调用的数据集中出现缺失值时，将所有缺失值用NULL进行填充，表示该项空值，不影响使用，

2）平均值填充。用该属性其他值的平均值对该缺失项进行填充。

3）用最可能的值填充。本系统中频率生成子模块能够根据一定数量的样本进行频率预测，当可通频率存在缺失时，该预测值就是最可能的值，用预测值进行填充能够补充缺失项。

为更好地明确缺失值对基于LSTM单特征输入实现频率预测的影响，本文对样本数据中缺失值的处理办法是删除该项的整组数据。

4 仿真模型构建

1）仿真环境

本文的仿真是在Python3.7环境下采用Python语言实现的，为满足Python中numpy库（Numerical Python，Python进行科学计算和大数据分析的基础库）导人数据要求，需要将仿真数据存储为.csv或.xlsx格式文件。

2）仿真数据

由于数据需求量多，难以获得能够满足算法训练要求的实际数据，本文提取“亚大预测”模型预测结果中的两点间最高可用频率（Maximum Usable Frequency，MUF）替代短波可通频率作为模型验证的仿真数据。

数据由两部分组成，一部分是由2014年8月31日0900至2015年3月1日0800的跨度半年，间隔1小时的时间，另一部分是北京市石景山区与福建省福州市台江区两点间通信的最高可用频率的数值。以上两部分组成了4368组该时刻最高可用频率的样本数据集合，如下表所示：

通过Python编程，在数据预处理过程中，对仿真数据进行缺失值处理，包括连续缺失、随机缺失两种方法，进行缺失值处理后继续进行下一步。

3）为能够验证该模型的训练效果，需要测试样本与预测结果进行比对，因此，在仿真实现过程需要将预处理后的仿真数据划分成训练样本集和测试样本集两部分。

4）确定能够评估短波频率预测效果的评价指标。这里选用均方根误差（ RMSE）作为计算短波频率预测值与测试值误差的公式。

5）将整个仿真的结果可视化，便于观察进行对比分析。这里使用Python中的matplotlib库进行实现。

整个仿真实现流程如图1所示：

5 仿真结果与分析

缺失值的情况分为连续缺失以及随机缺失两种，下面通过Python软件对这两种情况进行仿真，根据仿真结果进行总结分析。

5.1 连续缺失情况

在基于LSTM单特征输入实现频率预测的方法中，当需要调用的样本数据集从中间部分连续缺失比例为12.5%时，运行结果如图2所示。其中图2（a）中的蓝色部分为训练区域，黄色部分为预测区域，横轴代表日期，坐标间隔为1个月，纵轴代表频率值，单位为MHz。图2/b）中黄色线条为预测值，蓝色线条为实际值.横轴为日期，坐标间隔为6小时，纵轴为频率值，单位为MHz。

当需要调用的样本数据集从中间部分连续缺失比例为25%时，其预测值结果如图3所示：

5.2 随机缺失情况

当需要调用的样本数据集中随机缺失比例为1.25%时，其预测值结果如图4所示：

当需要调用的样本数据集中随机缺失比例为2.5%时，其预测值结果如图5所示：

当需要调用的样本数据集中随机缺失比例为15%时，其仿真结果如图6所示：

当需要调用的样本数据集中随机缺失比例为20%时，其仿真结果如图7所示：

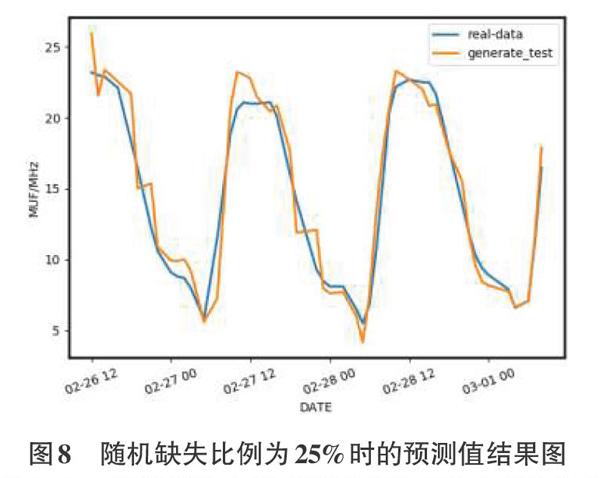
当需要调用的样本数据集中随机缺失比例为25%时，其仿真结果如图8所示：

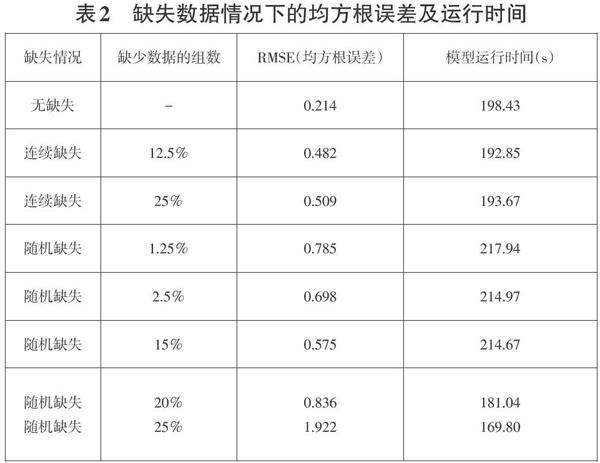
基于LSTM单特征输入实现频率预测方法在缺失数据情况下的均方根误差及运行时间如表2所示：

通过对以上图表对比分析，可以总结如下：

（l）从2（a）中可以看出两块蓝色部分中间的白色区域为样本数据集中缺失部分，通过图表观察可以发现在单特征输入频率预测模型中连续出现缺失值与未出现缺失值时相比RMSE值偏大，模型运行时间稍少一些，但拟合效果较好，仍能够满足预测精度需求。

（2）随机缺失数据情况下RMSE值比未出現缺失值时大，随着随机缺失数据增多，模型运行时间减少。

（3）当随机缺失比例达到20%开始，预测精度难以满足通信需求，因此当可通频率资源库中可提供的样本数据集中随机缺失比例达到20%以上时，单特征输入频率预测模型的预测结果不可靠。

6 结语

本文通过对样本数据中的缺失值情况进行分析，总结得出当训练样本数量不少于3000组，时间间隔1小时，随机缺失比例不高于20%的条件时，基于LSTM单特征输入模型能够用于实现短波频率预测。

参考文献：

[1]贺骁，刘芸江，肖瑶，等.基于传播损耗的短波自适应快速建链[J].电讯技术，2014，54（3）：302-306.

[2]杨青彬，余毅敏，余奇，等.基于lTS软件的短波频率管理系统设计[J].电讯技术，2013，53（3）：249-253.

[3]田晓铭，张海勇，徐池，等.泛Kriging法在海上短波通信频率预测中的应用[J].电讯技术，2018，58（12）：1434-1440.

[4]黄少昆，王伟民，黄子洋，等，电离层F2层临界频率预测方法探讨[J].气象水文装备，2009，4（20）：19-21.

[5]简相超，郑君里，混沌和神经网络相结合预测短波通信频率参数[J].清华大学学报f自然科学版），2001，41（1）：16-19.

[6] Wang Y C.Short-term wind power forecasting by genetic algo-rithm of wavelet neural network[C]//2014 International Confer-ence on Information Science，Electronics and Electrical Engi-neering， April 26-28， 2014. Sapporo， Japan. IEEE， 2014：1752-1755，

[7]任淑婷，郭黎利.基于模糊小波神经网络的短波频率预测[J].通信技术，201 1，44（4）：37-39.

[8]徐池，邱楚楚，李梁，等.海上短波通信频率优选技术现状与分析[J].通信技术，2015，48（10）：1101-1105.

[9]尚教凯，张海勇，徐池，等.基于LSTM单特征输入的短波可用预测研究[J].舰船电子工程，2019，39（11）：76-78，88.

[10]邓建新，单路宝，贺德强，等.缺失数据的处理方法及其发展趋势[J].统计与决策，2019（23）：28-34.

【通联编辑：朱宝贵】