基于高压压汞和核磁共振的致密砂岩渗透率预测
2020-05-21王付勇周树勋
程 辉,王付勇,宰 芸,周树勋
(1.中国石油大学(北京)非常规油气科学技术研究院,北京 102249;2.中国石油长庆油田分公司油田开发事业部,西安 710021)
0 引言
致密油等非常规油气资源是目前国内外勘探开发的热点[1-2]。美国自2008 年Bakken 致密油藏成功规模开发以来,已发现Williston 和West Gulf 等多个致密油气藏盆地,建成主力产区4 个[3]。2018 年,致密油产量占到了美国石油总产量的59%,约650 万桶/d(1 桶≈0.158 9 m3),表现出巨大的勘探开发潜力[4-5]。我国致密油气资源主要分布在鄂尔多斯、准噶尔和松辽等盆地,相关勘探开发研究表明,我国致密油资源总量丰富,但对其相关研究起步较晚,虽然近年来在鄂尔多斯盆地新安边地区等多个区域已经取得工业油流,但在致密油的有效开发方面仍面临许多挑战[1,6-8]。
致密储层的孔隙度一般小于10%,基质覆压渗透率小于0.1 mD,孔喉直径小于1 μm,原油以吸附或游离状态赋存于储层中,具有低孔、低渗的特点,孔喉尺寸从纳米级到微米级不等,孔喉结构复杂,连通性差[1,9]。油藏物性的好坏往往决定了储层中流体流动的难易程度[10],而渗透率是评价储层物性的重要参数之一,准确预测致密砂岩渗透率对致密油气藏开发具有重要意义。研究致密砂岩孔隙结构及渗透率的方法主要有高压压汞、恒速压汞、核磁共振、CT 扫描、X 射线衍射及扫描电镜等[11-13]。利用高压压汞和核磁共振等测试虽然可以直接得到岩心的孔隙度、渗透率等参数,但实验往往成本较高,耗时耗力[14]。渗透率预测模型是指利用油藏的孔喉半径、孔隙度等物性参数来预测储层渗透率的数学模型,所预测的渗透率多为平面渗透率,不同的模型对不同区块和层位具有不同的预测精度,具有简单、快捷和成本低廉等优点[15]。渗透率预测模型可以分为两大类,一类是基于压汞测试获得的岩心物性参数进行渗透率预测的模型,这类模型较多,如Winland 模型、Swanson 模型等[16-17];另一类是基于核磁共振测试T2频谱数据预测渗透率的模型,这类模型多是基于SDR 模型和Coates 模型改进而来,如SDR-REV 模型[18]。致密油藏的渗透率与其他物性参数之间的关系随层位不同具有明显差异,选择合适的渗透率预测模型不仅对储层分类和地质建模具有重要意义,还有助于储层渗透率的快速评价,例如在核磁共振测井过程中可以基于相应的渗透率预测模型和测井数据直接计算得到储层渗透率[19-21]。
虽然国内外学者提出了许多渗透率预测模型,但这些模型大多是基于对各类常规与非常规油藏的统计、分析得出,对致密砂岩油藏的适用性和预测效果并没有统一的结论,且这些模型大都含有一个或多个模型参数,无法直接应用于油田现场。此外,合理地选择统计误差评价方法对渗透率预测模型的优选至关重要。评价误差的方法有很多,大致可以分为3 类:①相关性评价,如常使用的相关系数R2;②绝对误差评价,如均方根值(RMS);③相对误差评价,如平均绝对百分误差(MAPE)。使用相关性评价方法可以定量分析2 组数据的相关性,但对于计算精度的表征并不适合,而使用绝对误差评价和相对误差评价方法则可以很好地评价计算精度。笔者对选自鄂尔多斯盆地长7 油层组的19 块致密砂岩岩心分别进行高压压汞和核磁共振测试,对比不同岩心渗透率与其他物性参数的关系,并选取4 块具有代表性的岩心对其孔喉分布频率与渗透率贡献率的关系以及核磁共振T2频谱进行对比、分析,明确影响致密砂岩岩心渗透率的关键物性参数,并选取常用的6 种渗透率模型对其预测效果进行分析评价[22],其中选用R2来定量分析影响渗透率的主控因素,选用均方根值和平均绝对百分误差2种误差计算方法来定量评价渗透率预测模型的预测精度,进而优选适用于鄂尔多斯盆地延长组致密砂岩的基于高压压汞和核磁共振的渗透率预测模型,以期对该致密油藏的开发提供有效手段[22-23]。
1 渗透率预测模型
Rezaee 等[24]利用高压压汞和核磁共振测试数据建立了气测渗透率与岩心孔喉半径之间的关系。据文献[16]报道,Winland 等将不同汞注入饱和度下的孔喉半径与气测渗透率关联后提出了Winland模型,并发现气测渗透率与汞注入饱和度为35%时的孔喉半径相关性最好。Swanson[17]引入了与气测渗透率有关的Swanson 因子并提出了Swanson 模型,该因子对应于SHg/pc(汞饱和度/毛管压力)的最大值。Pittman[25]将该最大值对应的孔喉半径称为rapex并提出了Pittman 模型,rapex被视为连通性好的大孔隙与连通性差的小孔隙之间的分界点。Nooruddin 等[26]利用高压压汞测试研究了不同的渗透率预测模型对于碳酸盐岩储层的预测效果。3 种常用的高压压汞渗透率预测模型如表1 所列。

表1 基于高压压汞的渗透率预测模型Table 1 Permeability prediction models based on HPMI data
基于核磁共振预测岩石渗透率的模型主要有Coates 和SDR 模型[27]等。Coates 模型需要测试岩心可动流体体积(FFI)和不可动流体体积(BVI),再结合核磁共振测得的孔隙度计算岩心渗透率[28]。SDR 模型利用T2弛豫时间的几何平均值来预测渗透率[29],相关研究表明,Coates 模型在致密砂岩的渗透率预测中表现得并不是很理想[30]。SDR-REV模型[18]是在SDR 模型的基础上,增加了孔隙度和T2g的指数得到的一种改进模型,由于具有更多的调整参数,因而它比SDR 模型的应用更广,适用性更强,在致密砂岩的渗透率计算中比SDR 模型更加精确,但对于渗透率分布范围大的岩心样品,预测效果将会变差。陈昱林[31]将Kozeny-Carman 公式与T2弛豫时间相结合提出了KCT2w模型,研究表明该模型对特低渗透率的岩石预测效果较好。范宜仁等[32]基于核磁共振双T2cutoff截止值提出了一种致密砂岩渗透率预测方法。常用的基于核磁共振测试的渗透率预测模型如表2 所列。
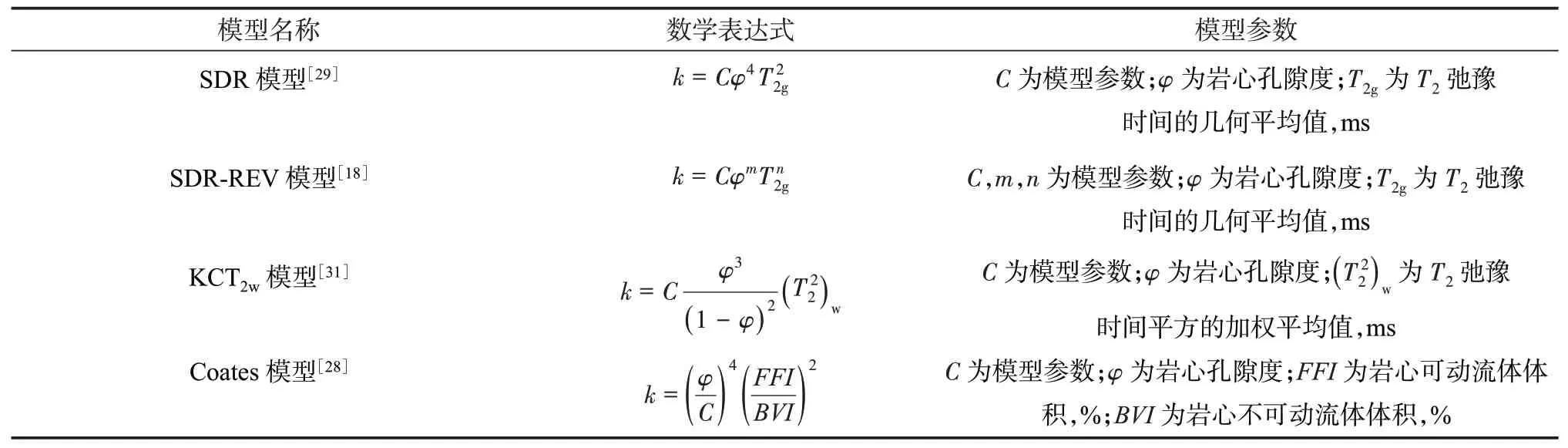
表2 基于核磁共振的渗透率预测模型Table 2 Permeability prediction models based on NMR data
2 实验
选取了来自鄂尔多斯盆地长7 油层组的19 块致密砂岩进行了高压压汞和核磁共振测试[22][图1(a)—(b)]。压汞法的原理是非湿相流体汞在外压的作用下进入岩心,从而得到岩心的孔喉半径等物性参数[33]。核磁共振技术因其对岩心无伤害等优点,已广泛应用于岩心孔隙结构表征[34],其原理是识别岩心中的氢原子。岩石的孔隙结构决定了岩石中的流体分布,基于核磁共振测试得到的T2谱可以区分岩心中可动流体与不可动流体的体积,还可以研究岩心的孔隙结构与流体分布特征[34-35]。所选取的19 块致密砂岩岩心均来自长7 油层组的5 口不同井,取心方式为钻井取心,岩心的成分以石英为主,占总矿物成分的50%以上,其余主要成分包含钠长石、钾长石和黏土,其中钠长石与钾长石体积分数超过20%[22]。表3 为19 块致密砂岩岩心的物性参数表,从表中可以看出,19 块致密砂岩岩心的孔隙度为3.7%~12.2%,平均为8.09%,渗透率为0.005~0.262 mD,平均为0.085 mD,平均孔喉半径为0.028~0.422 μm,平均为0.158 μm,孔喉分布如图1(c)所示。利用核磁共振测试可以得到岩心的孔隙度分布T2图谱,曲线越靠左,表示小孔隙越多;越靠右,表示大孔隙越多。从图1(b)可以看出,所选取的19 块致密砂岩岩心T2时间主要为0.1~1 000.0 ms。
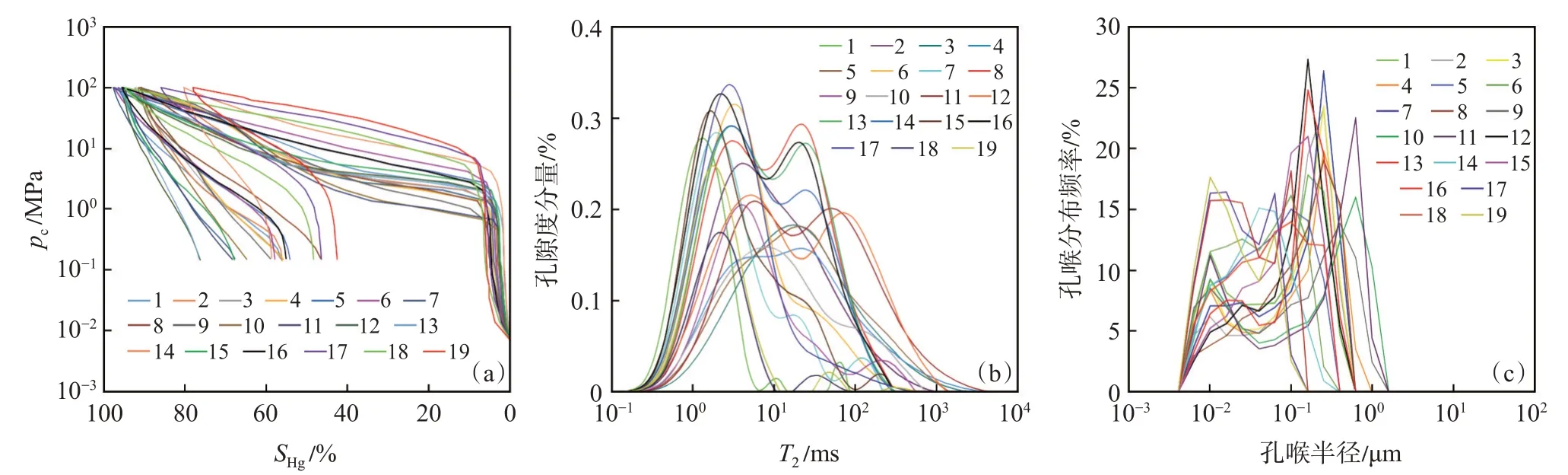
图1 鄂尔多斯盆地延长组致密砂岩岩心毛管压力曲线(a)、核磁共振T2谱(b)和孔喉分布频率(c)(据文献[22]修改)Fig.1 Mercury intrusion capillary pressure curves(a),NMR T2 spectra(b)and pore throat distribution frequency(c)of tight sandstone of Yanchang Formation in Ordos Basin
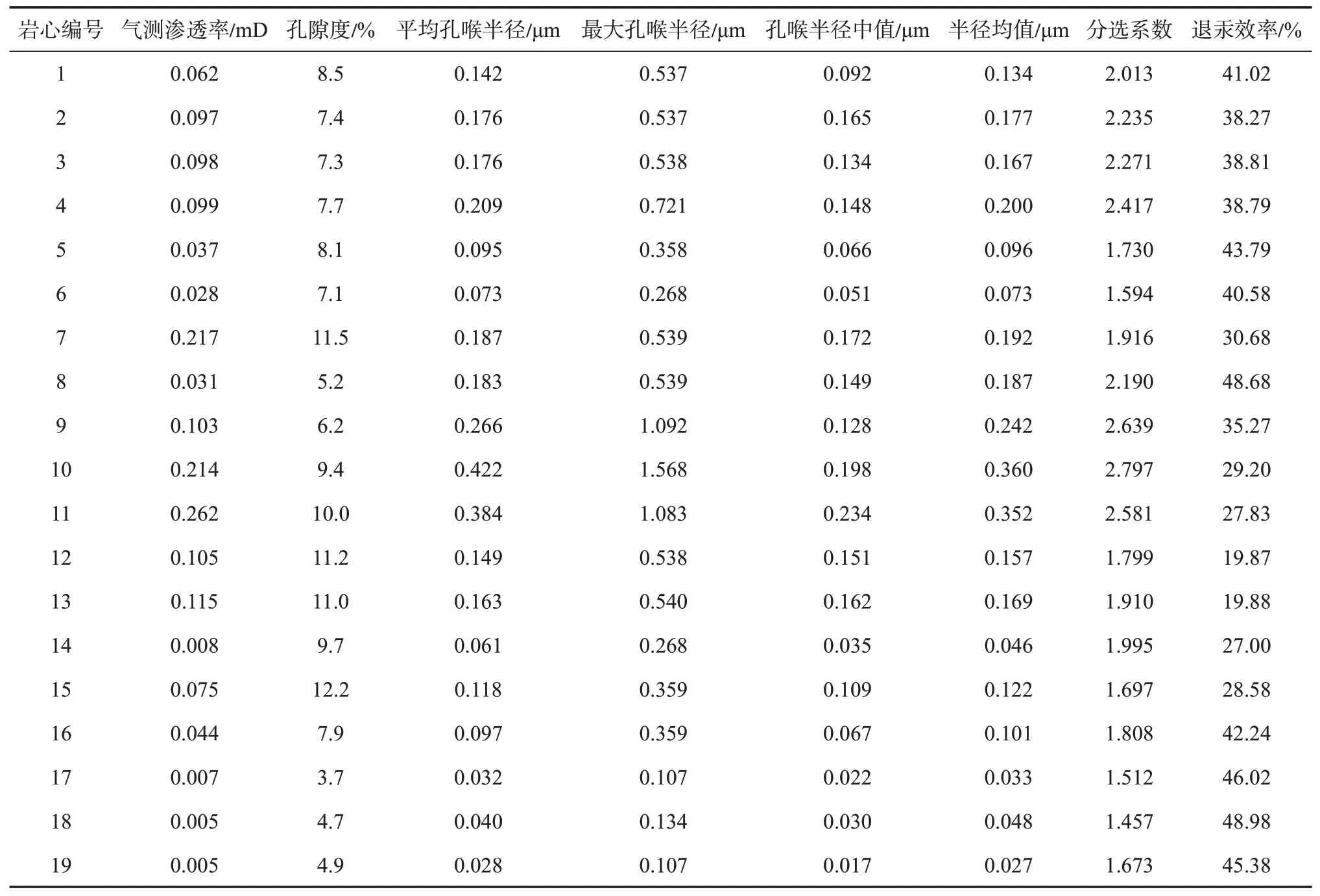
表3 鄂尔多斯盆地延长组致密砂岩岩心物性参数Table 3 Parameters of tight sandstone of Yanchang Formation in Ordos Basin
3 基于高压压汞的渗透率预测
3.1 渗透率模型预测效果评价标准
渗透率模型的预测误差使用均方根值(RMS)和平均绝对百分误差(MAPE)2 种方法进行评价,式(1)和式(2)分别为均方根值和平均绝对百分误差计算公式[26]:

式中:kmeas为岩心样本的实验渗透率,mD;kpred为模型预测渗透率,mD;n为岩心样本的总数,个。
3.2 渗透率与孔隙结构参数的相关性分析
岩石渗透率受多种因素的影响,利用高压压汞测试可以得到岩心的最大孔喉半径、平均孔喉半径、中值孔喉半径、分选系数、退汞效率等物性参数值。图2 为岩心气测渗透率与物性参数交会图,从图2 可以看出,气测渗透率随分选系数、最大孔喉半径、平均孔喉半径、孔喉半径均值、半径均值的增大而增大,随退汞效率的增大而减小,其中,孔喉中值半径与气测渗透率的相关性最好,相关系数为0.899 2,退汞效率与气测渗透率的相关性最差,相关系数为0.338 6,表明致密砂岩岩心的孔喉结构是渗透率的主要控制因素。从图2(f)可以看出气测渗透率与退汞效率呈反比关系,岩心渗透率越小,退汞效率越高。这是由于在压汞测试中,非湿相流体汞首先进入较大的孔喉和连通性好的孔喉,岩心孔喉连通性越差,汞进入的难度越大,因此,对于渗透率低的岩心而言,汞主要存在于大孔喉和连通性好的孔喉中,因而其退汞效率相对更高。对于所选取的19 块致密砂岩岩心,由于岩心的气测渗透率与孔喉半径参数相关性好,则使用基于孔喉半径类参数进行渗透率预测的模型将具有更好的效果。
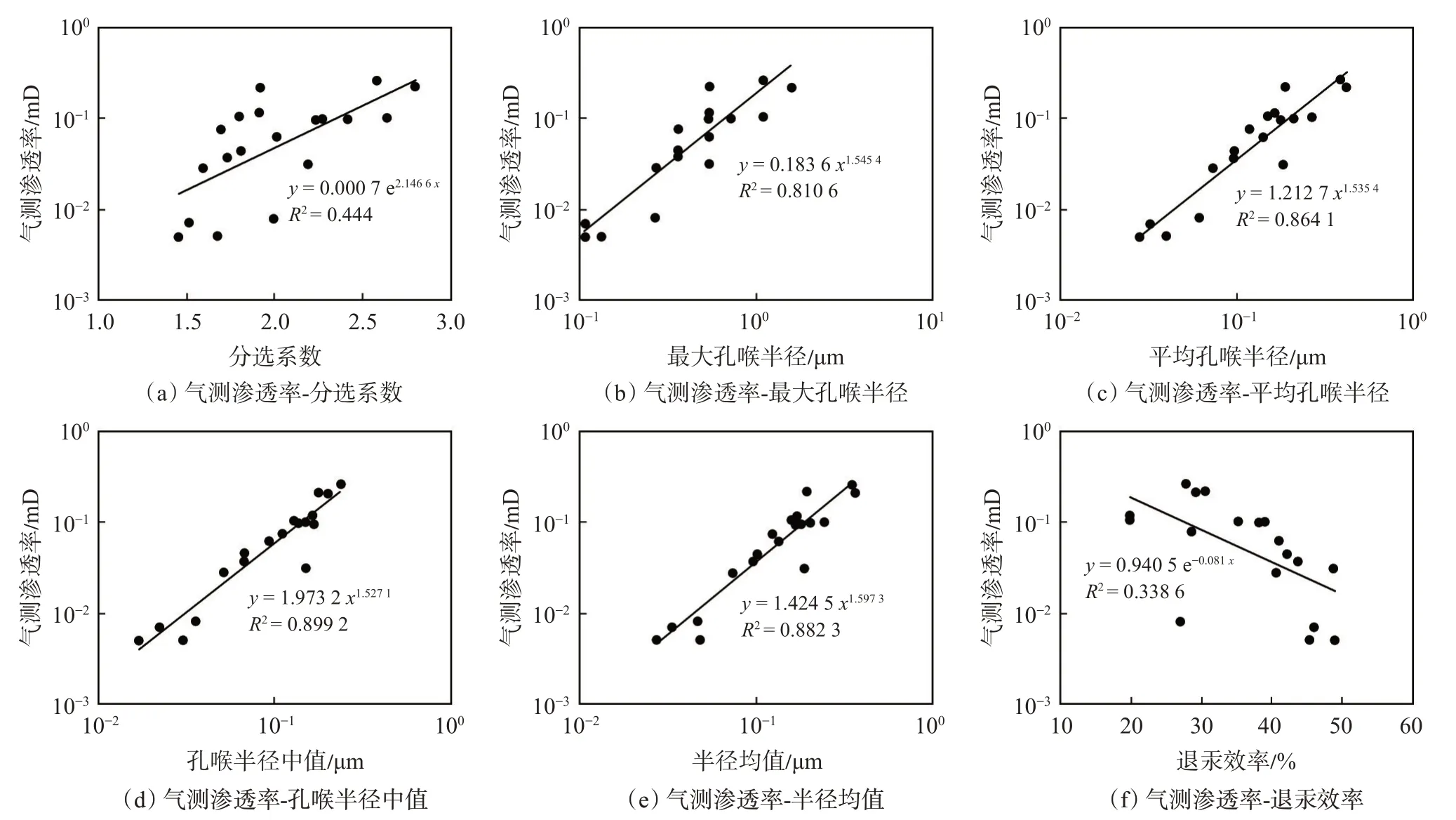
图2 鄂尔多斯盆地延长组致密砂岩岩心气测渗透率与物性参数交会图Fig.2 Correlation between gas log permeability and petrophysical properties of tight sandstone of Yanchang Formation in Ordos Basin
图3 是根据高压压汞测试得到的致密砂岩岩心孔喉分布频率图,从图3 可看出,致密砂岩的孔喉分布为双峰分布,其中左峰的孔喉半径为0.001~0.100 μm,右峰的孔喉半径为0.1~1.0 μm,孔喉半径的渗透率贡献主要取决于右峰,岩心渗透率越大,右峰越接近1 μm。例如图3(a)中样本3 与样本6 具有接近的孔隙度,但样本3 的渗透率明显大于样本6,样本3 的孔喉分布频率的右峰明显比样本6 更接近1 μm;图3(b)中样本11 与样本13 具有接近的孔隙度,但样本11 的渗透率明显大于样本13,样本11 的孔喉分布频率的右峰明显比样本13 更接近1 μm。
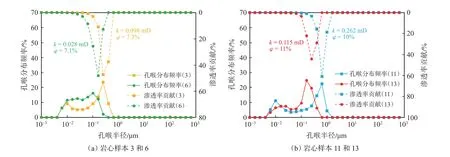
图3 鄂尔多斯盆地延长组致密砂岩的孔喉分布频率与渗透率贡献的关系Fig.3 Relationship between pore throat size distribution and permeability contribution of tight sandstone of Yanchang Formation in Ordos Basin
3.3 基于高压压汞的渗透率预测模型优选与评价
基于Swanson,Pittman,Winland 等模型和高压压汞数据进行了渗透率预测,模型参数通过Origin拟合得到,对不同模型的预测结果进行了定量评价,模型拟合结果与预测误差如表4 所列。图4(a)和(b)分别是基于Swanson 模型和Pittman 模型得到的致密砂岩岩心的气测渗透率与预测渗透率关系图,从图中可以看出,当岩心渗透率为0.1~1.0 mD时,基于这2 种模型得到的致密砂岩岩心渗透率均较准确,当岩心渗透率小于0.1 mD 时,预测的渗透率均稍偏小,其中Swanson 模型的2 种误差计算结果分别为0.030 2 mD 和45.83%,Pittman 模型的2种误差计算结果分别为0.030 9 mD 和60.16%。从图4 还可以看出,基于Pittman 模型得到的岩心预测渗透率与气测渗透率更加接近,但预测精度低于Swanson 模型,分析后认为这是由于2 种模型所使用的岩心参数存在差异所导致,根据前文的分析(参见图2),致密砂岩岩心的气测渗透率与半径类参数具有更好的相关性,而临界孔喉半径正是Pittman 模型所使用的岩心参数之一,这说明在进行渗透率预测时,应根据岩心的物性参数与渗透率的对比关系来合理选择渗透率预测模型。
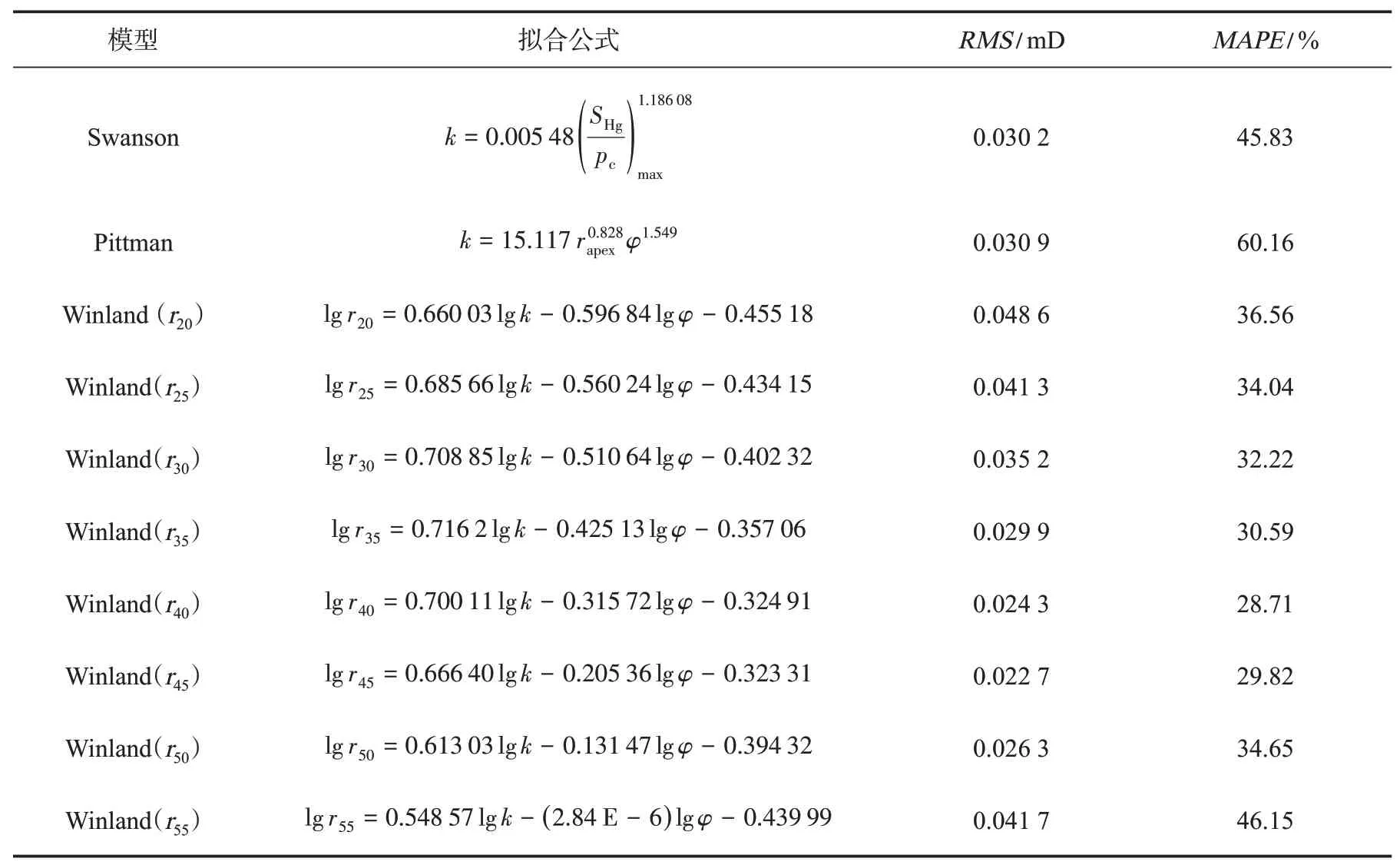
表4 基于高压压汞的渗透率预测模型拟合公式与误差Table 4 Fitting formula and errors of permeability prediction models based on HPMI
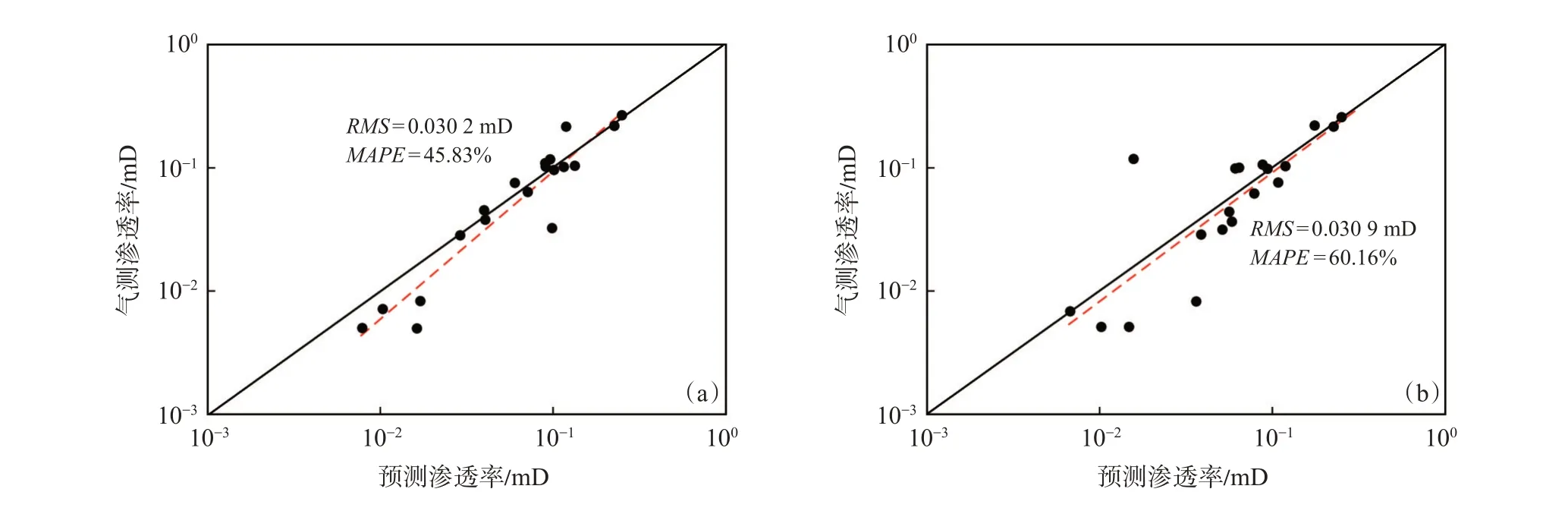
图4 Swanson 模型(a)和Pittman 模型(b)气测渗透率与预测渗透率关系Fig.4 Comparison of predicted permeability with gas log permeability of Swanson model(a)and Pittman model(b)
图5 是基于Winland 模型得到的不同孔喉半径下气测渗透率与预测渗透率关系图,从图5 可以看出,当孔喉半径为r40和r45时,模型预测误差最小,其中基于r40得到的预测渗透率的平均绝对相对误差最小(MAPE=28.71%),基于r45得到的预测渗透率的均方根误差最小(RMS=0.022 7 mD),这一结果并不同于据Winland 模型得到的r35与气测渗透率相关性最好的结论,通过图2 中高压压汞得到的岩心物性参数与气测渗透率对比可以发现,气测渗透率与中值孔喉半径的相关性最好,这证明了本文拟合得到的r40和r45与气测渗透率相关性较好的合理性。
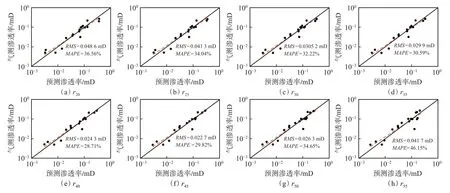
图5 Winland 模型不同孔喉半径下气测渗透率与预测渗透率对比Fig.5 Comparison of predicted permeability with gas log permeability of Winland model under different pore-throat size
4 基于核磁共振的渗透率预测
4.1 核磁共振主要参数与渗透率的相关性分析
核磁共振T2谱的分布代表着岩心孔隙的分布,通过研究T2时间与渗透率的关系可以得到岩心孔隙与渗透率的关系。T2几何平均值是指利用不同孔隙度分量与对应的弛豫时间乘积的核磁孔隙度次方根求得的几何平均值,常用于渗透率模型进行渗透率计算等;T2加权平均值是一种位置特征参数,能够描述核磁共振全孔隙分布的平均位置,可利用核磁共振T2弛豫时间与孔隙度分量乘积再除以核磁孔隙度得到[36]。图6 为核磁共振测试T2图谱中T2几何平均值、T2加权平均值与气测渗透率对比图,从图6 可以看出,致密砂岩气测渗透率与T2几何平均值和T2加权平均值的相关系数分别为0.830 2 和0.693 5,气测渗透率与T2几何平均值的相关性更好,这表明对于本文所选取的19 块致密砂岩岩心,对同一模型使用T2g进行渗透率预测的结果将优于T2w。
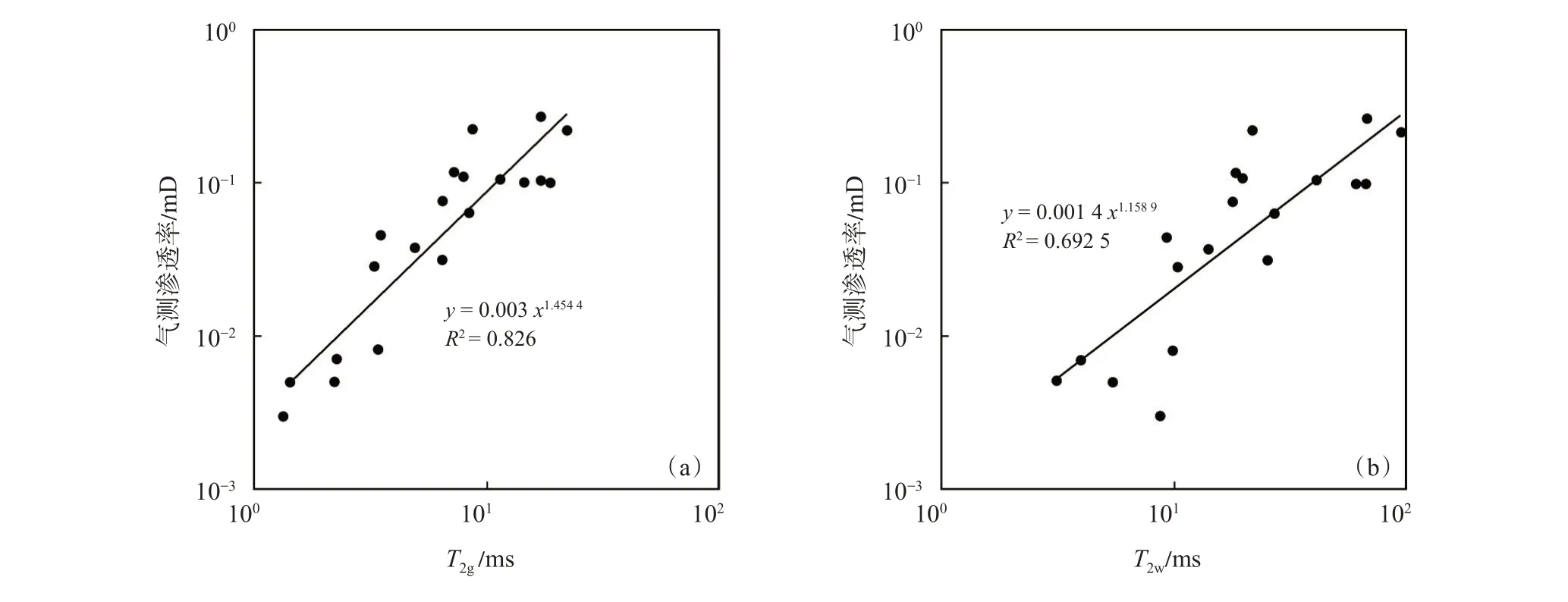
图6 鄂尔多斯盆地延长组致密砂岩岩心气测渗透率与T2几何平均值(a)和T2 加权平均值(b)的关系Fig.6 Relationship of gas log permeability with T2 geometric mean(a)and T2 weighted mean(b)of tight sandstone of Yanchang Formation in Ordos Basin
图7 是通过核磁共振测试得到的岩心饱和状态T2频谱分布与饱和状态T2累计分布曲线,从图7 可以看出,致密砂岩的核磁共振T2频谱多为双峰或三峰分布,左峰主要集中在0.1~10.0 ms,右峰主要集中在10~1 000 ms,对于孔隙度接近而渗透率相差较大的岩心,渗透率较大岩心的饱和状态T2频谱分布与饱和状态T2累计分布曲线明显比渗透率较小的岩心更靠右,如图7(a)中3 号岩心与6 号岩心的孔隙度相差0.2%,而3 号岩心的渗透率(0.098 mD)却是6 号岩心(0.028 mD)的3.5 倍,3 号岩心的饱和状态T2频谱分布与饱和状态T2累计分布曲线明显比6 号岩心更靠右,说明3 号岩心比6 号岩心的大孔占比更高;图7(b)中11 号岩心与13 号岩心的孔隙度相差1%,而11 号岩心的渗透率(0.262 mD)却是13 号岩心(0.115 mD)的近2.3 倍,11 号岩心的饱和状态T2频谱分布与饱和状态T2累计分布曲线明显比13 号岩心更靠右,说明11 号岩心比6 号岩心的大孔占比更高,这些均表明,对于致密砂岩而言,孔喉结构特征对渗透率的影响大于孔隙度对渗透率的影响。
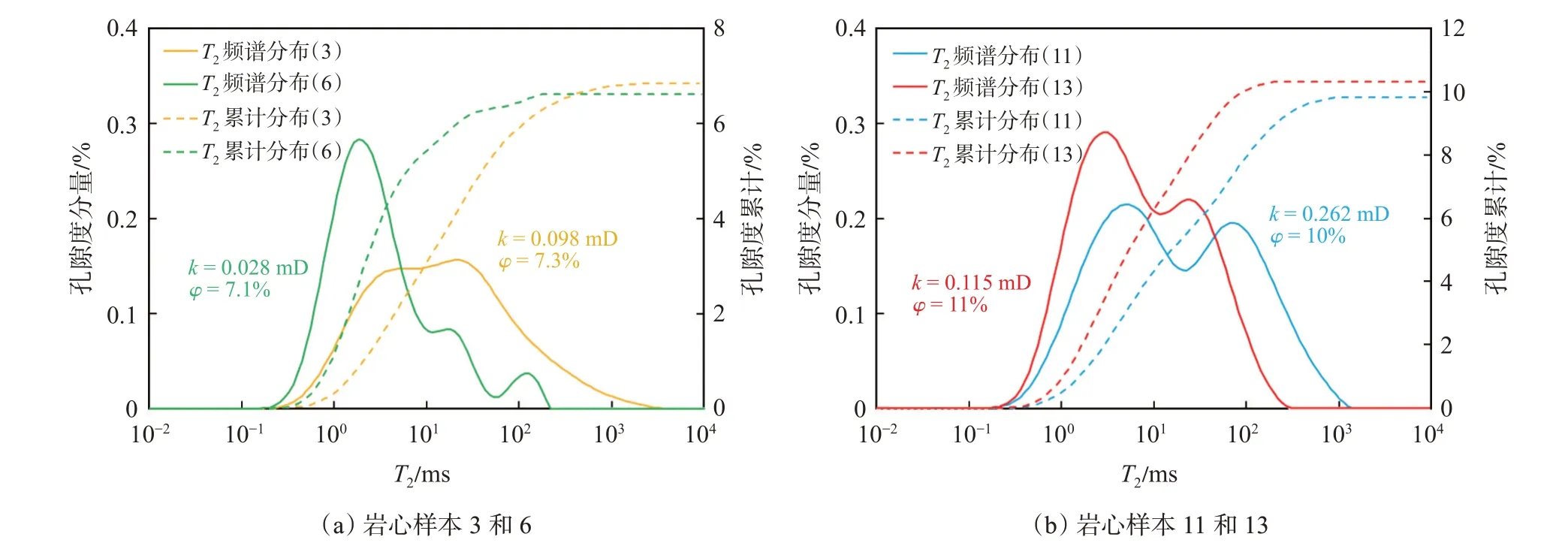
图7 鄂尔多斯盆地延长组4 块致密砂岩岩心的核磁共振测试T2 频谱分布曲线对比Fig.7 NMR T2 spectra curve of four tight sandstone cores of Yanchang Formation in Ordos Basin
4.2 基于核磁共振的渗透率预测模型优选与评价
基于SDR,SDR-REV,KCT2w和KCT2g模型以及核磁共振数据进行了渗透率预测(表5),并对预测结果进行了定量评价,模型预测精度通过式(1)—(2)进行计算。图8 是分别基于SDR,SDR-REV,KCT2w(基于T2加权平均值T2w)及KCT2g模型(基于T2几何平均值T2g)的渗透率预测结果与气测渗透率的对比图,从图8 可以看出,利用SDR-REV模型计算得到的致密砂岩渗透率与实验气测渗透率具有较好的一致性,计算误差最小。其原因为SDR-REV 模型具有更多的调整参数,这使得模型的预测范围更加广泛,预测精度更高。SDR,KCT2g,KCT2w等模型预测结果偏大,且岩心越致密,渗透率预测相对误差越大。其原因可能是岩心渗透率越低,气体滑脱效应越明显,模型预测的渗透率更接近于岩心克式渗透率,与岩心气测渗透率差异增大。对比图8(c)和(d)可知,相比于KCT2w模型,使用KCT2g模型进行渗透率预测的误差更小,其原因是与T2w相比,T2g与气测渗透率具有更好的相关性(参见图6)。
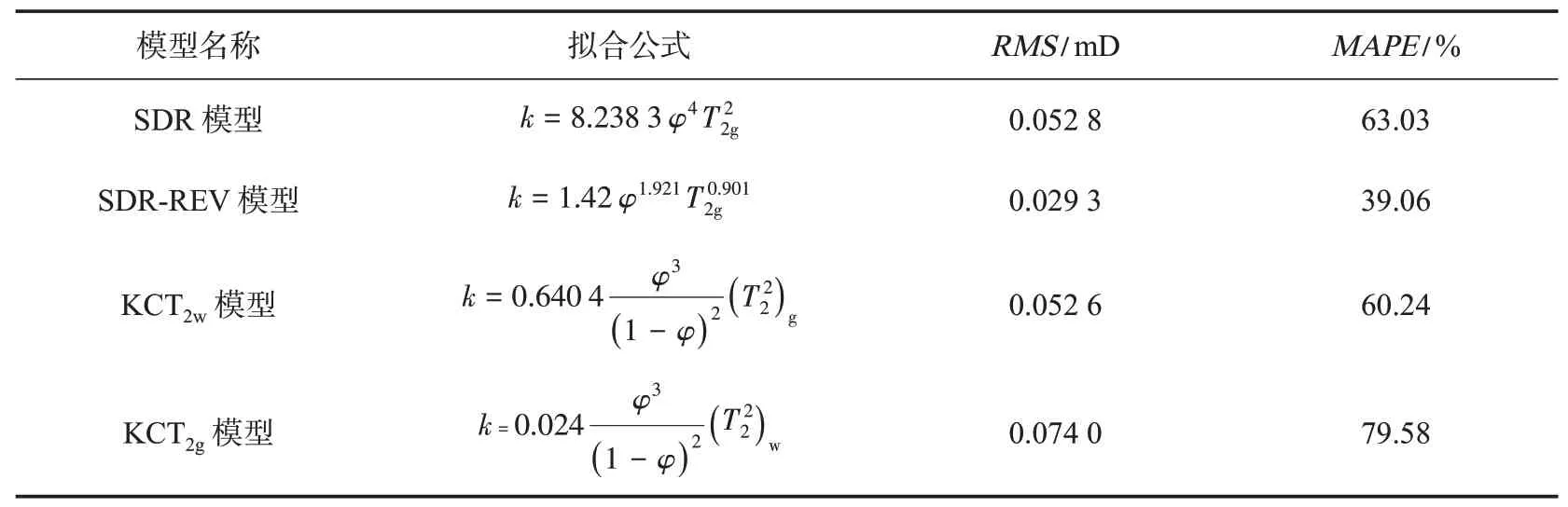
表5 基于核磁共振的渗透率预测模型拟合公式与误差Table 5 Fitting formula and errors of permeability prediction models based on NMR
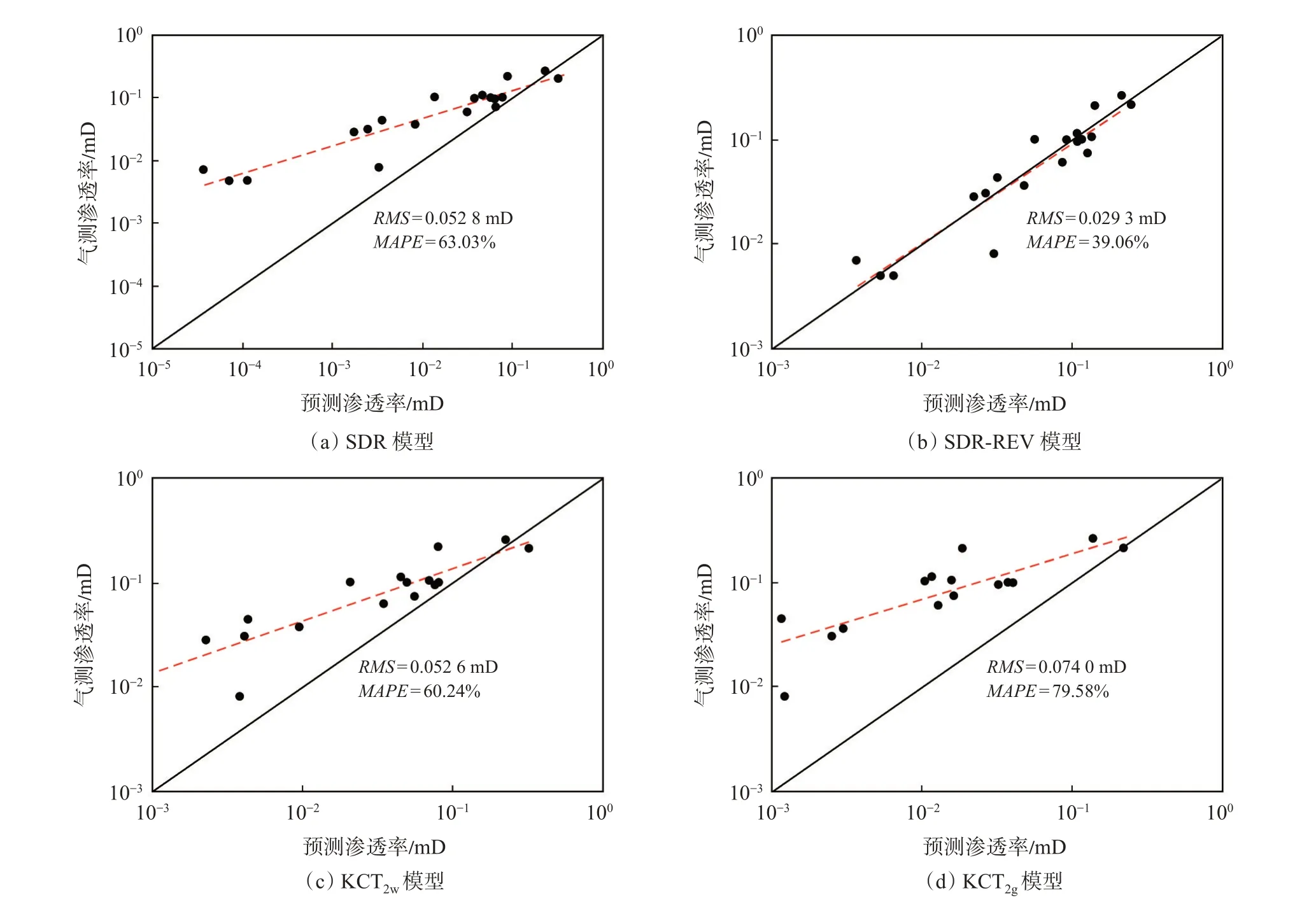
图8 基于核磁共振数据的模型气测渗透率与预测渗透率对比Fig.8 Comparison of predicted permeability with gas log permeability based on NMR data
5 结论
(1)对选自鄂尔多斯盆地长7 油层组的19 块致密砂岩岩心进行了高压压汞和核磁共振测试,并对6 种渗透率预测模型的预测效果进行了评价。在核磁共振测试数据中,相比于T2加权平均值,T2几何平均值与气测渗透率的相关性更高;在通过高压压汞测试得到的岩心物性参数中,孔喉半径中值与气测渗透率的相关性最好。
(2)在基于SDR,SDR-REV,KCT2w模型和核磁共振数据的渗透率预测结果中,SDR-REV 模型的预测精度最高;对于KCT2w模型,使用T2几何平均值预测的渗透率精度高于T2加权平均值。
(3)在基于Swanson,Pittman,Winland 模型和高压压汞测试数据的渗透率预测结果中,Winland模型的预测结果优于Swanson 和Pittman 模型;在Winland 模型中,r40和r45与气测渗透率的相关性较好,预测的渗透率精度较高。
(4)对于鄂尔多斯盆地延长组致密砂岩,基于核磁共振数据进行渗透率预测时选用SDR-REV 模型效果最佳,基于高压压汞数据进行渗透率预测时使用Winland 模型中r40与r40预测的精度较高。
