进给系统成对安装的角接触球轴承热分析

赵春雨， 侯森林， 李朕均

(东北大学 机械工程与自动化学院， 辽宁 沈阳 110819)

随着国内制造业的发展越来越迅速，对加工精度的要求越来越高，因此提高机床的加工精度以及工作稳定性是促进机床发展的关键.滚珠丝杠广泛用于机床等各类精密设备中，通常加工精度在很大程度上会受到系统温升的影响，而轴承温升占很大一部分，所以，对丝杠轴承进行温度分析具有重要意义.而机床进给系统的几个主要热源中轴承发热量最大，也就是对滚珠丝杠等关键进给部件的影响最大，所以对丝杠轴承进行热分析在研究机床进给系统热误差中具有重要意义.

Palmgren[1]采用试验方法推导出计算轴承摩擦力矩的经验公式.Bossmanns等[2]建立了高速电主轴的有限差分热分析模型.Lin等[3]研究了轴承预紧力对轴承刚度的影响，分析高速旋转效应下离心力和陀螺力矩对主轴的影响.Xu等[4]基于有限元方法对机床主轴系统进行温度分析，考虑接触热阻和热功率随着温度变化带来的影响，并对机床壳体系统的热膨胀进行分析.Pouly等[5]建立了油-气润滑推力球轴承的热网络模型，预测了推力球轴承的功率损失和温度分布.Ma等[6]运用热网络法研究脂润滑圆柱滚子轴承瞬态温度场，并分析不同转速及润滑脂填充量的温度变化.Zheng等[7]分析轴承热特性时充分考虑了润滑剂、径向和轴向结构约束和装配约束，提出了一种新的角接触球轴承多节点热网络模型.

本文建立了进给系统轴承的瞬态热网络模型，基于隐格式差分法，推导出网络各节点温度计算的递推算法，并通过试验进行了验证.

1 轴承系统的热源发热率计算

1.1 轴承运动分析

外圈滚道曲率中心B及轴承运行前后内圈滚道曲率中心C和C′位置如图1所示.O与O′分别为轴承运行前后滚珠中心；δr，δa分别为轴承内外圈中心径向和轴向位移，αij，αoj分别为滚珠与内外圈的接触角.

由图可知：

A1j=Asinα+δa+θRicosψj，

(1)

A2j=Acosα+δrcosψj.

(2)

其中：α是轴承的初始接触角；ψj为滚珠角位置；θ为角位移；Ri为内圈滚道曲率中心相对于轴承轴线的距离.

几何协调方程为

(3)

滚珠所受载荷如图2所示，滚珠的法向载荷与法向接触变形的关系为

(4)

(5)

其中，Kij和Koj是内外圈的弹性变形系数，与相互接触的材料属性和几何形状有关，由赫兹接触理论求出.

对图建立水平和垂直方向上力的平衡方程:

(6)

(7)

在只受轴向力作用时，整个轴承的受力平衡方程：

(8)

联立式(3),式(6)～式(8)五个非线性方程对未知量δa，δij，δoj，X1j，X2j进行求解，求解采用牛顿-拉弗逊法.根据求解得到的变形量可求解轴承在工作期间滚珠与内外圈的接触角.

1.2 发热率计算

轴承引起的功率损失为摩擦力矩与轴承转速的乘积.轴承总的摩擦力矩由接触区域的轴承摩擦力矩M和滚珠与沟道接触的自旋摩擦力矩Ms组成[1]，即轴承的发热量为

(9)

其中:H为单位时间发热量；n为轴承转速；Ms为滚珠与滚道之间的自旋摩擦力矩；ωs为滚珠的自旋角速度.

摩擦力矩M是由两部分组成：

M=M1+M2.

(10)

M1为与轴承负荷有关的项:

M1=f1P1dm.

(11)

其中:f1为与轴承类型和所受负荷有关的系数；P1为确定轴承负荷；dm为轴承节圆.

M2为黏性摩擦力矩：

(12)

其中:fo为与轴承类型和润滑方式有关的系数；vo为工作温度下润滑剂的运动黏度.

依据琼斯的沟道控制理论[8]：滚珠在与轴承内、外圈接触过程中，在一个滚道上同时存在滚动和自旋，而在另一个滚道上作纯滚动.对于高速球轴承，由于离心力的作用，轴承为外滚道控制，滚珠在外滚道上运动为纯滚动，即自旋分量Mso=0.在此仅考虑球体与内滚道之间的自旋摩擦力矩Msi:

(13)

其中:Qi为滚珠与滚道之间的法向载荷；μi为摩擦系数；a为接触椭圆的长轴长度；ε为第二类椭圆积分.

球与内圈接触的自旋角速度为

ωsi=-ωbsin(β-αi)+(ω-ωc)sinαi.

(14)

其中:ω为轴的角速度；ωb为滚珠的自转角速度；ωc为滚珠的公转角速度；αi为球与内滚道的接触角；β为姿态角[9].

(15)

(16)

(17)

其中:γ′=Dw/dm;Dw为滚珠直径.

在工作过程中，轴承摩擦力矩产生的热一半进入滚动体，另一半进入轴承内外圈；而滚珠与沟道的自旋摩擦力矩产生的热平均分配到滚动体和轴承内圈中[10].

2 轴系热网络分析模型

2.1 热节点布置

依据轴承系统结构，选择典型的温度节点建立其热网络.节点之间阻碍热量交换的阻力设为热阻，依据轴系结构和材料参数确定各热阻值，计算轴承瞬态温度场.本文建立具有9个温度节点的数控机床进给系统丝杠轴承热网络，轴承系统的结构及温度节点的布置如图3所示.“①”代表节点1位置，其余类推.热温度节点定义和连接方式如表1和表2所示.

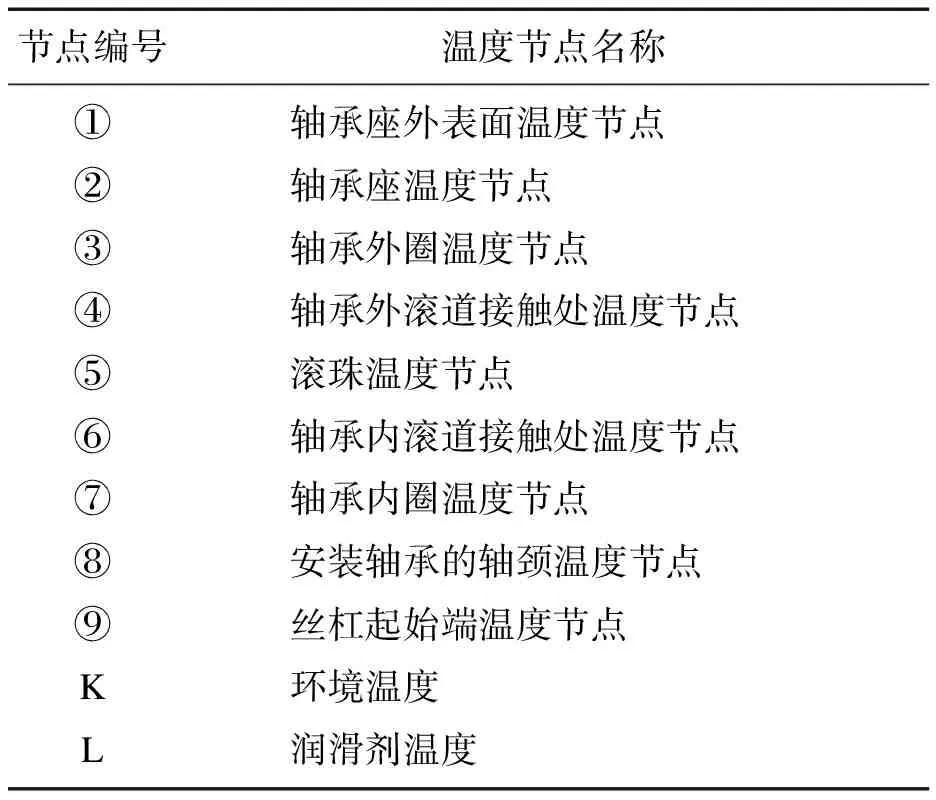
表1 轴承系统温度节点定义

2.2 热传递分析

热传导、热对流和热辐射是轴承热传递主要

表2 温度节点间的热传导关系

形式.热辐射对轴承元件之间的热传递影响很小，可以忽略热辐射影响[11].在工作过程中，轴承座、轴承内外圈、滚珠、丝杠阶梯轴之间发生热传导.在此，将轴承内外圈和轴承座简化为圆筒，丝杠阶梯轴简化为圆柱.若仅考虑其径向热传递，可处理为一维热传导模型，其热阻值为

(18)

其中:λ为物体的导热系数；Ls为物体的特征长度；A为物体导热面积.

轴承座的外表面与空气之间产生自然对流换热，旋转的丝杠轴与空气之间发生强制对流换热,在轴承内部，热量也在轴承零件和润滑脂之间传递.

热对流阻值计算模型为

(19)

其中:hv为对流换热系数；Nu为无量纲的Nusselt数；K为流体的导热系数；A为物体壁面面积；L为物体对流换热特征长度.

以上传导热阻及对流换热热阻经过多年试验及理论研究总结出大量经验公式，根据换热的具体情况，通过查表得到零件材料及尺寸参数，选取相应的经验公式进行计算[8,11].

2.3 结合面接触热阻

结合面的接触阻力表示[12]为

(20)

其中:A为接触区域的表观接触面积;hc为接触导热系数.

轴承外圈与轴承座孔的结合一般采用间隙配合，其接触导热系数为

(21)

其中:λring和λair分别为轴承外圈和空气的导热系数；hring，hgap分别为轴承外圈和周向空气厚度[2].

轴承内圈与丝杠轴表面的接触导热系数为

(22)

其中:Lg是两个接触面的空隙厚度；Ac是接触处的真实接触面积；Av为接触处的空气面积；k1，k2，kf分别是两部分接触材料及空气的导热系数.接触导热系数的具体数值见表3.

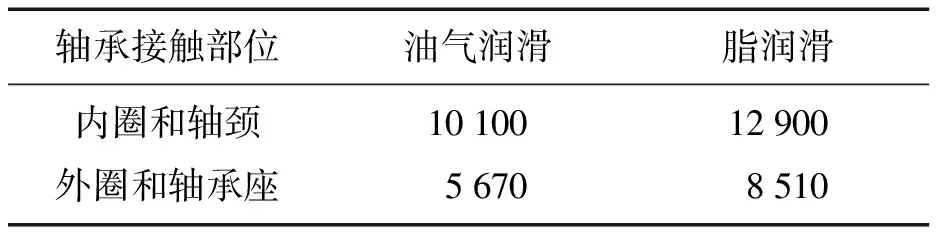
表3 结合面接触导热系数[11]

2.4 瞬态平衡方程建立

节点的能量变化满足热流平衡原理，在热平衡之前，每个节点流入的热流量等于流出的热流量.图4为一个节点上的对流与传导热流示意图.

根据热通量平衡原理，节点i的瞬态温度平衡方程可以表示为

(23)

其中:qi为节点i热流量;ρi为节点i材料密度;cpi为材料的比热容;Vi为节点i相关材料体积;Ti为节点i的温度;dTi/dt为节点i处的温升率.

利用一阶差分格式，则

(24)

其中，Δtk=tk+1-tk是计算的步长.

对于式(23)，右端传热项在[tk,tk+1]区间内传热值取为两时间点的均值，即

(25)

将式(24)、式(25)代入式(23)得

(26)

其中:Ci=cpiρiVi;Δhij=Δt/(2Rij).

利用表2，依据式(24)～式(26)，推导出系统温度变化的计算方程组为

AXk+1=BXk+D.

(27)

依据表2，节点1和9无热源，与环境热交换，而变量X中含环境变量，将其并入D中，则

d1=TK/R1K，d9=TK/R9K.

节点2,3和7,8无热源，其值皆为0，即

d2=d3=d7=d8=0.

节点5为滚珠，与内外圈接触摩擦生热，存在两个热源，分别记为q5i和q5e；同时，与油膜间存在热交换.若滚珠与内外圈接触生热的50%传入滚珠，则

d5=TL/R5-L+0.5q5i+0.5q5e.

内外圈4和6也与油膜产生热交换，即

d4=TL/R4-L+0.5q5i，d6=TL/R6-L+0.5q5e.

3 试验及计算结果

试验机床型号为HTC 2050i，具体试验设备有： PC104总线工业控制计算机；铂热电阻温度传感器4个；红外热像仪1台；激光干涉仪1台；笔记本电脑2台，1台用于记录温度传感器测量的温度数据，1台用于记录激光干涉仪测量的误差数据.具体试验设备如图5所示[9].

Z轴进给系统轴承为NSK公司的25TAC62B滚珠丝杠专用轴承，轴向预紧力为1 kN.当电机转速为500,1 000和1 500 r/min时，对进给系统工作过程远离电机的轴承表面温度进行了测试.测试温度分为系统工作和自然冷却两个阶段.

利用上述热网络算法对轴承温度进行了计算，计算过程润滑剂黏度随温度变化规律按表4数据线性插值处理.对应热阻值根据图纸结构和材料参数确定.图6为计算与试验结果的对比.由图6可见，模型预测与试验测试最大误差值1.3 ℃，出现在进给速度1 500 r/min，机床工作40 min时，模型预测温度为36.9 ℃，试验测量温度为35.6 ℃.此试验结果证明了本文热网络算法的有效性.

表4 润滑剂的黏温特性[4]

图7为进给电机转速1 000 r/min时轴承各节点温度随工作时间的变化.由图7可见，轴承各节点温度随时间推移呈指数上升，并在轴系达到热平衡后趋于稳定.模型预测最高温度在轴承内滚道，这与实际工况相吻合；停机后轴承内滚道温度冷却速度最快，这是由于轴承密封方式为直通式迷宫密封，停机后轴承内空气与外界相通，润滑剂冷却速度较快导致.当机床停机之后，丝杠轴端温度有小幅度的上升，这是由于停机初始阶段高温区的热量传过丝杠轴端，停机后丝杠轴与空气为自然对流散热，故符合轴承工作情况.图8为不同进给速度时轴承节点温升曲线比.由图可见，轴承内滚道温升比外滚道迅速，温度随进给系统的转速增加而升高.

4 结 论

1) 基于进给系统轴承特点，考虑接触热阻及润滑剂黏温效应的影响，建立成对安装角接触球轴承瞬态热网络模型，并给出考虑轴承自旋摩擦力矩的轴承生热计算模型.

2) 基于热网络中单节点换热过程的微分方程，推导出轴承系统温度场的隐格式差分方程组的计算方法，描述轴承热网络节点温度的时变规律.

3) 利用本文计算方法，计算出了进给系统工作过程轴承温度随时间的变化，并通过试验验证了其有效性；通过数值计算，分析了进给速度对轴承系统各节点时变特性的影响.