Docking control for probe-drogue refueling: An additive-state-decomposition-based output feedback iterative learning control method
2020-05-21JinruiRENQunQUANCunjiLIUKiYunCAI
Jinrui REN, Qun QUAN, Cunji LIU, Ki-Yun CAI
a School of Automation Science and Electrical Engineering, Beihang University, Beijing 100083, China
b Department of Aeronautical and Automotive Engineering, Loughborough University, Leicestershire LE11 3TU, United Kingdom
KEYWORDS Additive state decomposition;Adjoint operator;Docking control;Iterative learning control;Probe-drogue refueling;Stable inversion
Abstract Designing a controller for the docking maneuver in Probe-Drogue Refueling(PDR)is an important but challenging task, due to the complex system model and the high precision requirement. In order to overcome the disadvantage of only feedback control, a feedforward control scheme known as Iterative Learning Control (ILC) is adopted in this paper. First, Additive State Decomposition (ASD) is used to address the tight coupling of input saturation, nonlinearity and the property of NonMinimum Phase (NMP) by separating these features into two subsystems (a primary system and a secondary system). After system decomposition, an adjoint-type ILC is applied to the Linear Time-Invariant(LTI)primary system with NMP to achieve entire output trajectory tracking, whereas state feedback is used to stabilize the secondary system with input saturation. The two controllers designed for the two subsystems can be combined to achieve the original control goal of the PDR system. Furthermore, to compensate for the receiverindependent uncertainties, a correction action is proposed by using the terminal docking error,which can lead to a smaller docking error at the docking moment. Simulation tests have been carried out to demonstrate the performance of the proposed control method, which has some advantages over the traditional derivative-type ILC and adjoint-type ILC in the docking control of PDR.©2019 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
1. Introduction
Autonomous Aerial Refueling(AAR)is an important method to increase the voyage and endurance of Unmanned Aerial Vehicles (UAVs) and avoid the conflict between the takeoff weight and the payload weight1,2. Among the aerial refueling methods in operation today, the Probe-Drogue Refueling(PDR)3is the most widely adopted one owing to its flexibility and simple requirement for equipment.There are five stages in the process of PDR,and docking is the most critical and difficult stage because it is more susceptible to disturbances,which directly affects the success of AAR. The docking control task is to control the probe on the receiver to link up with the drogue for fuel transfer.The docking control for PDR is a difficult task for two main reasons.First,the system model in the docking stage is a Multi-Input-Multi-Output(MIMO)higher-order nonlinear system with nonminimum-phase, multi-agent, and multi-disturbance features, which is complex for control design. Moreover, the receiver dynamics is slower than the motion of the drogue, and so it is hard for the probe on the receiver to capture the moving drogue. The second reason is that the precision requirement for the PDR docking control is high. Concretely, the docking error should be controlled within the centimeter level, and the relative velocity between the probe and the drogue should be controlled within a small range,such as 1.0-1.5 m/s1,4.Therefore,the docking controller design for PDR is important but challenging.
Most existing docking control methods for PDR mainly focus on feedback control,such as Linear Quadratic Regulator(LQR)5,6, NonZero SetPoint (NZSP)7,8, Active Disturbance Rejection Control (ADRC)9, adaptive control10,11, backstepping control12,13, etc. Feedback control methods are likely to result in a chasing process between the receiver and the drogue,which may cause overcontrol. Besides, the chasing action may lead to certain impact and damage to the drogue and the probe, which is dangerous and needs to be avoided according to ATP-56(B)issued by NATO(North Atlantic Treaty Organisation)4.Under this circumstance,Iterative Learning Control(ILC) attracts the researchers’ attention. ILC14is an effective cycle-to-cycle feedforward control approach to achieve entire output trajectory tracking within a given time interval.It often applies to systems that repeat the same operation over a finite trial length 0 ≤t ≤T. The repeatability of the considered system can be utilized to improve the system control performance via the ILC method. For the docking of the PDR system, if a docking attempt fails, the receiver will retreat to the standby position for the next attempt, as shown in Fig. 1, where k is the cycle number.That means the docking process is repetitive.Thus, ILC is a good choice to solve the docking control problem15.
The tool of system inversion plays a crucial role in the classical ILC design to approach perfect tracking16. However, for a NonMinimum Phase (NMP) system, the common system inversion is unstable. Thus, many special ILC designs for NMP systems were proposed. Stable inversion is a noncausal method to solve the tracking problem for NMP systems17,18by avoiding the influence of the unstable zeros of the system. However, completely accurate information about the system is required. Therefore, if there exists any uncertainty about the system,then the conventional stable inversion method cannot be applied directly19.Based on the stable inversion, an adjoint-type ILC is proposed20-26, which employs the adjoint operator to make the input to approach the stable inversion19. Because of its online iterative process, the controller can deal with uncertainties,and obtain a better tracking result than that obtained by the conventional stable inversion method.
Because the receiver dynamics is a typical NMP system,PDR systems are a class of nonminimum phase nonlinear systems with input saturation, and the main difficulty of solving the docking control problem for PDR is caused by the tight coupling of input saturation, nonlinearity and the property of NMP. There are some mature methods to deal with these features separately.However,for the systems with all the three features coupled,adopting existing methods may lead to complex computation and low convergence speed. For docking control, it is expected that the docking should be completed as quickly as possible, for example within 2-3 docking attempts. In order to address the problem, a method called Additive-State-Decomposition-Based (ASDB) ILC is proposed in this work. Through Additive State Decomposition27,28(ASD), a kind of system separation method, the influence of NMP is separated to a subsystem named primary system, and the input saturation and nonlinearity features are left to the other subsystem named secondary system. Then,designing controllers for these two subsystems is easier than designing a controller for the original PDR system.

Fig. 1 Repetitive docking operation in aerial refueling.



Fig. 2 Coordinate frames for PDR system.

Fig. 3 Three views of PDR system.

During the docking stage,the docking moment is defined as

then the docking is viewed as successful, where vd,x∈R is the drogue velocity in the direction of the X axis of the tanker frame otxt,vp∈R is the velocity of the front-end of the probe,vmax,vminare the threshold of relative velocity to open the fuel valve at the docking moment,and rdis the radius of the drogue as shown in Fig. 3.
2.2. ILC problem statement
According to Section 1, ILC is a preferable way to solve the docking control problem. A comprehensive model for the PDR system is described as Eq.(6).For PDR systems,the drogue dynamics is passive and uncontrollable.Thus,the receiver aircraft (1) is focused and rewritten as a model for ILC controller design:
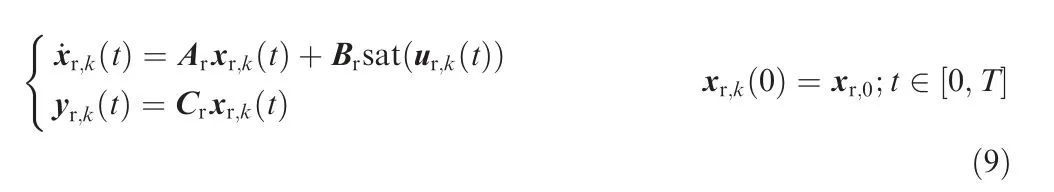
where t ∈ [0 T ] is the time with the cycle period T, the subscript k ∈N+is the cycle number. The system matrix Aris stable, system (9) is a nonminimum-phase nonlinear system with input saturation,and its relative order is r,xr,0represents the initial condition, which can be measured by various types of sensors, for example, vision-based systems. The following preliminary assumptions are made on system (9).
Assumption 1. The reference trajectory yr,dsatisfies


that ur=ur,dmakes yr=yr,d, where ui,min<ur,d,i(t )<ui,max(i =1,2,3) on [ 0 T].system (9), such that
Control objective.Construct a sequence of control ur,k(t )for

where yr,k(t ) is the corresponding output driven by ur,k(t ).
Remark 1. Assumption 2 means that there exists a desired input ur,dwithin the actuating ability of actuators. If such an input ur,ddoes not exist, then the desired output cannot be achieved and needs to be redesigned.
Remark 2. Assumption 1 is a necessary condition of Assumption 2, because, in the process of system inversion, the r-order time derivative of the reference trajectory yr,dneeds to be calculated.If yr,dis not smooth enough,then the derivative will become infinite, and leads to that ui,min<ur,d,i(t )<ui,max(i =1,2,3) does not hold.
Remark 3. Although the proposed method in this paper requires that the system information, namely the matrices Ar,Br,Crare known, it is an online iterative method, and it can deal with the system uncertainties. The system output can converge to the reference trajectory quickly even when there exist uncertainties. The simulation results in Section 4 will show the details.
For an actual PDR system,the drogue position and the relative position between the probe and the drogue are usually measured by vision-based sensors31,32whose measurement precision depends on the relative distance(higher precision in the closer distance).Therefore,compared with the trajectory data,the terminal positions of the probe and the drogue are usually easier to measure in practice. Filters can also be used to remove the sensor noise.
Noteworthy, the reference trajectory yr,d(t ) and the initial iterative input ur,1(t ) can be achieved from historical experience (previous tasks), or through some theoretical methods including low-pass filter method33, polynomial interpolation method6, terminal guidance method34, and iterative optimization method.
3. ASDB ILC controller design
In order to cope with the uncertainty from receiver-related and receiver-independent reasons, the controller design is divided into two steps. The first step is to design an ILC controller for the receiver system(9)based on ASD and adjoint operator.The second step is to introduce a correction term based on adjoint operator and integrated system (6). The receiverrelated uncertainties can be diminished in the first step, while the receiver-independent uncertainties can be attenuated in the second step.
3.1. ILC based on ASD and adjoint operator
In this part, only the receiver is considered. By using ASD27,28, the considered NMP nonlinear system (9) is decomposed into two systems: an NMP LTI system (12)as the primary system, together with a nonlinear system(15) with input saturation as the secondary system. Since the output of the primary system and the state of the secondary system can be observed, the original ILC problem for system (9) is correspondingly decomposed into two subproblems: an output feedback ILC problem for an NMP LTI system and a state feedback stabilization problem for a nonlinear system with input saturation. Thanks to the ASD, the ILC problem is independent of nonlinearity and input saturation. As a result, the two new subproblems are much easier than the original problem for the nonlinear NMP system with input saturation.
3.1.1. ASD for the receiver
Additive State Decomposition (ASD) is a decomposition method for nonlinear systems just like the superposition principle for linear systems. It aims to decompose a nonlinear system into a linear system (denoted as a primary system) and a nonlinear system (denoted as a secondary system). The basic idea is that the primary linear system describes the dynamics of the original system in the neighborhood of the desired operating point or commanded trajectory, and the secondary nonlinear system is obtained by subtracting the primary system from the original system. The decomposed two systems have the same dimension as the original system. The nonlinearity property is allocated to the secondary system and the tracking task is assigned to the primary system, which makes the controller design more flexible and easier. For general nonlinear time-invariant systems, the ASD procedure is similar to that in the paper27,28. For general nonlinear time-varying systems,the decomposed two systems are a linear time-varying system and a nonlinear time-varying system35. The corresponding ASD procedure is also similar to that in the paper. ASD has been applied in some other applications in our previous papers, and readers can refer to Ref.27,28,35for more details.In the following, ASD is introduced to decompose the aforementioned receiver aircraft model into two subsystems to make the following ILC controller design more flexible and easier.
ASD is applied to system(9).The primary system is chosen as

which is a three-input-three-output linear system. Then, by subtracting the primary system (12) from the original system(9), one has


3.2. Correction algorithm based on adjoint operator
The receiver-related uncertainties can be diminished by controller (23). However, this is not the case for receiver -independent uncertainties. In this part, the receiverindependent uncertainties are considered. Because of the strong nonlinearity of the drogue, the iteration by using the drogue error may not achieve tracking convergence, and is likely to make the receiver oscillate along with the last error,which is unacceptable.Thus, the designed correction term will not iterate. For the integrated system (6), ignoring the nonlinear part, the according operator is defined as Ga.
By utilizing the relative position error of the probe and the drogue at the docking moment,namely-pd/p,k(tdock),a correction term is designed as

where ed/p,k(t )=-pd/p,k(tend) (t ∈[0 ,T]),is the adjoint operator of Ga.
3.3. Controller integration
Finally, by integrating the controller (23) and the correction term Eq.(25), the complete controller is given as

Noteworthy, usr,k+1,Δur,k+1do not iterate, and so the final controller is composed of an iterative feedforward part from the primary system, an online feedback part from the secondary system, and a non-iterative feedforward correction part. The outline of the ILC control scheme used in this work is shown in Fig. 4. The designed iterative learning controller works online. After each docking attempt, the controller adjusts the control input once.
4. Simulation results
In this section,the effectiveness,robustness,and practicality of the proposed control method are demonstrated through simulations and analyses.
4.1. System information
A MATLAB/SIMULINK based simulation environment with a three-dimensional virtual-reality display shown in Fig. 5 has been developed by the authors’ research lab to simulate the docking stage of PDR. The detailed information about the modeling procedure, model parameters, and simulation environment can refer to Ref.29,36.Noteworthy,although the drogue dynamics Eq.(4)is considered in the controller design,the link-connected model of the hose-drogue system is adopted in the simulation environment. A Hose-Drum Unit (HDU) is also included to improve the fitness of the simulation model.
The effect of the system uncertainty and disturbance among different tasks is considered by the following three ways:
(1) Add uncertainties to the actuators by multiplying actuator inputs by a factor of 1.4.
(2) The actual bow wave effect is changed to 1.3 times of the modeled bow wave effect.
(3) Add a side wind disturbance to the atmospheric environment, which primarily acts on the hose-drogue model.
The uncertainty (1) is a receiver-related uncertainty, while uncertainties (2) and (3) are receiver-independent uncertainties.Noteworthy, the aforementioned three changes just apply to the plant,while controller design is still based on the model built previously.
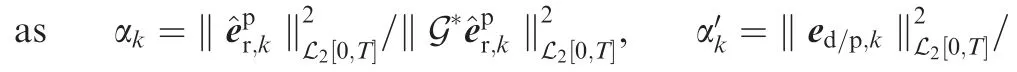

Fig. 4 Controller overview.

4.2. Two existing methods for comparison
As baseline controllers to be compared with, two traditional ILC controllers are briefly introduced. One is a classical Derivative-type (D-type) ILC controller, and the other is an adjoint-type ILC controller, which is similar to the ILC controller for the primary system in this paper.
4.2.1. D-type iterative learning control
A D-type iterative learning controller is designed as

where p=-0.2 is selected.
4.2.2. Adjoint-type iterative learning control
Because the ILC controller for the primary system is similar to the controller designed in Ref.25, the controller in Ref.25is employed for comparison. In this method, the nonlinear system is directly linearized,and then the learning law is designed based on the adjoint operator. Thus, by neglecting the saturation constraint of system (9), one has
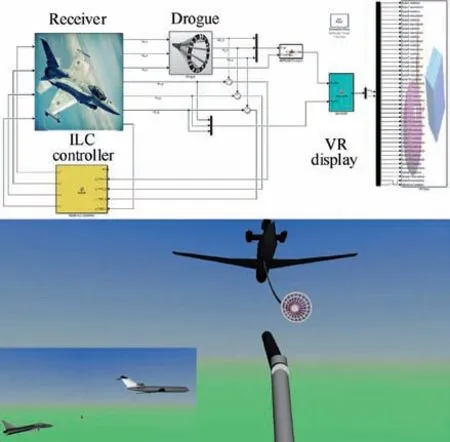
Fig. 5 MATLAB/SIMULINK based simulation environment with a three-dimensional virtual-reality display.
Then, the adjoint-type ILC controller is designed as

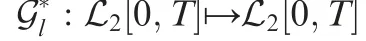
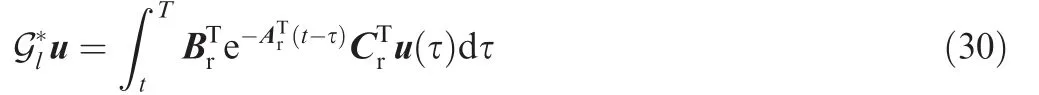
4.3. Simulation results
The convergence of the terminal docking error of different control methods is compared in Fig. 6. Because rd= 0.305 as shown in Fig. 3 (b), a docking attempt is regarded as successful if the docking error edockis less than 0.3. The docking error at the docking moment tdockis summarized in Table 2.Compared with two traditional TILC controllers, the proposed ASDB ILC controller gives the highest convergence speed under uncertainties. Although the classical D-type ILC controller can deal with the NMP systems in theory,its convergence process is extremely slow and unacceptable.The docking error cannot satisfy the precision requirement.In addition,the adjoint-type ILC has a higher convergence speed than that of the D-type ILC. Noteworthy, for the three controllers, the controller parameters are selected carefully. If smaller parameters are selected,the convergence speed will decrease.If larger parameters are selected,the system oscillation will occur.Both of them will lead to worse convergence of the terminal docking error.

Fig. 6 Comparison of the convergence of the terminal docking error of different control methods.
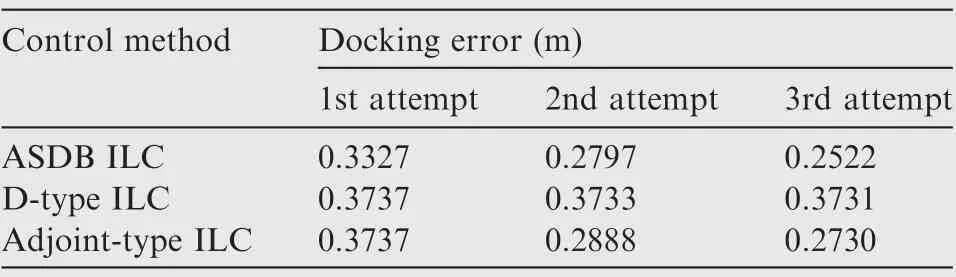
Table 2 Docking errors of different control methods.

Fig. 7 Receiver position during docking process (k=d denotes the reference trajectory).

Fig.8 Relative position and velocity between drogue and probe during docking process.
For ASDB ILC, the receiver position during the docking process is depicted in Fig. 7, and the relative position and relative velocity between the drogue and the probe are shown in Fig.8.It can be observed from Fig.8 that the relative position and relative velocity between the drogue and the probe approach quickly to the reference trajectory, which further reduces the docking error. Noteworthy, the oscillations in Fig. 8 are mainly caused by the drogue, and the oscillation of the receiver is small, which can be verified by Fig. 7. The proposed fast adjustment strategy can deal with various uncertainties and achieve a successful docking in the second docking attempt. The fast adjustment among different tasks can be accomplished.

Fig. 9 Comparison of convergence of terminal docking error with and without turbulence disturbance.
In order to further verify the robustness of the controller,atmospheric turbulence disturbance is taken into consideration by adding the Dryden wind-turbulence model to the PDR system.The designed ASDB ILC controller can still achieve a successful docking in the second docking attempt, as shown in Fig. 9.
5. Conclusions
An additive-state-decomposition-based output feedback iterative learning control method for probe-drogue refueling was introduced. It was shown that ASD could be used to separate NMP feature form input saturation and nonlinearity by dividing the original system into a primary system and a secondary system. Adjoint-type ILC was executed for the LTI primary system,and state feedback was utilized to stabilize the nonlinear secondary system. Furthermore, a non-iterative correction algorithm based on adjoint operator was proposed to compensate for the receiver -independent uncertainties. Simulation results show the promising performance of the ASDB ILC,which outperforms traditional D-type ILC and adjoint-type ILC in the docking control of PDR. ASDB ILC has good tracking effect and high convergence speed under multiple uncertainties. The immediate extension of this work is to integrate it with system identification. Based on the nonlinear model of bow wave effect from system identification, ASDB ILC can achieve better control performance.
Acknowledgement
This work was supported by the National Natural Science Foundation of China (No. 61473012).
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Experimental investigation on operating behaviors of loop heat pipe with thermoelectric cooler under acceleration conditions
- Investigation of hot jet on active control of oblique detonation waves
- Experimental study of rotor blades vibration and noise in multistage high pressure compressor and their relevance
- Unsteady wakes-secondary flow interactions in a high-lift low-pressure turbine cascade
- Effect of protrusion amount on gas ingestion of radial rim seal
- Optimization design of chiral hexagonal honeycombs with prescribed elastic properties under large deformation
