基于图结构特征分析的Top-k结构洞发现算法

朱 江,包崇明,王崇云,周丽华,孔 兵

(云南大学 a.信息学院; b.软件学院; c.生态学与环境学院,昆明 650091)

0 概述

近年来,网络与人们生产生活的关系日益密切,网络数量、规模及数据量均呈现出多元化、复杂化、海量化的发展趋势。在此背景下,如何快速掌握网络关键节点、获取有效信息等成为进一步提高生产生活效率和质量的关键,例如关键节点对网络舆情的控制、社交网络影响力的分析、网络安全薄弱点的发现、信息的快速传播等有重要意义。

结构洞的概念由BURT于2009年提出[1],其对个体在群体之中的关键位置进行深入解释和分析,认为社会结构中处在关键位置的个体将能够获得更多的竞争优势等,但真实网络远比示例网络要复杂得多,随着研究的深入,对结构洞的理解也不再局限于社区间信息流动的关键节点。

结构洞发现算法不断被提出,例如基于社区发现的算法[2-3],该类算法需要预先对社区进行发现和检测,在计算过程和周期上会变得复杂和冗长,同时结构洞的质量取决于社区发现的质量;基于中心性算法和关键性排序算法的优化算法[4](个性化PageRank[5]、中介中心性(Betweenness Centrality,BC)[6-7]、接近中心性(Closeness Centrality,CC)[8-9]等),该类算法能够较快收敛,但精准性相对较弱;此外,还有利用机器学习整合多项数据从而对关键节点排序的算法[10-11]。

本文主要从网络结构方面着手,提出基于最短路径增量与中介中心性过滤的结构洞发现算法(SNV-BC)。SNV算法通过最短路径增量、连通分量个数(Number of Connected Components,NCC)、节点方差(VAR)等数据可精准地区分节点的属性差异,大幅提升算法结果的准确性,但节点属性的精准计算导致了较高的时间成本。由于BC算法与SNV算法在变化趋势上有着较高的一致性和相似度,BC算法计算的是某节点上所通过的最短路径条数,与最短路径增量具有内在一致性,且BC算法时间复杂度极低,因此本文利用BC算法进行节点过滤,并通过SNV算法进行结构洞发现。

1 理论基础

1.1 网络模型定义

节点v的最短路径和c(v)表示以该节点v为起点,到其他所有节点的最短路径长度之和[12]。

(1)

图G的最短路径和c(G)表示图G中所有节点的最短路径长度之和[12]。

(2)

定义1(图最短路径增量) 图中的任何节点都可能在一些节点对间的最短路径上,因此如果移除这样的节点,可能导致该节点对间的最短路径增大甚至不可达(即无穷大)。如果越多的最短路径通过这个节点,那么移除该节点后,各节点的最短路径和势必会增大,图的最短路径也将增加。因此,可以通过图最短路径增量(Shortest Path Increment of Graph,SPIG)来体现节点的重要性。

设G(Vv)表示从图G中移除节点v并将其缩写为Gv,那么SPIG可以表示为:

SPIG(vi)=c(Gvi)-(c(G)-c(vi))⟹

SPIG(vi)=c(Gvi)+c(vi)-c(G)

(3)

对于给定的网络G,c(G)是一个常数。该常数对两个节点之间的SPIG值的比较没有影响。因此,使用SPIG′代替SPIG进行比较,提高计算效率。

SPIG′(vi)=c(Gvi)+c(vi)⟹

SPIG′(vi)=c(Gvi)+c(vi)

(4)

定义2(连通分量个数) 连通分量个数是节点的属性之一,表示移除节点后图中连通分量的数量。通常给定的网络图G是一个连通图,也就意味着NCC(G)=1。然而,移除图G中的节点v可能会形成多个独立的子连通分量。如图1所示,NCC(Gv)=3,缩写为NCC(v)=3,NCC(u)=3,NCC(w)=1。

图1 NCC和节点方差的定义

定义3(节点方差) 节点方差也是节点的属性之一。在移除节点v后,如果形成多个子连通分量,则VAR(v)等于各个子连通分量中节点数量的方差;否则VAR(v)为0。如图1所示,VAR(v)=VAR[|C1|,|C2|,|C3|]=VAR[4,3,4]=0.222,VAR(w)=VAR[|C1|]=VAR[1]=0。

定义4(结构洞属性) 结构洞属性(SH)用于描述节点作为结构洞的可能性大小。SH值越大,其作为结构洞的可能性就越大。

1.2 问题描述与定义

给定网络G=(V,E),结构洞发现就是找到节点集合Vs(Vs⊂V),使得从图G中移除集合Vs中的节点能够导致子图GVs的最短路径增量最大化。换言之,若移除节点v后SPIG值越大,则说明节点v的结构洞属性就越强。

目前,在社交网络的研究中对于结构洞还没有明确的定义,但主要有两个研究方向:一个是重叠社区部分节点[2,13-14];另一个是网络中信息扩散的关键节点[4,15],本文研究更倾向于后者。尽管存在两个研究方向,但相同的是均认为结构洞是一种桥节点。一方面是桥接不同社区,另一方面是信息传播的关键桥梁。如图2所示,3个虚线区域分别表示3个社区,灰色节点直接制约着社区之间以及整个网络的信息流动,因此其被视为具有结构洞属性。

图2 结构洞示意图

定义5(结构洞) 在网络中,桥接不存在直接连接或直连程度较弱的多个社区(或节点群)的中介节点,删除此类桥节点将导致信息扩散成本和时间的增加,甚至信息的不可达。本文将制约网络信息流动的一系列桥节点称为结构洞。

属性1给定节点v和u,节点v桥接多个社区,而节点u仅在社区内连接,根据社区的特性[16],社区内部连通性通常强于社区间的连通性,因此去除节点v对于信息扩散的影响显然要大于去除节点u的影响,v的结构洞属性值也将高于u。

属性2给定节点v和u,节点v桥接多个社区,节点u仅桥接少数几个社区。去除节点v对于信息扩散的影响显然要大于去除节点u的影响,因此v的结构洞属性值也将高于u。

属性3给定节点v和u,节点v桥接两个较大的社区,节点u桥接两个较小的社区或一大一小的社区。对于整个网络的信息扩散而言,移除节点v比移除u的影响更大,因此节点v具有比u更高的结构洞属性值。

属性4在上述3个定义中,如果移除节点后能够形成更多的社区,则说明该节点可以将信息传播到更多的社区,因此更关键。其次是社区中节点的数量,节点的数量越多,信息扩散的范围就越大。因此,一个节点只具有属性2的影响力通常强于只具有属性3的影响力,并强于只具有属性1的影响力。

根据定义1,SPIG的计算依赖于连通图。如果一个节点被移除,可以将整个图分割成多个子连通分量,并且不同连通分量的节点间将是不可达的,因此无法计算得到SPIG值,从而不能获得更有效的SH值。目前,有一部分算法是通过使用极大值来代替无穷远来解决该问题[4]。但如果在图中有更多的节点,或者在删除节点之后产生更多的子连通分量,则极值会被多次迭代计算,这将严重影响计算复杂度和时间复杂度,并且值过大会将一些有用的信息覆盖。因此,本文提出一种基于SPIG、NCC和VAR的结构洞发现算法。

2 SNV-BC结构洞发现算法

2.1 算法原理

本文提出的SNV-BC算法是通过遍历删除每个节点,从而计算每个节点的SPIG、NCC、VAR值,然后分别对这3类值进行归一化并将其合并得到各节点的SH属性值,最终根据该值进行排序得到Top-k结构洞。但在删除节点后如果形成多个连通分量,SPIG值将无法计算,于是通过NCC和VAR来补充数据。本文选择NCC是因为SNV-BC算法不依赖于社区发现,所以使用连通分量个数来代替可能的社区数量。换言之,将移除节点后形成的这些连通分量视为相应数量的独立社区,根据属性2可以得出,如果NCC值越大,那么该节点的SH属性也就越高。

如果一个节点连接着一个叶子节点(度等于1的节点),那么根据上文的思路和定义,移除该节点后这个叶节点也是一个单独的连通分量,同样会被视为一个可能的社区。如图1所示,节点u和叶节点p的关系就属于此情况。这显然是不可行的,将会影响与其他NCC值相同节点的比较,因此提出一个简单的图优化处理办法,其将图中的叶节点全部提前去除。

对于将其分别删除后所形成连通分量数量相等的两个节点,则通过其离心程度来确定其SH属性高低。离心程度通常由eccentricity值来衡量[17],但由于小世界模型的原因[18-19],eccentricity值的区分度非常低,本文提出使用各连通分量中节点数的方差来代替,方差越大说明该节点的离心程度越大,在网络中意味着节点更靠近网络的边缘;反之,节点的方差越小越靠近网络中心,在其他条件相同的情况下,显然靠近网络中心的节点SH属性值应该高于边缘节点。该性质其实就是属性3的体现。如图1所示,分别移除节点u和v,有NCC(u)=NCC(v)=3。对应各连通分量中的节点数,移除节点u为(4,3,4),移除节点v为(2,1,8),进而VAR(u)=0.222,VAR(v)=9.556,VAR(u) < VAR(v),即节点u的SH属性值要强于节点v。可以看出,节点u的位置相对于v要更靠近网络中心,因此对于信息扩散影响和关键性而言,节点u要大于节点v。

在得到这3项重要数据后,为便于综合比较需要将其归并。归并前需要进行归一化处理,NCC和SPIG都是正相关,而VAR是负相关,因此VAR的归一化需要先取其倒数,分别用NCCnorm、VARnorm、SPIGnorm表示其归一化后的数据:

(5)

(6)

(7)

按照式(8)进行合并:

SH(v)=α·NCCnorm(v)+β·(SPIGnorm(v)+

VARnorm(v))

(8)

在式(8)中,SPIGnorm和VARnorm值有且只能存在其中一个,VARnorm是在SPIGnorm无法计算时作为补充,因此将SPIGnorm和VARnorm作为整体统一调整,α、β作为NCCnorm、VARnorm、SPIGnorm的调整参数(0<α<1,0<β<1),其目的是为了控制各成分在最终结果中的比重。

为确定具体参数,本文分别选取(0.2,0.8),(0.4,0.6),(0.5,0.5),(0.6,0.4),(0.8,0.2)5组取值方案进行实验验证。通过最终结果对比发现,α、β取值对于最终排序结果的影响较小,仅对数据差异性存在一定影响。针对本文所用的数据集,α、β分别取0.6、0.4时其区分性较好。对于其他网络数据集,网络中的弱联系越多,不可达情况较高时,α应适当增大;反之,网络的连通性越强且越趋向于强联通时,β应适当增大。

2.2 基于BC算法的过滤原理

由于SNV算法是基于最短路径增量来确定节点的结构洞属性强弱,而最短路径的计算又依赖于对整个数据集节点的遍历,同时由于增量是删除不同节点后不同的差值,因此需要的迭代计算量随着数据集规模的增大呈现出指数级的增加。因此,尝试提前对数据集中的节点进行过滤和筛选处理,从而降低计算量,提高算法效率。根据已有研究和实验,发现SNV算法的准确性相较于BC算法要高很多,但在多数情况下,两算法的变化趋势较为相似和一致。究其原因,SNV算法主要考虑节点删除后最短路径的增量,BC算法主要关注节点上最短路径经过的次数。最短路径经过的次数越多,在删除该节点后,最短路径增量必然也就更大。因此,从内在属性上有着较高的关联性,同时BC算法具有较高的计算效率,利用BC算法进行过滤处理具有理论可能性。需要强调的是,过滤是对下一个需要处理节点的挑选过程,即不再计算被过滤掉的节点的最短路径增量,数据集和图结构仍然保持完整,对于被选择节点最短路径增量的计算没有影响。

Top-k节点的发现算法中节点的排序结果尤为重要和关键。节点排序越靠前代表其作用和价值也越高,同时随着节点排序位置的增加节点价值也随之降低,并且在多数情况和环境下,并不是按线性趋势降低,而是几何级的快速降低。针对本文实验所用数据集大小和需求,将过滤阈值设定为2.5%(即只对前2.5%节点进行计算比较),同时最低不低于50个节点。该阈值可根据不同的需求进行调整。

2.3 算法伪代码

算法1SNV-BC结构洞发现算法

输入无向图G=(V,E)

输出该无向图中每个节点的SH属性值

1.Get Vpassby invoking Procedure 3;

/*通过调用程序3获取被过滤的节点集合*/

2.Let n=|V|n=|V|;

3.For i ← 1 to n do:

4.If vinot in Vpassthen:

/* 只计算未被过滤的节点*/

5.Calculate SPIG,VAR and NCC of viby invoking Procedure 1;

/*通过调用程序1计算SPIG、VAR、NCC */

6.Else

7.SH(vi) ← 0;

8.End if

9.End for

10.For i ← 0 to n do:

/*归一化各节点SPIG,VAR,NCC并求得SH值*/

11.get NCCnorm[vi]NCCnorm[vi]←(NCC(vi)-NCCmin)/(NCCmax-NCCmin) by formula(5);

12.get SPIGnorm[vi] by formula(6);

13.get VARnorm[vi]VARnorm[vi]←(1/VAR(v)-(1/VAR)min)/(1/VAR)max-(1/VAR)min) by formula(7);

14.get SH[vi] by formula(8);

15.End for

16.sort SH

17.Return set SH

程序1计算节点SPIG,VAR,NCC值的伪代码

输入无向图G=(V,E)中的节点v

输出由该节点的NCC,VAR,SPIG组成的字典值vertex_info

1.Let the dictionary data vertex_info ← ∅

2.G.remove (v);/*将节点v从图G中移除*/

3.NCC ← nx.number_connected_components (G);

/*计算连通分量个数*/

4.If NCC==1 then:

5.SPIG′ ← c(Gv) + c(v);

/*通过调用程序2计算相应的c(x)*/

6.VAR ← 0;

7.Else if NCC > 1 then:

8.SPIG’ ← 0;

9.For i←1 to NCC do:

10.NVCC[i]← the number of vertices in each connected component;

/*统计各子连通分量节点数*/

11.VAR ← calculate the variance of NVCC;

/*计算各子连通分量节点数的方差*/

12.Add NCC,VAR and SPIG to vertex_info

13.Return the dictionary vertex_info

程序2计算最短路径c(x)的伪代码

输入无向图G=(V,E)、节点对(v,u)、节点v

输出图的最短路径和c(G)、节点v和u之间的最短路径c(v,u)、节点v的最短路径和c(v)

1.Def BCSP (i,j):

/*通过邻接表计算节点对之间的最短路径 */

2.SP ← shortest_path (i,j);

3.Return SP

4.Def VSP (v):

/*通过调用BCSP计算单源节点的最短路径和 */

5.For i←1 to |V| do:

6.SP ← SP + BCSP (v,i);

7.End for

8.Return SP

9.Def NSP (G):

/*通过调用VSP计算图的最短路径和 */

10.For i←1 to |V| do:

11.SP ← SP + VSP (i);

12.End for

13.Return SP

14.If input is a vertices pair (v,u) then:

/*根据输入类型进行对应计算 */

15.SP ← BCSP (v,u);

16.Elseif input is a vertex v then:

17.SP ← VSP (v);

18.Elseif input is a network G then:

19.SP ← NSP (G);

20.End if

21.Return SP

程序3中介中心性算法过滤筛选的伪代码

输入无向图G=(V,E)

输出优化后被过滤的节点集合Vpass

1.Let n=|V|;

2.k=0.025*n;

/*通过阈值确定选取节点数*/

3.If k<50:

/*将节点数最低值设为50*/

4.k=50;

5.End if

6.Get BC_value=betweenness_centrality(G);

7.sort BC_value;

8.For i ←k to n do:

/*将阈值以后的节点加入到Vpass中*/

9.Add vertex vito set Vpass

10.End for

11.Return set Vpass

2.4 算法时间复杂度

单源节点的最短距离之和c(v)的时间复杂度为O(n),图的最短距离之和c(G)的时间复杂度为n×O(c(v))=n×O(n)=O(n2),因此程序1的时间复杂度为O(n2)+O(n)=O(n2)。整个算法通过过滤筛选,运行时仅需遍历筛选出的50个节点,需要调用50次程序1,因此算法的时间复杂度为50×O(n2)=O(n2),相较于未过滤筛选前的时间复杂度n×O(n2)=O(n3)有显著的提升和改善。

图3为BC算法过滤前后运行耗时情况对比。可以看出,经过优化过滤后,算法耗时减少,同时算法过滤性能较好。

图3 BC算法过滤前后运行时间对比

3 实验结果与分析

3.1 实验环境设定

如表1所示,选取了5个不同类型和规格的网络,包括真实数据网络和人工合成网络,其中Coauthor网络较小。本文预先对结构洞的节点进行人工标注,然后利用NDCG[20]评估方法对各算法的排序结果进行打分,从而评估算法的有效性。人工合成网络使用LFR[21]发生器进行生成。合成网络规模较大,无法人工标注结构洞,也难以进行直观的观察和比较,因此通过SIR[22]模型进行评价和比较。

表1 网络数据集

NDCG是常用的排序结果评价算法。当通过算法得出相应的排序结果后,可以通过NDCG来计算该排序结果相对于标准结果的准确度。NDCG@n表示取前n位排序结果进行准确度计算。

SIR是经典的传染病模型,其中,S(Susceptible)表示易感者,I(Infective)表示感染者,R(Recovered)表示免疫者。易感者与感染者接触后以一定概率α变为感染者,感染者每周期以一定概率β被治愈,并产生免疫力,变为免疫者。后被引入到信息传播研究中。在实验中,将不同算法得到的有序关键节点作为初始感染节点,运用SIR模型在相应网络上进行感染实验,比较网络中的感染范围和感染时间,从而比较和说明算法的优劣。感染范围越大,达到最大感染范围所需时间越短,说明扩散效率越高,节点关键性也越高。

LFR算法由LANCICHINETTI等人于2008年提出[21]。通过该算法能够生成一种标准测试网络。现实网络数据集中的节点度服从幂律分布,利用该算法生成的网络同样服从幂律分布规律和特点,因此利用LFR生成的网络结构来模拟真实网络进行实验。

为评估本文算法,选取了个性化的PageRank算法PersonalRank以及其他基于最短路径的经典算法进行比较:

1)PersonalRank算法[23](为与PageRank区分,记为PPR):其与目前使用较为广泛的个性化PageRank算法最大的差异在于随机游走过程中节点的初始访问概率,PageRank始终以1/N概率运行(N为节点总数)[5],PPR则是根据设定选择相应的根节点开始游走(本文中该算法的根节点选取为网络的中心节点,即离心率最小的节点)。最终通过多轮迭代计算赋予每个节点相应的得分,迭代中随机跳转的参数为0.85,直到得分收敛稳定为止。最终选择Top-k个PPR分值较高的节点。

2)BC算法[6-7]:一个节点担任图中任意两个节点之间SP的桥梁次数或比例。最终选择Top-k个中心性排序较高的节点。

3)CC算法[8]:一个节点到其他节点的最短路径的平均长度。平均路径越小,中心性越高。最终选择Top-k个中心性排序较高的节点。

4)Harmonic接近中心性算法(Harmonic Closeness Centrality,HCC)[9]:其是接近中心性算法的优化算法之一。最终选择Top-k个中心性排序较高的节点。

所有实验均在英特尔(R)酷睿TMI7-6700 3.4 GHz CPU,16 GB RAM,Windows 10企业的操作系统上进行,代码运行平台是Anaconda的Python 2.7。

3.2 算法有效性分析

本文首先对过滤有效性进行实验分析,分别利用SNV-BC和SNV算法对表1中的各数据集进行计算,得到两个不同的节点序列rank_SNV-BC和rank_SNV。其中rank_SNV作为对应基准,再根据NDCG@n(rank_SNV-BC,rank_SNV)进一步计算得到rank_SNV-BC的NDCG评分,从而判断排序的相似情况。

如图4所示,5组评分分别对应表1中各数据集,每组中的5项数据分别代表Top-10、Top-20、Top-30、Top-40、Top-50节点序列的NDCG(rank_SNV-BC,rank_SNV)评分,满分为1,表示过滤前后的节点排序完全相同。从评分情况来看,Coauthor网络数据集的各项均为满分1。LFR-500、LFR-1000、LFR-1500、LFR-2000数据集在过滤前后不同的排序段均保持较高的NDCG评分,说明过滤前后节点序列能够高度吻合,从而进一步说明SNV-BC的过滤算法是有效和可行的。

图4 BC算法过滤前后节点序列的NDCG评分

如图5所示,Coauthor网络是从C-DBLP科研合作网中提取的一个连通子集[10]。为显示数据对比情况,用不同的颜色深度和直径大小表示节点的SH值大小。

图5 Coauthor网络

从图5可以看出,SH值与节点结构关键性的吻合度较高。下文分别采用NDCG@2、NDCG@4、NDCG@6、NDCG@8进一步进行评价。在评价前,需要对网络关键节点进行实际标注,标注的依据为网络中节点所对应作者的真实影响力大小。各算法计算得到的Top-8节点以及人工标记排序的Top-8节点如表2所示,括号中的排序评分用于NDCG计算。

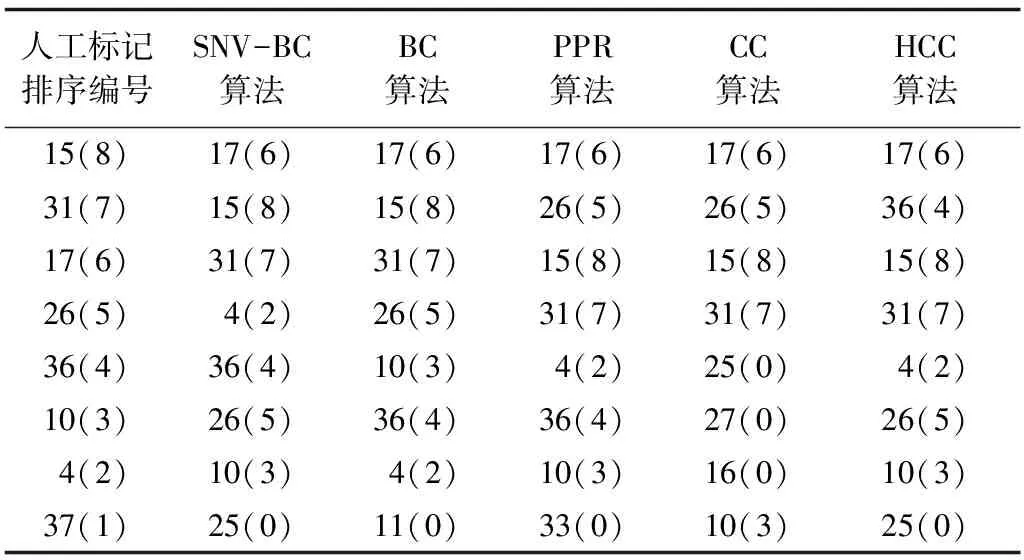
表2 Top-8节点编号(评分)

图6是Coauthor网络的各算法排序的NDCG,分别给出各算法在不同NDCG@n下NDCG评分对比。从图6可以看出,本文提出的SNV-BC算法在该网络中效果明显优于PPR、CC、HCC,仅在部分情况下略低于BC,其主要原因为SNV-BC对于节点4的排序较为靠前,这是由该网络的结构特殊性以及该算法对于子连通分量的过滤较为简单所造成。在移除节点4后,形成{1,2,3},{5,6},{8,9,12,11,13,10,…}3个子连通分量,明显要多于移除节点26,36,10的子连通分量的数量。因此,本文提出的算法对节点4的排序较为靠前。对此进行优化和完善也是后续工作的方向之一,例如加强对子连通分量的过滤。尽管部分情况下效果略低于BC,这主要是网络规模较小、结构较特殊的原因导致,但整体性能表现较好,说明SNV-BC算法是有效可行的。

图6 Coauthor网络NDCG@n评分对比

3.3 人工合成网络上的效果分析

本节首先利用LFR生成多个规模较大的实验网络,然后在不同LFR网络上利用SIR模型进一步对算法效果进行分析。为生成符合要求特性的网络,需要对LFR参数进行相应配置[24],其中,k=6表示平均节点度,max-k=20表示最大节点度,u=0.1表示混合参数,min-c=15表示社区最小节点数,max-c=100表示社区最大节点数。

各算法分别计算求得相应的Top-k节点序列,选取序列中的前n个节点作为SIR模型中的初始传染源进行扩散实验,统一设定SIR模型感染率α为0.8,治愈率β为0.5。由于是概率实验,因此为避免误差影响,每一种情况下都进行50次计算并将其平均值作为最终结果。

图7(a)、图8(a)、图9(a)、图10(a)分别是LFR-500、LFR-1000、LFR-1500、LFR-2000网络数据集上各算法结果的感染率对比。可以看出,随着初始感染节点数量的增加,本文提出SNV-BC算法的感染率均呈现出稳定的增长趋势。在LFR-500、LFR-1000和LFR-1500网络上多数情况下要明显优于其他算法。在LFR-2000网络中,部分区间其他算法的感染率高于SNV-BC算法,但是波动较大,而SNV-BC算法仍然保持较为稳定的增长趋势。

需要注意的是,尽管整体呈现出增长的趋势,但各网络数据集中的算法均不同程度的存在部分区间的最大感染率反而随着初始感染节点的增加而降低的情况,如图8(a)中SNV算法的初始传播源节点数为15～20,图9(a)中PageRank算法的初始传播源节点数为3～6。这是由网络结构和SIR模型中免疫节点的免疫隔离共同作用的结果。免疫感染率降低程度越大,说明隔离程度也越明显,从一定程度上反映了节点的关键性越强。在社交网络分析研究中,可以理解为人们对于同一信息的兴趣(或者信息的传播扩散能力),随着该信息被接收次数的增加会快速降低甚至忽略。如果关键节点免疫越早,其隔离作用也就生效的越早,其对于整个网络的信息扩散隔离效果就越明显。

从一定程度上来看,各算法感染率的区分度还不是很明显。因此,本文通过比较达到最大感染率所需的时间来进一步说明本文提出算法的优势。图7(b)、图8(b)、图9(b)、图10(b)分别是LFR-500、LFR-1000、LFR-1500、LFR-2000网络数据集上各算法达到最大感染率所需时间的对比。可以看出,本文提出的SNV-BC算法达到最大感染率所需时间较短,并且随着初始节点数量的增多,均提早多个周期达到最大感染率,进而表明所得到的Top-k节点关键性更强,充分体现了算法的有效性。从最大感染率和达到最大感染率所需时间曲线图中也可以看出,SNV算法和SNV-BC算法变化趋势基本保持一致,进一步证明BC算法过滤的有效性和可行性。

图7 LFR-500网络中6种算法效果对比

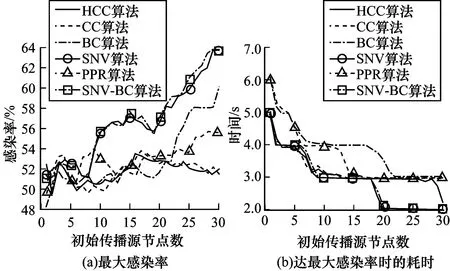
图8 LFR-1000网络中6种算法效果对比

图9 LFR-1500网络中6种算法效果对比

图10 LFR-2000网络中6种算法效果对比

4 结束语

本文分析并研究了复杂网络上Top-k结构洞的问题,提出基于最短路径增量与中介中心性过滤的结构洞发现算法SNV-BC,利用NDCG评估方法和SIR模型在多个网络上对SNV-BC算法进行评估。实验结果表明,该算法可以更准确地找到结构洞,同时利用中介中心性算法提前完成过滤筛选,有效控制和降低算法的时间复杂度。后续将对节点过滤算法进行优化,进一步提高结构洞发现算法效率。