基于二阶时序差分误差的双网络DQN算法

陈建平,周 鑫,傅启明,高 振,付保川,吴宏杰

(苏州科技大学 a.电子与信息工程学院; b.江苏省建筑智慧节能重点实验室,江苏 苏州 215009)

0 概述

强化学习(Reinforcement Learning,RL)是一种通过与环境交互将状态映射到动作以获取最大累积奖赏值的方法[1]。该方法设计思想来源于条件反射理论和动物学习理论,是一类重要的机器学习算法。自20世纪80年代被提出以来,经过不断发展,强化学习已经在工程设计、模式识别、图像处理、网络优化等方面得到了广泛应用[2]。由于强化学习方法特有的学习和计算方式,其在解决一些大规模或连续的状态空间任务时,状态空间的大小随着特征数量的增加而呈指数级增长趋势,所需计算量和存储空间也指数级增长,导致“维数灾难”[3]问题,因此,传统的强化学习方法无法满足大状态空间或者连续状态空间的任务需求。目前,解决“维数灾难”问题的主要方法是状态抽象和函数逼近。其中,函数逼近可以有效减少状态的存储空间,并且在大规模数据的训练中具备一定的泛化特性。

在解决大规模状态空间的强化学习问题时引入深度学习(Deep Learning,DL)[4-5]可实现复杂函数的逼近。深度学习的概念源于对人工神经网络的研究,其通过学习一种深层的非线性网络结构,拟合数据与标签之间的非线性关系,从而学习数据的本质特征[6],实现复杂函数的逼近。谷歌的DeepMind团队在此基础上创新性地将具有决策能力的强化学习与具有感知能力的深度学习相结合,提出了深度强化学习(Deep Reinforcement Learning,DRL)[7]的概念。此后,DeepMind构造了人类专家级别的Agent,其对自身知识的构建与学习都来源于原始输入信号,无需任何人工编码和领域知识,充分体现了DRL是一种端到端的感知与控制系统,具有很强的通用性[8]。此后,深度强化学习被广泛应用于各种问题,如AlphaGo[9]、对抗网络架构[10]、机器人控制[11-12]等。

在深度强化学习概念出现之前,研究者主要将神经网络用于复杂高维数据的降维,以便于处理强化学习问题。文献[13]结合浅层神经网络与强化学习解决视觉信号输入问题,控制机器人完成推箱子等任务。文献[14]提出视觉动作学习的概念,将高效的深度自动编码器应用于视觉学习控制中,使智能体具有与人相似的感知和决策能力。文献[15]通过结合神经演化方法与强化学习,在赛车游戏TORCS中实现了赛车的自动驾驶。文献[16]将深度置信网络引入到强化学习中,用深度置信网络替代传统的值函数逼近器,成功应用于车牌图像的字符分割任务。文献[17]采用Q学习构建误差函数,利用深度神经网络优化蜂窝系统的传输速率。文献[18]将卷积神经网络与传统RL中的Q学习[19]算法相结合,构建深度Q网络(Deep Q-Network,DQN)模型用于处理视觉感知的控制任务。此后,DeepMind团队结合DQN模型与目标Q网络模型对原始的DQN模型进行改进,进一步提升其处理视觉感知任务的能力[20]。文献[21]提出基于时序差分(Temporal Difference,TD)误差自适应校正的DQN主动采样方法,估计样本池中样本的真实优先级,提高了算法的学习速度。

本文针对原始DQN算法因过估计导致稳定性差的问题,提出一种基于二阶TD误差的双网络DQN算法(Second-order TD-based Double Deep Q-learning Network,STDE-DDQN)。通过构造2个相同的DQN结构协同更新网络参数,并且基于二阶TD误差重构损失函数,从而增强学习过程中值函数估计的稳定性。

1 相关理论

1.1 马尔科夫决策过程

马尔科夫决策过程(Markov Decision Process,MDP)可以用来解决序贯决策问题,而强化学习任务是一个典型的贯序决策过程。因此,利用马尔科夫决策过程对强化学习问题进行建模,可以有效解决强化学习任务。

在强化学习中,通过估计动作值函数可以衡量Agent在某一策略π下动作选择的优劣程度,其中,优劣程度根据可以利用的未来累积奖赏进行评估。策略π是指在状态s下采取动作a的概率,可以表示为π(s,a)。动作值函数Qπ的定义如式(1)所示:

Qπ(s,a)=Eπ{Rt|st=s,at=a}=

(1)

其中,γ是折扣率,决定着未来奖赏的当前价值。如果当前策略是最优策略,则所对应的动作值函数即为最优动作值函数Q*,定义如式(2)所示:

(2)

1.2 时序差分学习

时序差分(TD)学习结合了蒙特卡洛和动态规划思想,能够从原始的经验中学习,是一种模型无关的强化学习方法。

TD方法对状态值函数进行评估,可以利用经验样本解决预测问题。通过判断学习过程中行为策略与目标策略是否一致,可以将TD学习分为两类:在策略学习与离策略学习。Q学习算法是一种经典的离策略算法,行为策略一般使用ε-greedy策略。此外,基于Q学习对动作值函数进行评估,可以用于解决控制问题。Q学习中的Q值函数更新公式如式(3)所示:

Q(st,at)←Q(st,at)+β[rt+1+

(3)

其中,β是学习率,rt+1是立即奖赏,γ是折扣率。在这种情况下,学到的动作值函数Q直接逼近最优动作值函数Q*,且不依赖于其行为策略。

1.3 DQN算法

DQN算法将深度学习与强化学习相结合,直接从高维的输入学习控制策略,实现“端到端”的学习。该算法模型利用神经网络逼近动作值函数,通过经验回放解决数据相关性及非静态分布问题,并使用目标网络解决模型稳定性问题。相较于其他模型,DQN具有较强的通用性,可用于解决不同类型的问题。

在DQN算法中包含两个相同的网络:目标网络和估值网络。初始化时,两个网络的权值相同。在训练过程中,对估值网络进行训练更新,通过直接赋值的方式对目标网络进行权值更新。

在每一次的迭代更新过程中,从经验池中随机抽取小批量样本(st,at,rt,at+1),将st输入估值网络,输出在状态st下每一个动作的Q值,即估值网络的预测值Q(st,at)。在训练过程中,通过求解标签值对估值网络进行权值更新。在计算标签值时,将st+1输入目标网络,输出在st+1状态下每个动作对应的最大Q值,即Q*(st+1,at+1),使得累积折扣奖赏最大。同时,每训练N步,则将估值网络的权值赋值给目标网络,进行一次更新。

DQN模型通过Q学习中的TD误差构造如下损失函数:

(4)

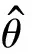
然而,利用式(4)求解损失函数时,目标网络Q值的迭代过程采用max操作。由式(5)可知,对Q值进行max操作后,其比优先计算目标Q值期望后进行max操作的值大。因此,在原始DQN算法中,利用目标网络最大Q值替代目标网络Q值期望值的计算,会导致目标Q值的计算存在过估计,从而造成算法收敛性能的不稳定。

E(max(Q1,Q2))≥max(E(Q1),E(Q2))

(5)

2 基于二阶TD误差的双网络DQN算法

在原始DQN模型中,目标Q值的计算存在过估计,会导致损失函数的计算出现偏差,降低算法收敛稳定性。针对该问题,本文提出一种基于二阶TD误差的双网络DQN算法。在DQN模型的基础上增加一个相同的值函数网络,并提出二阶TD误差的概念,构建二阶TD误差模型与新的损失函数更新公式。通过两轮值函数的学习,降低目标Q值最大化的影响,克服单一目标Q值计算存在过估计的问题,有效减小模型的计算误差,提高算法中值函数估计的稳定性。

2.1 双网络DQN模型

针对DQN算法由于过估计导致收敛性差的问题,结合TD误差阶的定义,在DQN的基础上增加一个相同的值函数网络模型,从而提高算法的收敛性能,改进后的结构模型如图1所示。

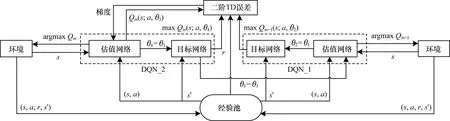
图1 基于二阶TD误差的双网络DQN模型结构

在图1中,为保证二阶TD误差双网络结构的稳定性,设置DQN_1与DQN_2结构中的初始化权重参数θ相同。在二阶TD模型中,DQN_2的估值网络与环境交互,将得到的数据存入经验池,同时自动更新参数,将估值网络中的参数传递给DQN_1中的估值网络。在DQN_2与环境第1轮交互后,DQN_1与环境交互,Agent进行第2轮的学习。

在第2轮学习结束后,Agent在前两轮学习的基础上,通过DQN_1目标网络中的动作值函数与DQN_2结构中估值网络和目标网络中的动作值函数,构建新的损失函数,利用梯度下降对权重进行求解,以逼近真实目标Q值。之后,在DQN_2上进行第3轮学习,直至所有的情节结束。此外,每间隔N步,DQN_1与DQN_2模型中的估值网络都会将权重参数复制给各自的目标网络。

2.2 二阶TD误差

在任意第m次迭代计算中,任意时刻t,当前状态动作对为(st,at),Q学习以前一轮对(st,at)的估计差值作为TD误差,如式(6)所示:

TDEm(st,at)=βt[rt+1(st,at)+

γmaxQm-1(st+1,at+1)-Qm-1(st,at)]

(6)

其中,TDEm(st,at)是在第m轮中t时刻状态动作对的TD误差,βt是学习率,rt+1(st,at)是该状态动作对的立即奖赏值,γ是折扣率,Qm-1(st+1,at+1)是m-1轮中t+1时刻的状态动作对的估值,Qm-1(st,at)是m-1轮中t时刻的状态动作对的估值。在式(6)中,当前状态动作值的估值是基于后续状态动作对估值的最大值,即利用后续状态动作对的Q值的极值,代替状态动作对的真实极值,进而计算TD误差。

定义1(N阶TD误差) 在第m轮,任意时刻t,立即奖赏为rt+1,记Q值为:

Qm(st,at)=rt+1+γmaxQm(st+1,at+1)

(7)

其中,Qm(st+1,at+1)是第m轮对t+1时刻状态动作对的估值。N阶TD误差的定义如式(8)所示,记为TDE(n),并且n≥1,n为阶数。当n为2时,称为二阶TD误差,记为TDE(2),如式(9)所示:

(1-αm){αm[Qm-n(st,at)-Qm-1(st,at)]+

(8)

(1-αm)[Qm-1(st,at)-Qm-2(st,at)]

(9)

2.3 损失函数构建

算法的实际输出与期望输出差值越大,即损失函数的值越大,算法的收敛效果越差。本文针对算法收敛稳定性问题,构造两个相同的DQN结构,引入二阶TD误差的概念重构新的损失函数,达到提升算法收敛性能的目的。

在DQN模型的学习过程中,从经验池随机选择样本数据,通过梯度下降的方式进行参数更新。在二阶TD误差双网络DQN结构中,利用经验回放进行随机采样,通过二阶TD误差函数进行学习,并更新权重参数θ。二阶TD误差计算公式如式(10)所示:

(α-1)[Qm-1(st,at;θ4)-Qm-2(st,at;θ2)]

(10)

其中,θ2为DQN_1模型目标网络的参数,θ3与θ4分别为DQN_2模型中估值网络和目标网络的参数。在模型训练的每一步参数更新过程如下:将DQN_2中估值网络的参数传递给DQN_1中的估值网络,且同时保持自身的更新,即θ3=θ1,θ3=θ3,其中θ3表示DQN_2中估值网络下一状态的权重参数,每间隔N步,将DQN_1中的估值网络参数传递给目标网络,即θ2=θ1,同时将DQN_2中的估值网络参数传递给目标网络,即θ4=θ3。

由此得到改进后的损失函数如式(11)所示:

L(θ)=Es,a,r,s′{[(1-α)(TQ2-TQ1)-

α(TQ1-BQ2)]2}

(11)

其中,损失函数是两个网络参数值的方差,并受参数α的影响,网络结构的目标值与估计值也取决于网络权重参数。在训练时,要保持当前目标网络权重参数的固定,防止算法收敛不稳定。对损失函数式(11)求解权重导数,得到权重梯度如式(12)所示:

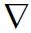
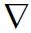
(12)

2.4 STDE-DDQN算法

根据上文介绍,给出基于二阶TD误差双网络DQN算法流程,如算法1所示。

算法1基于二阶TD误差的双网络DQN算法

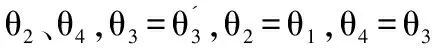
2.For episode=1,M do

3.初始化状态s1;

4.For t=1,T do

5.采用ε-greedy策略选择动作;

6.得到执行动作at后的奖励r,以及下一时刻的状态st+1;

7.将数据(st,at,rt,st+1)存入到D中;

8.随机从D中取出样本(st,at,rt,st+1)进行训练;

9.判断状态是否为中止状态,若是则目标为rT,否则计算目标值;

10.利用式(11)计算损失函数;

11.利用式(12)更新权重参数θ1与θ3;

12.每N步迭代后,θ2=θ1,θ4=θ3;

13.End for

14.End for

3 实验与结果分析

3.1 Mountain Car问题求解

3.1.1 实验描述

为验证本文算法的性能,将本文提出的基于二阶TD误差双网络DQN算法与原始DQN算法应用于经典控制Mountain Car问题进行比较。

Mountain Car问题示意图如图2所示,其中一辆车在一维轨道上,位于两座“山”之间,即带有坡面的谷底,目标是把车开到右边的山上(图2中小旗的位置)。然而,小车由于动力不足,不能一次通过山体,因此小车必须借助前后加速的惯性才能通过山顶。Mountain Car实验的状态是两维的,其中一维表示位置,另一维表示速度。其中,小车的位置区间为[-1.2,0.6],速度的区间为[-0.07,0.07]。动作空间有3个离散动作,分别表示向左、向右、无动作。在情节开始时,给定小车一个随机的位置和速度,然后在模拟环境中进行学习。当小车到达目标位置(图2中小旗的位置)时,情节结束,并开始一个新的情节。

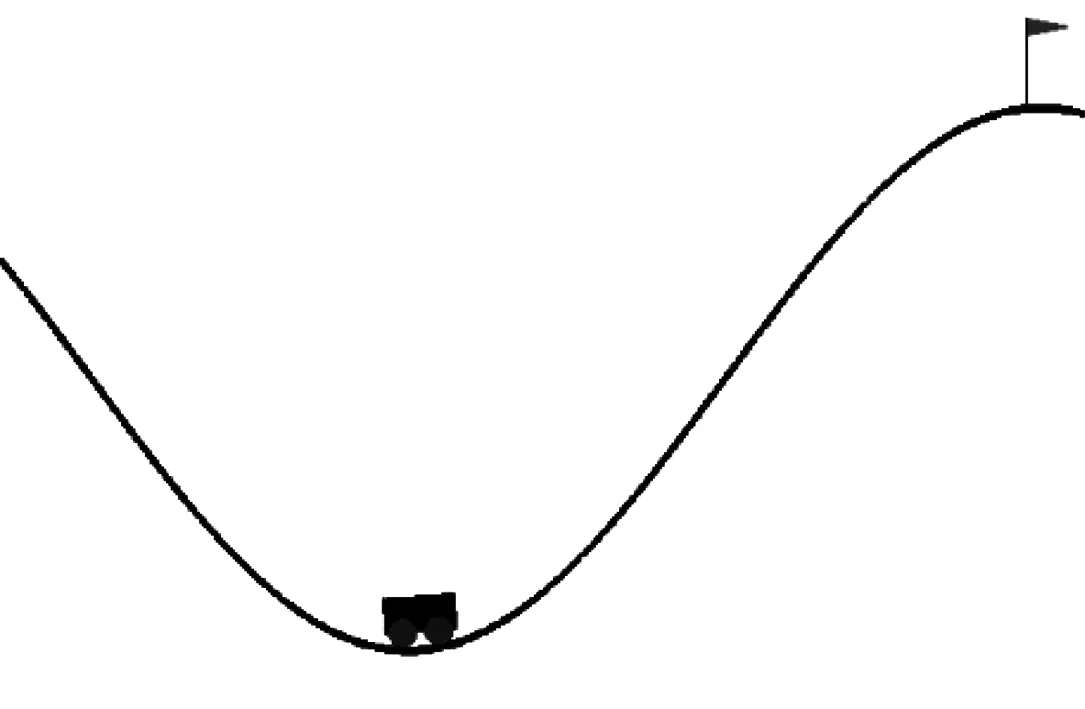
图2 Mountain Car问题示意图

当小车到达目标位置时,立即奖赏是1,其他情况下立即奖赏与位置有关。奖赏函数如式(13)所示:

(13)

3.1.2 实验设置

本文的实验环境是Open AI Gym,神经网络参数的优化器是RMSprop,隐藏层使用的线性修正单元为ReLU。

实验中的具体参数设置为:学习率β为0.001,ε-greedy策略中ε的值为0.9,其迭代的速率为0.000 2,迭代间隔为300,经验池的数量为3 000,情节数量设置为500,训练中mini-batch的值为32。

3.1.3 实验分析

在α不同取值情况下,比较二阶TD误差双网络DQN算法和传统DQN算法应用于Mountain Car问题的性能表现,如图3所示(每个实验执行500个独立情节)。其中,α分别取值0.1、0.3、0.5和0.7。在实验过程中,每个算法都被独立执行20次,求出平均值。

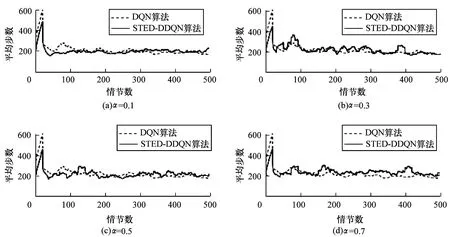
图3 2种算法求解Mountain Car问题的性能对比

从图3(a)可以看出,α取0.1时,在第40个情节处的平均步数降至最低,之后缓慢收敛至稳定值,第70个情节后稳定在200步左右。从图3(b)可以看出,α取值为0.3时,算法在前400个情节的实验过程中都有大幅度的振荡,效果较差,第400个情节之后的性能与DQN算法性能相似。从图3(c)可以看出,α取值为0.5时,二阶TD误差双网络DQN算法的实验效果与DQN算法的收敛效果相似,符合上文的理论推导。从图3(d)可以看出,当α取值为0.7时,算法的实验效果在500个情节内有3个明显的振荡高峰,收敛效果变差。由此看出,α取值逐渐变大时,振荡幅度变大,算法的收敛性能越差。这是由于双网络DQN算法在TD误差的基础上引入了二阶TD的概念,使得算法能够在两个同构值函数网络的学习基础上进行新一轮的迭代学习,减小了算法模型的计算误差,进一步提高了算法的收敛稳定性。因此,二阶TD误差双网络DQN算法的前期收敛速度比DQN更快,振荡较少且更接近收敛值。综上,当α取值为0.1时,算法的收敛效果最好。

图4是在α=0.1的条件下,选取不同学习率β的算法效果对比。可以看出:β取0.001时,算法前20个情节学习的效果与其他取值情况相似,第20个～第70个情节时学习效果较好,第100个情节处有一个较大幅度的振荡,第240个～第270个情节处有较高幅度的振荡,之后算法逐渐稳定至收敛值;β取0.002时,前期学习效果较差,第50个～第120个情节时有较大幅度的振荡,第120个～第500个情节时都有较小幅度的振荡;β取0.005时,算法在第50个情节～第100个情节处有较小幅度的振荡,之后的情节中有小幅度的振荡,相比其他取值情况,收敛效果较好。因此,根据实验结果与实验分析,学习率β的值选择0.005效果最好。由此看出,面对离散动作问题时,学习率并非越小越好,学习率的选择需要根据具体问题分析。

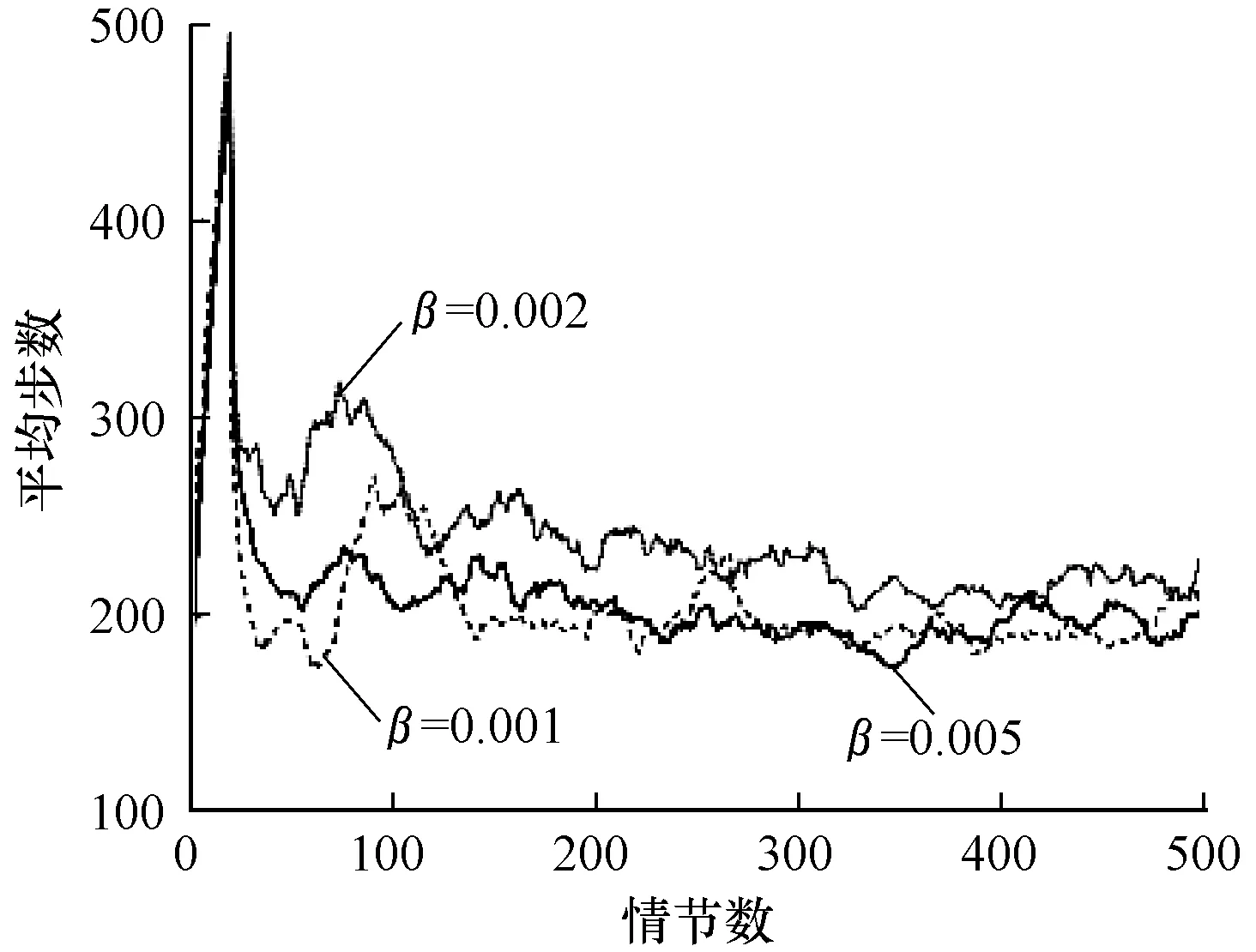
图4 不同β取值下本文算法的学习性能

Fig.4 Learning performance of the proposed algorithm under differentβvalues

在学习率β取0.005且α=0.1的情况下,针对不同ε-greedy最大取值对学习效果的影响进行对比,如图5所示,其中,ε的最大值分别取0.90、0.95以及0.99,且每次动作选择后,每一次的迭代值为0.000 2。可以看出:ε最大值取0.90时,算法前期逐步收敛,收敛效果相比其他取值较好,第400个～第460个情节处有轻微振荡;ε最大值取0.95时,算法前期振荡明显,第160个情节之后逐渐稳定至收敛值;ε最大值取0.99时,算法在前150个情节振荡幅度巨大,之后的情节中振荡幅度逐渐降低。原因是算法的前期需要积极探索更有效的策略,当ε取值较大时,前期每个情节探索最优动作的概率较大,经过多个情节,ε的值就会降低到最小,导致前100个情节震荡幅度较大,难以收敛。因此,综合上述分析,ε取值为0.9时效果最好。

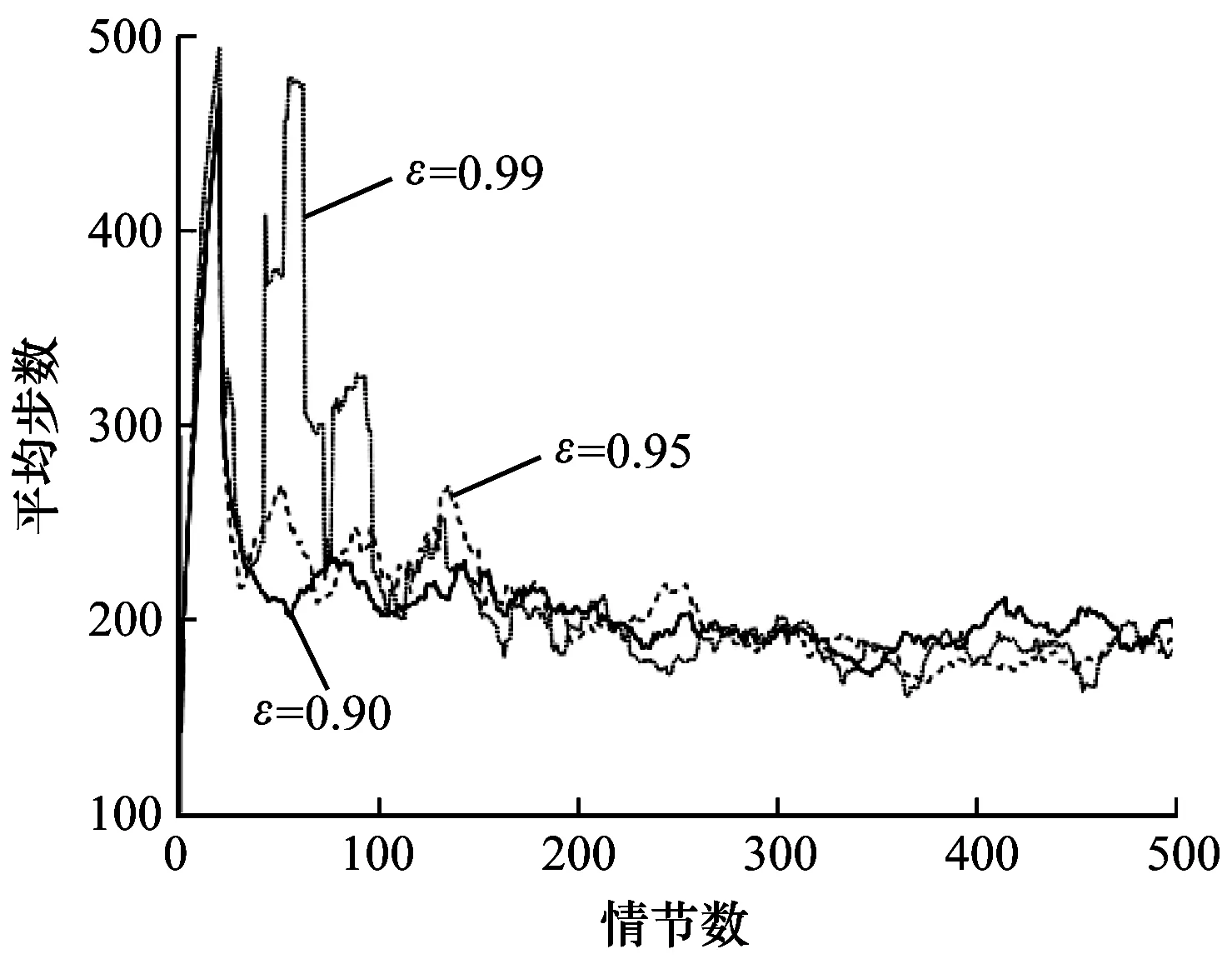
图5 不同ε取值下本文算法求解Mountain Car问题的性能

Fig.5 Performance of solving Mountain Car problem by the proposed algorithm under differentεvalues

3.2 Cart Pole问题求解

3.2.1 实验描述

为进一步验证二阶TD误差双网络DQN算法的性能,将其与原始DQN算法应用于空间状态更为复杂的平衡杆(Cart Pole)问题进行性能比较。

Cart Pole问题示意图如图6所示,其中一根杆由一个非驱动的接头连接到一辆小车上,小车沿着无摩擦的轨道运行。

图6 Cart Pole问题示意图

该系统的状态是四维的,可以表示为:Ssate={x,xdot,T,Tdot};动作是一维的,有2个离散动作:向左或向右。系统中通过施加一个+1或-1的力来控制小车,且当钟摆处于直立状态时,Agent的目标是阻止它倒下。当Agent控制操作杆走一步,且杆子保持垂直时,环境给予Agent一个立即奖赏,当杆子与垂直方向的角度超过15°,或者小车从中心移动超过2.4个单位时,游戏结束。为使奖赏函数更合理有效,设置奖赏函数如式(14)所示:

(14)

3.2.2 实验设置

本文的实验环境是Open AI Gym,神经网络参数的优化器是RMSprop,隐藏层使用的线性修正单元为ReLU。

实验中的具体参数设置为:学习率β为0.01,ε-greedy策略中ε的值为0.9,ε迭代的速率为0.001,迭代间隔N为100,经验池的数量为2 000,情节数量设置为3 000,训练中mini-batch的值为32。

3.2.3 实验分析

在α不同取值情况下,比较二阶TD误差双网络DQN算法和传统DQN算法应用于经典Cart Pole问题的性能表现,如图7所示(实验中每个算法都独立执行3 000个情节)。针对α的取值设计实验,验证算法的收敛性能与α值设置的关联性,其中,α分别取值0.1、0.3、0.5和0.7。

图7 2种算法求解Cart Pole问题的性能对比

从图7可以看出,原始DQN算法约在第60个情节处开始学习,到750个情节时趋于稳定值400,在之后的情节中仍有较高幅度的振荡,并且算法在第2 000个情节左右获得最低奖赏值。从图7(a)可以看出,α取0.1时,二阶TD误差双网络DQN算法也在60个情节左右开始学习,在第250个情节处接近稳定值500,之后的情节中有轻微振荡,第1 800个～第2 000个情节时有较大波动,最终能够稳定收敛并且取得比DQN算法更高的奖赏值。从图7(b)可以看出,α取0.3时,二阶TD误差双网络DQN算法在第250个～第1 700个情节性能表现较好,之后的情节中振荡较大,收敛性能较差。从图7(c)可以看出,α取0.5时,算法的收敛性能与DQN算法相似,满足上文的理论推导。从图7(d)可以看出,α取0.7时,算法的振荡幅度较大,没有明显的收敛表现。通过对比分析可以得出结论:当α取0.1时,算法的收敛效果最好,稳定性最强。比较不同取值情况下α的取值可知,STDE-DDQN算法由于引入二阶TD误差,其通过相同值函数网络的迭代学习可降低模型的学习误差,具有更好的收敛稳定性。

图8是二阶TD误差双网络DQN算法在α取0.1时不同学习率下的收敛效果对比,其中分别设置学习率β为0.01、0.005以及0.002。可以看出:β取0.01时,在第250个情节时开始收敛,收敛稳定值为520,第1 750个～第2 000个情节处收敛性能下降,之后在收敛值附近振荡,且振荡幅度较大;β取0.005时,与其他取值情况相比,前期收敛较慢,且在收敛值左右振荡,从第300个情节处开始,一直在收敛值左右轻微振荡,整体性能表现较好;β取0.002时,算法学习率较低,学习缓慢,但初期学习效果较好,第200个情节处开始收敛,在第2 000个～3 000个情节处算法的振荡幅度较大,收敛效果较差。由此可知:当学习率较大时,算法收敛较快,但振荡幅度较大,容易陷入局部最优的问题,难以收敛;当学习率较小时,学习效果较好,但算法学习速率较慢,收敛情况不稳定。因此,综合上述分析,学习率β的值选择为0.005时,算法的性能最好。

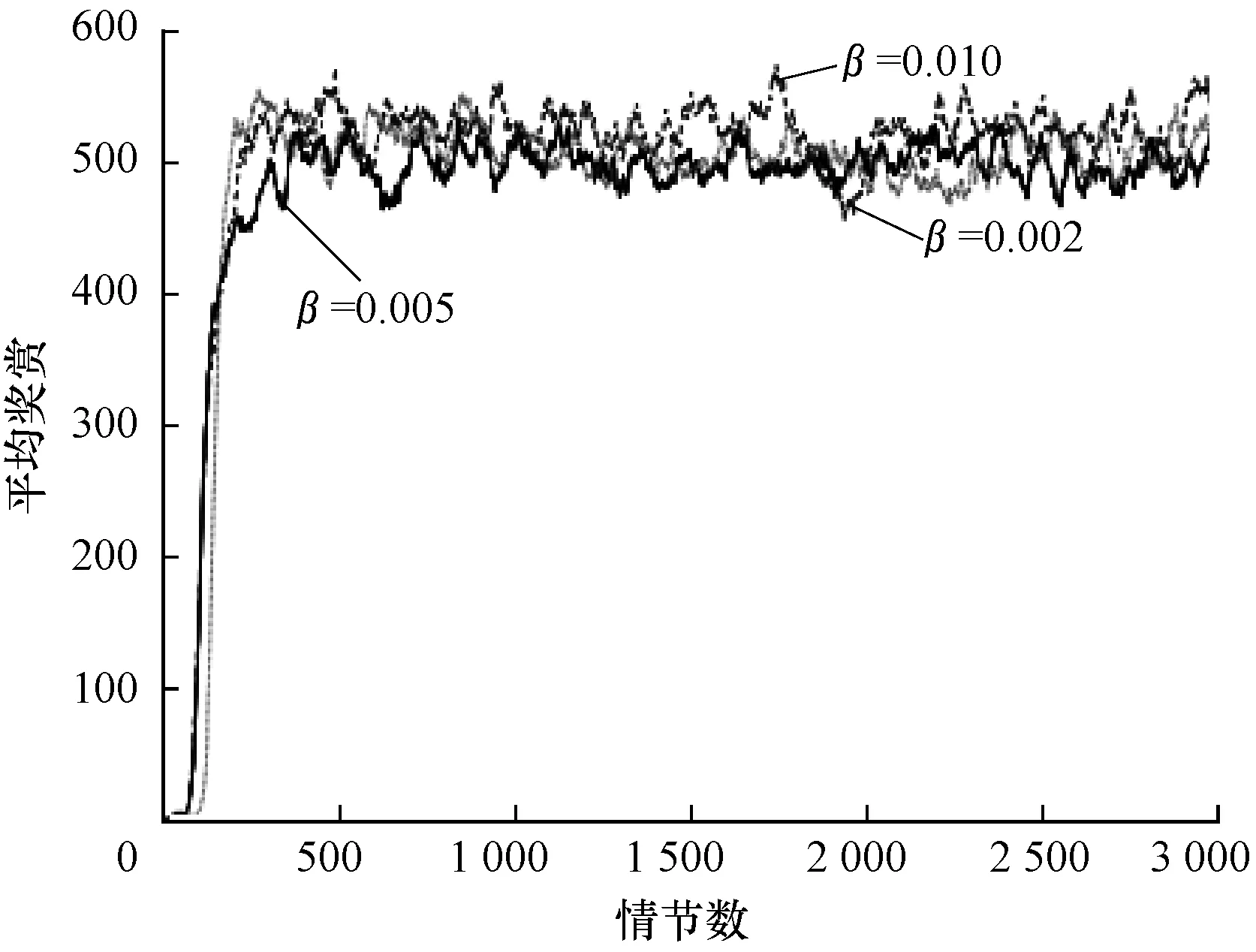
图8 不同β取值下本文算法求解Cart Pole问题的性能

Fig.8 Performance of solving Cart Pole problem by the proposed algorithm under differentβvalues

图9是在保证α与学习率β的情况下,选取不同ε-greedy策略二阶TD误差双网络DQN算法的收敛效果对比。可以看出:ε取0.90时,算法收敛较慢,在第400个情节处开始收敛,并在之后的情节中一直以较小的振荡幅度维持在收敛稳定值左右;ε取0.95时,算法在第300个情节处开始收敛,且收敛速度较快,振荡幅度较小;ε取0.99时,算法的平均奖赏较高,达到650左右,但是算法不易收敛,振荡幅度较大,原因是ε-greedy策略取值较大,前期Agent探索概率大,易找到最优策略与最优值,但后期动作选择时,ε的值过小,缺少探索,不易收敛。因此,ε取值为0.95时效果最好。

图9 不同ε取值下本文算法求解Cart Pole问题的性能

Fig.9 Performance of solving Cart Pole problem by the proposed algorithm under differentεvalues

4 结束语

本文通过引入N阶TD误差的概念,提出一种基于二阶TD误差的双网络DQN算法。构建两个同构的值函数网络分别表示先后两轮的值函数,并重构损失函数,使Agent能够在先后两轮值函数的基础上进行学习,减小学习误差,提高算法的收敛稳定性。此外,还通过对比实验探索收敛效果更好的参数取值。基于Gym实验平台的Mountain Car和Cart Pole求解实验结果表明,该算法能够有效提高值函数估计的稳定性,具有较好的收敛性能。本文工作通过引入二阶TD误差设计改进的DQN算法,下一步将针对更高阶的情况对算法收敛性能进行优化。